Table 2.

Research paper characteristics related to the free convection heat transfer.

Ref	Geometry Description	Nanofluid	Methodology	Results	Decision Variables
[15]	Inclined, porous, semi-annulus enclosure	Magnetic Fe3O4 -water	Free convection, Buongiorno and Darcy models, FVM, SIMPLE	- Adding nanoparticle volume fraction → Nu increases - Increase in porosity number → Nu increases	10 ≤ Ra ≤ 1000 Porosity number = 0.4, 0.7 0 ≤ $\phi$ ≤ 0.04 0 ≤ inclination angle of cavity ≤ 90
[16]	Square enclosure and convection around a circular cylinder, different geometries of cylinders	Ag-water	Free convection, Darcy–Brinkman model	- Porous layer thickness increases (20% to 80%) → free convection performance decreases (up to 50%)	103 < Ra < 106 10−5 < Da < 10−1 0% < thickness of porous layer < 100% 1 < thermal conductivity ratio 0 < $\phi$ < 0.1
[17]	Square enclosure	MWCNT–Fe3O4/water	Free convective MHD, MRT, Lattice–Boltzmann	- Increase in Ra → increase in heat transfer rate - Increase in Ha → decrease in Ra - Increase in Nu (+4.9%)	10−2 < Da < 10−1; 103 < Ra < 105; 0.4 < porosity < 0.9; 0 < $\phi$ < 0.003; 0 < Ha < 50;
[18]	Inclined square enclosure and exothermic chemical reaction administered by Arrhenius kinetics	Tilted nanofluid	Free convective Buongiorno nanofluid model, FEM	- Re increases → Nu decreases	Dissemination of streamlines; isotherms; iso-concentrations; and average Nusselt number
[19]	Square cavity and linearly heated left wall with composite nanofluid–porous layers	Cu-water	Free convection, Galerkin finite element method, Darcy–Brinkmann model	- Increase in Ra → intense streamlines	$\phi$ = 0.1; 10−7 ≤ Da ≤ 1; 103 ≤ Ra ≤ 107
[20]	Inverse T-shaped cavity	MWCNT–Fe3O4/water	Free convection MHD, extended Darcy–Brinkman–Forchheimer model	- Lower inclination angle → higher Nu - Lower values of ratio of dimensionless convection coefficient and the magnetic field viscosity parameter → significant heat transfer enhancement	0 ≤ magnetic field viscosity parameter ≤ 1; 0.7 ≤ porosity ratio ≤ 1.4; 0 ≤ magnetic field inclination angle ≤ $\pi ;$ 0 ≤ ratio of dimensionless convection coefficient ≤ 10; Ha = 20; Ra = 105
[21]	Square cavity and two semicircular heat sources in the wall	MWCNT–Fe3O4/water	Free convection, FEM	- Ra = 1 × 104 → Nu increases with magnetic number	100 < Magnetic number < 5000; 0.2 < Strength ratio of magnetic sources < 5; 0 < Ha < 50; 0.1 < porosity coefficient < 9
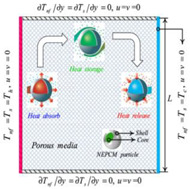
[22]		Nano-Encapsulated Phase Change Materials (NEPCM)	Free convection. local thermal non-equilibrium (LTNE)	- Increase in thermal conductivity of porous medium → and increase in heat transfer	0 ≤ $\phi$ ≤ 0.05
[23]	Transient natural convection and a square cavity, considering nanoparticle sedimentation	Al2O3/water	Free convection	- Nu decreased - Reduction in convection heat transfer	104 < Ra < 107; 10−5 < Da < 10−2
[24]	Square cavity	Ag–MgO/water	Free convection, LTNE, Darcy model, Galerkin FEM	- Increase in Ra→ increase in the vortex’s strength - Increase in heat transfer (5.85 times)	10 ≤ Ra ≤ 1000; 0.1 ≤ ε≤0.9; 0 ≤ φ ≤ 0.02; 1 ≤ H ≤ 1000
[25]	Inclined enclosure with wavy walls and partially layered porous medium	Cu-Al2O3 water	Free convection, Galerkin FEM, Darcy–Brinkman model	- Increase in heat transfer	0 < inclination angle < 90; 104 ≤ Ra ≤ 107; 10−2 ≤ Da ≤ 10−5; 0.2 ≤ porous layer width ≤ 0.8; 1 ≤ number of undulations ≤ 4; 0 ≤ $\phi$ ≤ 0.2
[26]	Eccentricity heat source and porous annulus	Cu-water	Free convection	- Increase in heat transfer	0 ≤ ϕ ≤ 0.04; 103 ≤ Ra ≤ 106; 10−4 ≤ Da ≤ 10−1;
[27]	Transient natural convection and non-Darcy porous cavity with an inner solid body	Al2O3 -Water	Free convection, Buongiorno model, Brinkman–Forchheimer extended Darcy formulation. FDM	- Higher Da→ uniform nanoparticle distribution - Increasing porosity → uniform nanoparticle distribution - Maximum Nu enhancement is approximately 30%	The porosity of the porous medium; Darcy number; The nanoparticles’ average volume fraction
[28]	Inner corrugated cylinders inside wavy enclosure and porous–nanofluid layers	Ag nanofluid	Free convection	- Increase in Ra and Da → increase in fluid flow strength and shear layer thickness - Increase in porous layer thickness→ decrease in heat transfer	106 ≥ Ra ≥ 103; 0.1 ≥ Da ≥ 0.00001; 0.2 ≥ vertical location (H) ≥ −0.2; 6 ≥ number of sinusoidal inners; cylinders (N) ≥ 3
[29]	Inverse T-shaped cavity and trapezoidal heat source in the wall	Fe3O4- water	Free convection, magnetic field dependent (MFD), FEM	- Local and average Nu increased	Darcy, Hartmann, and Rayleigh numbers; inclination angle; cavity aspect ratio
[30]	Spherical electronic device	Cu-water	Free convection, SIMPLE algorithm	- Heat transfer increases - Average Nu increases	6.5 × 106 < Ra < 1.32 × 109; 0 < $\phi$ < 10%; 0 < thermal conductivity of the porous material’s matrix < 40
[31]	Tilted hemispherical enclosure	Water-ZnO	Free convection experiment	Increase in heat transfer	0 < inclination angle < 90; 0 < $\phi$ < 8.22%
[32]	Wavy-walled porous cavity and inner solid cylinder	Al2O3/water	Free convection, FEM, Forchheimer–Brinkman extended Darcy model, Boussinesq approximation	- Higher values of Da → heat transfer enhancement	0 ≤ $\phi$ ≤ 0.04; 10−6 < Da < 10−2; 0.2 ≤ ε ≤ 0.8
[33]	Partitioned porous cavity for application in solar power plants	MWCNT–Fe3O4/water	Free convection, CFD method, volume averaging the microscopic equations	- Increase in Da, Ra → Nuave increases	103 < Ra < 106; 0.5< porosity coefficient ratio < 1.8; 0 < $\phi$ < 0.003; 0.1 < Ri < 20; 0.01 < Da < 100; Thermal conductivity ratio = 0.2, 0.4, 1, 5
[34]	Square cavity and inner sinusoidal vertical interface	Ag/water	Free convection, Galerkin FEM	- Increase in Da, Pr → Nuave increases	0.6 < power law index < 1.4; 10−5 < Da < 10−1; 0 < $\phi$ < 0.2; 1 < undulation number (N) < 4; 0.015 < Pr < 13.4; Ra = 105
[35]	Hot rectangular cylinder and cold circular cylinder	copper–water	Free convection, Brinkman-extended Darcy model, Brinkman correlation	- Heat transfer enhanced	Rayleigh number; Hartmann number; Darcy number; magnetic field inclination angle; nanoparticles volume fraction; nanoparticles shape factor; nanoparticles material; nanofluid thermal conductivity; dynamic viscosity models; nanofluid electrical conductivity correlation on streamlines; isotherms; local and average Nusselt numbers
[36]	Partially heated enclosure	Al2O3/water	Free convection, FEM, Brinkman equation	- Heat transfer rate augmented - Ra, Da increases → average velocity	103 < Ra < 106; 0 < $\phi$ < 5%; 0 < Ha < 100; 0.001 < Da < 1
[37]	I -shaped cavity	Cu–water	Free convection, MHD, FDM	- Ha increases → Nu decreases - Ra increases → Nu increases - Maximum Nu occurs at B = 0.2 - Minimum Nu occurs at B = 0.8	Ha; nanofluid volume fraction; heat source size; location and angle of magnetic field on heat transfer; entropy generation; thermal performance
[38]	Porous enclosure	Cu, Al2O3 and TiO2/water	Free convection, MHD	- Increase in magnetic field intensity→ heat transfer deterioration - Enlarging nanoparticles, denser nanoparticles→ heat transfer deterioration	0 ≤ Ha ≤ 50; Nanoparticle volume fraction; Nanoparticle diameter
[39]	Inclined cavity	Al2O3- water	Free convection Entropy generation	- Increase in chamber angle → increase in heat transfer - Adding nanoparticle volume fraction → increase in heat transfer	Rayleigh number Hartmann number; magnetic field angle changes; chamber angle changes; entropy parameter; radiation parameter; volume percent of nanoparticles
[40]	Cubical electronic component and hemispherical cavity	Water-ZnO	Free convection, control volume method	- Inclination increases → Nuava decreases - Nanofluid concentration increases → heat transfer increases	0 < volume fraction < 10%; Nuave
[41]	Inverted T-shape	MWCNT–Fe3O4/water	Free convection, thermal transmission	- Ha increases → Nuave decreases	Heat transfer performance; flow structures
[42]	Inverse T-shaped cavity and trapezoidal heat source in wall with wavy Wall	Magnetic Al2O3/water	Free convection, FEM, Koo–Kleinstreuer–Li (KKL) correlations	- Increase in Ra, decrease in Ha → increase in flow intensity -	Heat generation parameter; the shape factor of nanoparticles; Hartmann number; nanoparticle concentration; displacement of the trapezoidal heater wall; Rayleigh number; the amplitude of wavy wall