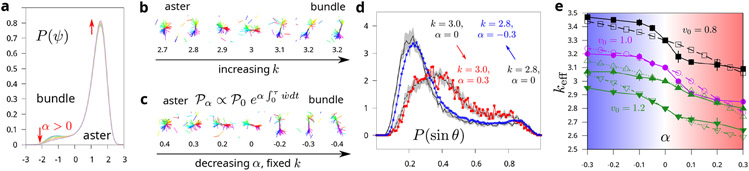
FIG. 2.

Dynamical bias effectively renormalizes the motor rigidity k. (a) Probability distribution obtained by biasing the dynamics of a given order parameter ψ (with free energy $ℱ(\psi )=-a\psi +b{\psi }^2-c{\psi }^3+d{\psi }^4$) with respect to ψ. Parameters: a = 4d = −b = −30c = 1. Biasing parameter: α = 0 (unbiased dynamics, blue), 0.005 (green), 0.1 (orange) and 0.3 (purple). (b) Snapshots of unbiased simulations with changing motor rigidity k. (c) Snapshots of simulations from biased simulations with fixed motor rigidity k = 3. (d) The statistics of structure from biased dynamics matches with that from an unbiased simulations at a different k. The order parameter sin θ is calculated from angles between neighboring filaments and averaged across nearest neighbors. Matching the distribution of sin θ from biased (black lines with the error bar shown with gray area) and unbiased simulations (red and blue) results in defining an effective rigidity k_eff. (e) Effective rigidity k_eff as a function of bias parameter α at v₀ = 0.8 (black), 1.0 (magenta), and 1.2 (green). The two green curves correspond to k = 3 and 2.8 analyzed for v₀ = 1.2. Filled points are obtained by matching structures from biased and unbiased simulations. Hollow points are analytical predictions derived from the two-state model (Eq. (7)).