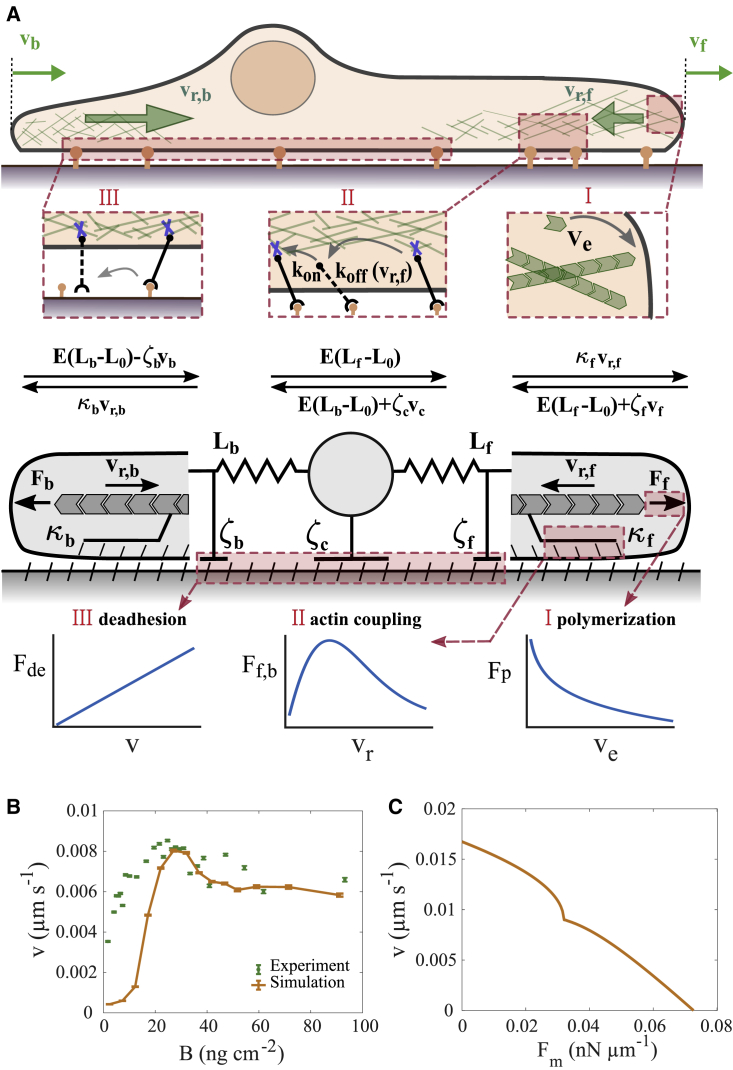
Figure 2.

(A) Model constituents. Cartoon of a cell moving on a 1D fibronectin lane (top), force balances (middle), and the mechanical components of the model (bottom). Front and back protrusion edges move with velocities $v_f$ and $v_b$, respectively. The F-actin networks flow with the retrograde flow rates $v_{r,f}$ and $v_{r,b}$, respectively. The forces $F_b={\kappa }_b{v}_{r,b}$ and $F_f={\kappa }_f{v}_{r,f}$ arise from polymerization of F-actin, act on the protrusion edge membrane, and drive retrograde flow against the friction forces. The front and back edge membrane experience drag with the coefficients ${\zeta }_f$ and ${\zeta }_b$, respectively. Elastic forces $E\left(L_f-L_0\right)$ and $E\left(L_b-L_0\right)$ act between the cell body and the edges (equilibrium length $L_0$). The balance of the elastic forces determines the motion of the cell body against the drag force ${\zeta }_c{v}_c$. Bottom panels illustrate types of essential relations of the model. The de-attachment force of the back $F_{de}$ is linearly related to velocity. The friction force between F-actin network retrograde flow $v_r$ and stationary structures exhibits a maximum in its dependency on retrograde flow (clutch). The polymerization force $F_p$ is logarithmically related to the network extension rate $v_e$ due to the force dependency of the polymerization rate. (B and C) Two constitutive relations. (B) The adhesion-velocity relation. Green dots represent experimental data (see Table S1 and Data S7). Error bars represent the standard error of the mean. (C) The stationary force-velocity relation predicted by the model for $B$ = 45 ng cm⁻² (see section S10 for details). It provides the cell velocity under constant application of the external force $F_m$ to the leading edge or cell body. Parameter set 1 from Table S2 is used for both panels. To see this figure in color, go online.