Abstract
Localization of anatomical landmarks is essential for clinical diagnosis, treatment planning, and research. This paper proposes a novel deep network named feature aggregation and refinement network (FARNet) for automatically detecting anatomical landmarks. FARNet employs an encoder-decoder structure architecture. To alleviate the problem of limited training data in the medical domain, we adopt a backbone network pre-trained on natural images as the encoder. The decoder includes a multi-scale feature aggregation module for multi-scale feature fusion and a feature refinement module for high-resolution heatmap regression. Coarse-to-fine supervisions are applied to the two modules to facilitate end-to-end training. We further propose a novel loss function named Exponential Weighted Center loss for accurate heatmap regression, which focuses on the losses from the pixels near landmarks and suppresses the ones from far away. We evaluate FARNet on three publicly available anatomical landmark detection datasets, including cephalometric, hand, and spine radiographs. Our network achieves state-of-the-art performances on all three datasets. Code is available at https://github.com/JuvenileInWind/FARNet.
Keywords: Anatomical landmark detection, Deep network, Feature aggregation, Feature refinement, Exponential weighted center loss
Introduction
Anatomical landmark localization is a prerequisite not only for patient diagnosis and treatment planning [1–4], but also for numerous medical image analysis tasks including image registration [5, 6] and image segmentation [7]. In practice, manually or semi-automatically locating landmarks is tedious, time-consuming, and prone to errors. Therefore, there is a strong need for fully automatic and accurate landmark localization approaches. But identifying anatomical landmarks is challenging because of the variations in individual structures, appearance ambiguity, and image complexity. Anatomical landmark localization has been applied to 2D and 3D medical image modalities. The examples of 2D modality include cephalometric and hand radiographs, and the examples of 3D modality include 3D brain MR scans, 3D olfactory MR scans, and 3D prostate CT images. In this paper, we focus on 2D anatomical landmark localization.
In recent decades, numerous automatic anatomical landmark detection methods have been proposed. Rule-based methods [8, 9] utilize image processing techniques to detect edges/contours and identify the landmarks based on prior knowledge of the landmark structures. However, rules would become too complex to formulate with increasing image complexity. Some works adopt template matching [9–11] to locate landmarks. To consider both the local appearance and the global spatial configuration of landmarks, some works [12–15] employ the Active Shape Model and Active Appearance Model. Later, machine learning algorithms, such as neural networks, SVM, and random forest, have been applied to landmark localization for better generalization in case of anatomical variation and noise. These methods formulate landmark localization as a classification problem or a regression problem. Classification-based methods [16–20] determine whether a landmark is located in an image patch. Regression-based methods [6, 7, 21–28] predict the displacement from an image patch to a certain landmark. Some machine learning–based approaches [7, 18, 20, 24–26, 28] further combine the local predictions with global configuration modeling to improve the detection accuracy.
Deep learning has achieved great success in many fields, such as computer vision and natural language processing. It has also been applied to medical image analysis, including anatomical landmark detection. However, the limited medical training data makes it challenging to train deep networks for anatomical landmark detection. To alleviate this problem, some deep learning–based landmark detection methods perform patch-wise regression/classification [29–31]. However, it is time-consuming for these methods to train and test on many image patches. In addition, patch-based methods only utilize local information and ignore global information, making them unable to predict all landmarks accurately. Recently, a few end-to-end CNN-based methods have been proposed for landmark detection, which utilizes an entire image as input and facilitates the modeling of global information. Some of these methods [32, 33] directly regress the landmark coordinates, and others [32, 34–38] adopt fully convolutional networks (FCN) to regress heatmaps, each of which encodes the pseudo-probability of a landmark at a specific pixel position. However, due to the limited training data, very shallow networks are adopted in these methods and limit their capacities. In addition, the previous networks’ output resolutions usually have a stride of 4 or are even smaller, further introducing quantization errors to the predictions. Therefore, there is a need for developing deep networks with high-resolution feature extraction for accurate anatomic landmark detection.
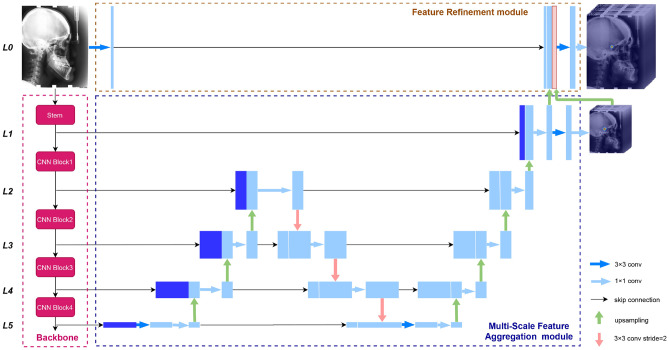
This paper proposes a novel end-to-end deep network, FARNet (shown in Fig. 2), for anatomic landmark detection. FARNet employs an encoder-decoder structure architecture. To alleviate the problem of limited training data, we adopt a backbone network pre-trained on natural images as the encoder. The decoder includes a multi-scale feature aggregation (MSFA) module and a feature refinement (FR) module. The MSFA module combines multi-scale features extracted by the backbone with up-sampling and down-sampling paths and skip connections. Features with different resolutions are combined by concatenation in a higher-resolution-dominate manner. The elaborate design of the MSFA module achieves a good trade-off between the network capacity and efficiency. To achieve high-resolution prediction, we propose the FR module that combines the feature maps extracted from the input image with the up-sampled feature maps and heatmaps from the MSFA module to generate feature maps with the exact resolution as the input image. Coarse-to-fine supervisions are also applied to the two modules to facilitate end-to-end training. To achieve accurate heatmap regression, we propose a novel loss function named Exponential Weighted Center loss, which focuses on the errors from the pixels near landmarks and suppresses the losses from far away. FARNet is evaluated on three publicly available datasets in the medical domain (examples are shown in Fig. 1): the cephalometric radiograph dataset [4], the hand radiograph dataset [37], and the spinal anterior-posterior X-ray dataset [33]. Our network achieves state-of-the-art performances on all these datasets, proving our network’s effectiveness and generality.
Fig. 2.
The architecture of the feature aggregation and refinement network (FARNet). FARNet includes a backbone network (in the pink dashed box), a multi-scale feature aggregation (MSFA) module (in the blue dashed box), and a feature refinement (FR) module (in the brown dashed box). We also give the feature level labels at the left side of the figure, and all feature maps at the same horizontal level have the same spatial resolution
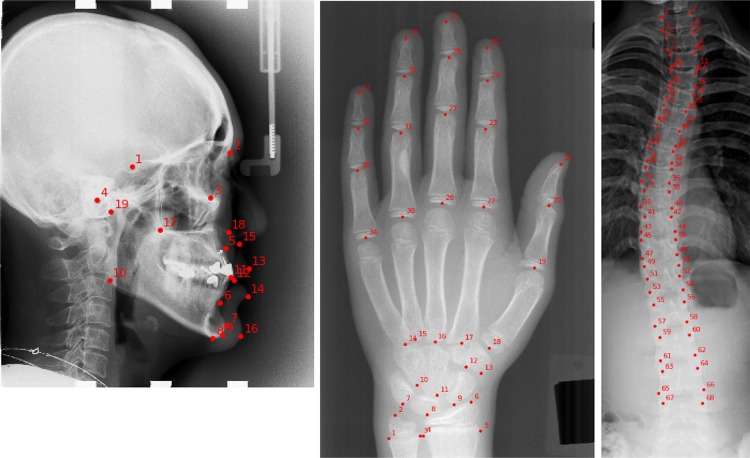
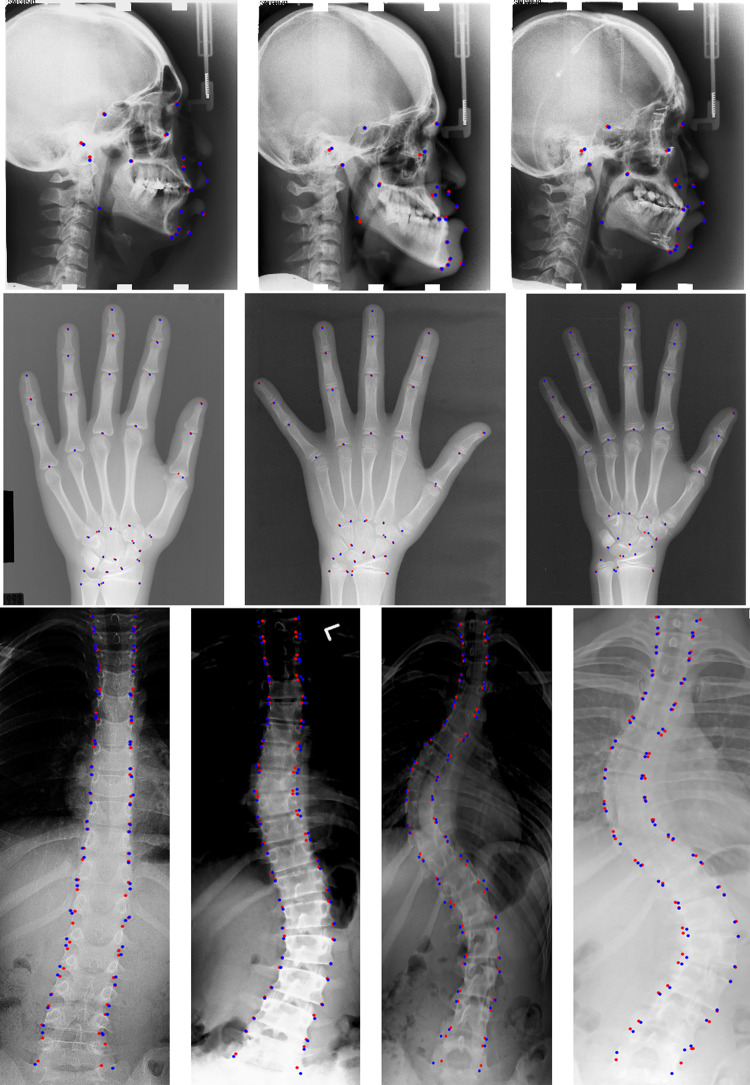
Fig. 1.
Sample images and the anatomical landmarks for three datasets used in this paper. From left to right are lateral cephalogram with 19 landmarks, radiograph of left hand with 37 landmarks, and spinal anterior-posterior X-ray with 68 landmarks
Our contributions are summarized as follows,
We propose a novel deep network with encoder-decoder architecture for anatomic landmark detection, which can fuse multi-scale features from the encoder and achieve high-resolution heatmap regression.
We compare several widely used pre-trained networks as the encoder of our network, and DenseNet-121 achieves the best performance.
To achieve more accurate localization, we propose a novel loss function named Exponential Weighted Center loss for heatmap regression.
Experimental results indicate that our network achieves state-of-the-art performances on three public medical datasets.
The rest of this paper is organized as follows. The “Related Work” section presents a brief review of the related works. Our proposed network and loss function are described in the “Proposed Method” section. The “Experiments and Results” section reports the experimental setups and results on three public medical datasets. Finally, the discussion and conclusion are give in the “Discussion” section and “Conclusion” section respectively.
Related Work
Deep Learning Methods for Anatomical Landmark Detection
Deep learning has achieved great success in many computer vision applications and has also been applied to anatomic landmark detection. One of the main challenges to deep learning–based anatomical landmark detection is the limited medical imaging data for network training. Some methods perform patch-wise regression/classification to alleviate this problem. But the patch-based approach is time-consuming and unable to capture global information, which is also crucial for accurate prediction. For 2D landmark detection, another solution to the limited training data problem is to use the backbone networks pre-trained on natural images. Furthermore, different methods have been proposed to incorporate global context with local information to improve landmark prediction. For example, some methods combine patch-based CNN predictions with a statistical shape model; some adopt CNNs with encoder-decoder structure; others learn global context and local features in order or in different network branches.
Aubert et al. [30] utilized a deep neural network to predict the displacement from an input image patch to an anatomical landmark and employed a statistical shape model (SSM) to regularize the whole detection process. Arik et al. [31] trained a CNN on small patches to output probabilistic estimations of landmarks and refined the positions of landmarks by a shape-based model. Xu et al. [39] leveraged an FCN to estimate an action map (up, down, left, or right) and localized landmarks based on the estimated action map by a robust aggregation approach. Lee et al. [32] trained 38 independent CNNs to regress the coordinates of the 19 cephalometric landmarks separately, and their method is very time-consuming for training and testing. Wu et al. [33] extended a CNN with a robust feature embedding layer to remove outlier features and a structured multi-output regression layer to regress landmark coordinates.
However, direct regression of the coordinates from images involves a highly nonlinear mapping, which has been noticed by research works for human pose estimation [40, 41]. Therefore, many landmark detection methods regress heatmaps, each of which encodes the pseudo-probability of a landmark located at a specific pixel position. Payer et al. [35] used CNN to regress the heatmap of each landmark and used another network to combine the local feature of each landmark with its spatial relations to all other landmarks to improve the prediction accuracy. O’Neil et al. [36] trained an FCN with low-resolution images to learn spatial context, trained another FCN with higher resolution images, and learned spatial information for further refinement. Payer et al. [37] combined U-Net and their SpatialConfigurationNet by multiplying their output heatmap predictions for accurate and robust landmark detection. Zhong et al. [38] proposed two-stage U-Nets for landmark detection. A global U-Net takes an entire image as input and regresses the heatmaps of landmarks in low resolution. Guided by the coarse attention from the global stage, a local stage with patch-based U-Net regresses heatmaps in high resolution. Chen et al. [42] proposed an attentive feature pyramid fusion module to fuse features from different levels of a pre-trained network, then combined predicted heatmaps and offset maps to perform pixel-wise regression voting to improve detection accuracy. DACFL [43] forces the CNN to learn richer representations by perturbing the local appearance of training images based on prior anatomical distribution and adopts the Anatomical Context loss to help learn the anatomical context based on spatial relationships between the landmarks.
Some works transfer landmark detection to other tasks, such as objection detection and image segmentation. For example, Qian et al. [44] detected landmarks by Faster R-CNN with a multi-task loss function and used a two-stage repair strategy to remove the abnormal candidate landmarks. Liu et al. [45] converted landmark detection to segmentation of the landmark’s local neighborhood and solved it with a U-Net-based approach which employs a non-local module with pyramid sampling to capture the global structural features.
To alleviate the problem of limited training data, we utilize a backbone network pre-trained on nature images whose feature extraction capacity is more potent than the shallow U-Net-based networks. The work [42] also uses a pre-trained network to extract multi-scale features and enhances the fused features with attention to improve the prediction accuracy. However, the main drawback of this work is that the number of its attention-enhanced feature maps is linear to the number of landmarks which significantly increases the number of parameters, memory storage, and computational cost.
Multi-scale Feature Fusion
By aggregating features at multiple resolutions, multi-scale feature fusion can combine local information with context to improve feature discriminability. In the last a few years, some multi-scale feature aggregation networks have been proposed for object detection [46, 47], image segmentation [48–50], and human pose estimation [51, 52]. Among them, the encoder-decoder structure is widely used. An encoder module contains a down-sampling convolution path to extract the semantic and context information from an input image, and a decoder module has an up-sampling convolution path to recover spatial information of features. Skip connections are often added from encoder layers to the corresponding decoder layers with the same resolution to preserve spatial information at each resolution. Some encoder-decoder networks, such as U-Net [49] and Hourglass [51], are shallow networks that limit their capacities. A solution to this is to stack multiple such networks as in [51], but it remarkably increases the number of parameters and model size. Other networks, such as FCN [48], FPN [46], DeepLab [50], and the simple baseline network [52], use pre-trained networks like VGG [53] and ResNet [54] as their encoders for feature extraction, and an up-sampling path as a decoder to combine multi-scale features. PANet [47] adds an extra down-sampling feature aggregation path on top of FPN to enhance the entire feature hierarchy with accurate localization signals. Tan et al. [55] proposed BiFPN, which treats each bidirectional (up-sampling and down-sampling) path as a feature network layer and repeats it multiple times to enable more high-level feature fusion. In the work [42] for cephalometric landmark detection, lateral connections and up-sampling are used to fuse features from different levels of the backbone network.
Inspired by FPN and its variations, we propose a MSFA module. For the network capacity and efficiency trade-off, we construct the MSFA module with one bidirectional (up-sampling and down-sampling) path followed by an up-sampling path. The MSFA module has one more down-sampling and up-sampling path than FPN and is more effective. Compared to PANet and BiFPN, the MSFA has one more up-sampling path to support higher-resolution prediction. The MSFA module is more efficient than BiFPN with repeated bidirectional paths.
Loss Functions for Keypoint Detection
Besides medical landmark detection, keypoint detection has other applications, such as facial landmark detection and human pose estimation. In [56], Feng et al. demonstrated that the L1 and smooth L1 loss functions performed much better than the L2 loss for coordinate regression–based facial landmark detection and proposed the wing loss to improve the accuracy of facial landmark detection further. Recently, heatmap regression has become the mainstream approach to keypoint detection tasks, and the Mean Square Error (MSE) loss, also known as loss, is the commonly used loss function. However, the wing loss does not apply to heatmap regression due to its high sensitivity to small errors on background pixels and the discontinuity of gradient at zero. The Adaptive Wing loss [57] updates it for heatmap regression to focus more on loss from foreground pixels than background pixels. The drawback of the Adaptive Wing loss is that it has four hyper-parameters to tune.
This paper proposes a more straightforward and effective loss function with only one hyper-parameter for heatmap regression. We update the MSE loss by multiplying a factor to focus more on errors at the pixels near landmarks than from far away. Our experiments indicate the new loss function is more effective than the Adaptive Wing loss and other loss functions for anatomic landmark detection.
Proposed Method
Feature Aggregation and Refinement Network
The architecture of our FARNet is shown in Fig. 2, which employs the encoder-decoder structure architecture. To alleviate the problem of limited training data in the medical domain, we utilize a backbone network of DenseNet [58] pre-trained on ImageNet [59] as the encoder, which extracts feature maps at multiple scales. The decoder includes a MSFA module and a feature refinement (FR) module. The MSFA module consists of up-sampling, down-sampling feature aggregation paths, and lateral connections to fuse multi-scale features extracted by the backbone. The FR module generates high-resolution feature maps for landmark prediction.
FPN [46] uses the feature maps output by the last residual block of convolution stages 2, 3, 4, and 5 of ResNet and denotes them as which have strides of pixels with respect to the input image. The stem block of ResNet includes a convolutional layer with stride 2 followed by a max-pooling layer with stride 2. Following FPN, we denote the feature maps output from the convolutional layer of the stem block as C1, which has a stride of 2. For convenience, we denote the feature levels of a CNN as which have strides of , respectively.
For high-resolution prediction, the MSFA module combines feature maps from C1 to C5. And our FR module further combines feature maps with the same resolution as the input image, denoted as C0. Note that FPN and PANet combine features from C2 to C5, and BiFPN fuses features from C3 to C7 of EfficientNets. Compared to them, our network generates higher-resolution feature maps, which is helpful for accurate landmark detection. More details about the MSFA module and FR module are given in the following.
Multi-scale Feature Aggregation Module
The practice of FPN, PANet, and BiFPN demonstrates the effectiveness of the up-sampling and down-sampling feature fusion paths, and the more paths, the better fusion. For the network capacity and efficiency trade-off, we construct the MSFA module with one bidirectional (up-sampling and down-sampling) path followed by an up-sampling path. Compared to PANet and BiFPN, the MSFA ends with an up-sampling path to support high-resolution prediction. In addition, the MSFA module is more efficient than BiFPN due to the fewer bidirectional paths. On the other hand, these previous networks utilize the feature maps from C3 and above of the backbone network; except for these feature maps, the MSFA module also fuses the feature maps from L1 and L2 to generate higher-resolution feature maps.
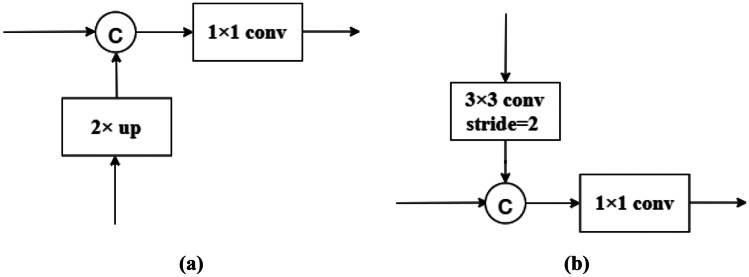
Figure 3a shows the feature fusion block of the up-sampling path in the MSFA module. In this block, the coarser-resolution feature maps are up-sampled by a factor of 2 and channel-wisely concatenated with the feature maps from the previous down-sampling path having the same resolution. And the concatenated feature maps go through a convolution layer to reduce the number of channels to 256. In the second up-sampling path, we reduce the number of channels to 128 at L2 and 64 at L1 and perform a and convolution at the end of the path to regress heatmaps.
Fig. 3.
Feature fusion blocks of the up-sampling and down-sampling paths. a A feature fusion block of the up-sampling path, b a feature fusion block of the down-sampling path
Figure 3b shows the feature fusion block of the down-sampling path. In this block, the finer-resolution feature maps are down-sampled by a convolution with stride 2. The number of channels is doubled to compensate for the loss of information caused by the decrease in resolution. The down-sampled feature maps are channel-wisely concatenated with the feature maps from the previous up-sampling path having the same resolution. And the number of channels is reduced back to that of the down-sampled feature maps by a convolution.
In the above feature fusion blocks, the feature maps with higher resolution are emphasized by keeping more channels than those with lower resolution. This higher-resolution-dominate strategy will help to high-resolution heatmap regression. In previous methods [46, 47, 55], feature maps with different resolutions are merged by addition, requiring them to have not only the same resolution but also the same channel size, which is not flexible as our feature fusion approach. After merging feature maps with different resolutions, we use a convolution instead of a one used in the previous methods to reduce the number of channels, and the number of parameters in this convolutional layer is largely reduced.
Feature Refinement Module
The feature maps output from MSFA has half the resolution of the input image. To achieve more accurate prediction, we introduce the feature refinement (FR) module to generate feature maps having the same resolution as the input image. In the FR module, a convolution is performed over the input image, and the result feature maps (32 channels) are concatenated with the up-sampled feature maps (64 channels) and heatmaps from the MSFA module. The predicted heatmaps from the MSFA module are introduced here to guide the heatmap regression in the FR module. The concatenated feature maps have the same resolution as the input image and are the highest resolution ever used in literature. Finally, we perform a convolution and a convolution over the concatenated feature maps for heatmap regression.
Ground-Truth
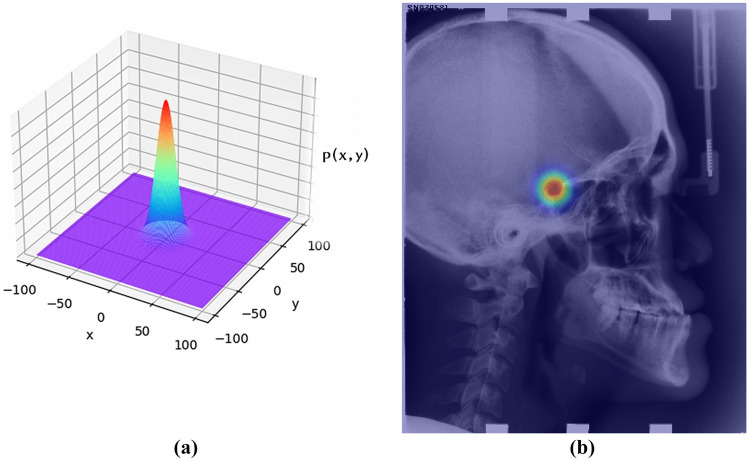
Each of the ground-truth heatmap is generated by applying an unnormalized Gaussian kernel (without the normalizing constant) to a specific landmark location. The ground-truth value at (i, j) in the heatmap for landmark k is defined as the following,
| 1 |
where is the ground-truth position of landmark k in a heatmap and controls the spread of the peak. A heatmap represents the pseudo-probability or confidence of a specific landmark at each spatial position. An example heatmap is given in Fig. 4b. When the ground-truth heatmaps are used to train a CNN, the coordinate regression is transferred to the heatmap regression. At test time, the coordinates of landmarks are recovered by performing non-maximum suppression (NMS) over the predicted heatmaps.
Fig. 4.
Visualization of heatmap. a The shape of a 2D Gaussian distribution, b the heatmap of the first landmark layered over the original image
Before encoding coordinates into heatmaps, the original image needs to be down-sampled to the input size of the CNN. Accordingly, the ground-truth joint coordinates are also downsampled and quantized to get the coordinates in heatmaps. The heatmaps generated in this way are inaccurate due to the quantization error. To alleviate this problem, we follow [60] to use the non-quantized coordinates to generate more accurate heatmaps.
Exponential Weighted Center Loss for Heatmap Regression
In previous methods for heatmap regression, the commonly used MSE loss is as the following,
| 2 |
where is the loss, and are the pixel’s intensities at position (i, j) in the predicted heatmap and the ground-truth heatmap of landmark k, respectively, W and H are the width and height of heatmaps, and K is the number of landmarks. The loss for an image is the average of the L2 loss over pixels in heatmaps of all landmarks, and all pixels have the same weight in the function.
The heatmap regression tries to approach the unnormalized Gaussian distribution centered at each ground-truth landmark, then NMS is used to determine the landmark’s coordinates. Therefore, the regression accuracy at pixels near a landmark is more critical for the accurate localization of landmarks. On the contrary, the prediction accuracy at pixels far from a landmark is less critical since moderate errors on these pixels will not affect landmark localization. The above intuition suggests that the loss function can be weighted according to the intensity of pixels in the ground-truth heatmaps to focus on the errors at pixels near landmarks.
Based on the analysis above, we proposed a novel loss function named Exponential Weighted Center loss for heatmap regression, which is defined as follows:
| 3 |
where is a hyper-parameter. From this equation, we can see that the error at a position of a heatmap is weighted by an exponential function of the ground-truth intensity y there. The EWC loss function is also illustrated in Fig. 5, in which the horizontal axis denotes the error between the predicted and ground-truth intensities of a pixel, and the vertical axis represents the loss. At each landmark, the weight reaches the maximum of , and the error there is heavily enlarged. On the other hand, when moving away from a landmark, the weight reduces exponentially to 1 when y is approaching 0. Therefore, more attention is paid to the errors near a landmark than to the errors far away from it. In other words, the loss function focuses on the errors near a landmark and is less sensitive to the errors from the background area in an image. In our study, we set to 40 to get good performance.
Fig. 5.
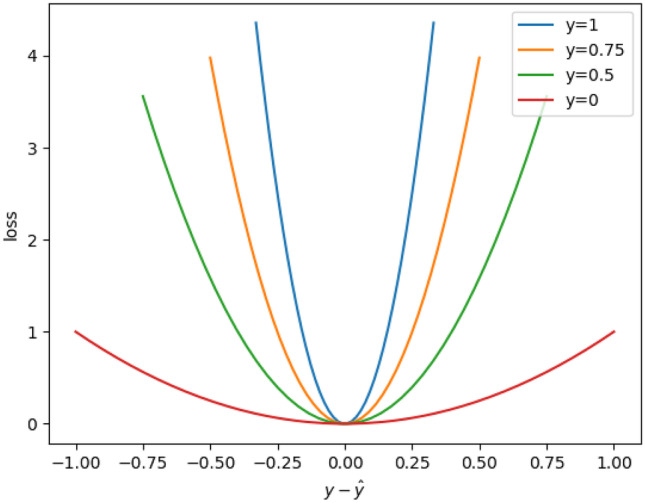
The EWC loss function ()
Coarse-to-fine Supervision
In [61], it is indicated that intermediate supervision plays an essential role in improving the performance of a deep neural network. We also introduce intermediate supervision to the MSFA module for more accurate landmark prediction. Both the output feature maps and heatmaps of our MSFA module have 1/2 resolution as the input image, so we set its ground-truth heatmaps to the same resolution. The predicted heatmaps of our FR module have the same resolution as the input image, and so do its ground-truth heatmaps. We set the kernel size of the ground-truth heatmaps for the two modules to the same value, which means that the ground-truth heatmaps for the MSFA module are coarser than those for the FR module. Finally, the losses from the two modules are equally summed as the overall loss, resulting in multi-scale coarse-to-fine supervision. Our experimental results demonstrate that the coarse-to-fine supervision can refine the localization.
Experiments and Results
Datasets
In this paper, we evaluate our landmark detection network on three public benchmark datasets: the cephalometric radiograph dataset [4], the hand radiograph dataset [37], and the spinal anterior-posterior (AP) radiograph dataset [33]. The example of these three datasets and their typical landmarks are shown in Fig. 1.
Cephalometric Radiographs
The cephalometric radiograph dataset is provided by the ISBI 2015 Grand Challenge in Automatic Detection and Analysis for Diagnosis in Cephalometric X-ray Images [4]. It consists of 400 lateral cephalometric X-ray images from 400 subjects, with 19 annotated landmarks labeled by two experienced doctors. Each image has a resolution of , and each pixel is about 0.1mm. The dataset is split into a training dataset of 150 images, a Test1 dataset of 150 images, and a Test2 dataset of 100 images. We use the training dataset for training, the Test1 dataset for validation, and the Test2 dataset for testing. We adopt the evaluation metrics used in the ISBI 2015 Challenge [4], including the mean radial error (MRE, in millimeter, the smaller, the better), and the successful detection rate (SDR, the bigger, the better) in radius (2.0mm, 2.5mm, 3.0mm, 4.0mm). MRE is defined as the average distance between predicted and ground-truth landmarks, and SDR is the percentage of predicted landmarks within a pre-defined range of ground-truth landmarks. We take the average of two doctors’ annotations as ground truth.
Hand Radiographs
The hand radiograph dataset contains 895 X-ray images of left hands with an average size of pixels from a publicly available Digital Hand Atlas1. In [37], the annotations of 37 characteristic landmarks on fingertips and bone joints are provided. Following [37], we normalize the image resolution according to wrist widths and adopt the three-fold cross-validation setup, which splits images into approximately 600 training and 300 testing images per fold. The evaluation metrics include the mean radial error (MRE, in mm) and the successful detection rate (SDR) in radius (2mm, 4mm, 10mm).
Spinal Anterior-Posterior Radiographs
The spinal AP radiograph dataset contains 481 spinal anterior-posterior X-ray images provided by clinicians [33]. Seventeen vertebrae composed of the thoracic and lumbar spine are selected for spinal shape characterization. Each vertebra is located by four landmarks at four corners, thus resulting in 68 landmarks per spinal image. Following [33], the dataset is split into 431 for training/validation and 50 for testing. Since the authors of [33] have not shared their data split, we split the data randomly. The evaluation metrics include the MSE and Pearson correlation coefficient () between the predicted landmarks and annotated ground truth.
Implementation Details
Our network is implemented by PyTorch 1.0.1 and Python 3.6. For the cephalometric radiograph dataset, the input image is resized to , and no data augmentation is performed. For the hand radiograph dataset, the input image is resized to , and data augmentation is employed following [37]. For the spinal AP radiograph dataset, the input image is resized to , and data augmentation is performed following [33]. Through experimental comparison, we set the kernel size , which is a parameter used to generate the ground-truth heatmaps, to 10 and the hyper-parameter to 40. The network is optimized by the Adadelta optimizer, and the learning rate is 0.0001. The backbone parameters are optimized along with the entire network. We train our network for 300 epochs on a GTX 2080TI GPU with a mini-batch size of 1.
Landmark Detection Results
Cephalometric Radiographs
We first compare our method with prior state-of-the-art methods on the cephalometric X-ray dataset. All the experimental results on Test1 data and Test2 data are shown in Table 1.
Table 1.
Comparison of our FARNet with prior state-of-the-art methods on the cephalometric X-ray dataset with 19 annotated landmarks
| Test1 data | Test2 data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | Input size | MRE | 2mm | 2.5mm | 3mm | 4mm | MRE | 2mm | 2.5mm | 3mm | 4mm |
| Ibragimov et al. [20] | - | 1.84 | 71.70 | 77.40 | 81.90 | 88.00 | - | 62.74 | 70.47 | 76.53 | 85.11 |
| Lindner et al. [25] | - | 1.67 | 74.95 | 80.28 | 84.56 | 89.68 | 1.92 | 66.11 | 72.00 | 77.63 | 87.42 |
| Arik et al. [31] | - | 75.37 | 80.91 | 84.32 | 88.25 | - | 67.68 | 74.16 | 79.11 | 84.63 | |
| Qian et al. [44] | - | - | 82.50 | 86.20 | 89.30 | 92.60 | - | 72.40 | 76.15 | 79.65 | 85.90 |
| Oh et al. [43] | 1.18 | 86.20 | 91.20 | 94.40 | 97.70 | 1.44 | 75.89 | 83.36 | 89.26 | 95.73 | |
| Chen et al. [42] | 1.17 | 86.67 | 92.67 | 95.54 | 98.53 | 1.48 | 75.05 | 82.84 | 88.53 | 95.05 | |
| Zhong et al. [38] | 1.12 | 86.91 | 91.82 | 94.88 | 97.90 | 1.42 | 76.00 | 82.90 | 88.74 | 94.32 | |
| FARNet(Our) | 1.12 | 88.03 | 92.73 | 95.96 | 98.48 | 1.42 | 77.00 | 84.42 | 89.47 | 95.21 | |
The bold value in each column represents the best result
Ibragimov et al. [20] and Lindner et al. [25] combined the random forest regression-voting and the statistical shape analysis techniques and have achieved the best performances in the IEEE ISBI 2014 [3] and 2015 Challenges [4] respectively. Ibragimov’s method obtains the MRE of 1.84 mm on Test1 data and the SDRs of 71.70% and 62.74% on Test1 and Test2 data, respectively, in a 2-mm precision range, which is the acceptable precision range in clinical practice. In the following description, we only mention the SDRs in this range.
Lindner’s method makes an improvement and achieves the MRE of 1.67 mm on Test1 data and the SDRs of 74.95% and 66.11% on Test1 and Test2 data, respectively. Arik et al. [31] combined a CNN with a shape-based model for landmark detection. Their method achieves the SDRs of 75.37% and 67.68% on Test1 and Test2 data, respectively. Qian et al. [44] utilized Faster R-CNN to detect landmarks and a two-stage repair strategy to remove the abnormal candidate landmarks. Their method makes a remarkable improvement over previous methods and achieves the SDRs of 82.50% and 72.40% on Test1 and Test2 data, respectively. DACFL [43] learns richer representations and achieves the SDRs of 86.20% and 75.89% on Test1 and Test2 data respectively. Chen et al. [42] combined multi-scale features from a pre-trained backbone network and employed a self-attention mechanism for landmark detection. Their method further improves and achieves the SDRs of 86.67% and 75.05% on Test1 and Test2 data, respectively. Zhong et al. [38] first utilized a global U-Net to regress coarse heatmaps from a downsized image and utilized the heatmaps to guide a patch-based U-Net to regress heatmaps in high resolution. Their method achieves the SDRs of 86.91% and 76.00% on Test1 and Test2 data, respectively. Finally, our FARNet makes 1.12 and 1.00 points improvements of SDRs on Test1 and Test2 data, respectively, over the second-best method [38].
Considering all evaluation metrics, we can see that our method achieves the best results except for the SDR in a radius of 4mm, on which our result is only 0.05 below that of the work [42]. We conjecture that this slight lag is mainly because our loss function focuses on the errors at the pixels near a landmark. However, the SDR in a smaller range is more important than the one in a larger range because it measures the predictions with a smaller deviation.
Although the differences in performance between our method and the previous state-of-the-art methods [38, 42, 43] are not of clinical significance, our method has its advantages in engineering. DACFL [43] forces the CNN to learn richer representations by perturbing the local appearance of training images, resulting in a more complex training process. Chen et al. [42] utilized a self-attention mechanism to construct weighted feature maps for different landmarks separately, which greatly increases the number of parameters and the consumption of memory storage. Zhong et al. [38] proposed two-stage U-Nets for landmark detection, which leads to inefficient training and testing. Our method avoids all these shortcomings.
In the cephalometric X-ray dataset, the landmarks are labeled by two experienced doctors. We investigate the inter-observer variability based on the distance between the annotations of the two doctors. The means and standard deviations of the distances over images and landmarks for the training set, Test1, and Test2 set are , , and , respectively. The MRE of our method is below the inter-observer variability for both Test1 and Test2 sets.
Hand Radiographs
To evaluate our deep network on the hand X-ray dataset, we follow the standards of Payer et al. [37] and use three-fold cross-validation. We compare our method with their method, which achieved the best results recently, and also with other prior state-of-the-art methods [23, 24, 26, 28]. The results are shown in Table 2. The prior state-of-the-art methods are mainly random forest–based approaches. Among them, Lindner et al. [24] obtained the best SDR of 93.68% in the 2-mm precision range, and S̆tern et al. [26] achieved the best MRE of 0.80mm. Payer et al. [37] combined U-Net with a learned global configuration for landmark localization and greatly improved the performance. Their method obtains the SDR of 94.99% and the MRE of 0.66mm. Our FARNet remarkably improves the performance and achieves the SDR of 97.24% and the MRE of 0.62mm.
Table 2.
Landmark localization results from a three-fold cross validation on the hand X-ray dataset with 37 annotated landmarks and compare with other methods
| Methods | Input size | MRE ± Std (mm) | 2mm (%) | 4mm (%) | 10 mm (%) |
|---|---|---|---|---|---|
| Urschler et al. [28] | 0.80 ± 0.93 | 92.19 | 98.46 | 99.95 | |
| S̆tern et al. [26] | 0.80 ± 0.91 | 92.20 | 98.45 | 99.95 | |
| Ebner et al. [23] | 0.97 ± 2.45 | 91.60 | 97.84 | 99.31 | |
| Lindner et al. [24] | 0.85 ± 1.01 | 93.68 | 98.95 | 99.94 | |
| Payer et al. [37] | 0.66 ± 0.74 | 94.99 | 99.27 | 99.99 | |
| FARNet(Our) | 0.62 ± 0.55 | 97.24 | 99.8 | 100 |
The bold value in each column represents the best result
Spinal Anterior-posterior Radiographs
In this experiment, we evaluate our FARNet on the public spinal anterior-posterior X-ray dataset [33] and compare our method with BoostNet [33] and other baseline methods on this dataset. We conduct a 5-fold cross-validation on the Trainset and evaluate them on the Test data. The MSE and Pearson correlation coefficient () are used as the evaluation metrics. The unit for MSE is a fraction of the original image (e.g., 0.010 MSE represents an average of 10-pixel error in a image). The experimental results are shown in Table 3. From it, we can see that our method outperforms previous methods by large margins, which proves its effectiveness and generality.
Table 3.
Landmark localization results on the spinal anterior-posterior X-ray dataset with 68 annotated landmarks and compare with other methods. The units of MSE are the fraction of orinal image (0.010 MSE represents average of 10-pixel error in a image)
| Methods | MSE (fraction of image) | |
|---|---|---|
| SVR [27] | 0.006 | 0.93 |
| RFR [21] | 0.0052 | 0.94 |
| BoostNet [33] | 0.0046 | 0.94 |
| FARNet(Our) | 0.0017 | 0.98 |
The bold value in each column represents the best result
Visualization of Anatomical Landmark Detection
Figure 6 shows some representative results by our network on the three datasets. The red points denote the landmarks detected by our network, and the blue points represent the ground-truth landmarks.
Fig. 6.
Illustration of landmark detection results by our proposed method on three public datasets. The first row is for cephalometric radiographs (19 landmarks), the second row is for hand radiographs (37 landmarks), and the last row is for spinal anterior-posterior radiographs (68 landmarks). The red points denote the predicted landmarks by our network, while blue points represent the ground-truth landmarks
Discussion
In this section, we analyze the influences of the important factors of our method based on the experiments on the Test1 data of the cephalometric Xradiograph dataset. We also elaborate on the limitation of our method and give the future direction.
Influence of Backbone Networks
We first conduct experiments to compare several popular backbone networks, including VGG, ResNet, and DenseNet. ResNet and DenseNet have a similar structure, as shown in Fig. 2. VGG has five convolutional blocks corresponding to . Therefore, our FR module directly combines the first block’s output feature maps with the up-sampled feature maps and heatmaps from the MSFA module. As shown in Table 4, DenseNet-121 has achieved the best performance; hence, we adopt it in our network. On the contrary, VGGNets need a much longer training time (900 epochs) to converge and obtain the worst performances.
Table 4.
Comparison of different backbone networks on the Test1 data of the cephalometric X-ray dataset
| MRE | 2mm | 2.5mm | 3mm | 4mm | |
|---|---|---|---|---|---|
| VGG-16 | 1.44 | 84.03 | 90.70 | 93.81 | 97.29 |
| VGG-19 | 1.37 | 82.31 | 89.08 | 92.98 | 96.87 |
| ResNet-101 | 1.19 | 86.49 | 92.28 | 95.40 | 98.07 |
| ResNet-152 | 1.29 | 86.76 | 92.42 | 95.33 | 98.03 |
| DenseNet-169 | 1.15 | 87.64 | 92.13 | 95.49 | 98.38 |
| DenseNet-121 | 1.12 | 88.03 | 92.73 | 95.96 | 98.48 |
The bold value in each column represents the best result
Influence of FARNet Components
We also conduct ablation studies to understand the merit of the FARNet components. The components evaluated include our MSFA module, FR module, coarse-to-fine supervision, and the proposed Exponential Weighted Center (EWC) loss function. In addition, to validate our multi-scale feature fusion, we implement another version of the MSFA module, MSFA(+), which follows FPN [46] and PAN [47] to merge features by addition and uses the same channel size setting. To evaluate the gain of coarse-to-fine supervision, we develop a naïve version (suffixed by *) of the FR module with no supervision on the MSFA and thus no heatmap from the MSFA introduced to the FR module. We compare our network with the popular U-Net [49] and FPN [46] to validate our backbone and MSFA module. The MSE loss is used in all testing methods mentioned above. Finally, we evaluate the full version of FARNet, which employs the Exponential Weighted Center loss.
The results in Table 5 show that the original U-Net achieves the worst results among the comparing methods. Our network with only the backbone and the MSFA module (MSFA) can outperform it in all metrics by a large margin (MRE reduced by 0.21, SDR in 2.0mm improved by 1.72). This is because U-Net is very shallow, the pre-trained backbone used in our network can extract more powerful features, and our MSFA module enables more high-level feature fusion. For a fair comparison, we also adopt DenseNet-121 as the backbone for FPN. After upsampling the finest feature maps from FPN to the resolution of the input image, and convolution layers are performed on them to regression heatmaps. We can see from the experimental results that FPN is better than U-Net, mainly due to the backbone used. MSFA(+) outperforms FPN, which indicates one more down-sampling and up-sampling path can make a better feature fusion. And our MSFA module can further improve over MSFA(+) due to its more flexible feature fusion strategy.
Table 5.
Ablation study: the MSFA module, naïve FR module, coarse-to-fine supervision, and the proposed Exponential Weighted Center loss function
| MRE | 2mm | 2.5mm | 3mm | 4mm | |
|---|---|---|---|---|---|
| U-Net | 1.38 | 84.45 | 90.45 | 93.57 | 97.33 |
| FPN | 1.19 | 85.47 | 92.17 | 95.54 | 98.24 |
| MSFA(+) | 1.18 | 85.73 | 92.31 | 95.83 | 98.36 |
| MSFA | 1.17 | 86.17 | 92.42 | 95.64 | 98.38 |
| MSFA+FR* | 1.16 | 86.91 | 92.63 | 95.68 | 98.45 |
| MSFA+FR | 1.15 | 87.43 | 93.01 | 95.85 | 98.45 |
| MSFA+FR+EWC | 1.12 | 88.03 | 92.73 | 95.96 | 98.48 |
The bold value in each column represents the best result
The naïve version of the FR module (FR*) reduces MRE by 0.01 and improves SDR in 2.0mm by 0.74. When applying coarse-to-fine supervision to the FR module and MSFA module and introducing the up-sampled heatmaps from MSFA to the FR module, the FR module further reduces MRE by 0.01 and improves SDR in 2.0mm by 0.52. This validates the use of coarse-to-fine supervision and the heatmap-guide strategy. Finally, when employing the Exponential Weighted Center loss in the supervision, our FARNet reduces MRE by 0.03, improves SDR in 2.0mm by 0.6, and achieves the best performance. These results indicate that the proposed components can consistently improve the accuracy of landmark localization.
Influence of Loss Function
We compare our EWC loss with L1, smooth L1, MSE, and the Adaptive Wing (AW) loss and give the experimental results in Table 6. The AW loss has four hyper-parameters which are hard to tune, so we use the hyper-parameter settings suggested by the authors [57] in our experiment. From the results, we can observe that the L1 loss gets the worst performance, but the smooth L1 loss improves and even outperforms the MSE and AW loss on MRE and SDR in a radius of 2mm. The AW loss achieves the performance inferior but close to the MSE loss. Overall, our EWC loss achieves the best results on all metrics except for SDR in a radius of 2.5mm, on which the MSE loss is best.
Table 6.
Lose function comparison
| MRE | 2mm | 2.5mm | 3mm | 4mm | |
|---|---|---|---|---|---|
| L1 | 1.16 | 86.93 | 92.31 | 95.85 | 98.45 |
| Smooth L1 | 1.14 | 87.46 | 92.93 | 95.68 | 98.38 |
| AW | 1.15 | 87.08 | 92.31 | 95.64 | 98.38 |
| MSE | 1.15 | 87.43 | 93.01 | 95.85 | 98.45 |
| EWC | 1.12 | 88.03 | 92.73 | 95.96 | 98.48 |
The bold value in each column represents the best result
Influence of Hyper-parameter
To investigate the influence of the hyper-parameter , we evaluate our method with five values , respectively, and give the MREs with respect to different values in Fig. 7. It can be observed that our method reaches the best results when is set to 40.
Fig. 7.
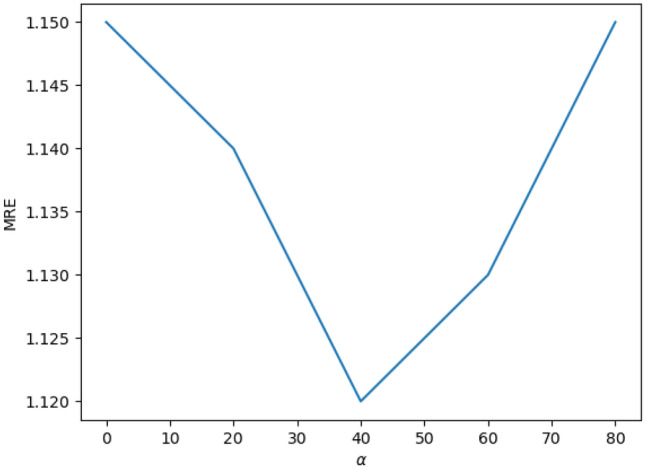
MRE versus
Limitation and Future Direction
The main limitation of our network is that it works for 2D medical images. Although many research works have been conducted for 2D anatomical landmark detection (please see the “Deep Learning Methods for Anatomical Landmark Detection” section), landmark detection for 3D medical images has much more applications. Therefore, we will extend our network to 3D medical images in the future.
For 2D images, there are lots of large annotated datasets, such as ImageNet [59], PASCAL VOC [62], and MS COCO [63]. The pre-trained models based on these datasets can extract powerful general features, which can accelerate the training convergence speed and improve the accuracy of the target model. Our work demonstrates the effectiveness of the pre-trained network for 2D medical landmark detection. But for 3D images, the annotated datasets are usually too small to stably pre-train a 3D model. Some works used the networks pre-trained on the Kinetics dataset [64]. However, the large differences in data domain distribution between the temporal video data and the medical volume data will deteriorate the transfer effect. Recently, Chen et al. [65] constructed a large 3D medical dataset, 3DSeg-8, with diverse modalities, target organs, and pathologies and trained a network called Med3D on the 3DSeg-8 dataset to build a series of pre-trained models. Med3D employs the encoder-decoder structure and adopts the family of ResNet as the backbone by replacing all 2D convolution kernels with the 3D version.
To extend our FARNet, we can use the backbone pre-trained on the 3DSeg-8 dataset as the encoder of our network and replace all 2D convolution kernels in the MSFA and FR modules with 3D ones. In addition, we can reduce the number of convolutional channels in the MSFA and FR modules to reduce the model size.
Conclusion
This paper proposes a novel end-to-end deep network for anatomical landmark detection. Our network includes a backbone, a feature aggregation, and a feature refinement module. The backbone network pre-trained on natural images is used to extract a feature hierarchy. The feature aggregation module is used to fuse multi-scale features extracted by the backbone network, and the feature refine module is proposed to generate high-resolution feature maps. Coarse-to-fine supervisions are applied to the two modules to facilitate end-to-end training. We further propose a novel loss function for accurate heatmap regression, which concentrates on the errors at the pixels near landmarks and suppresses the ones from far away. Our network has achieved state-of-the-art performances on three publicly available anatomical landmark detection datasets, demonstrating our network’s effectiveness and generality. And the end-to-end nature of our network makes it more efficient than the previous patch-based approaches.
Author Contribution
Both authors contributed to the study’s conception and design. In addition, Yueyuan Ao performed material preparation, data collection and analysis, and coding. Both authors participated in writing and revising the manuscript, and Hong Wu contributed the most. All authors have read and approved the final manuscript.
Declarations
Competing Interests
The authors declare no competing interests.
Footnotes
Digital Hand Atlas Database System, www.ipilab.org/BAAweb
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Yueyuan Ao, Email: aoyueyuan@qq.com.
Hong Wu, Email: hwu@uestc.edu.cn.
References
- 1.Razvan Ioan Ionasec, Bogdan Georgescu, Eva Gassner, Sebastian Vogt, Oliver Kutter, Michael Scheuering, Nassir Navab, and Dorin Comaniciu. Dynamic model-driven quantitative and visual evaluation of the aortic valve from 4d ct. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 686–694. Springer, 2008. [DOI] [PubMed]
- 2.Yefeng Zheng, Matthias John, Rui Liao, Jan Boese, Uwe Kirschstein, Bogdan Georgescu, S Kevin Zhou, Jörg Kempfert, Thomas Walther, Gernot Brockmann, et al. Automatic aorta segmentation and valve landmark detection in c-arm ct: application to aortic valve implantation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 476–483. Springer, 2010. [DOI] [PubMed]
- 3.Wang Ching-Wei, Huang Cheng-Ta, Hsieh Meng-Che, Li Chung-Hsing, Chang Sheng-Wei, Li Wei-Cheng, Vandaele Rémy, Marée Raphaël, Jodogne Sébastien, Geurts Pierre, et al. Evaluation and comparison of anatomical landmark detection methods for cephalometric x-ray images: a grand challenge. IEEE transactions on medical imaging. 2015;34(9):1890–1900. doi: 10.1109/TMI.2015.2412951. [DOI] [PubMed] [Google Scholar]
- 4.Wang Ching-Wei, Huang Cheng-Ta, Lee Jia-Hong, Li Chung-Hsing, Chang Sheng-Wei, Siao Ming-Jhih, Lai Tat-Ming, Ibragimov Bulat, Vrtovec Tomaž, Ronneberger Olaf, et al. A benchmark for comparison of dental radiography analysis algorithms. Medical image analysis. 2016;31:63–76. doi: 10.1016/j.media.2016.02.004. [DOI] [PubMed] [Google Scholar]
- 5.Keelin Murphy, Bram van Ginneken, Stefan Klein, Marius Staring, Bartjan J de Hoop, Max A Viergever, and Josien PW Pluim. Semi-automatic construction of reference standards for evaluation of image registration. Medical image analysis, 15(1):71–84, 2011. [DOI] [PubMed]
- 6.Han Dong, Gao Yaozong, Guorong Wu. Pew Thian Yap, and Dinggang Shen. In Medical Image Computing and Computer-Assisted Intervention (MICCAI): Robust anatomical landmark detection for mr brain image registration; 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ozan Oktay, Wenjia Bai, Ricardo Guerrero, Martin Rajchl, Antonio de Marvao, Declan P O’Regan, Stuart A Cook, Mattias P Heinrich, Ben Glocker, and Daniel Rueckert. Stratified decision forests for accurate anatomical landmark localization in cardiac images. IEEE transactions on medical imaging, 36(1):332–342, 2016. [DOI] [PubMed]
- 8.Rudolph DJ, Sinclair PM, Coggins JM. Automatic computerized radiographic identification of cephalometric landmarks. American Journal of Orthodontics and Dentofacial Orthopedics. 1998;113(2):173–179. doi: 10.1016/S0889-5406(98)70289-6. [DOI] [PubMed] [Google Scholar]
- 9.Vicente Grau, M Alcaniz, MC Juan, Carlos Monserrat, and Christian Knoll. Automatic localization of cephalometric landmarks. Journal of Biomedical Informatics, 34(3):146–156, 2001. [DOI] [PubMed]
- 10.John Cardillo and Maher A Sid-Ahmed. An image processing system for locating craniofacial landmarks. IEEE transactions on medical imaging, 13(2):275–289, 1994. [DOI] [PubMed]
- 11.Idris El-Feghi, Maher A Sid-Ahmed, and Majid Ahmadi. Automatic localization of craniofacial landmarks for assisted cephalometry. Pattern Recognition, 37(3):609–621, 2004.
- 12.Saad AA, El-Bialy A, Kandil AH, Sayed AA. Automatic cephalometric analysis using active appearance model and simulated annealing. ICGST Int J on Graphics, Vision and Image Processing, Special Issue on Image Retrieval and Representation. 2006;6:51–67. [Google Scholar]
- 13.Yue Weining, Yin Dali, Li Chengjun, Wang Guoping, Tianmin Xu. Automated 2-d cephalometric analysis on x-ray images by a model-based approach. IEEE transactions on biomedical engineering. 2006;53(8):1615–1623. doi: 10.1109/TBME.2006.876638. [DOI] [PubMed] [Google Scholar]
- 14.Rahele Kafieh, Alireza Mehri, and Saeed Sadri. Automatic landmark detection in cephalometry using a modified active shape model with sub image matching. In 2007 International Conference on Machine Vision, pages 73–78. IEEE, 2007.
- 15.Johannes Keustermans, Wouter Mollemans, Dirk Vandermeulen, and Paul Suetens. Automated cephalometric landmark identification using shape and local appearance models. In 2010 20th International Conference on Pattern Recognition, pages 2464–2467. IEEE, 2010.
- 16.S. Chakrabartty, M. Yagi, T. Shibata, and G. Cauwenberghs. Robust cephalometric landmark identification using support vector machines. In International Conference on Multimedia & Expo, 2003.
- 17.Daniela Giordano, Rosalia Leonardi, Francesco Maiorana, Gabriele Cristaldi, and Maria Luisa Distefano. Automatic landmarking of cephalograms by cellular neural networks. In Conference on Artificial Intelligence in Medicine in Europe, 2005.
- 18.Antonio Criminisi, Jamie Shotton, and Stefano Bucciarelli. Decision forests with long-range spatial context for organ localization in ct volumes. In Medical Image Computing and Computer-Assisted Intervention (MICCAI), pages 69–80, 2009.
- 19.Yiqiang Zhan, Maneesh Dewan, Martin Harder, Arun Krishnan, and Xiang Sean Zhou. Robust automatic knee mr slice positioning through redundant and hierarchical anatomy detection. IEEE transactions on medical imaging, 30(12):2087–2100, 2011. [DOI] [PubMed]
- 20.Bulat Ibragimov, Boštjan Likar, F Pernus, and Tomaž Vrtovec. Computerized cephalometry by game theory with shape-and appearance-based landmark refinement. In Proceedings of International Symposium on Biomedical imaging (ISBI), 2015.
- 21.Antonio Criminisi, Jamie Shotton, Duncan Robertson, and Ender Konukoglu. Regression forests for efficient anatomy detection and localization in ct studies. In International MICCAI Workshop on Medical Computer Vision, pages 106–117. Springer, 2010.
- 22.Criminisi A, Robertson D, Konukoglu E, Shotton J, Pathak S, White S, Siddiqui K. Regression forests for efficient anatomy detection and localization in computed tomography scans. Medical Image Analysis. 2013;17(8):1293–1303. doi: 10.1016/j.media.2013.01.001. [DOI] [PubMed] [Google Scholar]
- 23.Thomas Ebner, Darko Stern, Rene Donner, Horst Bischof, and Martin Urschler. Towards automatic bone age estimation from mri: localization of 3d anatomical landmarks. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 421–428. Springer, 2014. [DOI] [PubMed]
- 24.Claudia Lindner, Paul A Bromiley, Mircea C Ionita, and Tim F Cootes. Robust and accurate shape model matching using random forest regression-voting. IEEE transactions on pattern analysis and machine intelligence, 37(9):1862–1874, 2014. [DOI] [PubMed]
- 25.Claudia Lindner and Tim F Cootes. Fully automatic cephalometric evaluation using random forest regression-voting. In IEEE International Symposium on Biomedical Imaging. Citeseer, 2015.
- 26.Darko Štern, Thomas Ebner, and Martin Urschler. From local to global random regression forests: Exploring anatomical landmark localization. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 221–229. Springer, 2016.
- 27.Haoliang Sun, Xiantong Zhen, Chris Bailey, Parham Rasoulinejad, Yilong Yin, and Shuo Li. Direct estimation of spinal cobb angles by structured multi-output regression. In International conference on information processing in medical imaging, pages 529–540. Springer, 2017.
- 28.Urschler Martin, Ebner Thomas, Štern Darko. Integrating geometric configuration and appearance information into a unified framework for anatomical landmark localization. Medical image analysis. 2018;43:23–36. doi: 10.1016/j.media.2017.09.003. [DOI] [PubMed] [Google Scholar]
- 29.Omar Emad, Inas A. Yassine, and Ahmed S. Fahmy. Automatic localization of the left ventricle in cardiac mri images using deep learning. In International Conference of the IEEE Engineering in Medicine & Biology Society, 2015. [DOI] [PubMed]
- 30.Benjamin Aubert, Carlos Vazquez, Thierry Cresson, Stefan Parent, and Jacques De Guise. Automatic spine and pelvis detection in frontal x-rays using deep neural networks for patch displacement learning. In IEEE International Symposium on Biomedical Imaging, 2016.
- 31.Sercan Ö Arik, Bulat Ibragimov, and Lei Xing. Fully automated quantitative cephalometry using convolutional neural networks. Journal of Medical Imaging, 4(1):014501, 2017. [DOI] [PMC free article] [PubMed]
- 32.Hansang Lee, Minseok Park, and Junmo Kim. Cephalometric landmark detection in dental x-ray images using convolutional neural networks. In Medical Imaging 2017: Computer-Aided Diagnosis, volume 10134, page 101341W. International Society for Optics and Photonics, 2017.
- 33.Hongbo Wu, Chris Bailey, Parham Rasoulinejad, and Shuo Li. Automatic landmark estimation for adolescent idiopathic scoliosis assessment using boostnet. In International Conference on Medical Image Computing and Computer-Assisted Intervention, 2017.
- 34.Gernot Riegler, Martin Urschler, Matthias Ruther, Horst Bischof, and Darko Stern. Anatomical landmark detection in medical applications driven by synthetic data. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 12–16, 2015.
- 35.Christian Payer, Darko Štern, Horst Bischof, and Martin Urschler. Regressing heatmaps for multiple landmark localization using cnns. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 230–238. Springer, 2016.
- 36.Alison Q O’Neil, Antanas Kascenas, Joseph Henry, Daniel Wyeth, Matthew Shepherd, Erin Beveridge, Lauren Clunie, Carrie Sansom, Evelina Seduikyte Keith Muir, and Ian Poole. Attaining human-level performance with atlas location autocontext for anatomical landmark detection in 3d ct data. In Proceedings of the European Conference on Computer Vision (ECCV), pages 0–0, 2018.
- 37.Payer Christian, Štern Darko, Bischof Horst, Urschler Martin. Integrating spatial configuration into heatmap regression based cnns for landmark localization. Medical Image Analysis. 2019;54:207–219. doi: 10.1016/j.media.2019.03.007. [DOI] [PubMed] [Google Scholar]
- 38.Zhusi Zhong, Jie Li, Zhenxi Zhang, Zhicheng Jiao, and Xinbo Gao. An attention-guided deep regression model for landmark detection in cephalograms. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 540–548. Springer, 2019.
- 39.Zhoubing Xu, Qiangui Huang, Jin Hyeong Park, Mingqing Chen, and S. Kevin Zhou. Supervised action classifier: Approaching landmark detection as image partitioning. In International Conference on Medical Image Computing and Computer-Assisted Intervention, 2017.
- 40.Alexander Toshev and Christian Szegedy. Deeppose: Human pose estimation via deep neural networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1653–1660, 2014.
- 41.Tomas Pfister, James Charles, and Andrew Zisserman. Flowing convnets for human pose estimation in videos. In Proceedings of the IEEE International Conference on Computer Vision, pages 1913–1921, 2015.
- 42.Runnan Chen, Yuexin Ma, Nenglun Chen, Daniel Lee, and Wenping Wang. Cephalometric landmark detection by attentive feature pyramid fusion and regression-voting. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 873–881. Springer, 2019.
- 43.Kanghan Oh, Il-Seok Oh, Lee Dae-Woo, et al. Deep anatomical context feature learning for cephalometric landmark detection. IEEE Journal of Biomedical and Health Informatics. 2021;25(3):806–817. doi: 10.1109/JBHI.2020.3002582. [DOI] [PubMed] [Google Scholar]
- 44.Jiahong Qian, Ming Cheng, Yubo Tao, Jun Lin, and Hai Lin. Cephanet: An improved faster r-cnn for cephalometric landmark detection. In 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), pages 868–871. IEEE, 2019.
- 45.Chuanbin Liu, Hongtao Xie, Sicheng Zhang, Zhendong Mao, Jun Sun, and Yongdong Zhang. Misshapen pelvis landmark detection with local-global feature learning for diagnosing developmental dysplasia of the hip. IEEE Transactions on Medical Imaging, 2020. [DOI] [PubMed]
- 46.Tsung-Yi Lin, Piotr Dollár, Ross Girshick, Kaiming He, Bharath Hariharan, and Serge Belongie. Feature pyramid networks for object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2117–2125, 2017.
- 47.Shu Liu, Lu Qi, Haifang Qin, Jianping Shi, and Jiaya Jia. Path aggregation network for instance segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 8759–8768, 2018.
- 48.Jonathan Long, Evan Shelhamer, and Trevor Darrell. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3431–3440, 2015. [DOI] [PubMed]
- 49.Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention, pages 234–241. Springer, 2015.
- 50.Liang-Chieh Chen, George Papandreou, Iasonas Kokkinos, Kevin Murphy, and Alan L Yuille. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE transactions on pattern analysis and machine intelligence, 40(4):834–848, 2017. [DOI] [PubMed]
- 51.Alejandro Newell, Kaiyu Yang, and Jia Deng. Stacked hourglass networks for human pose estimation. In European conference on computer vision, pages 483–499. Springer, 2016.
- 52.Bin Xiao, Haiping Wu, and Yichen Wei. Simple baselines for human pose estimation and tracking. In Proceedings of the European conference on computer vision (ECCV), pages 466–481, 2018.
- 53.Karen Simonyan and Andrew Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556, 2014.
- 54.Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
- 55.Mingxing Tan, Ruoming Pang, and Quoc V Le. Efficientdet: Scalable and efficient object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 10781–10790, 2020.
- 56.Zhen-Hua Feng, Josef Kittler, Muhammad Awais, Patrik Huber, and Xiao-Jun Wu. Wing loss for robust facial landmark localisation with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2235–2245, 2018.
- 57.Xinyao Wang, Liefeng Bo, and Li Fuxin. Adaptive wing loss for robust face alignment via heatmap regression. In Proceedings of the IEEE International Conference on Computer Vision, pages 6971–6981, 2019.
- 58.Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4700–4708, 2017.
- 59.Russakovsky Olga, Deng Jia, Hao Su, Krause Jonathan, Satheesh Sanjeev, Ma Sean, Huang Zhiheng, Karpathy Andrej, Khosla Aditya, Bernstein Michael. Imagenet large scale visual recognition challenge. International Journal of Computer Vision. 2015;115(3):211–252. doi: 10.1007/s11263-015-0816-y. [DOI] [Google Scholar]
- 60.Feng Zhang, Xiatian Zhu, Hanbin Dai, Mao Ye, and Ce Zhu. Distribution-aware coordinate representation for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7093–7102, 2020.
- 61.Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed, Dragomir Anguelov, Dumitru Erhan, Vincent Vanhoucke, and Andrew Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1–9, 2015.
- 62.Mark Everingham, Luc Van Gool, Christopher KI Williams, John Winn, and Andrew Zisserman. The pascal visual object classes (voc) challenge. International Journal of Computer Vision, 88(2):303-338, 2015.
- 63.Tsung-Yi Lin, Michael Maire, Serge Belongie, James Hays, Pietro Perona, Deva Ramanan, Piotr Dollár, and C Lawrence Zitnick. Microsoft coco: Common objects in context. In European Conference on Computer Vision, pages 740–755, 2014.
- 64.Will Kay, Joao Carreira, Karen Simonyan, Brian Zhang, Chloe Hillier, Sudheendra Vijayanarasimhan, Fabio Viola, Tim Green, Trevor Back, Paul Natsev, and et al. The kinetics human action video dataset. arXiv preprint arXiv:1705.06950, 2017.
- 65.Sihong Chen, Kai Ma, and Yefeng Zheng. Med3d: Transfer learning for 3d medical image analysis. arXiv preprint arXiv:1904.00625, 2019.