Fig. 7.

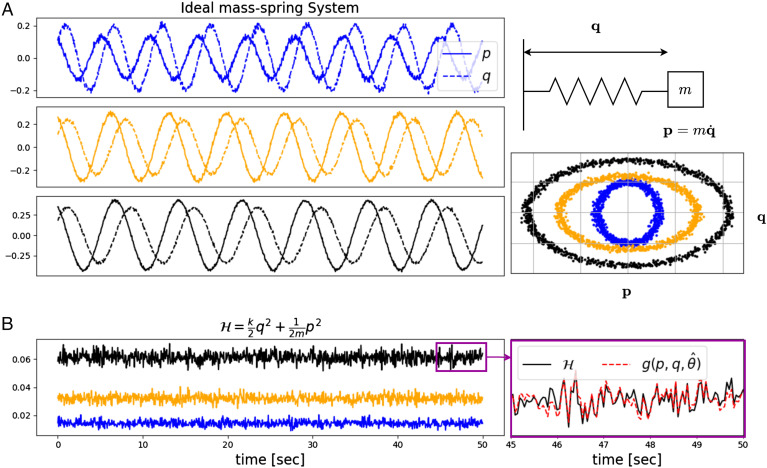
IRAS captures the conservation law in Hamiltonian mechanics. The dataset contains 100 different mass-spring systems. In each system, k and m were sampled uniformly between [0.5, 1.5] and the initial conditions, p₀ and q₀ between [0.15, 0.25] and [0.1, 0.2] respectively. The raw observations consist of times-series of length 1,000 of p and q corrupted by a zero-mean additive Gaussian white noise with SD 0.01. (A) Top Right: ideal mass on spring with mass m and spring constant k. Left: time traces of momentum, (p, solid lines) and coordinate, (q, dashed lines) for ideal mass–spring systems with spring and mass constants k = (0.72, 1.13, 1.05) and m = (0.59, 1.32, 1.48) in the Top, Middle, and Bottom panels, respectively. Bottom Right: same trajectories plotted in the phase plane (p, q). (B) Left: the energy as a function of time for the three systems in (A) with corresponding colors. Right: a zoom-in of the energy and output of the combination learned by IRAS in a short stretch of time.