Figure 3.

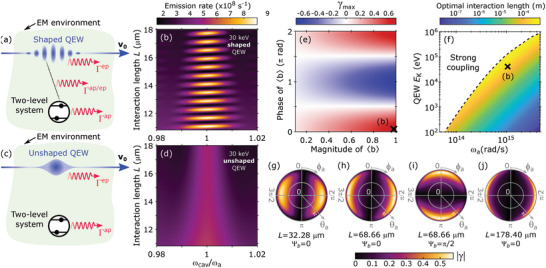
Quantum interference between distinguishable pathways provides a means to tailor spontaneous emission from free electrons and bound electrons via quantum waveshaping. a) Shaped quantum electron wavepackets (QEWs) and bound electrons (atomic two‐level system) within an electromagnetic (EM) environment separately emit photons at rates of Γ^ep and Γ^ap, respectively. Quantum interference between these spontaneous emission processes (dotted line) results in a third emission process at rate ${\mathrm{\Gamma }}^{\mathrm{ap}/\mathrm{ep}}$. This third emission process (the quantum interference term) can enhance or suppress the total spontaneous emission rate as a function of interaction length L (as shown in (b)) by more than 70%. c) In contrast, for unshaped incoming QEWs, quantum interference is absent (as shown in (d)) and the total spontaneous emission rate is ${\mathrm{\Gamma }}^{\mathrm{ap}}+{\mathrm{\Gamma }}^{\mathrm{ep}}$. Quantum interference can be tailored using the QEW and bound electron shapes, which are determined by bunching factor $⟨b⟩=|⟨b⟩|e^{i{\mathrm{\Psi }}_{\mathrm{b}}}$ and coherence ${\rho }_{\text{eg}}^{\mathrm{a}}=|{\rho }_{\text{eg}}^{\mathrm{a}}|e^{i{\varphi }_{\mathrm{a}}}$, respectively. Defining the figure of merit $\gamma ={\mathrm{\Gamma }}^{\mathrm{ap}/\mathrm{ep}}$/(${\mathrm{\Gamma }}^{\mathrm{ap}}+{\mathrm{\Gamma }}^{\mathrm{ep}}$), which is a measure of the quantum interference contribution, we see from (e) that larger |${\gamma }_{\max }$| = max(|γ|) is achieved for larger |$⟨b⟩$|, and that quantum interference can be tuned to enhance or suppress the spontaneous emission rate by controlling the phase of the bunching factor ${\mathrm{\Psi }}_{\mathrm{b}}$. (f) shows the dependence of the optimal length L _opt—at which ${\gamma }_{\max }$ is achieved—as a function of QEW kinetic energy $E_{\mathrm{K}}$ and bound electron emission frequency ${\omega }_{\mathrm{a}}$. The polar plots in (g–j) show the value of |γ| on the Bloch sphere representing the initial shape of the bound electron system at various values of L. (h,i) show that the profile of |γ| on the initial Bloch sphere can be manipulated by varying ${\mathrm{\Psi }}_{\mathrm{b}}$. Unless otherwise stated, we consider a 30 keV shaped QEW with $⟨b⟩=0.99$. Our two‐level, bound electron system is a Sn‐N vacancy with ${\omega }_{\mathrm{a}}$ ≈ 3 × 10¹⁵ rad s⁻¹ and transition dipole moment of $|\mathbf{d}|=4.33\times {10}^{-29}$ Cm aligned parallel to the field. For (g–j), the azimuthal angle ${\varphi }_{\mathrm{a}}$ is the phase of the bound electron coherence and θ_a is related to the excited state population through ${\cos }^2({\theta }_{\mathrm{a}}/2)$, and we use a 30 keV shaped QEW with $⟨b⟩=0.58$.