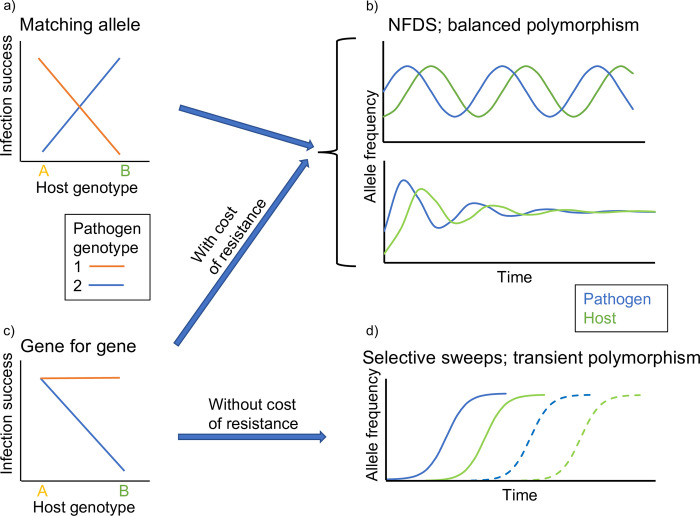
Fig 1. Coevolutionary consequences of different types of G×G.

For simplicity, the figure illustrates a scenario where both host and pathogen are haploid and where the G×G involves 1 host locus and 1 pathogen locus (each with 2 different alleles). In MA models, there is a G×G such that different pathogen genotypes infect different host genotypes (a). MA models readily lead to NFDS and the long-term maintenance of polymorphism at interacting loci in both host and pathogen, either in the form of cyclic allele frequencies or a stable polymorphism (b). This occurs because resistance to 1 pathogen genotype comes with a cost in the form of susceptibility to other pathogen genotypes. In other words, under the MA scenario, there is a trade-off between resistance to different pathogen genotypes. In GFG models, there is a G×G such that some pathogen genotypes infect a wider range of genotypes than others (c). In the basic GFG scenario, there is no cost of host resistance or pathogen infectivity. When a host allele that improves resistance without any costs (to the host) occurs in a population, it will be favoured by selection and driven to fixation. Similarly, when a pathogen allele that improves infectivity without costs (to the pathogen) occurs, it will go to fixation. GFG models without costs of resistance or infectivity therefore lead to selective sweeps with only brief, transient polymorphisms, often referred to as arms race coevolution ((d); note that successive sweeps often occur at different sites in the genome, as indicated by different types of lines). However, if there is a cost of host resistance in the currency of another trait related to fitness so that no host genotype has highest fitness under all conditions (and a cost of pathogen infectivity so that no pathogen genotype has highest fitness under all conditions), also GFG models can lead to coevolution by NFDS and the long-term maintenance of polymorphism in the same way as matching allele models (b) [12]. Note that different types of molecular interactions between host and pathogen can result in both MA and GFG type G×G (see [11]). Whether NFDS results in cycles or stable polymorphism (b) depends on the relative importance of 2 different types of NFDS; direct NFDS (where the fitness of an allele is negatively correlated with its frequency) and indirect NFDS (where the fitness of an allele in the host is negatively correlated with the frequency of an allele at the locus involved in G×G in the coevolving pathogen) [10]. Based on figures in [4,11]. GFG, gene-for-gene; G×G, host genotype-by-pathogen genotype interaction; MA, matching allele; NFDS, negative frequency-dependent selection.