The minimal FLASH sparing effect needed to compensate the increase of radiobiological damage due to hypofractionation for late‐reacting tissues

Abstract

Purpose

Normal tissue (NT) sparing by ultra‐high dose rate (UHDR) irradiations compared to conventional dose rate (CONV) irradiations while being isotoxic to the tumor has been termed “FLASH effect” and has been observed when large doses per fraction (d ≳ 5 Gy) have been delivered. Since hypofractionated treatment schedules are known to increase toxicities of late‐reacting tissues compared to normofractionated schedules for many clinical scenarios at CONV dose rates, we developed a formalism based on the biologically effective dose (BED) to assess the minimum magnitude of the FLASH effect needed to compensate the loss of late‐reacting NT sparing when reducing the number of fractions compared to a normofractionated CONV treatment schedule while remaining isoeffective to the tumor.

Methods

By requiring the same BED for the tumor, we derived the “break‐even NT sparing weighting factor” W _BE for the linear‐quadratic (LQ) and LQ‐linear (LQ‐L) models for an NT region irradiated at a relative dose r (relative to the prescribed dose per fraction d to the tumor). W _BE was evaluated numerically for multiple values of d and r, and for different tumor and NT α/β‐ratios. W _BE was compared against currently available experimental data on the magnitude of the NT sparing provided by the FLASH effect for single fraction doses.

Results

For many clinically relevant scenarios, W _BE decreases steeply initially for d > 2 Gy for late‐reacting tissues with (α/β)_NT ≈ 3 Gy, implying that a significant NT sparing by the FLASH effect (between 15% and 30%) is required to counteract the increased radiobiological damage experienced by late‐reacting NT for hypofractionated treatments with d < 10 Gy compared to normofractionated treatments that are equieffective to the tumor. When using the LQ model with generic α/β‐ratios for tumor and late‐reacting NT of (α/β)_T = 10 Gy and (α/β)_NT = 3 Gy, respectively, most currently available experimental evidence about the magnitude of NT sparing by the FLASH effect suggests no net NT sparing benefit for hypofractionated FLASH radiotherapy (RT) in the high‐dose region when compared with W _BE. Instead, clinical indications with more similar α/β‐ratios of the tumor and dose‐limiting NT toxicities [i.e., (α/β)_T ≈ (α/β)_NT], such as prostate treatments, are generally less penalized by hypofractionated treatments and need consequently smaller magnitudes of NT sparing by the FLASH effect to achieve a net benefit. For strongly hypofractionated treatments (>10–15 Gy/fraction), the LQ‐L model predicts, unlike the LQ model, a larger W _BE suggesting a possible benefit of strongly hypofractionated FLASH RT, even for generic α/β‐ratios of (α/β)_T = 10 Gy and (α/β)_NT = 3 Gy. However, knowledge on the isoeffect scaling for high doses per fraction (≳10 Gy/fraction) and its modeling is currently limited and impedes accurate and reliable predictions for such strongly hypofractionated treatments.

Conclusions

We developed a formalism that quantifies the minimal NT sparing by the FLASH effect needed to compensate for hypofractionation, based on the LQ and LQ‐L models. For a given hypofractionated UHDR treatment scenario and magnitude of the FLASH effect, the formalism predicts if a net NT sparing benefit is expected compared to a respective normofractionated CONV treatment.

1. INTRODUCTION

From early days, although researchers and clinicians have sought to use single or few fraction radiotherapy (RT) to maximize the effect of radiation on tumors, these techniques have effectively often led to an unacceptable excess of late normal tissue (NT) toxicity, requiring more fractionated treatment schedules with smaller doses per fraction d. ¹ To date, clinical treatment schedules predominantly use fractionated treatment schemes with about 2 Gy per fraction, hereafter referred to as normofractionated treatments, because they were often shown to increase the therapeutic ratio by reducing radiobiological damage to late‐reacting NT while still effectively targeting early‐responding tumors. ² , ³ However, the advent of modern RT techniques administering highly targeted and conformal treatments with accurate and steep dose fall‐offs, thereby reducing damage to critical NT effectively, ⁴ , ⁵ , ⁶ means that the number of clinical indications that benefit from hypofractionated treatment schedules has considerably increased. Fractionated treatment regimens and geometric sparing through the delivery of highly targeted conformal dose distributions are the two main methods used by modern RT to reduce damage to NT, hereafter referred to as “NT sparing.”

The use of ultra‐high dose rate (UHDR) irradiations delivered in milliseconds or less, compared to conventional dose rate (CONV) irradiations delivered in minutes, is a promising emerging third method to spare NTs without compromising tumor control. This phenomenon has been termed “FLASH effect” and has been observed for large fraction doses (≳5 Gy) administered in short overall treatment durations (≲0.2 s). ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ Because the FLASH effect may result in complementary NT sparing, it has the potential to improve the therapeutic ratio of RT further, when used in synergy with the two classical NT sparing methods. ⁷ , ⁹ , ¹² The NT sparing by the FLASH effect alone can be quantified by the ratio of CONV dose and UHDR dose to achieve an isoeffect; hereafter, referred to as FLASH modifying factor [FMF = (CONV dose)/(UHDR dose)|_isoeffect]. ¹⁴ To date, most in vivo experiments required single fraction doses d above 5–10 Gy and well beyond to demonstrate a substantial NT sparing effect of UHDR compared to CONV irradiations and it has been found that NT sparing of UHDR compared to CONV irradiations generally increases with increasing the single fraction dose (i.e., FMF decreases). ⁷ , ¹⁴ This suggests that the FLASH effect may be suited to improve the therapeutic ratio of strongly hypofractionated and ablative single fraction treatments and could increase the range of clinical indications that can be treated with such fractionation regimens.

The FLASH effect has been observed for large single fraction doses and some hypofractionated schedules with $d\gg 2\mathrm{Gy}$, ⁷ , ¹³ , ¹⁴ and it is well known that hypofractionated schedules, which are isoeffective for the tumor, often increase toxicities in critical late‐reacting NT. ³ , ¹⁵ Therefore, as long as no substantial FLASH NT sparing for normofractionated schedules can be demonstrated for clinically relevant scenarios, a potential issue for a clinical transfer of the FLASH effect is that for many clinical scenarios, a normofractionated CONV treatment scheme may result in a better clinical outcome than a hypofractionated FLASH treatment, in case the FLASH effect is not compensating for any increase in radiobiological damage to critical late‐reacting NT for the hypofractionated treatment schedule.

To address this question, this work develops a formalism to compute the change in radiobiological damage of NT achieved when shifting from a hypofractionated CONV treatment to a normofractionated CONV treatment and derives the break‐even value of FMF that would be needed to be achieved by a hypofractionated FLASH treatment to compensate this change (see Figure 1). Hereafter, this break‐even value of FMF is referred to as “break‐even NT sparing weighting factor” W _BE. We utilize the biologically effective dose (BED) formalism based on the linear‐quadratic (LQ) and LQ‐linear (LQ‐L) models ² , ¹⁶ , ¹⁷ , ¹⁸ to shift from a normofractionated CONV treatment schedule to a hypofractionated CONV treatment that is equieffective for the tumor and to quantify the respective change of radiobiological damage for NTs (Figure 1, Conversion 1). We derive then W _BE, that is, the FMF value that is needed for the hypofractionated schedule to counteract the change radiobiological damage to NTs, in order to remain also equieffective for the NT (Figure 1, Conversion 2). In a second step, we compare the magnitude of W _BE, derived using the formalism, for different therapeutic scenarios to magnitudes of experimentally derived FMF. This assesses in how far available experimental evidence was able to demonstrate an amplitude of NT sparing by the FLASH effect for large single dose fractions that is superior to NT sparing that would be achieved by delivering a normofractionated CONV treatment.

FIGURE 1.

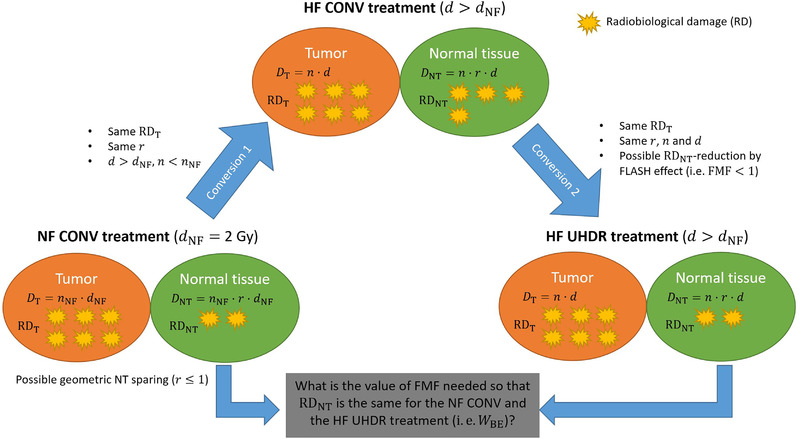
Diagram illustrating the principal research question addressed in this work. For hypofractionated (HF) ultra‐high dose rate (UHDR) radiotherapy (RT) to be favorable compared to normofractionated (NF) conventional dose rate (CONV) RT with the same relative dose distribution (i.e., the same geometric sparing r), the FLASH effect needs to reduce radiobiological damage (RD) to critical normal tissue (NT) regions more than a NF CONV treatment would do. This minimum RD reduction is quantified in this work by the “break‐even NT sparing weighting factor” W _BE and is obtained by requiring that RD to the tumor (T) and the NT are the same for the NF CONV treatment and the HF UHDR treatment. Symbols are defined in Table 1.

2. MATERIALS AND METHODS

2.1. BED and EQD for LQ model

BED and the related equivalent total dose (EQD) are a well‐established formalism with a widespread day‐to‐day clinical use for comparing different fractionation regimens in terms of their tumor control probability and expected NT toxicities. ² , ¹⁶ , ¹⁸ Using the LQ model, BED of a given treatment schedule of n fractions with d dose per fraction is given by

$$\mathrm{BE}{\mathrm{D}}_{\alpha /\beta }\equiv \mathrm{BED}(n,d,\alpha /\beta )=n\times d\left(1+\frac{d}{\alpha /\beta }\right),$$ (1)

where α/β is the α/β‐ratio of the respective tumor or NT. ² The EQD ($\mathrm{EQD}{d}_{\alpha /\beta }^{\prime }$) is then defined by

$$\begin{array}{ccc}\hfill \mathrm{EQD}{d}_{\alpha /\beta }^{\prime }& \equiv & \mathrm{EQD}(n,d,d^{\prime },\alpha /\beta )=n\times d\frac{\left(1+\frac{d}{\alpha /\beta }\right)}{\left(1+\frac{d^{\prime }}{\alpha /\beta }\right)}\hfill \\ & =& n\times d\frac{d+\alpha /\beta }{d^{\prime }+\alpha /\beta }=n^{\prime }\times d^{\prime },\hfill \end{array}$$ (2)

where $n^{\prime }\times d^{\prime }$ corresponds to $\mathrm{EQD}{d}_{\alpha /\beta }^{\prime }$, if the total dose would be given with a dose per fraction dʹ in nʹ fractions (see Table 1).

TABLE 1.

Overview of quantities and their definitions as used in this work

Quantity	Definition/description	Unit
d	Dose per fraction.	Gy
n	Number of fractions.	1
r	Relative dose to a normal tissue region or “geometric sparing”. Expressed as the ratio of dose received by the normal tissue region compared to dose received by the tumor. For instance, a tissue region with $r=0.6$ receives 60% of the dose administered to the tumor, that is, it is spared by 40% (in terms of dose).	1
RD	Radiobiological damage. The minimal FLASH sparing effect needed to compensate the increase of radiobiological damage due to hypofractionation for late‐reacting tissues. BED and EQD are used in this work as a measure of RD to define equieffective treatment schedules for a specific clinical (biological) endpoint. 18	–
FMF	The FMF is defined as the ratio of CONV dose ${(n\times d)}_{\mathrm{CONV}}$ and UHDR dose ${(n\times d)}_{\mathrm{UHDR}}$ to achieve an isoeffect for a given endpoint and for the same number of fractions n, that is: $\mathrm{FMF}=\frac{{(n\times d)}_{\mathrm{CONV}}}{{(n\times d)}_{\mathrm{UHDR}}}{|}_{\mathrm{isoeffect}}=\frac{d_{\mathrm{CONV}}}{d_{\mathrm{UHDR}}}{|}_{\mathrm{isoeffect}}$. 14 For instance, if FMF = 0.7 for a given normal tissue and endpoint, then the UHDR treatment schedule results in a normal tissue sparing of 30% (in terms of dose) compared to a CONV treatment schedule with the same number of fractions n. Per definition, d CONV is then 30% smaller than d UHDR to achieve the same effect.	1
W BE	The “break‐even normal tissue sparing weighting factor” is the value of FMF obtained by requiring that radiobiological damage to the tumor and a given normal tissue region with a geometric sparing of r are the same (i.e., an isoeffect for a given endpoint) for a normofractionated CONV treatment and a hypofractionated UHDR treatment that have the same relative dose distribution (that is, the same r for any given normal tissue region) (see Equation 6 and Supporting Information). For instance, for a normal tissue region that is geometrically spared by $r=0.6$, if $W_{\mathrm{BE}}=0.7$ for a hypofractionated UHDR treatment with $d=10\mathrm{Gy}$ then an FMF smaller than 0.7 (i.e., $\mathrm{FMF}<W_{\mathrm{BE}}$) needs to be achieved by this treatment in order to result in less radiobiological damage to the normal tissue region compared to a normofractionated CONV treatment with $d_{\mathrm{NF}}=2\mathrm{Gy}$ that is isoeffective to the tumor.	1
D BE	The W BE‐weighted dose (see Equation 3).	Gy
$\mathrm{BE}{\mathrm{D}}_{\alpha /\beta }$	For an endpoint with a given α/β‐ratio, BED is defined as “the total absorbed dose that is delivered when the reference treatment plan is conducted with an absorbed dose per fraction approaching 0 Gy” 18 (see Equations 1 and 7).	Gy
$\mathrm{EQD}{d}_{\alpha /\beta }^{\prime }$	For an endpoint with a given α/β‐ratio, the equivalent total dose or equieffective dose (EQD) is defined as “the total absorbed dose delivered by the reference treatment plan (of fraction size dʹ) that leads to the same biological effect as a test treatment plan that is conducted with absorbed dose per fraction d and total absorbed dose” $n\times d$ 18 (see Equation 2).	Gy
α/β	α/β‐ratio of the LQ or the LQ‐L model. α/β is defined as “an endpoint‐ and radiation quality‐specific parameter that describes the effect of changes in dose per fraction” d. 18	Gy
d T	LQ‐L model threshold parameter that defines the onset of the linear response region at high doses. In this work, it is approximated as $d_{\mathrm{T}}=2(\alpha /\beta )$. 17	Gy
$\gamma /\alpha$	LQ‐L model parameter defining the slope at d T. In this work, a continuous derivative at d T is required resulting in $\gamma /\alpha =1+(2d_{\mathrm{T}}/(\alpha /\beta ))$. 17	1

Note: Symbols with the subscript T or NT indicate that the symbol refers to a tumor or normal tissue region, respectively, if not defined explicitly differently. Symbols with the subscript NF indicate that the symbol refers to a normofractionated treatment with $d_{\mathrm{NF}}=2\mathrm{Gy}$.

Abbreviations: BED, biologically effective dose; CONV, conventional dose rate; EQD, equivalent total dose; FMF, FLASH modifying factor; RD, radiobiological damage; UHDR, ultra‐high dose rate.

2.2. Definition of W _BE and illustrative example calculations

We define the “break‐even NT sparing weighting factor” W _BE for an NT region at the relative dose level r of the prescribed dose to be the NT sparing factor required to compensate the change in radiobiological damage of the NT for a hypofractionated treatment compared to a normofractionated treatment that is equieffective for the tumor (see Figure 1 and Table 1). W _BE follows the same concept as the break‐even isodose level for hypofractionated CONV treatments. ¹⁵ , ¹⁹ Its principle is illustrated by the following example calculations.

Consider a normofractionated CONV treatment of 30 × 2 Gy (i.e., n _NF = 30, d _NF = 2 Gy) and assume α/β‐ratios of ${(\alpha /\beta )}_{\mathrm{T}}=10\mathrm{Gy}$ and ${(\alpha /\beta )}_{\mathrm{NT}}=3\mathrm{Gy}$ for tumor and late‐reacting NT, respectively (hereafter referred to as “generic α/β‐ratios”). Such a treatment administers a BED₁₀ of (Equation 1) $30\times 2\mathrm{Gy}(1+\frac{2\mathrm{Gy}}{10\mathrm{Gy}})=72\mathrm{Gy}$ to the tumor. Suppose that the dose would be administered with a dose per fraction dʹ of 6.4 Gy, then the EQD for NT receiving 100% of the total prescribed dose is given by (Equation 2) $\mathrm{EQD}6.4_3=30\times 2\mathrm{Gy}\frac{2\mathrm{Gy}+3\mathrm{Gy}}{6.4\mathrm{Gy}+3\mathrm{Gy}}\approx 31.9\mathrm{Gy}$. Instead, if we intend to administer an equieffective treatment of $\mathrm{BE}{\mathrm{D}}_{10}=72\mathrm{Gy}$ to the tumor with d = 8 Gy, we need to deliver five fractions, since $\mathrm{BE}{\mathrm{D}}_{10}=5\times 8\mathrm{Gy}(1+\frac{8\mathrm{Gy}}{10\mathrm{Gy}})=72\mathrm{Gy}$. In order to obtain an isoeffect for late NT reactions with this treatment, we need an EQD of $\mathrm{EQD}{d}_3^{\prime }=31.9\mathrm{Gy}=5\times d^{\prime }$ with $d^{\prime }=W_{\mathrm{BE}}\times 8\mathrm{Gy}$ and an NT sparing weighting factor W _BE of ≈0.80. Then, $d^{\prime }=0.80\times 8\mathrm{Gy}=6.4\mathrm{Gy}$ and hence $\mathrm{EQD}6.4_3=5\times 0.80\times 8\mathrm{Gy}\approx 31.9\mathrm{Gy}$, that is, the same as for the normofractionated CONV treatment schedule.

Consider now the same normofractionated CONV treatment schedule for an NT region that does not receive the full prescribed dose, but only 50% of the prescribed dose (r = 0.5). The EQD for such NT volume is $\mathrm{EQD}3.6_3=30\times 0.5\times 2\mathrm{Gy}\frac{0.5\times 2\mathrm{Gy}+3\mathrm{Gy}}{3.6\mathrm{Gy}+3\mathrm{Gy}}\approx 18.1\mathrm{Gy}$ with a dose per fraction to the NT of $d^{\prime }=0.5\times 7.2\mathrm{Gy}=3.6\mathrm{Gy}$. To obtain an isoeffect for the NT region at $r=0.5$ with the hypofractionated treatment schedule of 5 × 8 Gy, we need an EQD of $\mathrm{EQD}{d}_3^{\prime }=18.1\mathrm{Gy}=5\times d^{\prime }$ with $d^{\prime }=W_{\mathrm{BE}}\times r\times 8\mathrm{Gy}$ and $W_{\mathrm{BE}}\approx 0.91$. Since then $d^{\prime }=0.91\times 0.5\times 8\mathrm{Gy}\approx 3.6\mathrm{Gy}$ and hence $\mathrm{EQD}3.6_3=5\times 0.91\times 0.5\times 8\mathrm{Gy}\approx 18.1\mathrm{Gy}$. Note that all approximate signs for the calculations above are due to rounding.

2.3. Formalism assumptions and derivation of W _BE for the LQ model

To generalize the calculation examples of the previous section, we derive W _BE for a hypofractionated treatment schedule $(n,d)$ so that it is isoeffective both for the tumor and for an NT region that receives a relative dose r of the prescribed dose per fraction d, when compared to a normofractionated reference treatment schedule $(n_{\mathrm{NF}},d_{\mathrm{NF}})$, where $d_{\mathrm{NF}}=2\mathrm{Gy}$. Isoeffectiveness is quantified here by iso‐BED for the tumor and by iso‐EQD for the NT, where tumor and NT are characterized by (α/β)_T and (α/β)_NT, respectively. We used iso‐EQD for NT irradiated by CONV, rather than applying iso‐BED for NT irradiated by UHDR, to avoid applying the BED formalism to NT that may experience the FLASH effect. This is done because isoeffective dose scaling between different fractionation schedules may be altered for NT experiencing the FLASH effect and, consequently, the BED formalism and the CONV (α/β)_NT‐ratio may no longer be valid (see also assumption 3 below). The following assumptions are made for the derivation:

1. The normofractionated $(n_{\mathrm{NF}},d_{\mathrm{NF}})$ and the hypofractionated $(n,d)$ treatment schedules have the same relative dose distribution, that is, their total dose distributions differ only by a single total dose scaling factor given by $(n\times d)/(n_{\mathrm{NF}}\times d_{\mathrm{NF}})$ and they provide the same geometric sparing r.

2. For a hypofractionated treatment schedule $(n,d)$ delivered with UHDR, there may be an NT sparing effect but the effect on the tumor irradiated by UHDR is unaltered compared to a CONV schedule with $(n,d)$. That is, we assume an isoefficacy of UHDR irradiation for tumors compared to CONV irradiation for the same dose d, as suggested by multiple studies ⁷ , ²⁰ (see Section 4 for limitations of this assumption). Since the effect on the tumor is unaltered, we assume also that the BED formula (Equation 1) and the respective (α/β)_T apply equally for CONV and UHDR irradiation to determine equieffective treatment schedules for the tumor, that is, schedules with the same BED.

3. Furthermore, we assume that the EQD formula (Equation 2) can be used to obtain the isoeffect for an NT region with (α/β)_NT for a differently fractionated treatment with a dose per fraction dʹ in terms of EQD $\mathrm{EQD}{d}_{{(\alpha /\beta )}_{\mathrm{NT}}}^{\prime }$ for CONV irradiation. Note that no assumption is made at this point on the isoeffect scaling between different fractionation schemes for NT irradiated with UHDR, which may experience an NT sparing FLASH effect. That is, the LQ model (and the associated (α/β)_NT) is not used to perform isoeffect scaling between treatment regimens for NT experiencing the FLASH effect. Instead, for a given hypofractionated UHDR treatment schedule $(n,d)$, all changes in radiobiological damage that occur due to NT sparing by the FLASH effect compared to a hypofractionated CONV treatment are incorporated in the FMF for the treatment. With W _BE, our formalism establishes an isoeffect threshold for this FMF.

Note that using the formalism, the LQ model is only used for isoeffect scaling between different treatment regimens for tumor and NTs that do not experience a FLASH effect. Hence, the same assumptions are valid as when employing the LQ model for isoeffect scaling of CONV treatment regimen, which is common practice in clinical routine and leads to clinically acceptable results. ² , ¹⁶ , ¹⁸

W _BE is defined as the dose‐weighting factor needed for a given (single or multi‐fraction) hypofractionated treatment $(n,d)$ to achieve the same NT sparing as the corresponding normofractionated treatment schedule $(n_{\mathrm{NF}},d_{\mathrm{NF}})$ for a given tissue region at r. Hence, the total W _BE‐weighted dose D _BE of the hypofractionated schedule given with a dose per fraction r × d in n fractions (Equation 2, right‐hand‐side) is given by multiplying n × r × d with the dose‐weighting factor W _BE

$$D_{\mathrm{BE}}\equiv D_{\mathrm{BE}}(W_{\mathrm{BE}},n,r,d)=n\times W_{\mathrm{BE}}\times r\times d.$$ (3)

By requiring that D _BE be equal to the EQD $\mathrm{EQD}(n_{\mathrm{NF}},r\times d_{\mathrm{NF}},W_{\mathrm{BE}}\times r\times d,{(\alpha /\beta )}_{\mathrm{NT}})$ (Equation 2, left‐hand‐side) of a respective normofractionated treatment, W _BE can then be derived for a hypofractionated treatment with the same BED to the tumor as follows. For schedules $(n_{\mathrm{NF}},d_{\mathrm{NF}})$ and $(n,d)$, an isoeffect for the tumor and an isoeffect for an NT at relative dose level r is given by requiring:

$$\mathrm{BED}\left(n_{\mathrm{NF}},d_{\mathrm{NF}},{(\alpha /\beta )}_{\mathrm{T}}\right)=\mathrm{BED}\left(n,d,{(\alpha /\beta )}_{\mathrm{T}}\right),$$ (4)

$$\begin{array}{ccc}& & \mathrm{EQD}\left(n_{\mathrm{NF}},r\times d_{\mathrm{NF}},W_{\mathrm{BE}}\times r\times d,{(\alpha /\beta )}_{\mathrm{NT}}\right)\hfill \\ & & =D_{\mathrm{BE}}(W_{\mathrm{BE}},n,r,d).\hfill \end{array}$$ (5)

By solving the latter condition for W _BE with Equations (2) and (3), and by substituting the first condition while using Equation (1), W _BE can be derived for the LQ model as (see Supporting Information for a detailed derivation):

$$\begin{array}{c}{W}_{\mathrm{BE}}\equiv W_{\mathrm{BE}}(d,r)\equiv W_{\mathrm{BE}}\left(d,r,{(\alpha /\beta )}_{\mathrm{T}},{(\alpha /\beta )}_{\mathrm{NT}},d_{\mathrm{NF}}\right)\hfill \\ =-\frac{{(\alpha /\beta )}_{\mathrm{NT}}}{2rd}+\sqrt{\frac{{(\alpha /\beta )}_{\mathrm{NT}}^2}{4r^2{d}^2}+\left(\frac{{(\alpha /\beta )}_{\mathrm{NT}}}{rd}+\frac{d_{\mathrm{NF}}}{d}\right)\times \frac{d+{(\alpha /\beta )}_{\mathrm{T}}}{d_{\mathrm{NF}}+{(\alpha /\beta )}_{\mathrm{T}}}}.\hfill \end{array}$$ (6)

Note that for this representation, W _BE is independent of the initially chosen number of fractions n _NF and n. Hence, a change in n _NF, n, $\mathrm{BE}{\mathrm{D}}_{{(\alpha /\beta )}_{\mathrm{T}}}$ and total dose will not affect W _BE as long as d and r remain constant. Note also that

1. If $W_{\mathrm{BE}}(d,r)>1$, then NT at r are additionally spared by a hypofractionated schedule with d compared to a normofractionated schedule with d _NF.

2. If $W_{\mathrm{BE}}(d,r)<1$, then NT at r are less spared by a hypofractionated schedule with d compared to a normofractionated schedule with d _NF. The effective dose to the NT at r needs to be reduced for the hypofractionated treatment by the dose‐weighting factor W _BE (by the FLASH effect) to be equieffective to the normofractionated treatment.

3. $W_{\mathrm{BE}}(d,r)=1$ for $r={(\alpha /\beta )}_{\mathrm{NT}}/{(\alpha /\beta )}_{\mathrm{T}}$.

4. $W_{\mathrm{BE}}(d,r)$ is strictly monotonously decreasing as a function of d for$r>{(\alpha /\beta )}_{\mathrm{NT}}/{(\alpha /\beta )}_{\mathrm{T}}$.

5. $W_{\mathrm{BE}}(d,r)$ is strictly monotonously increasing as a function of d for$r<{(\alpha /\beta )}_{\mathrm{NT}}/{(\alpha /\beta )}_{\mathrm{T}}$.

6. $W_{\mathrm{BE}}(d,r)=1$ for $d=d_{\mathrm{NF}}$, by definition.

This behavior is discussed elsewhere in more detail for CONV treatments. ¹⁵

2.4. Derivation of W _BE using LQ‐L

While BED isoeffect scaling of different treatment schedules using the LQ model has a wide spread and successful use in clinical radio‐oncology, the LQ model was shown to have shortcomings in predicting responses for large doses per fraction (≳6–10 Gy). ³ , ⁴ , ¹⁷ , ²¹ , ²² Some experimental data suggest a transition from a quadratic to a linear behavior at such high doses and several models introducing this behavior have been proposed to describe high‐dose data more accurately. ⁴ , ¹⁷ , ²² , ²³ The LQ‐L model is one of these models with an advantage of maintaining a relatively simple functional form. ¹⁷ For the LQ‐L model, BED is given by ¹⁷

$$\mathrm{BED}(n,d,\alpha /\beta ,d_{\mathrm{T}},\gamma /\alpha )=\left\{\begin{array}{cc}n\times d\left(1+\frac{d}{\alpha /\beta }\right)& \mathrm{for}d\le d_{\mathrm{T}}\\ n\left[d_{\mathrm{T}}\left(1+\frac{d_{\mathrm{T}}}{\alpha /\beta }\right)+\frac{\gamma }{\alpha }(d-d_{\mathrm{T}})\right]& \mathrm{for}d>d_{\mathrm{T}}\end{array}\right.,$$ (7)

where d _T is the threshold parameter for the onset of the linear behavior at high doses and γ determines the slope in this region (log_e cell kill per Gy). To evaluate the effect of a transition to a linear behavior, we use this formula to compute W _BE analogous to Equation (6) for the LQ model while making the same assumptions mentioned in the previous section, but this time using the LQ‐L model. The lengthy equations for W _BE derived for the LQ‐L model are provided in Supporting Information. Note that the resulting equations for W _BE are again, as for the LQ model, independent of the initially chosen number of fractions n _NF and n. For the evaluations presented in the following, we required a continuous derivative at d _T, implying that $\gamma /\alpha =1+(2d_{\mathrm{T}}/(\alpha /\beta ))$, and approximated d _T by $2(\alpha /\beta )$, as suggested by Astrahan, ¹⁷ thereby reducing the number of tissue dependent parameters in Equation (7) from three to one, that is, α/β.

2.5. Numerical evaluations of W _BE and comparison to measured FLASH effect normal tissue sparing factors

To assess magnitudes and trends of W _BE as a function of dose per fraction d, we evaluated W _BE based on the LQ and LQ‐L models (see Equation 6 and Supporting Information) using different values of clinical interest for r, (α/β)_T, and (α/β)_NT.

Most currently available experimental evidence of NT sparing by the FLASH effect comes from single fraction animal irradiations. ⁷ , ¹² FMF for various in vivo endpoints derived from single fraction animal irradiations were summarized in a recent study as a function of UHDR dose d. ¹⁴ We compared the amplitude of these single fraction experimental FMF to W _BE as a function of dose per fraction d. Details about the FMF derived from experiments can be found in the corresponding publication. ¹⁴

3. RESULTS

3.1. Numerical evaluation of W _BE

Using generic α/β‐ratios for tumors and late‐reacting NT of (α/β)_T = 10 Gy and (α/β)_NT = 3 Gy, ² respectively, and a normofractionated reference treatment schedule of 30 × 2 Gy results in a set of hypofractionated treatment schedules with an isoeffect to the tumor of $\mathrm{BE}{\mathrm{D}}_{10}=72\mathrm{Gy}$. W _BE values for this set of hypofractionated treatment schedules are displayed in Figure 2 for different geometric sparing factors r using the LQ and LQ‐L models (i.e., Equation 6 and Supporting Information). Figure 2a displays W _BE as a function of UHDR dose per fraction d and Figure 2b displays W _BE as a function of UHDR fraction number n for $\mathrm{BE}{\mathrm{D}}_{10}=72\mathrm{Gy}$. An FMF smaller than W _BE needs to be reached for a hypofractionated UHDR treatment with dose per fraction d, to be advantageous for a tissue region at dose level r, compared to a normofractionated CONV treatment.

FIGURE 2.

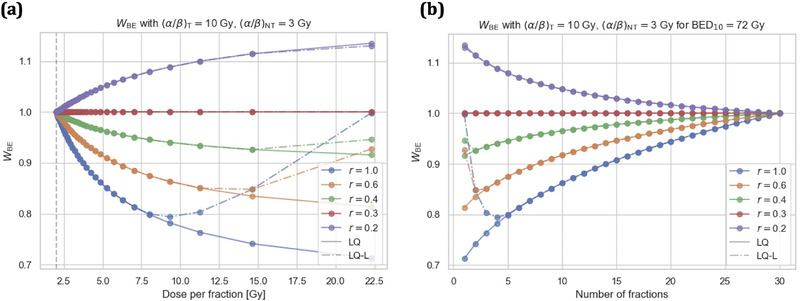
Break‐even normal tissue (NT) sparing factor W _BE as predicted by the linear‐quadratic (LQ) and LQ‐linear (LQ‐L) models for different relative doses levels r as a function of ultra‐high dose rate (UHDR) dose per fraction d (a) and as a function of UHDR fraction number n (b) for a set of hypofractionated treatment schedules with a BED₁₀ of 72 Gy to the tumor. A FLASH modifying factor smaller than W _BE needs to be reached for a hypofractionated UHDR treatment with dose per fraction d, to be advantageous for a tissue region at dose level r, compared to a normofractionated conventional dose rate treatment. The generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy for late‐reacting NT and tumors, respectively, were used for the calculations. Markers indicate integer fraction numbers n for a BED₁₀ of 72 Gy to the tumor. A normofractionated treatment with $d=2\mathrm{Gy}$ is indicated by a gray dashed vertical line.

In Figure 3, W _BE values (i.e., Equation 6 and Supporting Information) are displayed as a function of d for r = 1.0 (left) and r = 0.5 (right) and for different combinations of (α/β)_NT‐ratios (2, 3, 5, and 10 Gy) and (α/β)_T‐ratios (5, 10, and 20 Gy). This allows to assess the sensitivity of W _BE to variations of the tissue‐specific parameters (α/β)_T and (α/β)_NT of the formalism for two different r. Note that for a given treatment schedule and α/β‐ratios, only d and r determine W _BE, since W _BE values do not depend on the fraction number and tumor BED when displayed as a function of d (see Equation 6 and Supporting Information). W _BE values as predicted by the LQ model for (α/β)_NT = 3 Gy as a function of (α/β)_T and for (α/β)_T = 10 Gy as a function of (α/β)_NT are displayed in Figure S1 for different UHDR doses per fraction d (5, 10, 15, and 20 Gy) and for relative dose levels r of 1.0 and 0.5.

FIGURE 3.

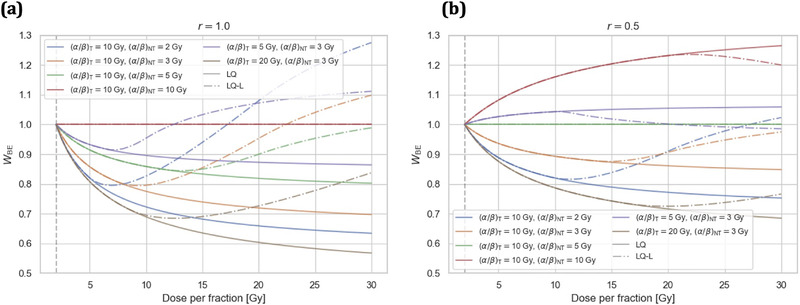
Break‐even normal tissue (NT) sparing factor W _BE as predicted by the linear‐quadratic (LQ) and LQ‐linear (LQ‐L) models as a function of dose per fraction d for relative dose levels r of 1.0 (a) and 0.5 (b). Curves for different combinations of (α/β)_NT‐ratios (2, 3, 5, and 10 Gy) and (α/β)_T‐ratios (5, 10, and 20 Gy) are displayed. A normofractionated treatment with $d=2\mathrm{Gy}$ is indicated by a gray dashed vertical line.

3.2. Comparison of W _BE to experimental FMF data

In Figures 4 and S2, W _BE curves as predicted by the LQ and LQ‐L models (i.e., Equation 6 and Supporting Information) are compared to experimental single fraction FMF as a function of dose per fraction for r = 1.0 and 0.5 using generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy.

FIGURE 4.

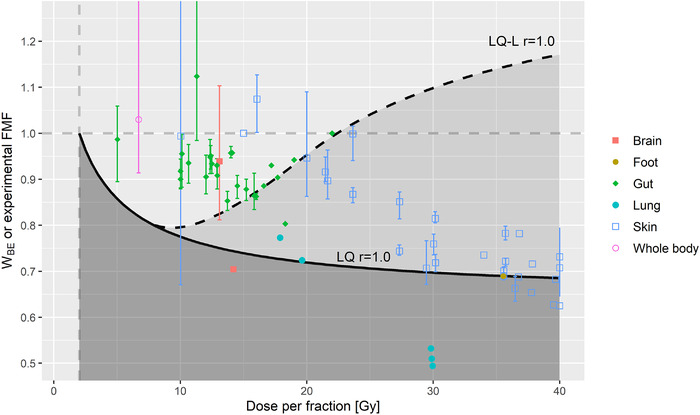
Points display FLASH modifying factors (FMF) for different mammalian organs/body parts derived from single fraction experiments as a function of single fraction ultra‐high dose rate (UHDR) dose (data reproduced from Ref. [14]). Break‐even normal tissue (NT) sparing factors W _BE as a function of dose per fraction to the NT are displayed as predicted by the linear‐quadratic (LQ) (solid lines) and LQ‐linear (LQ‐L) (dashed lines) models for a generic scenario using α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy for late‐reacting NT and the tumor, respectively, and r = 1.0. W _BE values are displayed for a dose per fraction range from 2 to 40 Gy. An FMF smaller than W _BE (i.e., dark‐shaded area for the LQ model and light‐shaded area for the LQ‐L model) needs to be reached by a hypofractionated UHDR treatment with dose per fraction d, to be advantageous for a tissue region at dose level r, compared to a normofractionated conventional dose rate treatment. A normofractionated treatment with $d=2\mathrm{Gy}$ is indicated by a gray dashed vertical line.

4. DISCUSSION

Assuming that FLASH RT is isoeffective for the tumor compared to CONV RT, ⁷ , ¹² the magnitude of the additional NT sparing by the FLASH effect, quantified by FMF, will be a pivotal factor for its clinical success. NT protection by the FLASH effect was observed in vivo for d ≳ 5 Gy and generally increases in magnitude for larger d. ¹⁴ However, for many clinical indications increasing d is known to be more toxic for late‐reacting healthy tissues in the high‐dose region (r ≈ 1.0). Hence, there is potentially an antagonistic behavior between NT sparing by the FLASH effect when using hypofractionated treatment schedules, since such hypofractionated schedules are known to increase toxicities for critical late‐reacting tissues compared to normofractionated schedules that are equieffective for the tumor when delivered with CONV dose rates. With the break‐even NT sparing factor W _BE, we developed a formalism for the quantitative evaluation of this antagonistic behavior based on the LQ and LQ‐L models. For a given clinical scenario and hypothesis about the expected magnitude of the NT sparing by the FLASH effect, the formalism predicts whether a net NT sparing benefit for a given hypofractionated UHDR treatment is expected compared to a respective normofractionated CONV treatment.

An increasing number of clinical indications can be treated with hypofractionated schedules using modern RT techniques, such as stereotactic and intensity‐modulated RT, as they are capable of delivering highly conformal dose distributions that spare critical healthy tissues geometrically (i.e., r < 1) efficiently. ⁴ , ⁵ , ⁶ , ¹⁵ , ¹⁹ Future FLASH RT treatments should ideally retain this dosimetric conformity and further improve the achievable therapeutic ratio by an additional NT sparing (i.e., FMF < 1). In clinical practice, critical toxicities are usually late effects encountered in the high‐dose region inside or in the vicinity of the planning target volume. ³ This makes W _BE values in the high‐dose region (r ≈ 1.0) and for low (α/β)_NT of about 3 Gy clinically the most relevant scenario. For the most commonly encountered clinical situation with late‐reacting NT (α/β)_NT < (α/β)_T and within the validity range of the LQ model, shifting to a more hypofractionated treatment schedule with larger d results in W _BE values smaller than one for the high‐dose region; indicating a worsening of NT sparing. For such hypofractionated treatment schedules, W _BE decreases initially steeply for d > 2 Gy, implying that a significant NT sparing by the FLASH effect is required to counteract the loss in NT sparing compared to the one achieved for a normofractionated treatment. For instance, as illustrated in the initial calculation example using the LQ model, for generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy and a hypofractionated schedule with d = 8 Gy, an NT sparing by the FLASH effect of at least 20% (i.e., FMF ≤ W _BE = 0.80) and 9% (i.e., FMF ≤ W _BE = 0.91) is needed to compensate for tissues at relative dose levels of r = 1.0 and 0.5, respectively. Evaluated W _BE values for the LQ model are in general larger for smaller r, implying that less NT sparing by the FLASH effect is needed to compensate hypofractionation for lower relative dose levels r. W _BE values predicted by the LQ model are also larger for clinical scenarios where tumor and critical late‐reacting NT α/β‐ratios are more similar than the generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy, suggesting that such indications could already profit for smaller magnitudes of NT sparing achieved by the FLASH effect when using hypofractionated UHDR RT. Note in particular, that for early effects it is often assumed that (α/β)_NT = (α/β)_T = 10 Gy, which results in W _BE = 1, and hence no penalty when moving to a hypofractionated treatment. Also for prostate cancer and some other tumors, there is evidence that the tumor (α/β)_T‐ratio is similar to that of late‐reacting NT tissues (i.e., about 3 Gy) ²⁴ and hence no or only small penalties are expected when moving to a hypofractionated treatment for such cases.

Some have argued that the LQ model is experimentally and theoretically reasonably well validated up to about 10 Gy per fraction and is reasonable to use up to about 18 Gy per fraction ²⁵ , ²⁶ while others disagree with that view. ¹⁷ , ²¹ More generally, isoeffect curves for large fraction doses (≳10 Gy) and underlying mechanisms are not yet well modeled. ²¹ , ²⁷ The LQ‐L model belongs to the family of models that predict a linear response behavior at high doses and, compared to the LQ model, such behavior is in better agreement with some experimental findings. ³ , ¹⁷ , ²¹ , ²² For the high‐dose region (r = 1.0), predictions of W _BE obtained by the LQ‐L model show an inverse trend for large d for all combinations of α/β‐ratios evaluated in this work: after reaching a minimum W _BE, W _BE starts to increase again monotonously, sometimes reaching W _BE > 1 (see Figure 3). This behavior is due to the transition from a linear‐quadratic to a linear behavior at d _T and is consistent with results from previous studies for CONV treatments. ¹⁵ , ¹⁷ It suggests that a therapeutically unfavorable intermediate hypofractionation regimen may exist for high‐dose regions (roughly for d between 3 and 15 Gy for the evaluated α/β‐ratios) and that NT sparing may improve again for d beyond this regimen. However, predictions based on the LQ‐L should be interpreted with caution, as it is currently unclear if, and if yes, for which clinical scenarios, they may apply. In particular, the LQ‐L model and its high‐dose parameters d _T and γ/α are not well established and validated for clinical cases. ⁴ , ¹⁷ , ²⁸ More generally, a linear high‐dose behavior has been mostly found by in vitro experiments where there are severe limitations on dose range and increasing statistical uncertainties where the surviving fraction is low due to low surviving colony numbers; it may be therefore be artifactual. In comparison, in vivo experiments involve much greater dose ranges (taken to levels of surviving fractions not found in in vitro work) and are not so reliant on dose limitations. The use of the unaltered LQ model appears to work well for clinical data sets but a linear high‐dose behavior, as modeled by the LQ‐L model, represents an alternative hypothesis. In the context of this work, diverging predictions of W _BE for the LQ and LQ‐L models illustrate persisting uncertainties of isoeffect modeling at large doses per fraction. Furthermore, there are several phenomena, including repopulation, hypoxia, and volume effects, which are not taken into account by the W _BE formalism presented here for both the LQ and LQ‐L models. A more detailed discussion of these aspects can be found elsewhere. ³ , ⁴ , ¹⁵

Comparing the magnitude of W _BE to experimental evidence about the magnitude of NT sparing by the FLASH effect for a given d and α/β‐ratios makes it possible to assess if there is a net benefit predicted by the presented formalism. The comparison of W _BE obtained with the LQ model for generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy and r = 1.0 to FMF from single fraction experiments presented in Figure 4 shows that the magnitude of most FMF is larger than W _BE for d < 30 Gy. This implies that currently most of the performed mammalian NT studies achieved an NT sparing by FLASH for large single doses that is not sufficient to outperform the NT sparing obtained by a normofractionated CONV treatment as predicted by the LQ model for the generic α/β‐ratios and r = 1.0, but some experimental FMF demonstrate that in principle magnitudes similar to W _BE can be reached, at least for specific tissues and endpoints. Instead, for predictions of W _BE using the LQ‐L model with generic α/β‐ratios of (α/β)_NT = 3 Gy and (α/β)_T = 10 Gy, W _BE increases again beyond a d of 8 Gy, and magnitudes of experimental FMF suggest that there could be a net benefit for d > 10–15 Gy. In this regard, it should also be kept in mind that if an acceptable clinical outcome can be achieved, the associated socio‐economic benefits may support delivering an accelerated hypofractionated treatment schedule for some clinical indications, therefore increasing the number of cases that can be treated with hypofractionated RT. ⁴ Furthermore, the FLASH effect may of course also increase the clinical benefit for treatments that are already currently delivered using hypofractionated schedules. A recent randomized phase III trial treated nasal squamous cell carcinoma of cat patients with FLASH RT (1 × 30 Gy) and standard‐of‐care CONV RT (10 × 4.8 Gy) and reported comparable local control, overall survival time, and comparable acute toxicities, but resulted in severe late toxicities for the FLASH RT arm (3 of 7 cats with maxillary bone necrosis 9–15 months after FLASH RT versus 0 of 9 for CONV RT), which led to a premature interruption of the trial. ²⁹ The trial results underline the need for caution when delivering hypofractionated FLASH RT schedules. However, since FLASH RT arm and CONV RT arm schedules have a very different tumor BED, it is difficult to interpret the obtained results in the context of the present formalism.

Experimental FMF to which W _BE is compared here come from single dose irradiations of small volumes (using field sizes of 2–4 cm at most) of different mammalian biological systems, endpoints, and effect assessment times (spanning days to years). ¹⁴ It is currently largely unclear how these factors influence the magnitude of FMF. In particular, it is not established if, and if yes, how FMF change for multi‐fractionated UHDR irradiations. A recent study demonstrated the existence of an NT sparing effect for fractionated UHDR compared to CONV irradiations in the murine brain. ¹³ However, it is difficult to extract any quantitative information on the behavior of FMF for different fractionation schemes from the study, which is useful in the context of this work. Furthermore, the FMF values presented in Figure 4 were obtained mostly from initial preclinical animal experiments, which were focused on demonstrating the existence of a FLASH effect. Hence, experimental conditions can often be considered suboptimal for achieving a maximum FLASH effect and there are likely systematic differences of these data compared to FMF values potentially achievable for therapeutic scenarios. Another noteworthy point is that while we assumed for this work that UHDR RT is isoeffective for tumors compared to CONV RT, as suggested to date by most in vivo antitumor efficacy studies comparing UHDR and CONV irradiation, ⁷ , ²⁰ there is some emerging evidence that this may not always be the case. For instance, a recent study found UHDR irradiations to be more effective for hypoxic tumors compared to CONV irradiations. ³⁰ Another recent study found UHDR carbon ion irradiations to be more effective in a murine osteosarcoma model. ³¹ Such a behavior may be an additional asset for FLASH RT, which is not considered in this work and the current version of the formalism. This work focuses on the development of the formalism and an analysis of the antagonistic effects for generic scenarios. For specific clinical scenarios, more detailed considerations are required, likely involving exemplary patient cases and delivery techniques, as well as more specific measurements or predictions of FMF for the individual scenario and thresholds for relevant NT complications. Such considerations should ideally also encompass an assessment of uncertainties of different parameters entering the comparison and an evaluation of their impact on W _BE and FMF.

Previous work ¹⁵ evaluated changes of NT sparing between normofractionated and hypofractionated CONV RT (see “Conversion 1” of Figure 1) and quantified these changes using the ratio of hypofractionated and normofractionated NT BED, that is, BED_IET. The present work extends the previous formalism by incorporating a possible NT sparing by the FLASH effect and by predicting a required FMF for the same NT sparing, that is, W _BE (see “Conversion 2” of Figure 1). Moreover, it compares W _BE to experimental FMF. While both BED_IET and W _BE exhibit similar behaviors, they differ in amplitude.

5. CONCLUSIONS

Based on the LQ and LQ‐L models, we developed a formalism to evaluate the antagonistic effects of the loss of late‐reacting NT sparing when shifting to a hypofractionated treatment schedule against the potentially increased NT sparing by the FLASH effect for such a hypofractionated treatment using the concept of the “break‐even NT sparing weighting factor” W _BE. When shifting from a normofractionated to a hypofractionated treatment, a steep initial loss of NT sparing is predicted in the high‐dose region for many clinically relevant scenarios for late‐reacting NT. For clinical situations with generic α/β‐ratios of (α/β)_NT = 3 Gy for late‐reacting NT and (α/β)_T = 10 Gy for the tumor where the LQ model is applicable, most currently available experimental evidence about the magnitude of NT sparing by the FLASH effect suggests no net sparing benefit for hypofractionated FLASH RT in the high‐dose region, but a few studies show NT sparing magnitudes which are comparable. Instead, clinical indications with similar α/β‐ratios are generally less penalized by hypofractionated treatments and the present analysis suggests that they could profit in some cases from enhanced NT sparing by hypofractionated FLASH RT. For strongly hypofractionated treatments (>10–15 Gy/fraction) the LQ‐L model predicts, unlike the LQ model, an increasing W _BE which suggests a possible benefit of strongly hypofractionated FLASH RT, even for generic α/β‐ratios.

ACKOWLEDGMENTS

This research has been partially funded by the ISREC Foundation thanks to a Biltema donation and by the Fondation pour le soutien de la recherche et du developpement de l'oncologie (FSRDO).

Open access funding provided by Universite de Lausanne.

CONFLICT OF INTEREST

The authors declare they have no conflicts of interest.

Supporting information

Supplementary Material

Böhlen TT, Germond J‐F, Bourhis J, Bailat C, Bochud F, Moeckli R. The minimal FLASH sparing effect needed to compensate the increase of radiobiological damage due to hypofractionation for late‐reacting tissues. Med Phys. 2022;49:7672–7682. 10.1002/mp.15911

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.