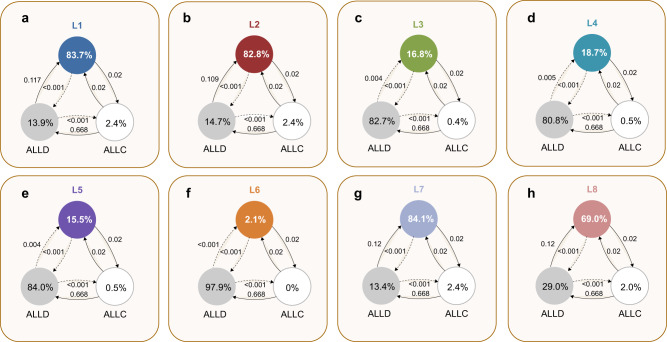
Fig. 5. Evolution of the leading eight with quantitative assessment.

We show the results of simulating evolutionary dynamics when players can choose among three different norms: a leading eight norm, ALLC, and ALLD. We assume that the spread of social norms is described by a pairwise comparison process⁵⁴, such that norms of players with high payoffs are more likely to be successful. Here, we use the limit of rare mutations, such that populations are homogeneous most of the time^57,58,85. Numbers in circles show how often each social norm is adopted on average. Arrows indicate fixation probabilities, i.e., how likely it is for other social norms to invade a given resident population. Solid arrows indicate that the respective transition is more likely to occur than expected under neutrality, whereas dotted arrows indicate that the respective transition is comparably unlikely. We see that four of the eight considered norms, L1 (a), L2 (b), L7 (g), and L8 (h) achieve high abundance in equilibrium, with L1, L2, and L7 played over 80% of the time. The remaining four norms, L3 (c), L4 (d), L5 (e), L6 (f) do not evolve in large proportions, and the respective dynamics strongly favor ALLD. Parameters: R = 5, S = 0, N = 50, ε = 0.05, b = 5, c = 1, q = 0.9, using a strength of selection of s = 1.