Abstract
Background
We reported the concept of patient‐specific deep learning (DL) for real‐time markerless tumor segmentation in image‐guided radiotherapy (IGRT). The method was aimed to control the attention of convolutional neural networks (CNNs) by artificial differences in co‐occurrence probability (CoOCP) in training datasets, that is, focusing CNN attention on soft tissues while ignoring bones. However, the effectiveness of this attention‐based data augmentation has not been confirmed by explainable techniques. Furthermore, compared to reasonable ground truths, the feasibility of tumor segmentation in clinical kilovolt (kV) X‐ray fluoroscopic (XF) images has not been confirmed.
Purpose
The first aim of this paper was to present evidence that the proposed method provides an explanation and control of DL behavior. The second purpose was to validate the real‐time lung tumor segmentation in clinical kV XF images for IGRT.
Methods
This retrospective study included 10 patients with lung cancer. Patient‐specific and XF angle‐specific image pairs comprising digitally reconstructed radiographs (DRRs) and projected‐clinical‐target‐volume (pCTV) images were calculated from four‐dimensional computer tomographic data and treatment planning information. The training datasets were primarily augmented by random overlay (RO) and noise injection (NI): RO aims to differentiate positional CoOCP in soft tissues and bones, and NI aims to make a difference in the frequency of occurrence of local and global image features. The CNNs for each patient‐and‐angle were automatically optimized in the DL training stage to transform the training DRRs into pCTV images. In the inference stage, the trained CNNs transformed the test XF images into pCTV images, thus identifying target positions and shapes.
Results
The visual analysis of DL attention heatmaps for a test image demonstrated that our method focused CNN attention on soft tissue and global image features rather than bones and local features. The processing time for each patient‐and‐angle‐specific dataset in the training stage was ∼30 min, whereas that in the inference stage was 8 ms/frame. The estimated three‐dimensional 95 percentile tracking error, Jaccard index, and Hausdorff distance for 10 patients were 1.3–3.9 mm, 0.85–0.94, and 0.6–4.9 mm, respectively.
Conclusions
The proposed attention‐based data augmentation with both RO and NI made the CNN behavior more explainable and more controllable. The results obtained demonstrated the feasibility of real‐time markerless lung tumor segmentation in kV XF images for IGRT.
Keywords: attention‐based data augmentation, IGRT, kV X‐ray fluoroscopy, patient‐specific deep learning, tumor tracking and segmentation
1. INTRODUCTION
In radiotherapy, it is important to deliver a high dose to a tumor while reducing a dose to normal organs. In particular, the monitoring and synchronizing of respiratory movements is necessary for high‐precision radiotherapy of the thoracoabdominal organs such as lung and liver. Motion monitoring methods can be classified into two categories 1 , 2 : external monitoring by devices placed on patient surface 3 or directly sensing the surface 4 and internal monitoring by kilovoltage (kV) X‐ray fluoroscopy (XF) 5 or magnetic resonance imaging (MRI). 6 The insertion of fiducial markers around a tumor and tracking them on kV XF images was a breakthrough technique to ensure the tracking accuracy 5 ; however, the marker insertion is invasive to patients. Although MRI is a less invasive method, such MRI‐combined radiotherapy systems are not extensively available. 7 Therefore, the realization of markerless tumor tracking using kV XF images for image‐guided radiotherapy (IGRT) remains an important research topic in medical physics.
Many studies addressed the difficulties of markerless tumor tracking in XF images. 2 , 8 , 9 From the image processing viewpoint, we can distinguish the difficulties into four important factors:
Obstacle overlapping: For example, high‐contrast bone features projected on XF cause false tracking. These obstacles require to be suppressed 10 , 11 , 12 , 13 or recognized as unimportant (ignored). 14
Poor visibility: Because tumor contrast in XF is usually insufficient, the tumor position should be estimated by surrounding structures that may be more visible or the motion should be enhanced using XF subtraction. 15 , 16 , 17 , 18 , 19
Anatomy and/or respiration change: The underestimation of respiratory motion in four‐dimensional computer tomographic (4DCT) imaging, daily anatomical changes, and tumor shrinkage in response to irradiation cause the difference between planning and treatment sessions. 20 , 21 , 22 , 23 , 24 , 25 The respiratory motion pattern continuously varies in sessions. 26 , 27
Image quality difference: Digitally reconstructed radiography (DRR) and XF have different image quality, thus making their comparison difficult. 28 , 29 , 30
An advanced real‐time image processing method addressing the abovementioned problems is strongly required to prevent false tracking in XF images.
Artificial intelligence (AI), especially deep learning (DL), has recently developed as an advanced image processing tool. 31 , 32 While many AI studies deal with big data, we reported a conceptual study of patient‐specific DL, which uses patient‐specific convolutional neural networks (CNNs) trained by individual datasets. 14 Since our study, several similar studies have been reported. 33 , 34 , 35 The difference between our strategy and others’ strategies was whether the CNNs were trained by attention‐based or scenario‐based augmented datasets. Here, scenario‐based means simulating inter‐ and intrafraction variations of CT images (deformation, translation, and rotation) and thereafter creating anatomically correct DRRs. 34 In contrast, our attention‐based augmentation intentionally generated anatomically partial‐incorrect DRRs where soft tissues were placed at the right positions but bony structures were randomly overlayed (RO) at the wrong positions. 14 , 36 This strategy is based on a reasonable hypothesis that since DL is a data‐driven statistical optimization method, its behavior depends on the co‐occurrence probability (CoOCP) of features and labels in the training dataset. CNNs will recognize the image features with high CoOCP as important and ignore ones with low CoOCP as unimportant. That is, our strategy aims to control the CNN's attention by the artificial difference of CoOCP in order to focus on soft tissues while ignoring bones. 14 However, our conceptual study used DRRs in both training and testing; verification using clinical XF images was not performed because the determination of comparable ground truths (GTs) of target position and shape in clinical XF images was complex. To date, the accuracy of tumor segmentation in clinical XF using DLs learned with DRRs generated only from planning CT data has not been reported. Furthermore, the DL behavior in IGRT was not examined by explainable techniques.
The first aim of this study is to visualize CNN attention to the evidence that the proposed method provides explainable and controllable DL behavior. The second purpose is to report a real‐time lung tumor segmentation accuracy in clinical kV XF images using the proposed DL method.
2. MATERIALS AND METHODS
2.1. Patient selection and ethics statement
A retrospective analysis was performed on 10 lung cancer patients undergoing proton therapy with approval (number: H28‐170) from the Ethics Committee of our hospital. The criterion for patient selection was whether the stored sequential XF images were appropriate for this study: longer than one respiratory cycle and without information loss because of halation (details in Section 2.5). Table 1 summarizes the tumor characteristics.
TABLE 1.
Tumor characteristics
|
4D pCTV (T00‐T50) Centroid shift (mm) |
4D pCTV Jaccard index |
4D pCTV Hausdorff distance (mm) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Patient | Stage | Site | Posture | Prescribed dose (GyE)/fractions |
4D T50% CTV (cc) |
Frontal (LR/SI) |
Lateral (AP/SI) |
Frontal | Lateral | Frontal | Lateral |
| 1 | IA2 | RUL | Prone | 72.6/22 | 10.5 | 0.9/6.5 | 3.5/6.4 | 0.84 | 0.86 | 1.7 | 1.6 |
| 2 | IA2 | RLL | Prone | 72.6/22 | 18.9 | 0.2/1.7 | 1.0/1.8 | 0.91 | 0.91 | 1.5 | 1.8 |
| 3 | IVa | RLL | Supine | 66/10 | 11.2 | 0.4/25.6 | 2.8/25.2 | 0.91 | 0.92 | 1.6 | 1.5 |
| 4 | IA2 | RUL | Supine | 66/10 | 10.3 | 0.1/0.1 | 0.6/0.1 | 0.99 | 0.96 | 0.3 | 0.3 |
| 5 | IA | RUL | Supine | 66/10 | 14.9 | 1.6/1.5 | 2.6/1.2 | 0.87 | 0.87 | 1.4 | 2.4 |
| 6 | IA2 | LUL | Supine | 66/10 | 6.7 | 3.2/1.2 | 0.9/1.2 | 0.85 | 0.86 | 1.2 | 1.2 |
| 7 | IIA | RML | Supine | 80/20 | 41.3 | 0.1/0.4 | 0.4/0.1 | 0.98 | 0.97 | 1.0 | 1.0 |
| 8 | IA | RUL | Prone | 72.6/22 | 25.5 | 0.7/6.5 | 0.6/6.3 | 0.91 | 0.86 | 5.3 | 6.6 |
| 9 | IIB b | RLL | Supine | 66/10 | 69.4 | 1.5/11.5 | 3.0/10.4 | 0.67 | 0.72 | 12.3 | 10.4 |
| 10 | IA2 | RLL | Supine | 66/10 | 28.6 | 1.1/6.1 | 0.5/ 8.7 | 0.75 | 0.63 | 10.9 | 10.9 |
Note: (a) Lung metastasis of rectum cancer. (b) This CTV included two adjacent GTVs. Jaccard index and Hausdorff distance were evaluated after centroid matching.
Abbreviations: LUL, left upper lobe; pCTV, projected‐clinical‐target‐volume; RLL, right lower lobe; RML, right middle lobe; RUL, right upper lobe; GyE, Gray‐equivalent dose.
2.2. Workflow from CT imaging to target definition
As per our radiotherapy procedure, respiratory‐gated 3D CT images in the exhalation phase and 10‐phased 4DCT images were acquired under free‐breathing by a CT (Optima 580 W; GE Healthcare, WI, USA) with a respiratory monitoring system (AZ‐733VI; Anzai Medical Co. Ltd, Tokyo, Japan). The spatial resolution of CT images was 1.07 mm in left‐right (LR) and anterior‐posterior (AP) directions; furthermore, the slice pitch corresponding superior‐inferior (SI) direction was 2.5 mm. Then, a radiation oncologist delineated the gross‐tumor‐volume and clinical‐target‐volume (CTV) on the gated 3DCT images using a planning support system (MIM Maestro: MIM Software Inc., OH, USA). The CTVs were automatically propagated on the 10‐phased 4DCTs by MIM nonlinear deformable image registration function. 37 , 38 Only for patient 3, a medical physicist manually set 30‐mm diameter spheres on 4DCT images to identify the target position because the automatic contour propagation did not work well because of significant motion artifacts in the 4DCT images.
2.3. Workflow in training data generation
2.3.1. DRR and label calculation
The training dataset in this study was special for each patient and frontal/lateral XF angle (patient‐and‐angle). First, all CT values were converted to the linear attenuation coefficient (LAC: μ) using the interpolation of the energy‐LAC tables for multiple tissue substitutes, 39 considering tube voltage and effective energy (E eff) in the CT and XF (Table 2). The LAC contributions of the scatterer (μscat) were provided in the table. 39 The LACs were distinguished into the contribution of soft tissue () and that of bone (μbone) by the LAC threshold (μ200) corresponding to the Hounsfield unit (HU) of 200.
TABLE 2.
Summary of the linear attenuation coefficient (LAC: μ) for multiple tissue substitutes39
| Lung | Water | Griffith‐Bone |
Threshold in this study |
||||||
|---|---|---|---|---|---|---|---|---|---|
| Modality |
Tube voltage (kV) |
E eff (keV) |
μ (cm‐1) |
μ scat (cm‐1) |
μ (cm‐1) |
μ scat (cm‐1) |
μ (cm‐1) |
μ scat (cm‐1) |
μ 200 (cm‐1) |
| XF | 50 | 28 | 0.114 | 0.065 | 0.399 | 0.235 | 1.150 | 0.304 | 0.642 |
| XF | 70 | 31 | 0.098 | 0.063 | 0.345 | 0.227 | 0.915 | 0.293 | 0.529 |
| XF | 90 | 34 | 0.088 | 0.062 | 0.309 | 0.222 | 0.753 | 0.283 | 0.453 |
| CT | 120 | 56 | 0.059 | 0.052 | 0.212 | 0.196 | 0.343 | 0.244 | 0.254 |
| Calculated CT value (HU) | −722 | 0 | 618 | 200 | |||||
Note: Lung, Water and Griffith‐Bone are tissue substitutes.39
Abbreviations: CT, computer tomography; E eff, effective energy; HU, Hounsfield unit; μ scat, scatter contribution of LAC; μ 200, LAC threshold to separate contribution of soft tissue from that of bone; XF, X‐ray fluoroscopy.
The LAC at an arbitrary point was represented as follows:
| (1) |
The 2D matrixes for the calculation of soft tissue (M soft), bone (M bone), and scatterer (M scat) were defined as follows:
| (2) |
| (3) |
| (4) |
where s was the ray tracing path from the X‐ray source to an arbitrary point (x, y) on a detector plane, was the calculation step length. The M scat was a semiempirical approximation of the multiple scattering effects using a 2D Gaussian distribution. The g had a sigma of 6 mm that could blur local image features. The 2D convolution operator was denoted as ⊗.
The DRR (I DRR) as a 2D image could be concisely presented using the following equation,
| (5) |
where operator ○ means the Hadamard product, w was the variable weight. The nonlinear contrast differences between DRR and XF were compensated by patient‐and‐angle‐specific lookup tables (f LUT). The f LUT was determined by pairing the sorted pixel values of the DRR and the XF image obtained on the same day but not the test XF images.
The label images contained projected‐CTV shapes (pCTV), which were calculated based on whether each ray tracing passed through the CTV.
| (6) |
2.3.2. Data augmentation
Baseline
First, the 4DCT data were augmented using 3D rotation (± 1° in coronal/sagittal and ± 2° in axial with 1° interval). Next, both DRRs and labels were generated using the abovementioned method with slight modifications to make contrast variations,
| (7) |
Here, the superscript R indicates that the images were randomly affine transformed within positions (±50 pixels; ±26 mm) and angles (±2°), and w was from 0 to 0.1. Finally, both DRRs and labels were augmented using 2D crop (shift within ±25 pixels; 13 mm), 2D resize (within ±5%), and angle (±2°).
We defined these datasets containing anatomical‐correct DRRs and labels as baselines. The DRRs and labels had 256 × 256 pixels, which corresponded to about 0.52‐mm resolution at the isocenter.
Random overlay
As reported in our conceptual study, 14 the RO of bones aimed the low positional CoOCP between bones and labels, and high positional CoOCP between soft tissues and labels. The following equation shows the modified RO operation in which bone DRRs and scatter components were RO on the soft‐tissue DRRs,
| (8) |
Here, the random affine transformation was within positions (±50 pixels; ±26 mm) and angles (±2°).
Noise injection
Our CT data with coarse 2.5‐mm slice pitch made the DRR quality different from the XF quality primarily in local image features rather than global ones. To avoid overfitting the local feature in DRRs, directing the CNN attention to global ones would be effective. The difference in CoOCP in the image appearance by noise injection (NI) may control the CNN attention because NI easily destroyed local and fine image features while preserving the global ones. The following expression shows the augmented DRR by NI,
| (9) |
where I rand is a uniform noise image with random fractional values between ± 1 at each pixel. The noise intensity coefficient α varied up to 15% in the 8‐bit image scale.
2.4. Workflow in training CNN models
The CNN model was U‐Net 40 because it was more standard for segmentation than SegNet 41 in our previous study. 14 Loss function was defined using the Jaccard index (JI), 42 a similarity coefficient calculating intersection over union,
| (10) |
| (11) |
where union T and L indicates areas in training pCTV and label pCTV (Figure 1). Each block in Figure 1 has three set of the convolution (3 × 3), the ReLU activation, and the batch normalization layer. The number of filters of all convolutions was constant (32). The optimizer was Adam (learning rate of 1.0 × 10−2). CNNs were trained up to 10 epochs with increase in batch size from 4 to 40. 43 In the DL training stage, each patient‐and‐angle‐specific CNN was optimized.
FIGURE 1.
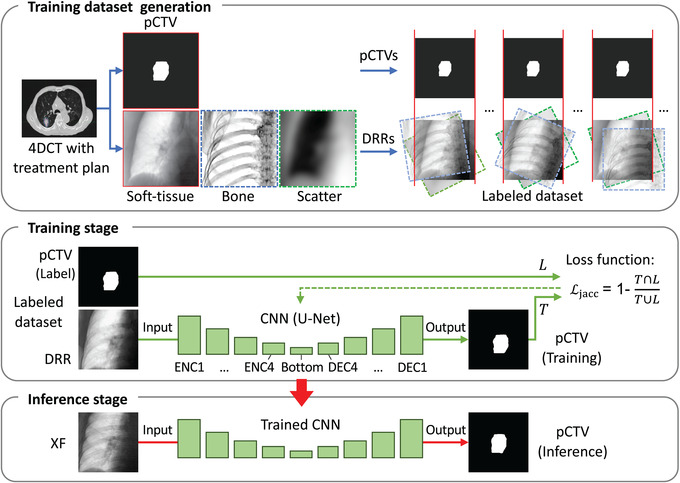
Workflow of the proposed method. 4DCT, four‐dimensional computer tomography; CNN, convolutional neural networks; DEC, decoder block; DRR, digitally reconstructed radiograph; ENC, encoder block; pCTV, projected‐clinical‐target‐volume; XF, X‐ray fluoroscopic image
2.5. Workflow in acquisition and selection of test XF image
The XF images were acquired during patient positioning before treatment sessions using a pair of orthogonal XF systems with X‐ray tubes and image intensifiers (I.I.) (DAR‐3000; Shimadzu Co., Kyoto, Japan) equipped on our proton therapy system (PROBEAT; Hitachi Ltd., Tokyo, Japan). In this study, the typical tube voltage for frontal and lateral XFs was 60−80 and 70−90 kV, respectively. The tube output was 0.08 mAs/frame. The 30 fps XF imaging doses of 60−90 kV tube voltages were measured using a glass dosimeter (GD‐352M; Chiyoda Technol Co., Tokyo, Japan). The dose rates at the isocenter were 0.12–0.35 mGy/s in air and 0.02–0.09 mGy/s at 100 mm depth in a water‐equivalent phantom. We developed a system that can store the XFs as 8‐bit gray‐scale images at a rate of up to 30 fps via a frame grabber board (Solios aA/XA; Matrox Imaging System Ltd., Quebec, Canada) and can record the respiratory signal detected by the laser sensor in the monitoring system. 4 Note that many stored XF images included halation in lung region because of the small dynamic range of I.I., as well as required manual adjustment of the XF contrast by radiologists to verify the relationship of bone structures for positioning. In addition, we sometimes used Pb shields to reduce X‐ray overexposure through a polyurethane patient‐immobilization device or air. By selecting the sequential test images taken without halation and the exposition longer than one respiration cycle, the XFs acquisition dates ranged from 4 to 26 days after CT imaging. Original test XF images had the size of 1024 × 1024 pixels; the center 512 × 512 pixels were resampled into 256 × 256 pixels, which correspond to ∼0.52 mm resolution at the isocenter.
2.6. Experiments
2.6.1. Calculation environment
The DL calculations were run on a computer with CPU Core i7‐9800X (Intel Co., CA, USA), GPU Quadro RTX 8000 (NVIDIA Co., CA, USA), OS Windows 10 Pro (Microsoft Co., WA, USA), Framework TensorFlow 2.1.0. (Google Inc., CA, USA), and Python 3.7.7 (opensource).
2.6.2. Comparison of data augmentation effects
We investigated how the same U‐Net models trained using different datasets affect the segmentation result. The lateral angle of patient 9 was selected as the most complex case where XF images had a large tumor deformity, almost overlapping with the spine and partially overlapping with the diaphragm. Figure 2 shows augmented DRRs by baseline, NI, and RO, and an XF. We trained U‐Net(A) with baseline data, U‐Net(B) with NI‐augmented data from baseline, U‐Net(C) with RO‐augmented data from baseline, and U‐Net(D) with NI‐and‐RO augmented data from baseline. All training was performed with the same number of 2000 image pairs (10 phases of 4DCT × 200 images). After training, the four trained U‐Nets transformed a test XF image of the expiratory phase (T50) into inferred pCTV images. We visualized the region of CNN attention as heatmaps using Grad‐CAM 44 to investigate the behavior of DLs.
FIGURE 2.
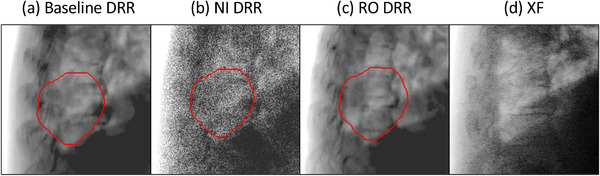
Examples of the digitally reconstructed radiographs (DRRs) augmented by the proposed methods, and a clinical X‐ray fluoroscopic (XF) image. The red contours indicate projected‐clinical‐volume. NI, noise injection; RO, random overlay
2.6.3. Test for all patients
Basically, the patient‐and‐angle‐specific datasets were augmented up to 2000 image pairs using the proposed RO and NI. Figure 3 shows four examples of training DRRs. Because of insufficient slice coverage of 4DCT imaging in patients 1−4 and 7, additional 500 image pairs were augmented from gated 3DCTs. A total of 2500 training image pairs were used to these patients. Because test images for patients 3 and 10 contained the Pb shield, the image portion of the shield was copied to the training DRRs using RO to avoid affecting tumor tracking (Figure 3). Twenty patient‐and‐angle‐specific CNNs were obtained after training. In the inference stage, the trained CNNs transformed the test XF images in the inferred pCTV images. A total of 2430 XF images were examined in this study.
FIGURE 3.
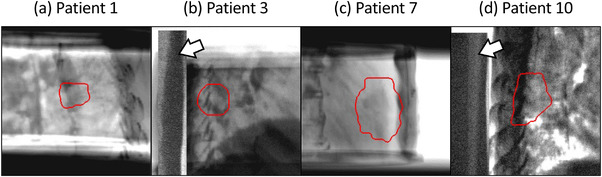
Examples of digitally reconstructed radiographs (DRRs) for training. The white arrows in (b) and (d) show the Pb shield reducing X‐ray overexposure. The red contours indicate the projected‐clinical‐volume.
2.7. GTs and evaluation indexes
2.7.1. GTs
We developed a 2D−3D matching method with multitemplates and score classification to identify GTs as segmented areas in the test XF images (Appendix A). For each test image, we calculated the GT and standard deviation (GT_SD) by considering the top 5% template‐matching score. The mean GT_SD in each direction over ten patients was about 0.7 mm (1σ). A certified oncologist and two medical physicists verified the GT results in the test 2430 XF images and later concluded that the results were acceptable. In terms of methodology, this GT determination process using machine learning (multi‐template and classification) and the manual was similar to another study. 35
2.7.2. Evaluation indices
The inferred pCTVs were compared with GTs using mean absolute error (MAE) and the 95th percentile of absolute error (95AE) as centroid difference, JI as the segmentation accuracy, and Hausdorff distance (HD) 45 as the maximum difference between segmented edges. The estimated 3D tracking errors () were synthesized using the root sum squares of statistical errors in each direction.
| (12) |
The e LR, , e AP, and demonstrated the statistical errors in LR and SI directional in frontal XFs and in AP and SI directions in lateral XFs, respectively.
3. RESULTS
3.1. Processing time
The CNN training time was 24 or 30 min for patient‐and‐angle‐specific dataset containing 2000 or 2500 paired images. Typically, the loss value decreased to 0.05 after 10 epoch training. The inference processing time for each test XF was 8 ms/frame.
3.2. Comparison of data augmentation effects
Figure 4 shows the impact of data augmentations on attention heatmaps and segmentation results. The heatmaps calculated using Grad‐CAM 44 highlight the attention regions at three blocks of U‐Nets. The U‐Net(A) focused its attention on the bone features (intervertebral disk and spinous process) and then falsely tracked the pCTV. In the U‐Net(B) heatmap, the extensively distributed regions of interest indicate that NI directed the CNN's attention to global image features. The U‐Net(C) heatmap demonstrated that the bone RO directed the attention on the diaphragm and soft tissue rather than the bone. U‐Net(D) with NI and RO augmentation focused its attention close to the diaphragm and target boundary, thus resulting in the best segment performance.
FIGURE 4.
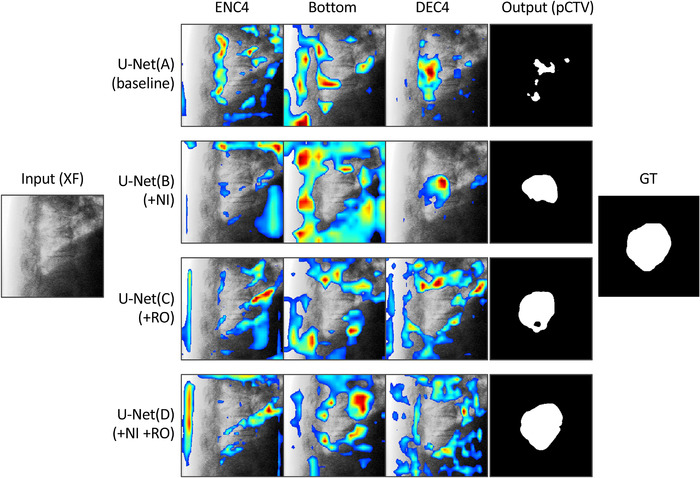
Impact of data augmentations on attention heatmaps and segmentation results. The heatmaps calculated using Grad‐CAM highlight the attention regions. The four convolutional neural networks (CNNs) had the same U‐Net structure; however, trained by different datasets (A: baseline, B: baseline + noise injection [NI], C: baseline + random overlay [RO], D: baseline + NI + RO). DEC4, decoder block next to the bottom block; ENC4, encoder block next to the bottom block; GT, ground truth; pCTV, projected clinical‐target‐volume; XF, X‐ray fluoroscopic image
3.3. Inference results for all patients
Figure 5 shows the segmentation results at the exhalation phase (T50) for normal tumor‐deformation cases (patients 1−8), and those at inhalation (T00), exhalation (T50), and middle phases for large tumor‐deformation cases (patients 9 and 10) are shown in Figure 6. Figure 7 shows the pCTV centroid trajectory in the best case of lateral XFs (patient 1), the worst case (patient 9), the largest deformation case in JI (patient 10), and the largest motion case (patient 3). Table 3 lists the calculated tracking errors for all patients. Both JI and HD are listed in Table 4. Figure 8 shows the dependence of 95AE on days between CT imaging and test XF imaging.
FIGURE 5.
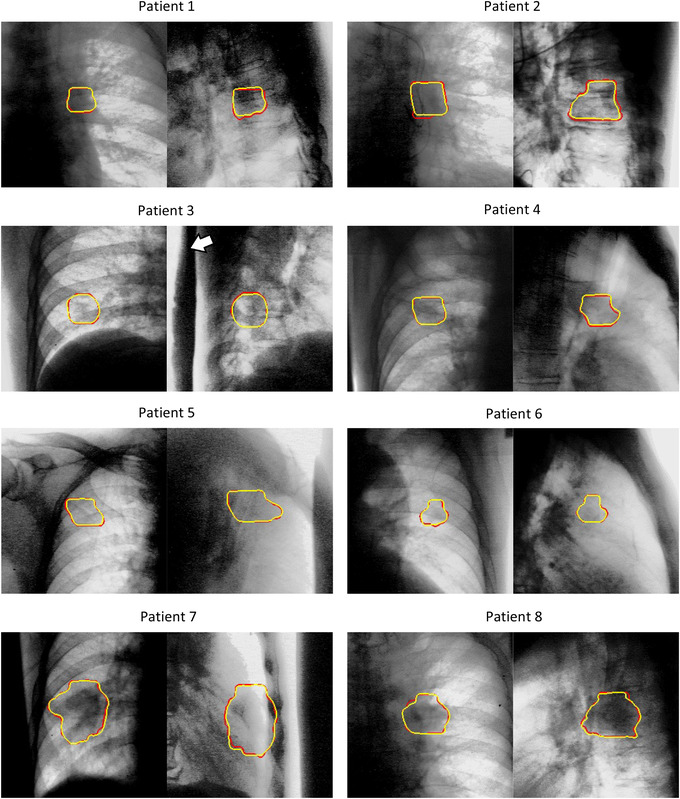
Segmentation results in the exhalation phase T50. The pair images show frontal and lateral X‐ray fluoroscopic images (yellow contour: projected‐clinical‐target‐volume by the proposed method, red contour: ground truth). The white arrow shows a Pb shield that reduces overexposure. The image contrast was tuned to enhance the view.
FIGURE 6.
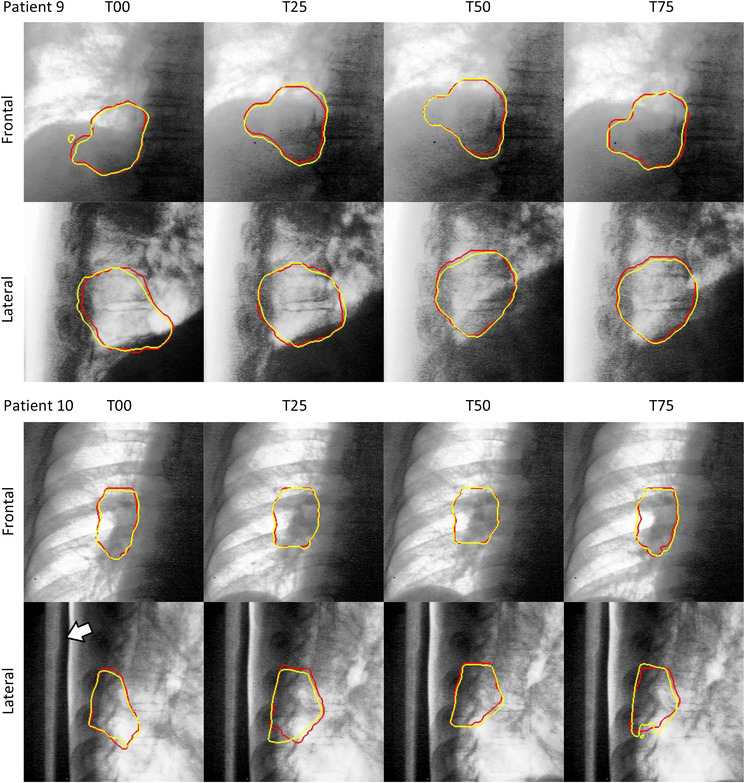
Segmentation results for highly deformed targets (yellow contour: projected‐clinical‐target‐volume by the proposed method, red contour: ground truth, T00: Inhalation phase, T50: exhalation phase, T25 and T75: middle phases of inhalation and exhalation, respectively). The white arrow shows a Pb shield that reduces overexposure. The image contrast was then tuned to enhance the view.
FIGURE 7.
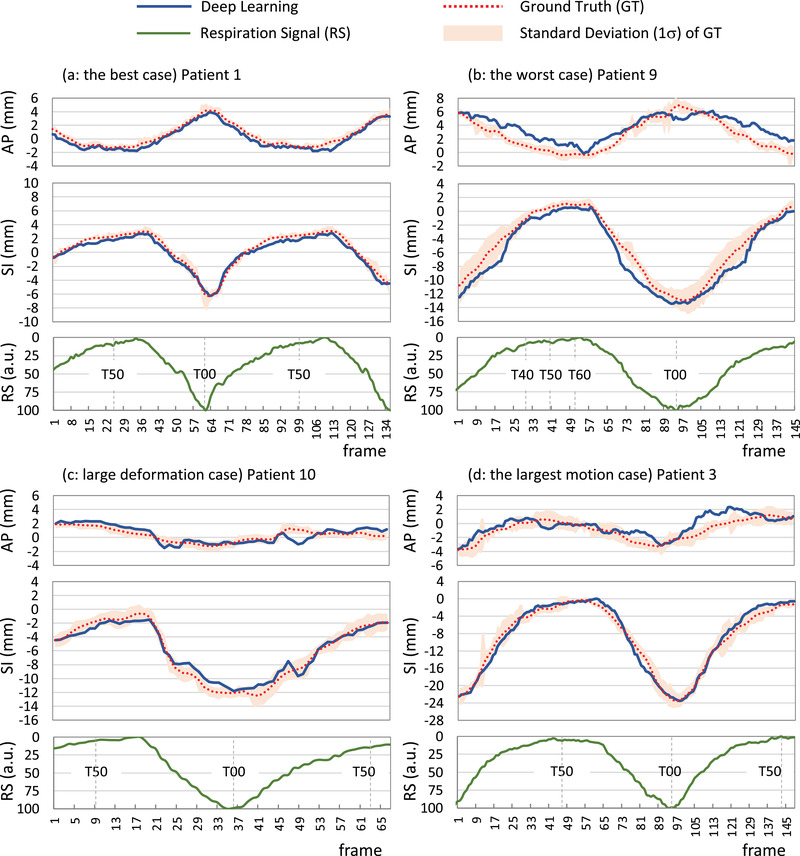
Centroid motion of the projected‐clinical‐target‐volume in lateral X‐ray fluoroscopy using deep learning and ground truth and respiration signals
TABLE 3.
Tracking errors in all respiration phases
| Frontal | Lateral | Estimated 3D error | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LR (mm) | SI (mm) | AP (mm) | SI (mm) | Mean days | MAE (mm) | 95AE (mm) | |||||||
| Patient | Days | MAE | 95AE | MAE | 95AE | Days | MAE | 95AE | MAE | 95AE | |||
| 1 | 12 | 0.52 | 0.96 | 0.58 | 1.15 | 8 | 0.41 | 0.79 | 0.46 | 0.82 | 10 | 0.85 | 1.60 |
| 2 | 19 | 0.75 | 1.08 | 0.70 | 1.21 | 15 | 0.63 | 1.04 | 0.83 | 1.86 | 17 | 1.24 | 2.17 |
| 3 | 20 | 0.72 | 1.52 | 1.00 | 2.50 | 25 | 0.83 | 2.30 | 0.92 | 2.13 | 23 | 1.46 | 3.60 |
| 4 | 9 | 0.18 | 0.34 | 0.44 | 0.72 | 9 | 0.45 | 0.81 | 0.86 | 1.19 | 9 | 0.84 | 1.32 |
| 5 | 26 | 0.21 | 0.54 | 0.56 | 1.21 | 20 | 0.63 | 1.06 | 0.45 | 1.08 | 23 | 0.84 | 1.65 |
| 6 | 22 | 0.57 | 1.55 | 0.60 | 1.19 | 22 | 0.43 | 1.13 | 0.67 | 1.45 | 22 | 0.96 | 2.33 |
| 7 | 14 | 0.26 | 0.55 | 0.31 | 0.70 | 4 | 0.18 | 0.36 | 0.64 | 1.36 | 9 | 0.59 | 1.27 |
| 8 | 14 | 0.77 | 1.51 | 0.51 | 1.37 | 20 | 0.36 | 0.88 | 0.40 | 0.92 | 17 | 0.97 | 2.10 |
| 9 | 23 | 0.95 | 1.96 | 0.72 | 1.73 | 23 | 1.31 | 2.52 | 1.16 | 2.70 | 23 | 1.88 | 3.92 |
| 10 | 22 | 0.43 | 1.30 | 0.80 | 1.85 | 14 | 0.56 | 1.51 | 0.65 | 1.47 | 18 | 1.02 | 2.60 |
| Average | 18 | 0.54 | 1.13 | 0.62 | 1.36 | 16 | 0.58 | 1.24 | 0.71 | 1.50 | 17 | 1.07 | 2.26 |
Abbreviations: AP, anterior‐posterior; LR, left‐right; MAE, mean absolute error; SI, superior‐inferior; 95AE, the 95percentile absolute error.
TABLE 4.
Jaccard index and Hausdorff distance
| Jaccard index | Hausdorff distance (mm) | |||
|---|---|---|---|---|
| Patient | Frontal Mean ± SD | Lateral Mean ± SD | Frontal Mean ± SD | Lateral Mean ± SD |
| 1 | 0.84 ± 0.04 | 0.90 ± 0.02 | 2.2 ± 0.6 | 1.2 ± 0.4 |
| 2 | 0.86 ± 0.02 | 0.85 ± 0.03 | 2.4 ± 0.5 | 2.9 ± 0.6 |
| 3 | 0.88 ± 0.04 | 0.86 ± 0.06 | 1.6 ± 0.7 | 1.7 ± 0.8 |
| 4 | 0.94 ± 0.01 | 0.90 ± 0.03 | 0.6 ± 0.4 | 1.1 ± 0.3 |
| 5 | 0.91 ± 0.03 | 0.90 ± 0.04 | 1.3 ± 0.6 | 1.6 ± 0.8 |
| 6 | 0.88 ± 0.05 | 0.90 ± 0.06 | 1.1 ± 0.6 | 0.9 ± 0.7 |
| 7 | 0.94 ± 0.01 | 0.91 ± 0.01 | 1.8 ± 0.3 | 2.8 ± 2.0 |
| 8 | 0.88 ± 0.04 | 0.88 ± 0.02 | 2.9 ± 0.5 | 2.8 ± 1.2 |
| 9 | 0.87 ± 0.05 | 0.90 ± 0.03 | 4.9 ± 2.5 | 3.7 ± 1.8 |
| 10 | 0.91 ± 0.03 | 0.88 ± 0.05 | 2.4 ± 1.7 | 3.1 ± 2.0 |
| Average | 0.89 ± 0.03 | 0.89 ± 0.04 | 2.1 ± 0.8 | 2.2 ± 1.1 |
Abbreviation: SD, standard deviation.
FIGURE 8.
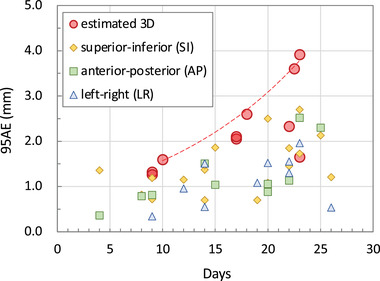
Dependence of the 95th percentile of absolute error (95AE) on the interval days between computer tomographic imaging and test X‐ray fluoroscopic imaging. The dashed envelope approximates the bounding points of the estimated 3D 95AE.
4. DISCUSSIONS
4.1. Novelty of this study
This study was the first attempt to visualize the CNN attention heatmap and explain the DL behavior in IGRT. The application of DL to radiotherapy requires high reliability, and its behavior should not be a black box. Therefore, it is meaningful that our method utilizing the difference of CoOCP enabled to focus CNN on the desired image features while ignoring the unimportant ones, thus improving the explanation and control of DL.
To our knowledge, this was the first feasibility study of real‐time markerless lung tumor segmentation using patient‐specific DL using only training DRRs generated from planning CT data. Although this analysis had only 10 cases, the tracking accuracy within 4 mm sustaining up to 23 days demonstrated the robustness of the method and its clinical feasibility.
4.2. Attention‐based augmentation as explainable and controllable AI
Several medical AIs presume that the appropriate dataset should be anatomically accurate and have high‐quality images. 46 , 47 However, the trained U‐Net(A) having such anatomical‐correct dataset wrongly focused its attention on prominent bony structures and resulted in false tracking (Figure 4). Probably, this was attributed to the unintentional high CoOCP of bones with labels because of the extremely small lung motion in expiratory phases (T40, T50, T60) as in Figure 7b. In contrast, our attention‐based dataset included the anatomically partial‐incorrect DRRs by RO. The artificial difference in CoOCP leads to efficient feature extraction because the intentional mixing of such images with low CoOCP relatively increases the CoOCP of other truly important features to be extracted. Indeed, as predicted, the U‐Net(D) trained by our attention‐based augmentation successfully focused on soft tissue and global image feature and resulted in a good segmentation. This strategy of shifting CNN's attention from prominent features to truly important ones by artificial CoOCP will be helpful in other medical AI studies.
4.3. Methodological properness of the proposed method as tumor tracking
We can discuss the reliability of the proposed method in terms of the four difficulties mentioned in the introduction.
Obstacle overlapping: The RO could control the focus of CNN attention. Similarly, we could reduce the influence of additional obstacles such as the Pb shield in XF images. Without knowing the exact location of obstacles in advance, we could include them in the training images by RO and track the tumor without being affected by them.
Poor visibility: The CNN nature is consistent with the previous results that more visible surroundings can improve tracking accuracy. 19 In CNN, the more layers are stacked, the wider is the receptive field, for example, the receptive field at the bottom layer of our CNNs corresponds to the surrounding 186‐pixel square (53% of the image area). From this CNN feature itself, one may expect that certain latent features correlating with the tumor motion in the receptive field will be extracted without manual processing.
Anatomy and/or respiration change: The RO, enabling more soft tissue flexibility than anatomical‐correct DRRs, makes our method robust to underestimating tumor motion in planning 4DCT and irregular motion patterns in treatment sessions. This is supported by the fact that the tracking error did not increase in the lateral XFs of patient 2, although approximately 10‐mm change was observed in respiratory motion ranges between planning 4DCT (2.0 mm) and clinical XFs (11.6 mm).
Image quality difference: The DRR contrast was approximately compensated by the LUT. Although the spatial resolution was not improved, we addressed it by the NI focusing the CNN attention on the global image features rather than local ones. In this study, we set the noise level up to 15% as a tentative optimal value after several trials. Further improvement in DRR quality 48 , 49 may reduce noise and focus more CNN attention on local features. However, even in this case, it will be necessary to prevent overlearning with local features, and not for image quality differences but also for daily anatomical changes that we cannot measure in advance.
4.4. Comparison with other studies
There are no similar studies for comparison of segmentation in clinical kV XF images; however, regarding the tracking position, we can compare the DL studies reported by Wei et al. 34 and Hirai et al. 35 Their lung tracking errors in MAE were 1.8 mm (SI)/1.0 mm (LR) for 15 cases 34 and 0.76 mm (SI)/1.00 mm (LR)/1.12 mm (AP) for five cases. 35 In contrast, our MAE for 10 cases was 0.67 mm (SI)/0.54 mm (LR)/0.58 mm (AP). Moreover, our CNN training time (30 min) and inference time (8 ms) were over 22 and about five times faster, respectively, compared to their reports (Wei: 20 h and 40 ms, Hirai: 11 h and 38 ms). Compared with other non‐DL methods using lung kV XFs, our SI error (0.67 mm) and 3D 95AE (1.3−3.9 mm) were comparable with that of Teske et al. (0.9 mm) 11 and Shieh et al.’s (2.6−5.8 mm). 50 Moreover, good correlations between SI trajectories and respiratory signals were similar to those in the recent reports. 51 , 52 Note that the tracking accuracy is highly case‐dependent, thus making the direct comparison difficult.
4.5. Limitations
Because the 10‐phased 4DCT data with 2.5 mm slice in this study were coarse in time and space, the tracking accuracy tended to deteriorate in large deformation cases. Therefore, the GT accuracy in our analysis was not perfect. While our calculation accounted for random displacements beyond the motion range, it only accounted for the same deformation as the discrete 10‐phased 4DCT, that is, we could not reflect larger deformations in the GT. Nevertheless, our GT calculation method will be helpful in similar studies. More sophisticated verifications that include nonlinear deformation would be possible if advanced methods will provide an instantaneous 3D reconstruction with sufficient accuracy from a kV XF image. 53
Because of the mechanical limitations of our system, the test XF images were taken in the frontal and lateral directions only; the tracking accuracy in arbitrary angles was unclear. As the test XF images were not taken during treatment beam irradiation, we must verify the influence of XF image degradation by scattered radiation from treatment beams. 54
This study was primarily performed with right lung patients with relatively large tumors; more complicated cases, such as left lung tumors affected by the heartbeat, should be examined later. While the proposed method that leverages the data‐driven nature of DL is promising, additional study is required to validate it in a broader group of patients.
5. CONCLUSIONS
This study visualizes the CNN attention in a markerless lung tumor segmentation method using patient‐specific DL. We confirmed that the proposed attention‐based data augmentation with RO and NI yielded explainable and controllable CNN behavior. The tracking accuracy demonstrated the feasibility of the proposed method as a real‐time segmentation method for markerless lung tumors in kV XF images for IGRT.
CONFLICT OF INTEREST
The AMED grant (JP19he2302001) involves Hitachi Ltd. The authors TT, TS, and HS received a software fee related to this work from Hitachi Ltd. after the submission of this report. The author HS has a research grant by Hitachi Ltd. unrelated to this work. The other authors have no conflict of interest to disclose.
ACKNOWLEDGMENTS
This research was supported by Japan Society for the Promotion of Science under grant number: 17K09054 and AMED under grant number: JP19he2302001. The authors would like to thank Dr. Yutaro Mori and Mr. Koichi Tomoda for their valuable comments. We appreciate all the staff of Proton Medical Research Center, University of Tsukuba Hospital.
APPENDIX A. GROUND TRUTHS CALCULATION
A.1.
The GT segmentation in XF image was determined by modifying the 2D−3D matching method in Tashiro et al.’s study. 55 They divided a CT data into two volumes of interest (VOIs); however, the overlap state was discretely calculated by replacing the larger CT value of two VOIs. In contrast, we divided the LAC value using Equation 1 and continuously calculated the mixed state by adding two VOIs (Figure A1). In step 1, the 3D LAC volume in an arbitrary phase of 4DCT was divided into μsoft and μbone. In step 2, two 3D LAC were shifted and rotated using a random affine transformation. Next, the 3D LACs were projected as DRRs, and the corresponding pCTVs were projected too. For template matching (TPM) using the normalized cross‐correlation, we generated ∼1000 DRR templates by cropping arbitrary rectangles region of interest (ROI). These size‐different multitemplates would be effective because setting smaller ROI makes the distortion effect relatively minor and can possibly be approximated using a linear transformation. In step 3, the TPM was processed in the test XF images. From the top 5% TPM scores, we calculated the score‐weighted mean position (SWMP) and standard deviation (GT_SD). The GT segmentations for each XF frame were determined by placing the pCTVs corresponding to the best DRR templates on the SWMPs. The GT positions of the tumor were calculated by the centroid of the GT segmentation. However, the multitemplate score‐classification method was so time‐consuming that the calculation time was >1 min for each XF frame.
FIGURE A1.
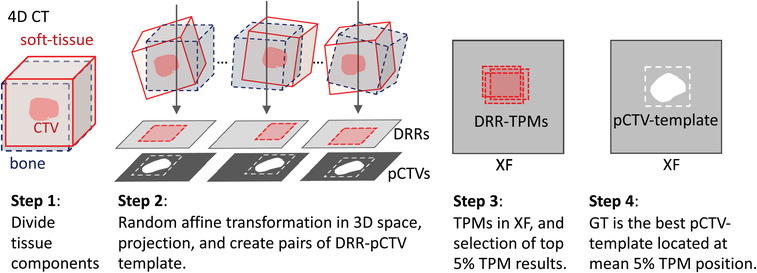
Workflow of ground truth (GT) detection. 3D, three‐dimension; 4D CT, four‐dimensional computer tomography; DRR, digitally reconstructed radiograph; pCTV, projected clinical‐target‐volume; XF, X‐ray fluoroscopy; TPM, template matching
Terunuma T, Sakae T, Hu Y, et al. Explainability and controllability of patient‐specific deep learning with attention‐based augmentation for markerless image‐guided radiotherapy. Med Phys. 2023;50:480–494. 10.1002/mp.16095
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are not available.
REFERENCES
- 1. Keall PJ, Mageras GS, Balter JM, et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76a. Med Phys. 2006;33(10):3874‐3900. doi: 10.1118/1.2349696 [DOI] [PubMed] [Google Scholar]
- 2. Bertholet J, Knopf A, Eiben B, et al. Real‐time intrafraction motion monitoring in external beam radiotherapy. Phys Med Biol. 2019;64(15):15TR01. doi: 10.1088/1361-6560/ab2ba8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ohara K, Okumura T, Akisada M, et al. Irradiation synchronized with respiration gate. Int J Radiat Oncol Biol Phys. 1989;17(4):853‐857. doi: 10.1016/0360-3016(89)90078-3 [DOI] [PubMed] [Google Scholar]
- 4. Tsunashima Y, Sakae T, Shioyama Y, et al. Correlation between the respiratory waveform measured using a respiratory sensor and 4D tumor motion in gated radiotherapy. Int J Radiat Oncol. 2004;60(1):951‐958. doi: 10.1016/j.ijrobp.2004.06.026 [DOI] [PubMed] [Google Scholar]
- 5. Shirato H, Shimizu S, Kunieda T, et al. Physical aspects of a real‐time tumor‐tracking system for gated radiotherapy. Int J Radiat Oncol. 2000;48(4):1187‐1195. doi: 10.1016/S0360-3016(00)00748-3 [DOI] [PubMed] [Google Scholar]
- 6. Raaymakers BW, Raaijmakers AJE, Kotte ANTJ, Jette D, Lagendijk JJW. Integrating a MRI scanner with a 6 MV radiotherapy accelerator: dose deposition in a transverse magnetic field. Phys Med Biol. 2004;49(17):4109‐4118. doi: 10.1088/0031-9155/49/17/019 [DOI] [PubMed] [Google Scholar]
- 7. Keall PJ, Nguyen DT, Brien RO, et al. Review of real‐time 3‐dimensional image guided radiation therapy on standard‐equipped cancer radiation therapy systems: are we at the tipping point for the era of real‐time radiation therapy? Radiat Oncol Biol. 2018;102(4):922‐931. doi: 10.1016/j.ijrobp.2018.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Czerska K, Emert F, Kopec R, et al. Clinical practice vs. state‐of‐the‐art research and future visions: report on the 4D treatment planning workshop for particle therapy–Edition 2018 and 2019. Phys Medica. 2021;82:54‐63. doi: 10.1016/j.ejmp.2020.12.013 [DOI] [PubMed] [Google Scholar]
- 9. Mylonas A, Booth J, Nguyen DT. A review of artificial intelligence applications for motion tracking in radiotherapy. J Med Imaging Radiat Oncol. 2021;65(5):596‐611. doi: 10.1111/1754-9485.13285 [DOI] [PubMed] [Google Scholar]
- 10. Xu T, Ducote JL, Wong JT, Molloi S. Dynamic dual‐energy chest radiography: a potential tool for lung tissue motion monitoring and kinetic study. Phys Med Biol. 2011;56(4):1191‐1205. doi: 10.1088/0031-9155/56/4/019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Teske H, Mercea P, Schwarz M, Nicolay NHNH, Sterzing F, Bendl R. Real‐time markerless lung tumor tracking in fluoroscopic video: handling overlapping of projected structures. Med Phys. 2015;42(5):2540‐2549. doi: 10.1118/1.4917480 [DOI] [PubMed] [Google Scholar]
- 12. Haytmyradov M, Mostafavi H, Cassetta R, et al. Adaptive weighted log subtraction based on neural networks for markerless tumor tracking using dual‐energy fluoroscopy. Med Phys. 2020;47(2):672‐680. doi: 10.1002/mp.13941 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Tanaka R, Sanada S, Sakuta K, Kawashima H. Improved accuracy of markerless motion tracking on bone suppression images: preliminary study for image‐guided radiation therapy (IGRT). Phys Med Biol. 2015;60(10):N209‐N218. doi: 10.1088/0031-9155/60/10/N209 [DOI] [PubMed] [Google Scholar]
- 14. Terunuma T, Tokui A, Sakae T. Novel real‐time tumor‐contouring method using deep learning to prevent mistracking in X‐ray fluoroscopy. Radiol Phys Technol. 2018;11(1):43‐53. doi: 10.1007/s12194-017-0435-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Berbeco RI, Mostafavi H, Sharp GC, Jiang SB. Towards fluoroscopic respiratory gating for lung tumours without radiopaque markers. Phys Med Biol. 2005;50(19):4481‐4490. doi: 10.1088/0031-9155/50/19/004 [DOI] [PubMed] [Google Scholar]
- 16. Cui Y, Dy JG, Sharp GC, Alexander B, Jiang SB. Multiple template‐based fluoroscopic tracking of lung tumor mass without implanted fiducial markers. Phys Med Biol. 2007;52(20):6229‐6242. doi: 10.1088/0031-9155/52/20/010 [DOI] [PubMed] [Google Scholar]
- 17. Ionascu D, Jiang SB, Nishioka S, Shirato H, Berbeco RI. Internal‐external correlation investigations of respiratory induced motion of lung tumors. Med Phys. 2007;34(10):3893. doi: 10.1118/1.2779941 [DOI] [PubMed] [Google Scholar]
- 18. Lin T, Cerviño LI, Tang X, Vasconcelos N, Jiang SB. Fluoroscopic tumor tracking for image‐guided lung cancer radiotherapy. Phys Med Biol. 2009;54(4):981‐992. doi: 10.1088/0031-9155/54/4/011 [DOI] [PubMed] [Google Scholar]
- 19. Cerviño LI, Jiang Y, Sandhu A, Jiang SB. Tumor motion prediction with the diaphragm as a surrogate: a feasibility study. Phys Med Biol. 2010;55(9):N221‐N229. doi: 10.1088/0031-9155/55/9/N01 [DOI] [PubMed] [Google Scholar]
- 20. Ge J, Santanam L, Noel C, Parikh PJ. Planning 4‐dimensional computed tomography (4DCT) cannot adequately represent daily intrafractional motion of abdominal tumors. Int J Radiat Oncol. 2013;85(4):999‐1005. doi: 10.1016/j.ijrobp.2012.09.014 [DOI] [PubMed] [Google Scholar]
- 21. Harada K, Katoh N, Suzuki R, et al. Evaluation of the motion of lung tumors during stereotactic body radiation therapy (SBRT) with four‐dimensional computed tomography (4DCT) using real‐time tumor‐tracking radiotherapy system (RTRT). Phys Medica. 2016;32(2):305‐311. doi: 10.1016/j.ejmp.2015.10.093 [DOI] [PubMed] [Google Scholar]
- 22. Erridge SC, Seppenwoolde Y, Muller SH, et al. Portal imaging to assess set‐up errors, tumor motion and tumor shrinkage during conformal radiotherapy of non‐small cell lung cancer. Radiother Oncol. 2003;66(1):75‐85. doi: 10.1016/S0167-8140(02)00287-6 [DOI] [PubMed] [Google Scholar]
- 23. Rozendaal RA, Mijnheer BJ, Hamming‐Vrieze O, Mans A, Van Herk M. Impact of daily anatomical changes on EPID‐based in vivo dosimetry of VMAT treatments of head‐and‐neck cancer. Radiother Oncol. 2015;116(1):70‐74. doi: 10.1016/j.radonc.2015.05.020 [DOI] [PubMed] [Google Scholar]
- 24. Chen M, Yang J, Liao Z, et al. Anatomic change over the course of treatment for non‐small cell lung cancer patients and its impact on intensity‐modulated radiation therapy and passive‐scattering proton therapy deliveries. Radiat Oncol. 2020;15(1):1‐11. doi: 10.1186/s13014-020-01503-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Zhang P, Rimner A, Yorke E, et al. A geometric atlas to predict lung tumor shrinkage for radiotherapy treatment planning. Phys Med Biol. 2017;62(3):702‐714. doi: 10.1088/1361-6560/aa54f9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Kipritidis J, Hugo G, Weiss E, Williamson J, Keall PJ. Measuring interfraction and intrafraction lung function changes during radiation therapy using four‐dimensional cone beam CT ventilation imaging. Med Phys. 2015;42(3):1255‐1267. doi: 10.1118/1.4907991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Takao S, Miyamoto N, Matsuura T, et al. Intrafractional baseline shift or drift of lung tumor motion during gated radiation therapy with a real‐time tumor‐tracking system. Int J Radiat Oncol Biol Phys. 2016;94(1):172‐180. doi: 10.1016/j.ijrobp.2015.09.024 [DOI] [PubMed] [Google Scholar]
- 28. Mori S, Karube M, Shirai T, et al. Carbon‐ion pencil beam scanning treatment with gated markerless tumor tracking: an analysis of positional accuracy. Int J Radiat Oncol. 2016;95(1):258‐266. doi: 10.1016/j.ijrobp.2016.01.014 [DOI] [PubMed] [Google Scholar]
- 29. Mori S, Endo M. Comments on “Novel real‐time tumor‐contouring method using deep learning to prevent mistracking in X‐ray fluoroscopy” by Terunuma et al. Radiol Phys Technol. 2018;11(3):360‐361. doi: 10.1007/s12194-018-0447-4 [DOI] [PubMed] [Google Scholar]
- 30. Terunuma T, Sakae T. Response to “Comments on ‘Novel real‐time tumor‐contouring method using deep learning to prevent mistracking in X‐ray fluoroscopy’”. Radiol Phys Technol. 2018;11(3):362‐363. doi: 10.1007/s12194-018-0471-4 [DOI] [PubMed] [Google Scholar]
- 31. Sahiner B, Pezeshk A, Hadjiiski LM, et al. Deep learning in medical imaging and radiation therapy. Med Phys. 2019;46(1):e1‐e36. doi: 10.1002/mp.13264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. El Naqa I, Haider MA, Giger ML, Ten Haken RK. Artificial intelligence: reshaping the practice of radiological sciences in the 21st century. Br J Radiol. 2020;93(1106):20190855. doi: 10.1259/bjr.20190855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Zhao W, Shen L, Han B, et al. Markerless pancreatic tumor target localization enabled by deep learning. Int J Radiat Oncol Biol Phys. 2019;105(2):432‐439. doi: 10.1016/j.ijrobp.2019.05.071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Wei R, Zhou F, Liu B, et al. Real‐time tumor localization with single X‐ray projection at arbitrary gantry angles using a convolutional neural network (CNN). Phys Med Biol. 2020;65(6):065012. doi: 10.1088/1361-6560/ab66e4 [DOI] [PubMed] [Google Scholar]
- 35. Hirai R, Sakata Y, Tanizawa A, Mori S. Real‐time tumor tracking using fluoroscopic imaging with deep neural network analysis. Phys Medica. 2019;59(1):22‐29. doi: 10.1016/j.ejmp.2019.02.006 [DOI] [PubMed] [Google Scholar]
- 36. Terunuma T, Tomoda K, Sakae T, Ohnishi K, Okumura T, Sakurai H. [P266] Patient‐optimized deep learning for robust tumor tracking. Phys Medica. 2018;52(2):176. doi: 10.1016/j.ejmp.2018.06.545 [DOI] [Google Scholar]
- 37. Kirby N, Chuang C, Ueda U, Pouliot J. The need for application‐based adaptation of deformable image registration. Med Phys. 2013;40(1):011702. doi: 10.1118/1.4769114 [DOI] [PubMed] [Google Scholar]
- 38. Fukumitsu N, Nitta K, Terunuma T, et al. Registration error of the liver CT using deformable image registration of MIM Maestro and Velocity AI. BMC Med Imaging. 2017;17(1):30. doi: 10.1186/s12880-017-0202-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Shirotani T. Attenuation Coefficient of Human Tissues and Tissue Substitutes . JAERI; 1995. https://jopss.jaea.go.jp/pdfdata/JAERI‐Data‐Code‐95‐002.pdf
- 40. Ronneberger O, Fischer P, Brox T. U‐net: Convolutional Networks for Biomedical Image Segmentation . arXiv; 2015. https://arxiv.org/pdf/1505.04597.pdf
- 41. Kendall A, Badrinarayanan V, Cipolla R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder‐Decoder Architectures for Scene Understanding . arXiv; 2015. http://arxiv.org/abs/1511.02680
- 42. Jaccard P. Lois de distribution florale dans la zone alpine. Bull Soc Vaudoise Sci Nat. 1902;38:72. https://www.e‐periodica.ch/digbib/view?pid=bsv‐002:1902:38::503110 [Google Scholar]
- 43. Smith SL, Kindermans PJ, Ying C, Le QV. Don't Decay the Learning Rate, Increase the Batch Size. arXiv; 2017. https://arxiv.org/abs/1711.00489
- 44. Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D. Grad‐CAM: visual explanations from deep networks via gradient‐based localization. Int J Comput Vis. 2020;128(2):336‐359. doi: 10.1007/s11263-019-01228-7 [DOI] [Google Scholar]
- 45. Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the Hausdorff distance. IEEE Trans Pattern Anal Mach Intell. 1993;15(9):850‐863. doi: 10.1109/34.232073 [DOI] [Google Scholar]
- 46. Shen C, Nguyen D, Zhou Z, Jiang SB, Dong B, Jia X. An introduction to deep learning in medical physics: advantages, potential, and challenges. Phys Med Biol. 2020;65(5):05TR01. doi: 10.1088/1361-6560/ab6f51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Ridzuan F, Wan Zainon WMN. A review on data cleansing methods for big data. Procedia Comput Sci. 2019;161:731‐738. doi: 10.1016/j.procs.2019.11.177 [DOI] [Google Scholar]
- 48. Unberath M, Zaech J‐N, Lee SC, et al. DeepDRR–A Catalyst for Machine Learning in Fluoroscopy‐Guided Procedures . arXiv; 2018. https://arxiv.org/abs/1803.08606
- 49. Dhont J, Verellen D, Mollaert I, Vanreusel V, Vandemeulebroucke J. RealDRR–rendering of realistic digitally reconstructed radiographs using locally trained image‐to‐image translation. Radiother Oncol. 2020;153:213‐219. doi: 10.1016/j.radonc.2020.10.004 [DOI] [PubMed] [Google Scholar]
- 50. Shieh C‐C, Caillet V, Dunbar M, et al. A Bayesian approach for three‐dimensional markerless tumor tracking using kV imaging during lung radiotherapy. Phys Med Biol. 2017;62(8):3065‐3080. doi: 10.1088/1361-6560/aa6393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. de Bruin K, Dahele M, Mostafavi H, Slotman BJ, Verbakel WFAR. Markerless real‐time 3‐dimensional kV tracking of lung tumors during free breathing stereotactic radiation therapy. Adv Radiat Oncol. 2021;6(4):100705. doi: 10.1016/j.adro.2021.100705 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Remmerts de Vries IF, Dahele M, Mostafavi H, Slotman B, Verbakel W. Markerless 3D tumor tracking during single‐fraction free‐breathing 10MV flattening‐filter‐free stereotactic lung radiotherapy. Radiother Oncol. 2021;164:6‐12. doi: 10.1016/j.radonc.2021.08.025 [DOI] [PubMed] [Google Scholar]
- 53. Ying X, Guo H, Ma K, Wu J, Weng Z, Zheng Y. X2CT‐GAN: Reconstructing CT From Biplanar X‐rays with Generative Adversarial Networks . arXiv; 2019. https://arxiv.org/abs/1905.06902
- 54. Iramina H, Nakamura M, Mizowaki T. Direct measurement and correction of both megavoltage and kilovoltage scattered x‐rays for orthogonal kilovoltage imaging subsystems with dual flat panel detectors. J Appl Clin Med Phys. 2020;21(9):143‐154. doi: 10.1002/acm2.12986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Tashiro M, Kubota Y, Torikoshi M, Ohno T, Nakano T. Divided‐volume matching technique for volume displacement estimation of patient positioning in radiation therapy. Phys Medica. 2019;62:1‐12. doi: 10.1016/j.ejmp.2019.04.028 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are not available.


