Abstract
In this paper, a methodology is presented for managing hydrological ecosystem services by taking into account the hierarchy of stakeholders involved in the decision-making process. With this in mind, a water allocation model is first used for allocating water resources to demands. Then, several ecosystem services (ESs)-based criteria are defined to evaluate hydrological ESs of water resources management policies. A set of water and environmental resources management strategies (alternatives) are defined for decision-makers, and several drought management strategies are determined to decrease the area of key crops and water demands of agricultural nodes. To model a multi-agent multi-criteria decision-making problem for managing hydrological ESs, three main steps are considered as follows:
-
•
Different ES-based criteria (i.e., economic profit, NPP,1 and ecological index) are defined, and their grade-based values are estimated.
-
•
Several strategies are defined for stakeholders at different levels.
-
•
A recursive evidential reasoning (ER) approach, which considers a hierarchical structure for decision-makers and a leader-follower game, is used to select the best strategy for each decision-maker.
The applicability and efficiency of the methodology are illustrated by applying it to a real-world case study. The methodology is general and can be easily applied to other study areas.
Keywords: Group decision-making, Ecosystem services-based criteria, Hierarchical structure of stakeholders, Water resources management scenarios, Evidential reasoning
Method name: Multi-agent decision-making method to manage ecosystem services
Graphical abstract

Specifications table
| Subject area: | Engineering |
| More specific subject area: | Ecosystem Services Management |
| Name of your method: | Multi-agent decision-making method to manage ecosystem services |
| Name and reference of original method: | Behboudian, M., Kerachian, R., Motlaghzadeh, K., & Ashrafi, S. Evaluating water resources management scenarios considering the hierarchical structure of decision-makers and ecosystem services-based criteria. Science of the Total Environment, 751 (2021) 141759. https://doi.org/10.1016/j.scitotenv.2020.141759 |
| Resource availability: | It is advised that this approach be replicated using a simulation-optimization platform considering basin features and enhancing water-related ecosystem services (such as water delivery). Upon request, models and input data are made available. |
Related research article
Behboudian, M., Kerachian, R., Motlaghzadeh, K., and Ashrafi, S. Evaluating water resources management scenarios considering the hierarchical structure of decision-makers and ecosystem services-based criteria. Science of the Total Environment, 751 (2021) 141,759. https://doi.org/10.1016/j.scitotenv.2020.141759
Background
Population growth has increased urbanization and water and food demands [29], [35]. Ecosystems can produce water, food, and energy and provide benefits corresponding to human well-being. These types of benefits are referred to as ecosystem services (ESs) [1], [2], [3]. Several appropriate criteria should be taken into account to assess ESs. These criteria are selected depending on the available data [4]. In this study, only hydrological ESs are evaluated (i.e., water supply to the different water demand sectors and the ecological situation of the water-related system), mainly including the provisioning and regulating ESs. Maes et al. [5] presented a new methodology for assessing the land use effects on the number of water resources. They used a model developed for evaluating the impacts of land use in life cycle assessment (LCA). Mace et al. [6] assessed the relationships between biodiversity and ESs. In this research, biodiversity plays a crucial role in ecosystem service (i.e., regulating ESs). Additionally, some researchers have used numerical models such as SWAT2, InVEST3, etc, in environmental management, more specifically, ESs management [8], [30], [31], [36]. Karabulut et al. [7] evaluated different hydrological provisioning ESs regarding the nexus (water–food–energy, and ESs) using the SWAT simulation model. Also, Zarrineh et al. [1] investigated the different interrelations between ESs. They evaluated the existing land use conflicts in the study area and different scenarios by applying the SWAT model to the study area. Sahle et al. [8] quantitatively evaluated several water resources-based provisioning and regulating ESs using the InVEST model. They showed a large amount of sediment in the case study. Ashrafi et al. [2] introduced the concept of bankrupt ecosystems and used some bankruptcy methods to manage water-related ESs in such ecosystems. Ashrafi et al. [3] developed a comprehensive framework to evaluate the sustainability of provisioning, supporting, regulating, and cultural ESs in the Zarrinehrud basin, considering several climate change scenarios. They used the coupled SWAT-MODSIM model and experts’ viewpoints to evaluate the ESs under different climate change and water-related scenarios. Finally, they used a group decision-making method named COPRAS to choose an appropriate scenario. Behboudian et al. [23] analyzed the spatiotemporal variations of the resilience of ESs under extreme events in socio-hydrological systems. They enhanced the ES-based resilience of their study area by proposing several management scenarios.
Many researchers have recently applied several MCDM methods to making appropriate decisions in water and environmental problems [9], [37]. Weng et al. [10] used a synthesized decision support system with different water resource systems criteria. Madani and Lund [11] proposed a strategic non-cooperative game-theoretic framework to model MCDM problems. The Monte-Carlo game-theoretic approach has been considered to solve stochastic problems using multiple deterministic games. Finally, the proposed method could handle MCDM-based issues regarding several decision-makers and available uncertainties. Zhou et al. [12] addressed the application of the ER approach for MCDM problems with different agents by considering reliability and weights. According to this research, MCDM problems often include qualitative and quantitative criteria. Accordingly, the ER approach is a process that is suitable for dealing with existing uncertainties of such criteria. In this research, ER approach has led to a better consideration of uncertainty in the decision-making problem by involving concepts such as weight, reliability for decision-makers, and criteria. Tian et al. [13] developed a probabilistic MCDM method based on the ER approach that involves psychological preferences in decision-making. Optimism, pessimism, and neutrality were also considered ranking methods. Researchers used different methods to calculate the relative weight of criteria under uncertainty. The results indicated the appropriate performance of this method in collecting evaluations. Motlaghzadeh et al. [9] evaluated water and environmental resources management scenarios under climate change using a multi-agent decision-making framework. They used different games (i.e., Stackelberg and Bayesian games) to consider the hierarchical structure of decision-makers and their interactions. Table 1 presents the main characteristics of some relevant studies and compares them with the current work.
Table 1.
Reviewing the main characteristics of some relevant studies and comparing them with the current work.
| Researchers (year) | Title of work | Using Simulation-Optimization Models | Ecosystem Services Evaluation | Uncertainty Analysis | Selecting a preferable strategy using: |
Considering the Hierarchical Structure of Stakeholders | ||
|---|---|---|---|---|---|---|---|---|
| Multi-agent DM* methods | Multi-criteria DM methods | Game Theory | ||||||
| Karabulut et al. [7] | Mapping water provisioning services to support the ecosystem–water–food–energy nexus in the Danube river basin | ✓ | ✓ | – | – | – | – | – |
| Zhou et al. [12] | Evidential reasoning rule for MADM with both weights and reliabilities in group decision making | ✓ | – | ✓ | ✓ | ✓ | – | – |
| Sahle et al. [8] | Quantifying and mapping of water-related ecosystem services for enhancing the security of the food-water-energy nexus in tropical data–sparse catchment | ✓ | ✓ | – | – | – | – | – |
| Tian et al. [13] | Probabilistic linguistic multi-criteria decision-making based on evidential reasoning and combined ranking methods considering the decision-makers psychological preferences | ✓ | – | ✓ | ✓ | – | – | – |
| Ashrafi et al. [2] | Evaluating and improving the sustainability of ecosystem services in river basins under climate change | ✓ | ✓ | – | ✓ | ✓ | – | – |
| Current Paper | Application of Multi-Agent Decision-Making Methods in Hydrological Ecosystem Services Management | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Decision Making.
Reviewing the previous studies showed that the ES concept and its related criteria and sub-criteria have been considered in water resources systems’ evaluation without considering the decision maker's attitude and their power. Also, these studies have only evaluated limited ESs, leading to an imperfect understanding of extreme events and their consequences. Besides, the uncertainties of the evaluated ES-based criteria are not taken into account. Considering these drawbacks, several ES-based criteria, namely water resources-based provisioning ecosystem services (traditional resilience, reliability, and vulnerability); agricultural provisioning ES; the new carbon sequestration-related criterion (NPP4); ecological index; and agricultural profit are defined. Then, several WRM scenarios in terms of hydrological strategies are defined, and a leader-follower game-based ER approach is developed, which is the main contribution of this paper. In this approach, the hierarchical structure of stakeholders is considered to determine the preferable scenario regarding the role of central decision-makers, their power, and the available uncertainties of the mentioned criteria. This paper uses quantitative and qualitative criteria to promote the assessment's precision. In this regard, several ES-based criteria are considered in municipal, environmental, agricultural, and industrial sectors.
Method details
To manage the basin-wide hydrological ESs, several criteria are defined regarding different categories of ESs, and these types of ESs-based criteria are quantified. In the next step, several water-related strategies are defined, and the best strategy is prioritized and selected using a game theoretic methodology (Fig. 1).
Fig. 1.
A flowchart of the developed framework for assessing water-related scenarios using a game-theoretic evidential reasoning approach and considering ES-based criteria.
Data gathering
The time series of temporal variation of potential water resources such as surface water and groundwater and the time series of water demands such as municipal, environmental, and agricultural sectors should be gathered to evaluate the water-related ESs. Also, basic agricultural land information such as maximum water and crop yields, actual evapotranspiration, and agricultural crop profit is determined, which will be used in the simulation and optimization processes.
Defining water supply and demand management alternatives
The first step is discretizing the system into different sub-systems. Then, a class of drought levels should be defined at corresponding sub-systems based on their water resources [14]. The next step is determining several water supply and demand alternatives, which leads to estimating the optimal allocated water to existing demand sectors.
This paper recommends that readers use a simulation-optimization model to optimally allocate the available water resources in river basins regarding the defined drought conditions. To estimate water allocation, the water resources, and supply and demand alternatives should be specified at different sub-systems in the optimization period. Furthermore, water consumption in the demand nodes (municipal, industrial, agricultural, and environmental sectors) is needed.
Defining different drought management options
After defining water supply and demand alternatives, several drought management options corresponding to agricultural demand nodes are prescribed to reduce drought impacts in agricultural demand nodes. It should be mentioned that managing the agricultural sectors in this step is determined by reducing cultivated area by each management option and optimizing the corresponding allocated water to each dominant cropland at each option. To optimally allocate water resources between key crops, a two-level optimization model is used as follows:
Level 1: Determination of irrigation scheduling of the crops
This level optimally determines the total water consumption of major crops during the growing season concerning surface and groundwater resources. The objective function is described as follows:
| (1) |
where, and represent maximum crop yield (kg.ha−1) and actual crop yield. Also, and denote the maximum and actual evapotranspiration at the growth stages for crop i. Furthermore, S and Ks are the number of growth stages and the sensitivity coefficient of the ith crop at stage s to water shortage, respectively [15].
Level 2: Allocating water resources to major crops within a sub-system
After estimating and recursively optimizing the ratio of actual crop yield () to maximum crop yield () for each major crop, the following Eq. is taken into account to determine the optimal allocation of water for the different key crops within sub-systems.
| (2) |
where, , , and Profiti respectively denote the cultivated area of crops (ha), the performance function, and the profit of the ith crop. In order to determine the performance function regarding different water volumes, should be recursively estimated for significant crops.
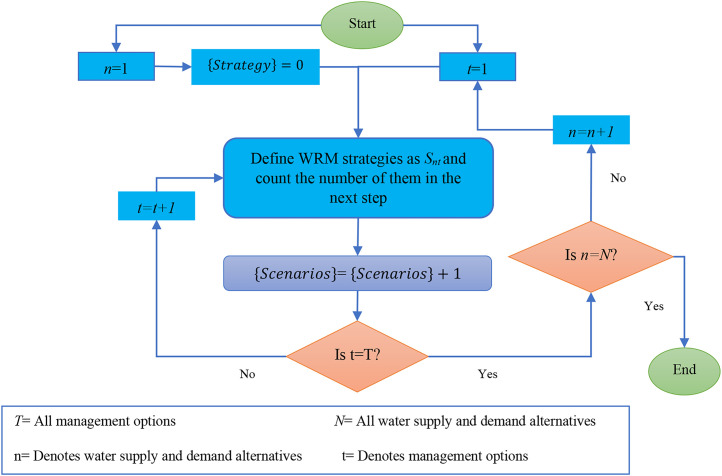
Defining water resources management (WRM) scenarios
As shown in Fig. 2, all combinations of the different alternatives (water supply and demand) and drought management options are defined as Water Resources Management (WRM)-related strategies.
Fig. 2.
Determining WRM scenarios.
Evaluating the ES-related criteria
In this research, several ES-based criteria are considered to evaluate different WRM-related strategies, and their weights should be estimated using approaches such as pair-wise comparison in the AHP approach. This method defines a comparison matrix from the viewpoint of each decision-maker, which assigns the preference numbers between attributes [16]. Three essential criteria, reliability, traditional resilience, and vulnerability, are considered to calculate water resources-based provisioning ESs for demand types, such as environmental and agricultural demand nodes. After quantifying the defined criteria, the grade values of these criteria are described.
In this paper, five grades (exclusive grades) are defined as the set of grades of assessment. These assessment grades’ numbers are determined considering the expected precision. Even distinct sets of assessment grades can be defined for various demand nodes or groups using the ER approach. However, before applying this approach, these disparate sets must be united [32]. In this study, all ES-based criteria, denoted in percentage intervals in Table 2, are evaluated using a set of evaluation grades with five mutually exclusive and collectively exhaustive grades.
Table 2.
Different grades with interval description.
| Grade's name | Definition | Description (%) |
|---|---|---|
| Worst | 0.0 ≤ Cr, Crs < 20 | |
| Poor | 20 ≤ Cr, Crs < 40 | |
| Average | 40 ≤ Cr, Crs < 60 | |
| Good | 60 ≤ Cr, Crs < 80 | |
| Best | 80 ≤ Cr, Crs < 100 |
Cr= Criterion; Crs= Sub-criterion.
A value between zero and one should be assigned to different grades (Hn), which denotes the belief degree of that grade of assessment. After defining this set of assessment grades, the water resources-based provisioning ESs are evaluated in different demand types considering three essential criteria. The grade values of these criteria (reliability, traditional resilience, and vulnerability- RRV critria) for each demand node are evaluated considering these grades and the coverage rate of water demand of that demand node. After assessing the RRV criteria of different nodes, their relative weights should be estimated to aggregate the grade values. Then, these grade values of the three criteria, as mentioned earlier, are recursively evaluated, and the grade-based water-related ES criterion is calculated. A similar process is used to calculate the grade-based values of the other ES-based criteria.
Let an MCDM problem with different decision-makers (D) contains M scenarios, sm (m = 1,…,M), K demand types (dk, k = 1,…,K), and L criteria (cl, l = 1,…,L). Moreover, N represents the number of assessment grades to evaluate ES-based criteria (). It is assumed that is preferred to.
| (3) |
Regarding these definitions, the assumed MCDM problem is modeled using Eq. (4) for criteria cl (l = 1,…,L) on demand dk (k = 1,…,K):
| (4) |
where and . represents a belief degree and an expectation for dk, and cl reads that a water demand node (dk) at a criterion (cl) is assessed to a grade with a belief degree of . The grade values of each criterion on each demand node (Dg) of Eq. (5) are indicated in the belief decision matrix. They are independently evaluated from the perspectives of several decision-makers:
| (5) |
Estimating the degree of beliefs
This paper uses quantitative and qualitative methods to evaluate all grade-based criteria (Fig. 3). To do this, appropriate grades of assessment are defined as Eq. (3). Then, the belief degrees of criteria are calculated using their temporal values or average value. In the case of the temporal time series of a criterion, the elements’ number is counted, and the degree of beliefs is calculated as follows:
| (6) |
where, denotes the degree of belief in grade for criterion . Also, and are planning horizon and the temporal values’ number of the criterion assigned to assessment grade , respectively. For an ES-based criterion with an average value, the corresponding degree of belief is calculated as follows:
| (7) |
Fig. 3.
Estimating the belief degrees for the ES-based criteria.
and are the average value of criterion and adjusted assessment grades for criterion , respectively. By taking into account the above-mentioned methods, the grade values of hydrological ES-based criteria are calculated. It should be noted that a numerical value between zero and 1.0 is assigned to each belief degree ().
Determining the weights
Determining the weights of criteria and their corresponding sub-criteria is crucial in aggregating grade values in the ER approach and affects the aggregated results. The weights of criteria and sub-criteria can be estimated by gathering experts’ viewpoints about the proper criteria weights or using other methods (e.g., pairwise comparison and ordered weighted averaging (OWA) methods). The difficulty of determining the relative weights is a weakness, which may affect the aggregation results because there are no unanimous ways of proposing the weights [32], [34].
Water provisioning ESs
As mentioned earlier, three performance criteria, reliability, vulnerability, and traditional resilience, are described to evaluate the provisioning of ESs. The reliability is the coverage proportion time series considering supplied water for different demand types during the planning time. Also, traditional resilience denotes the resilience of a system to absorb severe events’ impacts (i.e., droughts) and recover to a satisfactory situation. Furthermore, vulnerability represents the intensity of the failures during the simulation period. The reliability, vulnerability, and traditional resilience criteria are quantified regarding demand nodes. In the next step, the grade values of these criteria are calculated using the following equations. More details can be found in Behboodian and Kerachian [17] and Behboudian and Kerachian [20].
| (8) |
| (9) |
| (10) |
where, , , and represent the water provisioning criteria for the kth demand node at time step t, respectively. Also, and are the quantity of water optimally allocated to the demand node k at the tth time step and the temporal values of water demand to each demand node.
The normalized values of the grade values of the should be evaluated while taking into account the lowest and maximum amounts of this criterion for various demand nodes.
Agricultural-based provisioning ESs
To determine this criterion, the optimal water resources allotted to a major crop under WRM scenarios are compared to the typical situation in which all major crops' water requirements are met. Due to this, Eqs. (1) and (2) are used to compute the allocated water (mm/ha) for important crops and their farmed area (ha). In light of this, the following formula is used to compute the provisioning ES:
| (11) |
where, represents the agricultural provisioning ES for the ith crop in time step t at lth drought level. Furthermore, and are a cultivated area of crop i and the optimal allocated water. Also, and are allocated water and cultivated area of the crop i at normal condition N, respectively. The summation of the corresponding belief degrees should be equal to one.
Net primary productivity (NPP)
Plants capture and save solar energy through the photosynthesis process. In this process, the atmospheric carbon dioxide (CO2) would be converted to sugar molecules by living plants, which can be used as food. Also, the oxygen (O2) needed by humans to breathe is also provided. Therefore, in the process of photosynthesis, the O2 and the energy required by living existences on Earth are produced by plants. Since CO2 is a greenhouse gas, plants can mitigate global warming by absorbing the CO2 released from burning fossil fuels. The captured carbon by plants can become a part of their roots, leaves, stalks, tree trunks, etc.
The amount of net carbon dioxide (CO2) that a key crop captures throughout the photosynthetic and respiration processes is known as net primary productivity (NPP) [3], [18], [25], [27]. In order to calculate how much carbon is being collected by the main crops grown on agricultural land in the research area, this paper provides an NPP-based criterion. This criterion can appropriately take into account how various strategies affect the ecosystem under carbon balance. The following equation is employed to determine the amount of collected carbon by significant crops:
| (12) |
where, represents the captured carbon's amount in strategy j by ith crop (Kg.C year−1). Also, and are the optimal cultivated area (ha) of ith crop and the amount of the NPP () in WRM strategy j. For instance, the NPP of Wheat, Barely, Potato, and Tomato in northwestern Iran are respectively 3340.8, 3123.2, 3482,97, and 11,625.98 [3].
2-6-4- Ecological index
To quantify the ecological index of the system, this paper defines a criterion as follows:
| (13) |
where denotes the difference between the lake's average water volume and its acceptable water volume (ecological volume) of year t in the planning time. Also, and are ecological volume at tth year and the average annual volume, respectively.
To estimate , the temporal values of annual volume should be determined as follows:
| (14) |
where, , , and are the average volumes in the tth and t+1th years and the area in tth year, respectively. Moreover, , , , and denote annual inflow, net groundwater flow, evaporation, and precipitation from the surface area.
Economic and agricultural productivity
In order to estimate this ES-based criterion, the total allocated water resources (m3) for major crops is calculated. Then, the economic and agricultural productivity (profit/m3) of major crops is determined. Finally, the total agricultural profit is estimated by multiplying allocated water for each dominant crop and agricultural-economic productivity [26]. It should be noted that total agricultural profit should be determined in all sub-systems to calculate the final profit of the study area. Also, for all defined WRM strategies, this criterion is estimated as the seventh ES-based criterion. The following formula is used to calculate the agricultural profit of ith crop.
| (15) |
where denotes the agricultural profit for each WRM strategy. Also, and respectively are agricultural-economic productivity and the allocated water to major ith crop at jth sub-system in the planning time horizon. The summation of the corresponding belief degrees should be equal to one.
Evidential reasoning (ER) approach
The ER approach has been used substantially in multi-criteria decision analysis [38]. Some capabilities of the ER as a decision-making approach make it more promising and advantageous in environmental resources management problems: 1. Incorporating both quantitative and qualitative criteria; 2. Accounting for uncertain and incomplete assessments by experts; 3. Using an intuitive linguistic framework under which different criteria are assessed [14,16,17,19,[20], [21], [22], [23]].
The ER approach is used in this study to combine the ES-based criteria at various decision-making levels. The degree of the beliefs is converted into probability masses in the first phase by combining the weights and the degree of the beliefs.
| (16) |
| (17) |
where, denotes the basic probability masses for criterion l. Also, denotes unassigned remaining belief degrees. The ER approach incorporates this type of uncertainty (incomplete assessment) by assigning it to higher and lower evaluation classes. Moreover, is the weight for the lth criterion, in which the summation of the weights should be equal to 1 [21,22].
The probability masses are merged based on these criteria in the following step:
| (18) |
| (19) |
| (20) |
| (21) |
where denotes the combined basic probability masses and represents the degree of belief in the scenario for the grade .
A method for group decision-making using the leader-follower game
Hierarchy structure of the decision-makers
The key actors, the leaders, and the followers' acts, as well as their order of actions, are all included in the hierarchy structure of the decision-makers. The first step of this game is determining the leaders of the game. The leaders can make a decision or take action and also can influence how the game plays. In this regard, all possible actions of players are determined [33].
Given that decision-making challenges involve a variety of diverse decision-makers, a thorough analysis is required to identify the most correlated leaders and followers and, ultimately, the optimum game structure. These games are divided into four categories: perfect or imperfect games, complete or incomplete games, static and dynamic games, and finite and infinite games. The first game measures the players' familiarity with the various player rewards. The second and third games are connected to the number of games and, respectively, the players' awareness of other players' prior actions. Finally, the finite and infinite games represent the number of possible actions that all players could take. There are also two other forms of categorizing this game which has named extensive and normal games [28].
This paper has found an extensive complete game best fitting for the existing decision-making problem. In other words, there are two different levels of players who do not act concurrently. The complex game depicts the precise sequences in which the players carry out their actions. In this type of game, the players, their actions, and the appropriate time for taking these actions are easily understood. In case there is a sequence in making a decision or, in other words, all players are not taking their actions simultaneously, the proposed game is a leader-follower game.
A player who plays as the leader makes decisions before the follower does. The leaders can easily predict the results of other players' actions once they are aware of the payoff of other players (the game is a complete game), and this type of game will aid them in taking the desired action. As seen in Fig. 4, a bi-level game has levels for leaders and followers.
Fig. 4.
A two-level game hierarchy [15].
Players at the same level behave similarly based on the level's collective decision-making. All game situations are available depending on the different ways the player can combine their actions. As an instance, if player A has two actions (A1 and A2), and player B has two actions (B1 and B2), the possible scenarios are {A1B1, A1B2, A2B1, A2B2}. After the players' statuses and actions are determined, the structure of the game and formed scenarios are determined.
Estimating the relative weights
The relative weights for each level of players are estimated concerning the summation of weights at each level should equal one. The relative significance of ES-based criteria is then assessed in relation to players' perceptions. This paper suggests accumulating the expert's opinions to determine the importance of criteria for each player. Regarding the AHP methodology, the pair-wise comparison method can also be utilized to estimate the relative weights of the criteria.
Calculating the payoff of players
This step uses the degree of beliefs (βn), which can be calculated using the ER approach. First, utility value (Uk) is assigned to grades of assessment (H1…Hn). Next, the strategies’ payoffs are determined for all players as follows:
| (22) |
| (23) |
where j indicates the number of strategies and i the number of hierarchy levels. Additionally, k denotes the number of assessment grades. It should be noted that i = 1 and i = 2 are assigned for leaders and followers, respectively.
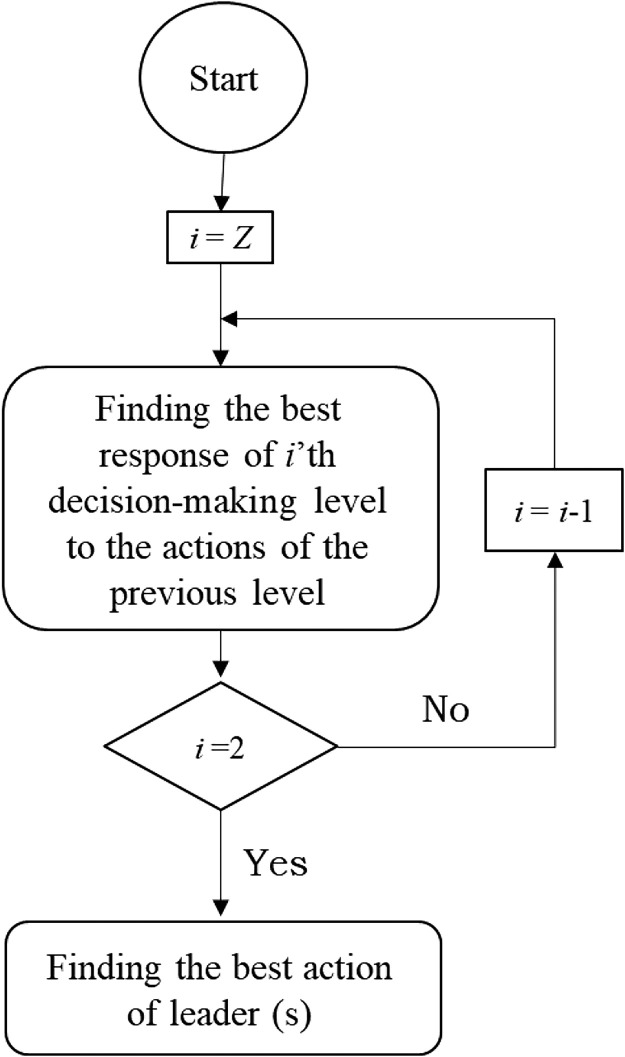
Backward induction (BI) method
This paper's leader-follower game can be solved using the backward induction method. This approach is typically used to resolve games involving logical players. By selecting the appropriate actions that produce the greatest number of payoffs, these players aim to increase their payoff.
Regarding the fact that leaders completely know the reactions of the lower-level players (followers) to their actions, this rule is used to help them choose their best action in the BI method. This process has three main steps in two-level leader-follower games as follows:
-
•
Determining the optimum follower responses to each leader's action.
-
•
Finding the optimal course of action for leaders while taking into account the best follower reactions identified in the previous step.
-
•
The extensive game's equilibrium solution should be discovered in the third step.
In the final two steps of the BI method, players compare all of their possible actions, taking into account the payoffs they could receive from doing so, and select the action with the highest possible payoff quantity. This algorithm is represented in Fig. 5. More detail and information can be found in Aumann [24].
Fig. 5.
A flowchart of the Backward Induction (BI) algorithm [24].
Selecting the preferable strategy regarding the ES-based criteria
After optimal water allocation for available demand types at each sub-system, the criteria' grade values should be calculated. Firstly, the ER approach calculates each sub-system's aggregated grade values of water provisioning criteria. The grade values of all sub-system criteria are synthesized using the ER approach in the second stage. The aggregated values of the system are then utilized to produce water resource-based provisioning ESs for all options.
The number of decision-makers is determined, and the leaders and followers are specified after quantifying each strategy's grade values of criteria. Finally, water resources management strategies are compared, and the preferred strategy is selected considering the proposed framework and the players' payoffs (leaders and followers) (Fig. 6).
Fig. 6.
Employing the proposed methodology for determining the best WRM scenario(s).
For instance, three key stakeholders in the Urmia Lake Basin (ZRB) are involved in the decision-making process for selecting the preferred WRM method. Leaders who can offer various approaches to managing water supply demand include the Urmia Lake restoration national committee (ULRNC) and Iran's regional water company (IRWC).
The first management alternative is to fully allocate the water demand for Urmia Lake (UL1). Decreasing the allocated water to the lake by up to 35% is the second management alternative (UL2). Tables 3 and 4 present two main alternatives and five drought levels. After selecting an action (one of the alternatives) by the leaders, it is reported to the single follower of the game, Iran's Ministry of Agriculture Jihad (IMAJ). This follower has its own actions (agricultural drought management options). These options are reducing the cultivated area of the major crop (AG1), reducing the variety of major crops (AG2), and eliminating some agricultural cultivated areas considering the amount of allocated water to the agricultural sector (AG3).
Table 3.
Alternatives of water allocation to Urmia Lake [14].
| Alternative | Description | Assumption |
|---|---|---|
| UL1 | Distributing as much as possible of the 3100 million m3 of annual water rights from Urmia Lake | Except in extreme droughts, Urmia Lake's complete annual water right is delivered. |
| UL2 | In extremely severe droughts, Urmia Lake's annual water demand is reduced by 35% (or 1085 million m3) (Level 4 in Table (3)) | In normal conditions, the water SDR* in the agricultural sector is not increased to offset a deficiency in supplying the water demand of Urmia Lake in past periods |
Supply-to-Demand Ratio.
Table 4.
Different drought levels and their description.
| Drought level | Water allocation approach | Definition of water allocation to demands |
|---|---|---|
| 0 | Normal condition | All water demands are entirely supplied. |
| 1 | Water conservation condition | A low-level drought has occurred, and water demands are not entirely supplied in demand nodes with low priorities. |
| 2 | An average drought | A water allocation to demand nodes with low priorities is more constrained (i.e., partial water allocation to agricultural demands). |
| 3 | A severe drought | |
| 4 | An extreme drought | Water allocation to demand nodes with low priorities is constrained as much as possible. |
Considering the IMAJ as a single follower, the problem was modeled in this study area by a two-level game (leader-follower game). In this game, leaders (ULRNC and IRWC) can choose two alternatives (UL1 or UL2), and IMAJ can also select three agricultural-based options (AG1, AG2, and AG3). With this in mind, six strategies are presented in Fig. 7.
| (24) |
Fig. 7.
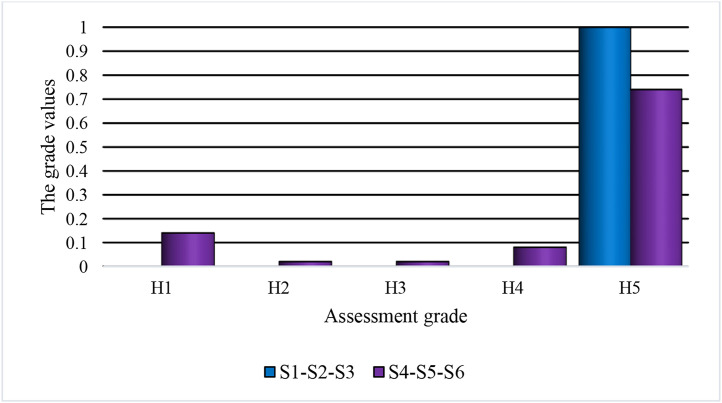
The grade-based results of the ecological index in all strategies.
Regarding the existence of two players in the first level of the game, the players' weights should be estimated. In this example, it is assumed that both leaders have the same relative weights (0.5, 0.5) because of their higher influencing authority. Because of existing just one follower (IMJA), its weight should equal 1.0.
There are seven important criteria in this example by which the players evaluate the strategies. The reliability, traditional resilience, and vulnerability criteria were synthesized using the ER approach for each strategy. The other criteria are the NPP-based criterion, agricultural profit, agricultural provisioning ESs, and the Urmia Lake's ecological index. Therefore, five important criteria were used in the selected basin.
The values of agricultural provisioning ESs in different strategies have been calculated considering the optimal allocated water to major crops. The grade values for the main crops in sub-systems were aggregated using the ER approach to assess this criterion. The pair-wise comparison method was employed to calculate the relative weight of the major crops for various players and sub-systems. Moreover, the evaluation of the players' organizational roles and interests has been based on the profit per cubic meter of allocated water (U.S. $/m3), values of water requirements (mm/ha), and the profit per hectare (U.S. $/ha) for all three players in the game (IRWC, ULRNC, and IMJA).
According to the total areas of agricultural lands in the research region, the weights of the sub-systems and available provinces have been estimated, which is an appropriate measure of their relative importance. For instance, expert opinions were used to estimate the relative weights of ES-based criteria, and the specifics of this estimation process are shown in Table 5.
Table 5.
The level of importance (LI), numerical values (NV), group weights (GW), and group importance (GI) of all criteria in decision makers' viewpoint.
| ES-based Criteria | Experts |
GI | GW | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| First Expert |
Second Expert |
Third expert |
Forth expert |
|||||||
| LI | NV | LI | NV | LI | NV | LI | NV | |||
| NCULR | ||||||||||
| Reliability | Highb | 0.8 | a | 1.0 | b | 0.8 | c | 0.5 | 0.78 | 0.22 |
| Traditional Resilience | b | 0.8 | b | 0.8 | b | 0.8 | c | 0.5 | 0.74 | 0.22 |
| Vulnerability | b | 0.8 | a | 1.0 | b | 0.8 | c | 0.5 | 0.78 | 0.21 |
| NPP | Lowd | 0.2 | b | 0.8 | c | 0.5 | c | 0.5 | 0.44 | 0.04 |
| APES* | b | 0.8 | d | 0.2 | d | 0.2 | d | 0.2 | 0.5 | 0.08 |
| EI⁎⁎ | Very higha | 1.0 | a | 1.0 | b | 0.8 | a | 1.0 | 1.0 | 0.18 |
| AP⁎⁎⁎ | Averagec | 0.5 | c | 0.5 | c | 0.5 | c | 0.5 | 0.5 | 0.04 |
| IRWC | ||||||||||
| Reliability | a | 1.0 | a | 1.0 | a | 1.0 | a | 1.0 | 1.0 | 0.16 |
| Traditional Resilience | a | 1.0 | a | 1.0 | a | 1.0 | a | 1.0 | 1.0 | 0.16 |
| Vulnerability | a | 1.0 | a | 1.0 | a | 1.0 | b | 0.8 | 0.96 | 0.16 |
| NPP | d | 0.2 | d | 0.2 | d | 0.2 | Very lowe | 0.0 | 0.16 | 0.09 |
| PESA | c | 0.5 | d | 0.2 | d | 0.2 | c | 0.5 | 0.38 | 0.11 |
| EC | b | 0.8 | b | 0.8 | b | 0.8 | b | 0.8 | 0.8 | 0.21 |
| AP | d | 0.2 | d | 0.2 | d | 0.2 | d | 0.2 | 0.2 | 0.11 |
| IMAJ | ||||||||||
| Reliability | a | 1.0 | c | 0.5 | c | 0.5 | b | 0.8 | 0.82 | 0.15 |
| Traditional Resilience | a | 1.0 | c | 0.5 | c | 0.5 | b | 0.8 | 0.76 | 0.14 |
| Vulnerability | a | 1.0 | c | 0.5 | c | 0.5 | b | 0.8 | 0.76 | 0.14 |
| NPP | c | 0.5 | b | 0.8 | a | 1.0 | b | 0.8 | 0.72 | 0.13 |
| PESA | a | 1.0 | a | 1.0 | a | 1.0 | a | 0.5 | 1.0 | 0.18 |
| EC | c | 0.5 | c | 0.5 | c | 0.5 | c | 0.5 | 0.5 | 0.09 |
| AP | a | 1.0 | a | 1.0 | a | 1.0 | a | 1.0 | 1.0 | 0.18 |
a) Very high; b) High; c) Average; d) Low; e) Very low.
APES= Agricultural Provisioning Ecosystem Services.
EI= Ecological Index.
AP= Agricultural productivity.
Also, Tables 6 and 7 respectively present the grade values of provisioning ESs criteria (traditional resilience, reliability, and vulnerability) for several sub-systems corresponding to ULRNC in the first scenario (S1) and the grade-based assessment of the APES criterion in scenario S1 from the point of view of IMAJ as an example. Furthermore, Fig. 7 presents the schematic view of grade values of an important ES-based criterion (ecological index) as an example.
Table 6.
The grade values of water-related provisioning ES criteria from the viewpoint of ULRNC in scenario S1.
| Sub-system | Criterion | Grade-based Value |
||||
|---|---|---|---|---|---|---|
| Aji Chai-upstream | Rel | 0.03 | 0 | 0.01 | 0.01 | 0.95 |
| Res | 0.03 | 0 | 0 | 0.01 | 0.96 | |
| Vul | 0.06 | 0 | 0.02 | 0.01 | 0.91 | |
| Aji Chai-downstream | Rel | 0 | 0.01 | 0.04 | 0.04 | 0.91 |
| Res | 0.06 | 0 | 0 | 0 | 0.94 | |
| Vul | 0.02 | 0.04 | 0 | 0.04 | 0.90 | |
| Sufi Chai-upstream | Rel | 0 | 0 | 0.07 | 0 | 0.93 |
| Res | 0.07 | 0 | 0.01 | 0 | 0.92 | |
| Vul | 0.19 | 0 | 0 | 0.02 | 0.79 | |
| Sufi Chai-downstream | Rel | 0 | 0 | 0 | 0.05 | 0.95 |
| Res | 0.04 | 0 | 0 | 0 | 0.96 | |
| Vul | 0.01 | 0.01 | 0.03 | 0 | 0.95 | |
| Other | Rel | 0 | 0.03 | 0.2 | 0.28 | 0.49 |
| Res | 0.27 | 0.01 | 0 | 0 | 0.72 | |
| Vul | 0.34 | 0.03 | 0 | 0.03 | 0.60 | |
*Rel: Reliability; **Res: Resiliency; ***Vul: Vulnerability.
Table 7.
The grade-based assessment of the APES criterion in scenario S1 (from the IMAJ viewpoint).
| Province | Assessment grades |
||||
|---|---|---|---|---|---|
| H1 | H2 | H3 | H4 | H5 | |
| East Azerbaijan | 0.21 | 0.07 | 0.01 | 0.01 | 0.7 |
| West Azerbaijan | 0.36 | 0.03 | 0 | 0 | 0.61 |
| Kurdistan | 0.19 | 0 | 0.04 | 0.04 | 0.72 |
The payoffs for the leaders and the single follower in a two-level game were determined using the computed grade values. In the original research paper, the ER approach is used to assign five grades of assessment, resulting in five different utility values. The utility values for the grades of assessment H1, H2, H3, H4, and H5 in this study are 0.2, 0.4, 0.6, 0.8, and 1.0, respectively.
After determining the primary players, their actions, and required relative weights, the most desired responses of a single follower were found. When the leaders pick UL1 or UL2, as seen in Fig. 8, IMAJ selects AG1. Regarding these actions, strategies S1 and S4 are selected with the highest payoffs. Therefore, the leaders select UL1 or UL2, which led to strategies S1 or S4, to determine the preferred action. In this case, the leaders chose UL1 because S1 offered them greater payoffs. Finally, the followers adopt strategy AG1, and the equilibrium solution is S1.
Fig. 8.
Process of solving the extensive game by applying the BI method [14].
Discussion
Climate change and inappropriate management of water resources have created many challenges for water resources in many parts of the world. These problems have manifested in many areas in the form of land subsidence, drop in water level in lakes, drying up of water wells, and decrease in the production of agricultural products. In this paper, a methodology was proposed for evaluating basin-scale areas from the perspective of hydrological ecosystem services. With this in mind, in this paper, seven hydrological ES-based criteria, which include the main aspects of basin-wide ecosystem services, were proposed. Then, for the management of hydrological ecosystem services in the basin, a set of management strategies was defined that mainly deal with water management in the agricultural sector. In addition, agents and their preferences were considered to incorporate the social and intuitional dimensions of the problem. The agents in the case study of this paper formed a bi-level game where decisions are taken sequentially. The agents’ payoffs were also calculated using the evidential reasoning approach, capturing different criteria that seem crucial from the agents’ perspective.
To prioritize and determine the preferable scenarios (equilibriums of the game), the bi-level extensive game was solved by applying the backward induction method. The results of using this methodology in the Lake Urmia basin demonstrated that the leaders' best alternative is fully allocating Lake Urmia's water need with the highest payoff of 0.96. Additionally, with a payoff of 0.84, the agricultural management option related to decreasing the cultivated area is selected as the best action of the single follower.
As the decision-making model has a relatively complex structure, at first, its sub-models have been validated. Because a model with completely similar assumptions was not available, to validate the overall model, the results of the model were evaluated and verified in extreme conditions. The proposed game-based framework for evaluating the hydrological ecosystem services is general and can be easily applied to other study areas. Although the methodology proposed in this paper can be used for multi-agent decision-making in the management of hydrological ecosystem services, its results can be affected by the uncertainty in the inputs and parameters of the models. This issue is one of the most important limitations of the proposed methodology.
In the current methodology, some uncertainties are considered implicitly through long-term simulation of strategies or by the capabilities of the ER approach. However, it is recommended that the current methodology be extended so that it can explicitly consider the existing uncertainties. To evaluate the groundwater-based hydrological ecosystem services, some appropriate models, such as MODFLOW or SWAT-MODFLOW, would be utilized in future studies.
CRediT authorship contribution statement
Massoud Behboudian: Conceptualization, Methodology, Software, Writing – original draft. Reza Kerachian: Supervision, Validation, Methodology, Writing – review & editing. Kasra Motlaghzadeh: Conceptualization, Methodology, Software, Writing – original draft. Saeed Ashrafi: Methodology, Software, Writing – original draft.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Soil and Water Assessment Tool
Integrated Valuation of Ecosystem Services and Trade-offs
Net Primary Productivity
Net Primary Productivity
Data availability
Data will be made available on request.
References
- 1.Zarrineh N., Abbaspour K.C., Van Griensven A., Jeangros B., Holzkämper A. Model-based evaluation of land management strategies with regard to multiple ecosystem services. Sustainability. 2018;10(11):3844. [Google Scholar]
- 2.Ashrafi S., Mohammadpour Khoie M.M., Kerachian R., Shafiee-Jood M. Managing basin-wide ecosystem services using the bankruptcy theory. Sci. Total Environ. 2022;842 doi: 10.1016/j.scitotenv.2022.156845. [DOI] [PubMed] [Google Scholar]
- 3.Ashrafi S., Kerachian R., Pourmoghim P., Behboudian M., Motlaghzadeh K. Evaluating and improving the sustainability of ecosystem services in river basins under climate change. Sci. Total Environ. 2022;806 doi: 10.1016/j.scitotenv.2021.150702. [DOI] [PubMed] [Google Scholar]
- 4.Kandziora M., Burkhard B., Müller F. Interactions of ecosystem properties, ecosystem integrity and ecosystem service indicators - a theoretical matrix exercise. Ecol. Indic. 2013;28:54–78. [Google Scholar]
- 5.Maes W.H., Heuvelmans G., Muys B. Assessment of land use impact on water-related ecosystem services capturing the integrated terrestrial− aquatic system. Environ. Sci. Technol. 2009;43(19):7324–7330. doi: 10.1021/es900613w. [DOI] [PubMed] [Google Scholar]
- 6.Mace G.M., Norris K., Fitter A.H. Biodiversity and ecosystem services: a multilayered relationship. Trends Ecol. Evol. 2012;27(1):19–26. doi: 10.1016/j.tree.2011.08.006. Amst. [DOI] [PubMed] [Google Scholar]
- 7.Karabulut A., Egoh B.N., Lanzanova D., Grizzetti B., Bidoglio G., Pagliero L., Bouraoui F., Aloe A., Reynaud A., Maes J., Vandecasteele I., Mubareka S. Mapping water provisioning services to support the ecosystem–water–food–energy nexus in the Danube river basin. Ecosyst. Serv. 2016;17:278–292. [Google Scholar]
- 8.Sahle M., Saito O., Fürst C., Yeshitela K. Quantifying and mapping of water-related ecosystem services for enhancing the security of the food-water-energy nexus in tropical data–sparse catchment. Sci. Total Environ. 2019;646:573–586. doi: 10.1016/j.scitotenv.2018.07.347. [DOI] [PubMed] [Google Scholar]
- 9.Motlaghzadeh K., Eyni A., Behboudian M., Pourmoghim P., Ashrafi S., Kerachian R., Hipel K.W. A multi-agent decision-making framework for evaluating water and environmental resources management scenarios under climate change. Sci. Total Environ. 2023;864 doi: 10.1016/j.scitotenv.2022.161060. [DOI] [PubMed] [Google Scholar]
- 10.Weng S.Q., Huang G.H., Li Y.P. An integrated scenario-based multi-criteria decision support system for water resources management and planning–a case study in the Haihe River Basin. Expert Syst. Appl. 2010;37(12):8242–8254. [Google Scholar]
- 11.Madani K., Lund J.R. A Monte-Carlo game theoretic approach for multi-criteria decision making under uncertainty. Adv. Water Resour. 2011;34(5):607–616. [Google Scholar]
- 12.Zhou M., Liu X.B., Chen Y.W., Yang J.B. Evidential reasoning rule for MADM with both weights and reliabilities in group decision making. Knowl. Based Syst. 2018;143:142–161. doi: 10.1016/j.knosys.2017.12.013. [DOI] [Google Scholar]
- 13.Tian Z.P., Nie R.X., Wang J.Q. Probabilistic linguistic multi-criteria decision-making based on evidential reasoning and combined ranking methods considering decision-makers’ psychological preferences. J. Oper. Res. Soc. 2020;71(5):700–717. [Google Scholar]
- 14.Behboudian M., Kerachian R., Motlaghzadeh K., Ashrafi S. Evaluating water resources management scenarios considering the hierarchical structure of decision-makers and ecosystem services-based criteria. Sci. Total Environ. 2021;751 doi: 10.1016/j.scitotenv.2020.141759. [DOI] [PubMed] [Google Scholar]
- 15.Behboudian M., Kerachian R., Pourmoghim P. Evaluating the long-term resilience of water resources systems: application of a generalized grade-based combination approach. Sci. Total Environ. 2021;786 [Google Scholar]
- 16.Akhoundi A., Nazif S. Sustainability assessment of wastewater reuse alternatives using the evidential reasoning approach. J. Clean. Prod. 2018;195:1350–1376. [Google Scholar]
- 17.Behboodian M., Kerachian R. Sustainability assessment of basin-wide water supply and demand scenarios using intelligent decision system (IDS) model. Iran Water Resour. Res. 2020;15(4):316–329. (In Persian) [Google Scholar]
- 18.Vargas L., Willemen L., Hein L. Assessing the capacity of ecosystems to supply ecosystem services using remote sensing and an ecosystem accounting approach. Environ. Manag. 2019;63(1):1–15. doi: 10.1007/s00267-018-1110-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Motlaghzadeh K., Kerachian R., Tavvafi A. An evidential reasoning-based leader-follower game for hierarchical multi-agent decision making under uncertainty. J. Hydrol. 2020;591 Amst. [Google Scholar]
- 20.Behboudian M., Kerachian R. Evaluating the resilience of water resources management scenarios using the evidential reasoning approach: the Zarrinehrud river basin experience. J. Environ. Manag. 2021;284 doi: 10.1016/j.jenvman.2021.112025. [DOI] [PubMed] [Google Scholar]
- 21.Behboudian M., Kerachian R., Mahjouri N. Evaluating the resilience of water resources management projects in river basins considering stakeholder’s characteristics. Iran Water Resour. Res. 2022;18(1):180–207. (In Persian) [Google Scholar]
- 22.Pourmoghim P., Behboudian M., Kerachian R. An uncertainty-based framework for evaluating and improving the long-term resilience of lakes under anthropogenic droughts. J. Environ. Manag. 2022;301 doi: 10.1016/j.jenvman.2021.113900. [DOI] [PubMed] [Google Scholar]
- 23.Behboudian M., Anamaghi S., Mahjouri N., Kerachian R. Enhancing the resilience of ecosystem services under extreme events in socio-hydrological systems: a spatio-temporal analysis. J. Clean. Prod. 2023;397:136437. [Google Scholar]
- 24.Aumann R.J. Backward induction and common knowledge of rationality. Games Econ. Behav. 1995;8(1):6–19. [Google Scholar]
- 25.Civeira G. Potential changes in net primary productivity and carbon input of periurban agroecosystems treated with biosolids in Buenos Aires, Argentina. Pedosphere. 2016;26(1):98–107. [Google Scholar]
- 26.Emami F. Faculty of Civil and Environmental Engineering, University of Kassel; Germany: 2018. Hydro-economic modeling for optimization of sustainable water management of a river basin in the wake of climate change: Case study of the Zarrine River basin (ZRB), Iran. Ph.D. Thesis. [Google Scholar]
- 27.Koga N., Smith P., Yeluripati J.B., Shirato Y., Kimura S.D., Nemoto M. Estimating net primary production and annual plant carbon inputs, and modelling future changes in soil carbon stocks in arable farmlands of northern Japan. Agric. Ecosyst. Environ. 2011;144(1):51–60. [Google Scholar]
- 28.Osborne M.J. Vol. 3. Oxford university press; New York: 2004. (An Introduction to Game Theory). [Google Scholar]
- 29.Nguyen B.Q., Tran T.N.D., Łukaszewska M.G., Sinicyn G., Lakshmi V. Assessment of urbanization-induced land-use change and its impact on temperature, evaporation, and humidity in central Vietnam. Water. 2022;14(21):3367. [Google Scholar]
- 30.Tran T.N.D., Nguyen B.Q., Zhang R., Aryal A., Łukaszewska M.G., Sinicyn G., Lakshmi V. Quantification of Gridded Precipitation Products for the Streamflow Simulation on the Mekong River Basin Using Rainfall Assessment Framework: A Case Study for the Srepok River Subbasin, Central Highland Vietnam. Remote Sens. 2023;15(4):1030. [Google Scholar]
- 31.T.N.D. Tran, B.Q. Nguyen, N.D. Vo, M.H. Le, Q.D. Nguyen, V. Lakshmi, J. Bolten, Quantification of global digital elevation model (DEM) – A case study of the newly released NASADEM for a river basin in central Vietnam, J. Hydrol. Reg. Stud. 45 (2023b) 101282.
- 32.Jahanshahi S., Kerachian R. An evidential reasoning-based sustainability index for water resources management. Hydrological Sciences Journal. 2019;64(10):1223–1239. [Google Scholar]
- 33.Jahanshahi S., Kerachian R., Emamjomehzadeh O. A leader-follower framework for sustainable water pricing and allocation. Water Resources Management. 2023;37:1257–1274. [Google Scholar]
- 34.Behboudian M., Kerachian R., Hosseini M. Application of information fusion techniques and satellite products in the optimal redesign of rain gauge networks. Stochastic Environmental Research and Risk Assessment. 2021;35:1665–1680. [Google Scholar]
- 35.Sahebzadeh A., Kerachian R., Mohabbat H.R., Ashrafi S. Developing a framework for water right allocation in inter-basin water transfer systems under uncertainty: the Solakan–Rafsanjan water transfer experience. International Water Association (IWA) - Water Supply. 2020;20(7):2658–2681. [Google Scholar]
- 36.Karamouz M., Teymoori J., Olyaei M.A. A Spatial non-stationary based site selection of artificial groundwater recharge: a case study for semi-arid regions. Water Resour Manage. 2021;35:963–978. doi: 10.1007/s11269-020-02762-7. [DOI] [Google Scholar]
- 37.Karamouz M., Teymori J., Rahimi R., Olyaei M.A., Mohammadpour P. World Environmental and Water Resources Congress 2018: Groundwater, Sustainability, and Hydro-Climate/Climate Change. American Society of Civil Engineers; Reston, VA: 2018. . The impact of artificial groundwater recharge on water resources sustainability; pp. 92–102. [Google Scholar]
- 38.A. Abed-Elmdoust, R. Kerachian. Assessment of industrial solid waste using the intelligent decision system (IDS) method. Environmental Engineering & Management Journal (EEMJ) 15 (8) (2016) 1789-1800.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.