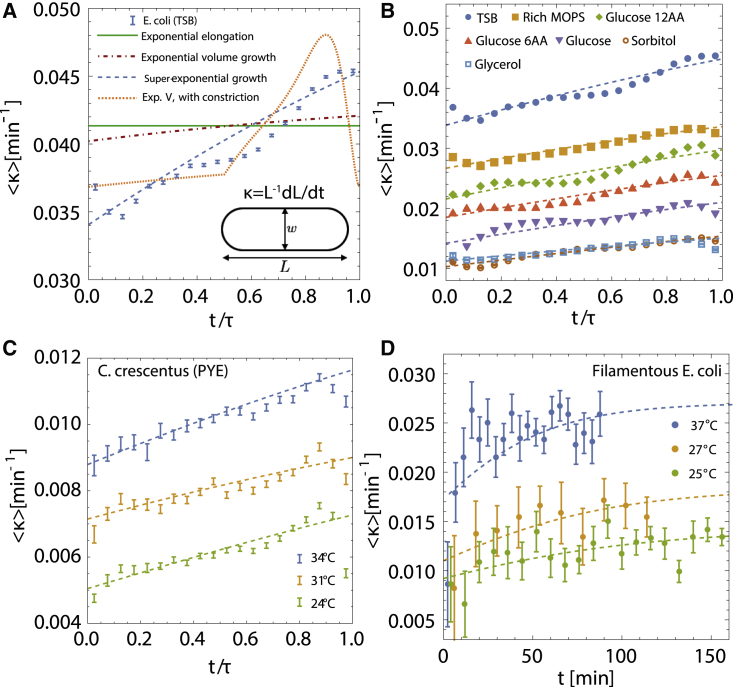
Figure 1.

Super-exponential growth in E. coli and C. crescentus cells in different conditions. (A) Ensemble-averaged instantaneous growth rate of E. coli cells grown in tryptic soy broth (TSB) media at $37°\mathrm{C}$ versus normalized time $t/\tau$, where τ is cell-cycle duration. Data are taken from (4). Error bars in all parts show $\pm$ 1 standard error of the mean. The solid green line shows a fit of exponential length growth Eq. 1, dot-dashed red line represents a prediction from exponential volume growth Eq. 2, dashed blue curve shows a fit to the super-exponential growth model Eq. 3, and the dotted orange curve shows fit to exponential volume growth model with constriction dynamics. Fitting parameters: model 1: $L_0=3.87\mu$m, $\kappa =0.041$ min${}^{-1}$; model 2: $L=3.89\mu$m, $k_V=0.044$ min${}^{-1}$; model 2 with constriction: $L_0=3.87\mu$m, $k_V=0.04$ min${}^{-1}$; model 3: $L_0=3.99\mu$m, $k=0.057$ min${}^{-1}$, $\lambda =1.59\mu$m. Cell width ($w=0.98\mu$m) value is taken directly from experimental data. Inset: a simplified cell shape schematic for E. coli, defining the size parameters. (B) Fits of super-exponential growth model Eq. 3 to average growth rate data for seven different growth conditions grown at $37°\mathrm{C}$, taken from (4). Error bars are negligible on the plotted scale. The values of k and λ for each condition are provided in Fig. 2B. (C) Fits of the super-exponential growth model Eq. 3 to average instantaneous growth rate versus $t/\tau$ of C. crescentus cells grown in PYE at three different temperatures. Data are taken from (11). (D) Time-dependent growth rate in filamentous E. coli cells grown in LB at different temperatures, presented in absolute time. Data are taken from (6). Dashed lines in (A)–(D) represent fits of the model in Eq. 3. To see this figure in color, go online.