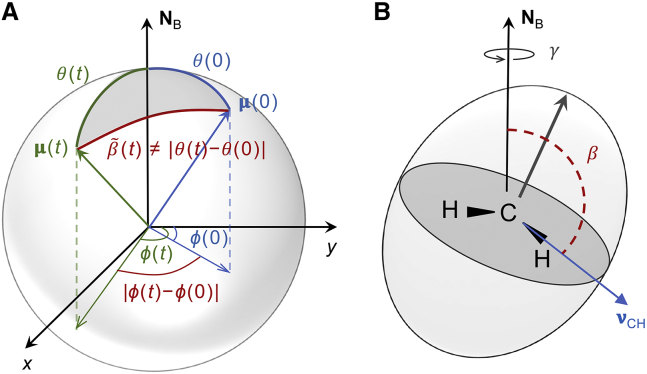
Figure 8.

Schematic illustration of angles used in different approaches for analyzing CH bond fluctuations from MD simulations. (A) Spherical-harmonic representation of the orientation of the CH bond at t = $0$ and time $t$ described by unit vector $\mathbf{\mu }\left(0\right)$ and unit vector $\mathbf{\mu }\left(t\right)$. The corresponding spherical polar coordinates are the polar angles $\left[\theta \left(0\right),\varphi \left(0\right)\right]$ and $\left[\theta \left(t\right),\varphi \left(t\right)\right]$, respectively. The CH bond angle with respect to the bilayer normal ${\mathbf{N}}_{\text{B}}$ is $\theta \left(0\right)$ or $\theta \left(t\right)$. However, the angle $\widetilde{\text{β}}\left(t\right)$ whose fluctuations are analyzed with the use of the spherical-harmonic addition theorem (cf. Eq. 22) is different from $\left|\theta \left(t\right)-\theta \left(0\right)\right|$ and does not depend on the director axis. (B) Alternatively, the orientation of the CH bond ${\mathbf{v}}_{\mathrm{CH}}$ is described by the Euler angles $\left(\alpha ,\beta ,\gamma \right)$. Angles $\beta$ and $\gamma$ define the orientation of ${\mathbf{v}}_{\mathrm{CH}}$ with respect to the bilayer normal ${\mathbf{N}}_{\text{B}}$ (director axis), and their fluctuations are analyzed in the new theoretical framework (Eq. 17). The schematic in (B) is adapted from (58). Note that use of the spherical-harmonic addition theorem is applicable to isotropic liquids with unrestricted motions, while the representation in terms of Euler angles includes the director axis (bilayer normal) and orientational order parameters of the lipids. Analysis of multiscale composite motions of liquid-crystalline membranes thus becomes possible with the latter approach. To see this figure in color, go online.