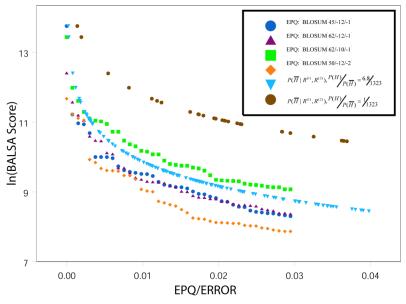
Figure 6.

The natural log of the BALSA score versus the associated EPQ given the four scoring matrix and gap penalty pairs, P(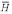│ R⁽¹⁾, R⁽²⁾) under the true probability ratio of a homolog versus not, P(H) / P(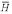) = 6.8 / 1323, and the a priori assumption P(H) / P(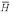) = 1 / 1323. The probability of a non-homolog given the two sequences, P(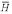│ R⁽¹⁾, R⁽²⁾), obtained from the Bayes factor under the true probability ratio is a good estimate of the EPQ independent of the parameters. P(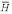│ R⁽¹⁾, R⁽²⁾) under the a priori assumption is a conservative estimate for the true EPQ and posterior probability obtained from the true prior odds ratio.