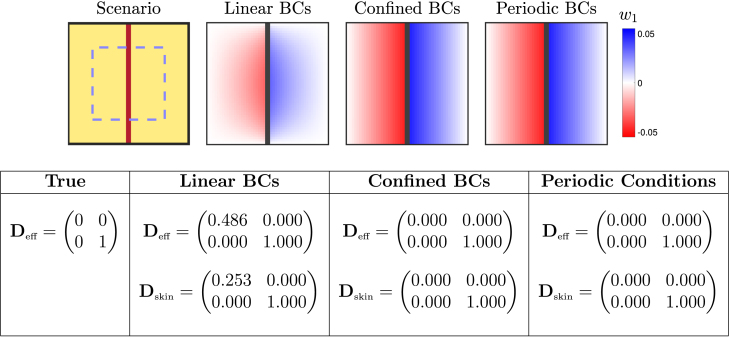
Fig. 3.

Performance of different homogenisation boundary conditions (BCs) for an averaging volume occupied by a thin strand of fibrotic obstruction. Conductive tissue is shown in yellow, and fibrotic obstruction in dark red (dark grey in visualisations of the closure problem solution). Pictured are the solutions to the closure subproblem (9) for the variable $w_1$, which when averaged together with the $w_2$ solutions (not pictured) result in the conductivity tensors given in the table. Confined and periodic conditions result in a constant gradient solution, such that $\langle \mathbf{D}({\mathbf{e}}_1+\nabla w_1)\rangle =\mathbf{0}$ and zero horizontal flow is correctly predicted. Linear boundary conditions result in a degradation of that solution near the boundaries, and this results in an effective tensor that still permits some horizontal flow. The effects of skin are considered by calculating ${\mathbf{D}}_{\mathrm{eff}}$ for only the dashed blue rectangle (but still solving the closure problem over the full domain). Use of skin to shift averaging away from the boundaries helps reduce this effect but falls far short of eliminating it.