Statistical Mechanics meets Single Cell Biology

Abstract

Single-cell omics is transforming our understanding of cell biology and disease, yet the systems-level analysis and interpretation of single-cell data faces many challenges. In this perspective, we describe the impact that fundamental concepts from statistical mechanics, notably entropy, stochastic processes and critical phenomena, are having on single-cell data analysis. We further advocate the need for more bottom-up modelling of single-cell data, and to embrace a statistical mechanics analysis paradigm to help attain a deeper understanding of single-cell systems biology.

Introduction

Statistical mechanics emerged in the 19^th century in an attempt to explain macroscopic observables of physical systems in terms of their microscopic properties ^{1, 2}. One of the first examples was Maxwell’s kinetic theory of gases, which describes macroscopic features such as gas pressure and temperature in terms of the underlying velocity distribution of gas molecules. Building upon Maxwell’s work, it was generalized and formalized by Boltzmann and Gibbs, who introduced the key notions of macrostate and microstate, which would lay the foundation for statistical mechanics to help explain a wide range of natural phenomena. From describing phase transitions between different states of matter (e.g. superconductivity) ², to predicting extinction events in ecosystems ^{3, 4}, to modelling protein-folding ^{5, 6}, the framework, concepts and tools provided by statistical mechanics have proved to be universal, profound and of great utility. In light of this universality, the ongoing single-cell revolution ^7–9 offers the unprecedented opportunity to apply these same principles to cell biology. Indeed, single-cell technologies make it possible to measure molecular properties of single cells in a genome-wide and high-throughput manner ¹⁰, thus inviting statistical mechanics to help bring about a deeper understanding of tissue function (the macrostate) in terms of single cell properties (the microstate). In effect, cell biology and statistical mechanics are finally meeting at a crossroads ^{11, 12}.

One key area of systems biology where synergy between single-cell biology and statistical mechanics has emerged is in relation to modeling Waddington epigenetic landscapes, a simple yet attractive conceptual model for describing cellular development and differentiation, first proposed over 60 years ago by embryologist Conrad Waddington ^{13, 14}. Although we now know that the original model proposed by Waddington only provides a fairly crude description of development ^15–17, three foundational ideas remain. First, cells of an organism can be distinguished in terms of their developmental potential to give rise to widely different numbers of other cell types, indicating the existence of a differentiation potency hierarchy, traditionally depicted as the elevation in the landscape, and which hints at the existence of a potential energy function. Second, cells preferentially occupy specific stable regions in the landscape, termed local attractors by Waddington, and which correspond to observed cell types. Third, the landscape is “canalized” into specific basins of attraction, defining low-energy paths that connect attractor states to each other. From a theoretical perspective, all of these landscape features have traditionally been modelled in terms of dynamical systems theory ^18–20, and indeed were directly derived from it ²¹. Although successful in recapitulating principles of differentiation via epigenetic landscape representations ^{19, 20}, the dynamical systems theory framework exhibits many intrinsic limitations, notably the inherent difficulty of solving high-dimensional equations representing realistic gene regulatory networks (GRNs) ²². Consequently, this approach to modelling Waddington landscapes has been limited to differentiation processes that can be reasonably well described by simple low-dimensional regulatory network motifs, such as the PU1-GATA1 system underlying the binary erythroid-myeloid fate decision of common myeloid progenitor cells ¹⁹, or the Gata6-Nanog antagonism that underlies the binary epiblast-primitive endoderm fate decision in early mouse development ^23–25. Modelling these landscapes for more general, complex and high-dimensional GRNs, whose complete topological structure are not yet known, thus calls for an entirely different approach, both experimentally and theoretically. This new approach is enabled by single-cell omics.

Single-cell omics is altering our understanding of cellular development and Waddington landscapes in two fundamental ways. First, it allows mapping of the dynamic evolution of functional cellular states at single-cell resolution ^{10, 16}, an experimental leap that is fundamentally redefining the Waddington landscape picture in terms of a more general and abstract representation known as a state-manifold ¹⁶. Much of this transformation has been enabled by advances in single-cell lineage-tracing technologies ^{16, 26}, which have allowed more precise mapping of single-cell dynamics. Second, single-cell omics allows genome-wide quantification of transcripts and other informative features in large cellular ensembles, and this means that novel, more powerful quantitative modelling approaches, which overcome the limitations of more traditional methods, are now possible. Indeed, in parallel to the many experimental advances, there have been equally important theoretical and computational leaps, with many of these driven or inspired by statistical mechanics.

Here we describe and highlight theoretical and computational advances that are rooted in statistical mechanics, alongside other important computational methods, providing a unified account of their roles in modelling state-manifolds. During the discussion, we make a broad distinction between bottom-up modelling approaches versus more traditional top-down based methods, discussing their advantages and limitations. We also describe how the tools described herein can help address some of the intrinsic challenges of single-cell data analysis, including the high dropout rate ²⁷ and biological noise ^{28, 29}, yet for a more detailed account of the specific computational challenges posed by single-cell data analysis and computational methods to address them, we refer the reader to recent excellent reviews elsewhere ^{30, 31}.

GRN-based modelling of Waddington landscapes

Modelling of Waddington landscapes has long been a key goal of cell biology and molecular medicine, as it embodies the need for a predictive mathematical framework in which to understand how transcription factors orchestrate cellular development and differentiation. The traditional approach to deriving potential energy functions and Waddington landscapes has been through direct modelling of the dynamic changes in transcription factor (TF) concentrations, as determined by a set of non-linear differential equations representing a GRN ¹⁸ (Fig. 1a). The underlying GRN has to be known in advance and is often derived from prior biological knowledge and experiments, providing a network representation of the activating and inhibitory regulatory interactions thought to be operating in single-cells. The Waddington landscape itself, embodied by a potential energy function, is in principle then obtained by solving the set of differential equations, yielding a statistical mechanical Boltzmann distribution that describes the probability of finding the cell in specific states (Fig. 1a) However, in practice the solution to these non-linear equations is non-trivial. This is because realistic GRNs define high-dimensional systems that exhibit a large number of stable attractor states, corresponding to observed cell types, and where the dynamics of TF concentrations cannot in general be expressed in terms of gradients of a potential energy function ³². Although theoretical solutions have been obtained that allow inference of quasi-potential functions, thus allowing visualization of Waddington landscapes and successfully capturing known bifurcation dynamics in development (Fig. 1a) ^{18, 32–36}, this approach has been limited to small GRNs consisting of a few TFs and containing only 2 to 3 attractor states ^{18, 37}. Even for relatively small GRNs, the number of unknown parameters requiring prior specification can be considerable ^{18, 37}. Moreover, the modelling derived from a GRN has been unable to predict more complex patterns of cell-fate trajectories, such as state-convergence ¹⁶, or multifurcations ³⁸, as observed for instance in the hematopoietic system. An alternative to solving the dynamic equations of a GRN has been to use a Boolean representation whereby gene expression is binarized to an on/off variable and where the dynamics is described by asynchronous update rules specified by the GRN ^{39, 40}. While these Boolean approaches have successfully recapitulated the heterogeneity of gene-expression attractor states in blood stem cells ³⁹, they still depend on prior knowledge of the GRN, which is not available for most systems. More fundamentally, it has also been challenging to explain the “arrow of time” in gene expression dynamics, that is, the spontaneous directional temporal flow of gene expression changes during development ⁴¹. As we shall see next, the ability to generate genome-wide single-cell RNA-Seq (scRNA-Seq) data for large numbers of cells ⁷ has enabled the introduction of novel modelling paradigms that address these limitations.

Figure 1 |. Statistical Mechanical modelling of state-manifolds.

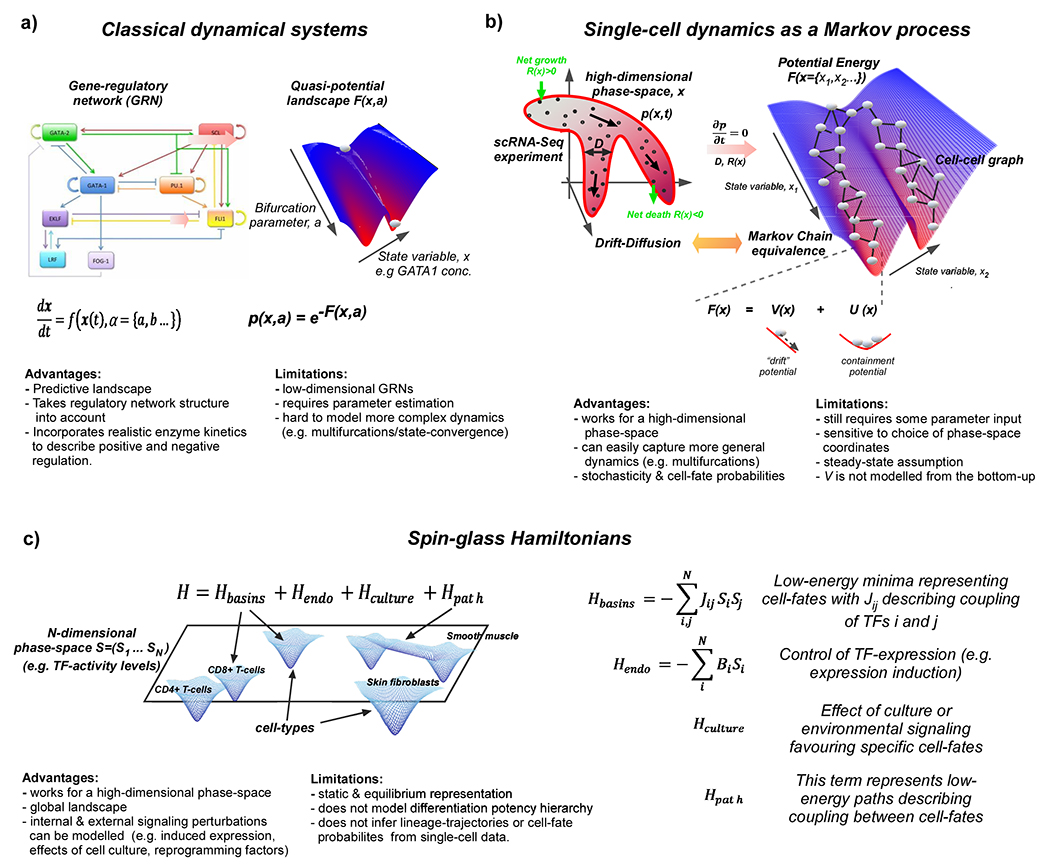
a. The traditional method to modelling Waddington landscapes has been by direct integration of the dynamics of molecular concentrations (e.g. TF-expression levels) as determined by a set of differential equations describing a gene-regulatory network. This solution is embodied by a potential or quasi-potential function F(x,a) allowing visualization of Waddington landscapes and modelling of bifurcation dynamics as a function of various system parameters (labelled as a). The probability of finding a given cell in a given state labelled by a, is then given by the statistical mechanical Boltzmann probability distribution p(x,a), as shown. b. Single-cell omics generates scRNA-Seq data for large numbers of cells, allowing for empirical probabilistic modelling of single-cell dynamics via a class of statistical mechanical PDEs known as drift-diffusion models (see Box-2). These describe the dynamic evolution of the probability cell density p(x,t) in a high-dimensional phase space encoded by x. This equation can be solved for the potential energy function F(x) under steady-state assumptions and with prior specification of parameters describing stochastic diffusion (D) and net birth-death rates R(x) (see Box-2). The solution exploits an equivalence between PDEs and random-walk operators on graphs, and entails the construction of a Markov Chain process on a nearest-neighbor cell-cell graph (as depicted) where the probabilities of the Markov Chain are determined by differentiation potency gradients (encoded by V(x) and stochastic diffusion (encoded by D). c. Spin-glasses are a class of statistical mechanical model that have been used to model systems of many interacting particles and which exhibit many equivalent low-energy attractor states. They have been applied to model a global state-manifold landscape, with each cell-type defining a low-energy attractor state and where the interactions are modelled in a high-dimensional (N large) phase space (labelled here by “spin”-vectors S_i, i=1…N) representing Boolean (i.e. on=1, off=−1) regulatory activity of N transcription factors. The Hamiltonian energy function specifying the energy landscape contains a quadratic term in S, which specifies the basins of attraction representing the different cell-types, a linear term in S which can help model the effect of endogenous perturbations (e.g. expression induction), a term reflecting external signalling (e.g. cell culture or intercellular communication effects) and a term describing low-energy paths between cell-fates. The coupling parameter J_ij represents the interaction strength, or influence, two TFs i and j have on each other in determining all cell-fate attractor states in the model, and is determined by the Boolean phase space coordinates specifying each cell-type. The state adopted by a cell is determined by minimizing the Hamiltonian energy function. If this function only contains the quadratic term, there are many equivalent low-energy minima, each one corresponding to a distinct cell-fate. The additional terms in the Hamiltonian then tilt the balance in favour of specific cell-fates, depending on whether specific TFs are induced/inactivated and external signalling factors.

State-manifold modelling from scRNA-Seq data

Single-cell dynamics as a stochastic Markov process.

Modelling of the state-manifold from scRNA-Seq data is critical for a deep understanding of cell biology and for realizing the goals of molecular and regenerative medicine. It entails the inference of three major landscape features: local attractor states representing functionally relevant cell types, their elevations in the manifold that influence their differentiation potential, and the low-energy paths, often called lineage trajectories, that connect these attractor states together. Deriving all of these landscape features has been possible through explicit modelling of single-cell dynamics as a stochastic process ^{42, 43}. There are two main reasons why a stochastic process is an appropriate description of single-cell dynamics. First, measuring the transcriptome in the same cell at different positions within the manifold is impossible, since the very act of measurement destroys the cell. Thus, in the absence of lineage tracing, inferring each cell’s past and future lineage trajectory requires a model which probabilistically assigns representative ancestors and progeny of the given cell from the large ensemble of cells measured at earlier and later timepoints (Fig. 1b). Second, molecules within cells undergo truly stochastic rather than continuous changes ^{28, 31, 44}, which means that at the most fundamental level single-cell dynamics is probabilistic. However, it is worth noting that deterministic continuous-like single-cell dynamics may nevertheless emerge from underlying probabilistic processes.

Mathematically, one describes the sampling of single cells in an experiment and the subsequent inference of their cellular states as defining an empirical probability distribution over such states, which for very large numbers of cells will converge to the true (but unknown) distribution. The definition of cellular states requires specification of an appropriate set of phase-space coordinates to use, which may involve analytical steps known as feature selection and dimensional reduction. Once specified, the dynamic evolution of the probability distribution in phase space is complex, yet biological developmental processes are relatively stable and generally do not depend on the specific series of steps that led to a given state, which allows the underlying stochastic dynamics to be viewed as a memory-less Markov process ⁴². While some recent work suggests that a Markovian assumption may not strictly hold for cellular differentiation ⁴⁵, it is nevertheless a useful simplifying approximation that allows for an elegant and general formulation of single-cell dynamics in terms of a certain class of partial differential equations (PDEs) known in the Statistical Mechanics literature as drift-diffusion or Fokker-Planck equations (Box-1) ^{42, 46}.

Box 1 |. Drift-diffusion models and Markov Chain equivalence.

Drift-diffusion PDE:

In both time course and static scRNA-Seq datasets, single cells can be viewed as part of a dynamic Markov process, in which cells leave and enter specific states in phase space according to the Chapman-Kolmogorov master equation ¹⁸⁰, from which the drift-diffusion (also known as Fokker-Planck) partial differential equation (PDE) model is derived. As applied to single-cell data, the PDE describes how the probability of finding a cell at a given point in state-space changes in time according to (i) a dynamic component called drift (which captures differentiation potency gradients), (ii) a dynamic component called diffusion (which captures stochastic fluctuations around the trajectory), and (iii) a general net birth/death process that models growing or dying cell populations, including spatial migration. The PDE model is:

$$\frac{\partial p(\mathit{x},\mathit{t})}{\partial t}=\nabla [\mathit{p}(\mathit{x},\mathit{t})\nabla \mathit{F}(\mathit{x})]+\mathit{D}{\nabla }^2\mathit{p}(\mathit{x},\mathit{t})+\mathit{R}(\mathit{x})\mathit{p}(\mathit{x},\mathit{t})$$

where p(x,t) describes the probability of finding a cell at time t at position x in phase space, F(x) describes the potential energy function at phase space coordinate x and controls the drift process, D is the diffusion coefficient and R(x) is the net birth-death rate for a cell located at position x in phase space (see Fig. 1b).

PBA (Population Balance Analysis):

PBA is the name given by Weinreb and Klein ⁴² to the algorithm that solves the above PDE under steady-state conditions $\frac{\partial p}{\partial t}=0$, and given estimates for parameters D and R(x) as input. However, PBA refers to the law of mass (probability) conservation, from which the above PDE can be equivalently derived from ^{33, 42}. The net birth-rate R(x) can be estimated from literature or from the expression of genes involved in cell-growth and cell-death (e.g. apoptosis) processes. Variants of PBA that do not require prior estimation of R(x) have recently been proposed ¹⁸¹. The solution of the PDE entails estimation of the potential energy function F(x) that quantifies the state-manifold, and which is made up of two separate potentials V(x) and U(x) so that F(x)=V(x)+U(x). The former describes the potential energy associated with differentiation potency gradients, whereas the latter describes a containment potential that counteracts diffusion to keep cells close to the low-energy paths, and which in general is approximated by $U(x)=-D\log [p(x)]$ ³³ (see Fig.1b).

Solution via Markov Chain equivalence:

The full solution of the above PDE exploits a mathematical equivalence to random-walk operators on graphs ¹⁸², so that the solution can be derived on the finite state space of a graph. The graph itself is constructed from the scRNA-Seq data, as a k-nearest-neighbour cell-cell graph, where each node is a cell and where the k neighbours of a given cell are the k most similar cells according to a suitable distance metric in phase space. From this unweighted graph, a graph Laplacian matrix is constructed, which describes properties of the random walk on this graph. The potential V(x_i) is then obtained as the matrix product V=L⁻¹R. Finally, the Markov Chain solution is obtained by the Arrhenius transition probability formula:

$$p(i\to j)\sim e^{(V(x_i)-V(x_j))/D}$$

for (i,j) a pair of cells that are connected in the graph, and which equals 0 for pairs of cells that are not neighbours. From this Markov Chain, and given a root-state, pseudotime and cell-fate probabilities can be computed ⁴².

Solving the drift-diffusion equations: inference of the state-manifold.

By drawing upon equivalence principles linking drift-diffusion equations to random-walks on a graph, Weinreb and Klein showed in a seminal method called PBA (Table 1) how, given a timecourse scRNA-Seq dataset and parameter estimates, the drift-diffusion equation can be solved under steady-state assumptions, to infer the underlying Markov process as a Markov chain on a cell-to-cell nearest-neighbor graph ⁴² (Box-1, Fig. 1b). The Markov chain itself entails inference of a potential energy function that directly quantifies the elevation and curvature of the state-manifold (Box-1, Fig.1b). One component of this potential energy directly defines the Markov Chain process on the cell-cell graph (Box-1), describing the drift of cells along differentiation potential gradients, and can therefore be used to place cells along a differentiation hierarchy (Fig.1b). From the estimated Markov chain, it is subsequently possible to infer lineage-trajectories, pseudotime ⁴⁷ and cell-fate probabilities ⁴⁸, thus subsuming a large number of previously proposed lineage-trajectory inference algorithms ⁴⁹, including popular tools such as Monocle ^{47, 50, 51} and Diffusion Maps ^{52, 53}, into one common framework ⁴². For instance, the Palantir algorithm ⁵⁴ (Table-1) also builds a Markov Chain on a cell-cell network but does so empirically without an explicit formulation in terms of a PDE. In Palantir, a cell’s potency is approximated by the Shannon entropy (Box-2) over the estimated downstream cell-fate probabilities. Another proposed method is Waddington-OT ⁴³ (Table-1), which formulates the inference of the underlying Markov chain as an optimization problem in optimal transport (OT) theory ⁵⁵. OT-theory itself can be viewed from the lens of classical dynamics as solving a least action principle whereby the temporal couplings of single cells (i.e. the Markov Chain that determines the lineage trajectories) is such so as to minimize the flow of kinetic energy between neighboring timepoints, with the mass and velocity of the kinetic energy playing the roles of cell-density and potency gradients, respectively ⁴³. Waddington-OT is an extension of this that can capture stochastic diffusion dynamics, as well as cellular birth and death rates, making it very similar to a tool like PBA. While all these tools have been widely tested on timecourse scRNA-Seq data, it is worth pointing out that they are equally applicable to pseudotime-resolved snapshot scRNA-Seq data, as elegantly demonstrated in the case of PBA ⁴⁶ and Palantir ⁵⁴.

Table 1 |.

Algorithms and software for quantifying state-manifolds from scRNA-Seq data

Name	Description	Programming language	Web links	Reference
Modelling and visualization of state-manifolds from (temporal or pseudotemporal) scRNA-Seq data
PBA	Drift-Diffusion Markov Chain equivalence	Python	https://github.com/AllonKleinLab/PBA	Weinreb et al 42
Waddington-OT	Uses Optimal-Transport	Python	https://github.com/broadinstitute/wot https://broadinstitute.github.io/wot	Schiebing er et al 43
pseudodynamics	Drift-Diffusion PDE	MatLab	https://github.com/theislab/pseudodynamics	Fischer et al 59
Velocyto	RNA-velocity	R & Python	https://velocyto.org	Le Manno et al 146
scVelo	RNA-velocity	Python	https://scvelo.org	Bergen et al 147
Palantir	Markov-Chain based	Python	https://github.com/dpeerlab/Palantir	Setty et al54
varID	Variability/cell-fate transitions	R	https://github.com/dgrun/RaceID3_StemID_2_package	Gruen et al 83
HopLand	Hopfield neural net-based modelling	MatLab	https://github.com/NetLand-NTU/HopLand	Guo et al 35
NetLand	Visualization of Waddington landscapes from GRNs	Java	http://netland-ntu.github.io/NetLand	Guo et al 165
CALISTA	Modelling and visualization tools	R & MatLab	https://www.cabselab.com/calista	Gao et al 156
Estimation of differentiation potency from scRNA-Seq data
CytoTRACE	Gene-Count based measure	R	https://cytotrace.stanford.edu	Gulati et al 121
SCENT/LandSCENT	Signalling Entropy based estimation	R	https://aeteschendorff-lab.github.io/software/LandSCENT/ https://github.com/ChenWeiyan/LandSCENT https://github.com/aet21/SCENT	Teschend orff et al 101 Chen et al 138 185
StemID/StemID 2	Transcriptome Entropy	R	https://github.com/dgrun/RaceID3_StemID_2_package	Gruen et al 103
SLICE	Gene-ontology entropy	R		Guo et al 102
scEpath	Uses a scRNA-Seq based correlation network	MatLab	https://github.com/sqjin/scEpath	Jin et al 127

Box 2 |. Entropy in Single Cell Biology.

a). Entropy definitions

There are two common definitions of entropy, one derives from Statistical Mechanics (due to Boltzmann ¹⁸³) and another derived from Information theory (due to Shannon ¹⁸⁴).

*. Statistical or Boltzmann entropy

Given a system composed of n microscopic entities (e.g. atoms, molecules, cells), where each one can be in a finite number of r states, so that n_i = number in state i and with $n=n_1+\dots +n_r$, the Boltzmann entropy is defined by the equation

$$S=k\ln W$$

where ln is the natural logarithm, k is a constant, and W is the statistical weight defined as the number of different ways to distribute the n entities among the r states, keeping each n_i fixed. For n large (n> >1), this entropy can be approximated as

$$S\approx -k{\sum }_{i=1}^r{p}_i\ln p_i$$

where $p_i=n_i/n$ is the probability of finding any of the microscopic entities in state i.

*. Information or Shannon entropy

Shannon’s entropy is defined directly in terms of the equation

$$S=-{\sum }_{i=1}^r{p}_i\ln p_i$$

where p_i defines a probability distribution for a discrete random variable taking any one of r values. As with Boltzmann’s entropy, Shannon entropy is maximized when all p_i are identical, i.e. when $p_i=1/r$. This corresponds to a state of maximum uncertainty (or least information) as to which state the variable is in.

b). Applications to single cell biology

Within the realm of single-cell omic data analyses, entropy has appeared mainly in two different contexts. One application is to the quantification of heterogeneity or similarity between cells or genes. The other application is to the quantification of differentiation potency.

1. Quantification of heterogeneity or similarity

   Given a number of cells (or genes), the similarity of their omic profiles (e.g. expression) can be quantified in terms of their mutual information, which can be expressed in terms of entropy. Specifically, if cells exhibit near identical molecular profiles, knowledge of one profile informs us a great deal about the other profiles, defining a state of high mutual information or low entropy. Conversely, given random profiles, knowledge of one informs us little about any other, which thus represents a state of low mutual information or high entropy. Thus, mutual information has been used as a distance metric between cells (or genes):

   1. Mutual information: Given a set of p random variables X_i (e.g. p gene expression profiles, or p single-cell profiles), their mutual information $I(X)=I(X_1,\dots ,X_p)$ can be expressed as

      $$I(X)={\sum }_{i=1}^{p}S(X_i)-S(X)\ge 0$$

      which is equal to zero if and only if all X_i are statistically independent. In the above, S(X) is the Shannon entropy of the multivariate distribution $X=(X_1,\dots ,X_p)$.
   2. Covariance entropy: For a continuous multivariate Gaussian distribution specified by a matrix X with covariance matrix Σ, the global heterogeneity can be quantified in terms of the covariance entropy, which can be written as ¹⁰⁴:

      $$S_X=\frac{1}{2}\log \det (\text{Σ})+constant$$

      For p well correlated genes (cells) across n cells (genes), the determinant of the covariance matrix approaches zero and the entropy is low. Entropy is maximized for p uncorrelated genes (cells).

2. Quantification of differentiation potency

   Given the transcriptomic profile of a single cell, entropy has been used to quantify the relative potency between cells:

   1. Transcriptome (StemID) entropy: This is defined by the Shannon Entropy of the transcriptomic profile of a cell. In effect, this measures the uniformity of the read count distribution across genes. This entropy definition is used in the StemID algorithm ¹⁰³ to help assign a stemness index to cell clusters, but can be applied to individual cells.
   2. SLICE entropy: This is defined by the Shannon Entropy of the Gene-Ontology (GO) activation profile of a cell. This activation profile is defined over GO-clusters (i.e. clusters of genes with similar GO-annotations), and where the activation of each GO-cluster is derived from the expression levels of the genes annotated to that cluster. In effect, this entropy quantifies the uniformity of activation levels over GO clusters. This entropy is used in the SLICE algorithm ¹⁰².
   3. Diffusion or signalling entropy: This is defined by the Entropy Rate of a signalling (diffusion) process in a cell. This definition entails the use of an interaction network (e.g. a PPI network), which is integrated with the transcriptomic profile of the cell, to define a stochastic matrix P with entries p_ij. This cell-specific stochastic matrix describes a Markov chain diffusion process, and the Entropy Rate (SR) can be thought of as quantifying the efficiency of the diffusion process to “explore” the whole network. This entropy rate is used in the SCENT/LandSCENT algorithms ^{101, 138} and is formally defined by

      $$SR=-{\sum }_{i,j}{\pi }_i{p}_{ij}\log p_{ij}$$

      where π is the steady-state probability distribution over the network, i.e. it is invariant under a transformation of the stochastic matrix: $\pi P=\pi$.

Beyond its clear theoretical importance, methods like PBA or Waddington-OT have enabled critical novel insight into cellular development, fundamentally altering Waddington’s traditional picture of continuously diverging cell-fate transitions. For instance, in the case of myelopoiesis, PBA predicted coupling of dendritic and monocyte progenitors, and separately also of monocyte and granulocyte progenitors, but no granulocyte-dendritic coupling, suggesting two alternative paths for differentiation into monocytes ⁴⁶. Such “state-convergence” has been confirmed experimentally ⁵⁶, and has been observed very widely throughout cellular development via lineage-tracing studies ^{57, 58}. Building upon the drift-diffusion model of PBA, a more recent tool called pseudodynamics ⁵⁹ (Table 1), that integrates scRNA-Seq data with measured or inferred cell population sizes, has also led to important new insights. Importantly, pseudodynamics can improve the estimation of cellular birth and death rates, dynamic processes that can otherwise confound cellular flux gradients associated with differentiation. As a concrete example, pseudodynamics was applied to scRNA-Seq data describing T-cell maturation, naturally revealing two phases in Waddington’s landscape: a low-drift, high-diffusion T-cell receptor (TCR) beta selection phase, followed by a high-growth and high-drift phase, associated with a large increase in T-cells expressing both TCR-alpha and beta ⁵⁹.

Modelling cell types as local attractors.

It is worth noting that the inference of the state-manifold using tools such as PBA or Waddington-OT does not provide a definition of cell-type. The identification and modelling of cell types from scRNA-Seq data is however a critically important endeavour ^60–62, especially for the ongoing Human Cell Atlas efforts that aim to categorize the full repertoire of human cell types ^{9, 10, 63}. From a mathematical standpoint, modelling cell types in terms of stable local attractors in phase space is sensible given that cell types are observed to be relatively stable entities. The local attractors can be visualized as multi-dimensional basins that specify a position (or region) in phase space where the cell-type is defined, as well as a local curvature that reflects cell-type stability.

Traditionally, the attractors representing cell types have been defined as high-density clusters of cells, derived by applying a series of analytical steps to single-cell omic data, which generally may include feature selection, a linear or non-linear dimensional reduction that embeds and visualizes the data in a low-dimensional space , and a choice of clustering algorithm ^64–66. For instance, a set of popular clustering algorithms are those based on community detection on cell-cell graphs ^67–71, as constructed with tools like PBA, Diffusion Maps or Palantir. A key challenge in defining cell-types is the choice of phase-space coordinates. In addition, each of the steps above often involves a fairly arbitrary choice of parameter values, which depending on the value taken may lead to widely different clusters ⁷², and hence to plausibly different definitions of cell-type. Thus, more principled ways to define cell types are needed. For instance, selecting the most variable genes is a popular procedure, yet not all highly variable genes may be relevant to the biological cellular processes that define a cell-type. A more sensible choice of coordinates may be to focus on transcription factors (TFs) as these proteins orchestrate cellular development and are fundamental to reprogramming and lineage-conversion experiments ^73–75. Their regulatory activity should therefore be more informative and perhaps even sufficient to define the functionally relevant repertoire of cell types. However, estimating regulatory activity from single-cell omic data is challenging. In the case of single-cell assay for transposase-accessible chromatin sequencing (scATAC-Seq) data, DNA accessibility of TF-binding motifs, although highly informative, does not equal regulatory activity ⁷⁶. In the case of scRNA-Seq data, using TF-expression levels as a proxy for regulatory activity has been successfully applied in the hematopoietic system ⁷⁷, but is generally a problematic procedure due to their typically low noisy expression and high dropout rate ²⁶. An alternative strategy, illustrated by a method called SCENIC ⁷⁸, infers regulatory activity by applying a reverse-engineering algorithm ^79–81 to infer TF-regulons ⁸² from the scRNA-Seq data, yet the sensitivity of this procedure is unclear given that the inference is still anchored on TF-expression levels ^{26, 83, 84}. Another alternative approach is to infer regulatory activity from the expression levels of TF-target genes (i.e. both direct binding and downstream indirect targets), as derived from bulk studies (e.g. ChIP-Seq ⁸⁵ or multi-tissue bulk RNA-Seq datasets such as from the Genotype–Tissue Expression (GTEx) project ⁸⁶), or from TF-binding motif databases ^{87, 88}. This strategy circumvents the direct use of TF-expression levels, and because it uses a larger pool of TF-targets, it can also tolerate relatively high dropout rates ^{89, 90}.

In addition to the position of the attractors, their curvature may also convey important biological information: for instance, multi-or-bipotent progenitor cells undergoing fate decisions generally exhibit higher levels of intercellular heterogeneity ^91–93, reflecting a higher propensity to diffuse more widely around their attractor states, implying a relatively flat or low-curvature basin. In this regard, it is worth noting that methods like PBA ⁴² and Waddington-OT ⁴³ exploit the typically large number of measured cells to empirically model the curvature of attractor basins. Indeed, in PBA, the potential energy function has a second component representing a ‘containment potential’ that directly describes the curvature of the basin, and which is estimated from the gradients in observed cell-density in phase space, assuming the degree of diffusion is also known (Fig. 1b). However, at present it is still unclear if the curvature of these basins truly reflect cell-type stability, as the underlying interpretation of such curvature is often confounded with other parameter estimation tasks such as the identification of separate cell types ⁹⁴.

Assuming regulatory activity of TFs can be reliably estimated and that cell types can be unambiguously assigned to well-defined clusters within this regulatory activity phase space, their attractor states can in principle then be modelled in a global phase space using a set of statistical mechanical models known as infinite-range spin-glasses ^{95, 96} (Fig. 1c). These models are defined by an energy function called a Hamiltonian and in general describe systems of interacting particles that display a large number of stable low-energy states, which in this specific context would correspond to observed cell types. In the spin-glass model, cell types can be represented as defining_high-dimensional ‘spin’ vectors encoding e.g. Boolean (on/off) TF-activity levels, and with strongly interacting or coupled TFs exhibiting similar activation profiles over cell-fates. An appealing feature of the spin-glass model is that it naturally allows for modelling the effects of endogenous and exogenous perturbations (e.g. environmental signaling by a differentiation factor), which breaks the symmetry of the low-energy states, favouring specific cell-fates over others. In such models, expression or signaling induction can be quantified and interpreted as order parameters that control transitions between cell-fates. The ability of a spin-glass to model a large number of different cell types within the same global manifold is important, as this could help predict the outcome of reprogramming experiments, or the presence of unintended cell-fates in specific reprogramming or organoid differentiation experiments ⁹⁷. For instance, a spin-glass was developed to model a global epigenetic landscape for over 60 cell types and 1000 TFs, and shown to be able to describe known differentiation and reprogramming dynamics ⁹⁸. However, these models are still crude and don’t incorporate essential features of the state manifold such as differentiation potency or the stability (curvature) of attractors ⁹⁸. Thus, future work would require generalization of these spin-glass models to incorporate these additional features, which could be important for improving their predictive ability. Alternatively, it has been possible to infer regulatory network relations between attractor states by binarizing TF-expression levels in scRNA-Seq data and subsequently inferring regulatory effects of TFs on each other by studying the specific transitions between cells in each attractor state ⁷⁷. Such Boolean representations of phase-space have allowed reconstruction of regulatory networks of moderate size (20-30 TFs) and with predictive potential, as shown for Hox and Sox TFs in mesoderm development ⁷⁷. However, it remains to be seen if such reverse-engineering approaches can be successfully applied to larger regulatory networks and to other developmental systems.

Bottom-up modelling of differentiation potency

Bottom-up versus top-down modelling.

So far, we have described methods that can infer relative potency gradients, cell types, branch points and lineage trajectories, which together allow visualization of the state-manifold. However, an inherent drawback of these methods is the need to impose directionality by hand, i.e. the intrinsic temporal directionality underlying differentiation processes is not automatically inferred. Although this is not a major limitation in timecourse scRNA-Seq studies, it can be a problem in static scRNA-Seq studies or in tissues where differentiation hierarchies are not well established.

To overcome this particular challenge requires an entirely different modelling paradigm, which we shall refer to as ‘bottom-up’ (Fig.2). This contrasts with the ‘top-down’ strategies discussed earlier. The distinction between bottom-up and top-down modelling arises because of the two biological length scales at which we could choose to model differentiation potency in single cells. In the bottom-up approach, differentiation potency of a cell is estimated from knowledge of its underlying molecular network state, using only measurements taken within that cell. Underlying this paradigm is the reasonable assumption that there exists a potential function, which, given some input (e.g. a cell’s RNA-Seq expression and/or chromatin accessibility profile), outputs an approximate value for the cell’s differentiation potency (Fig. 2). Such bottom-up approaches can also be described as being truly model-based, since they require explicit modelling of the potential function. Such modelling can derive from prior biological knowledge and may not require any feature selection or training, which can help avoid overfitting ⁹⁹ and has other advantages (Fig.2). By contrast, the top-down paradigm considered earlier and exemplified by methods such as PBA, Palantir or Waddington-OT, begins by analyzing all the cells in the given experiment together, to subsequently infer differentiation potency of each cell (Fig.2). Such a top-down approach generally requires feature selection or training, and a dimensional reduction step, all procedures that by definition borrow information from most, if not all, cells in the experiment. Thus, in a top-down approach the potency estimate of a given cell is not just a function of the cell’s transcriptome, but is also dependent on that of other cells. While this can help denoise single-cell potency estimates, it may also be more susceptible to overfitting as it involves many ambiguous parameter choices (Fig.2).

Figure 2|. Paradigms for estimating differentiation potency of single cells.

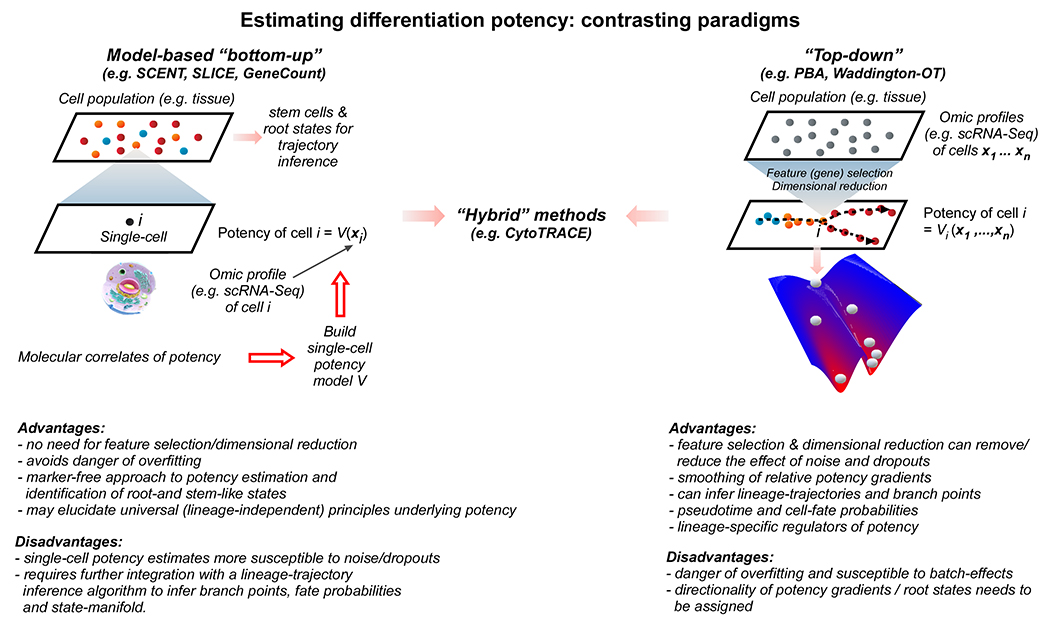
Bottom-up vs top-down paradigms for estimating differentiation potency of single cells, their advantages and disadvantages. Briefly, the bottom-up paradigm involves estimating the potency of each cell using only information measured in that cell, whilst the top-down approach analyses the collective set of cells together to infer each cell’s position in the differentiation hierarchy. The bottom-up approach is more in line with the intuition that a cell’s potency is fully determined by its molecular network state, yet the inference is more susceptible to noise. As an analogy, the bottom-up approach corresponds to using a “ruler” (e.g. SCENT) to measure the “height” (potency) of an “object” (cell) which thus only requires an act of measurement on that object. In the top-down modelling approach no ruler is available, and height needs to be inferred by comparison to other objects of known height, or alternatively only a relative height is inferred.

Bottom-up modelling of differentiation potency using molecular entropy.

A range of bottom-up methods for estimating differentiation potency of single cells have emerged ^100–103, many of which rely or are related to the notion of entropy. Entropy is a fundamental concept of statistical mechanics and information theory (Box-2), that has been widely applied in computational biology to quantify not only relative differentiation potency (Box-2), but also various types of biological heterogeneity including inter-cellular ^104–106 and epigenetic heterogeneity ^107–109. Its relevance for modeling relative differentiation potency is best appreciated by considering known biological correlates of differentiation potential (Fig.3a). One of these is the distribution of expression levels of lineage-specifying TFs, with pluripotency associated with all lineage-specifying TFs being expressed at a similar low ‘basal’ level, thus defining a state of high entropy ^110–112. From a signaling random-walk perspective, pluripotency thus reflects a high level of choice or uncertainty (i.e. entropy) as to which lineage-trajectory a random-walker would choose to move along ¹⁰⁰ (Fig.3b). In a well-differentiated cell, most of these lineage-specifying TFs are switched off except for the relatively few that define the cell-type and which are highly expressed, defining a state of low entropy. Another correlate of potency is the openness of chromatin (Fig.3a) ^{113, 114}, with an open architecture allowing more frequent protein-protein and protein-DNA interactions, reflecting the need of high-potency cells to express a larger number of TFs and downstream targets ¹¹⁵, albeit all at a low basal level. Thus, basal expression, chromatin loosening and stemness are all intimately connected ¹¹⁵, and together suggest that signaling entropy, if quantifiable, could be a useful measure of differentiation potency (Fig. 3b).

Figure 3 |. Single cell potency and molecular entropy.

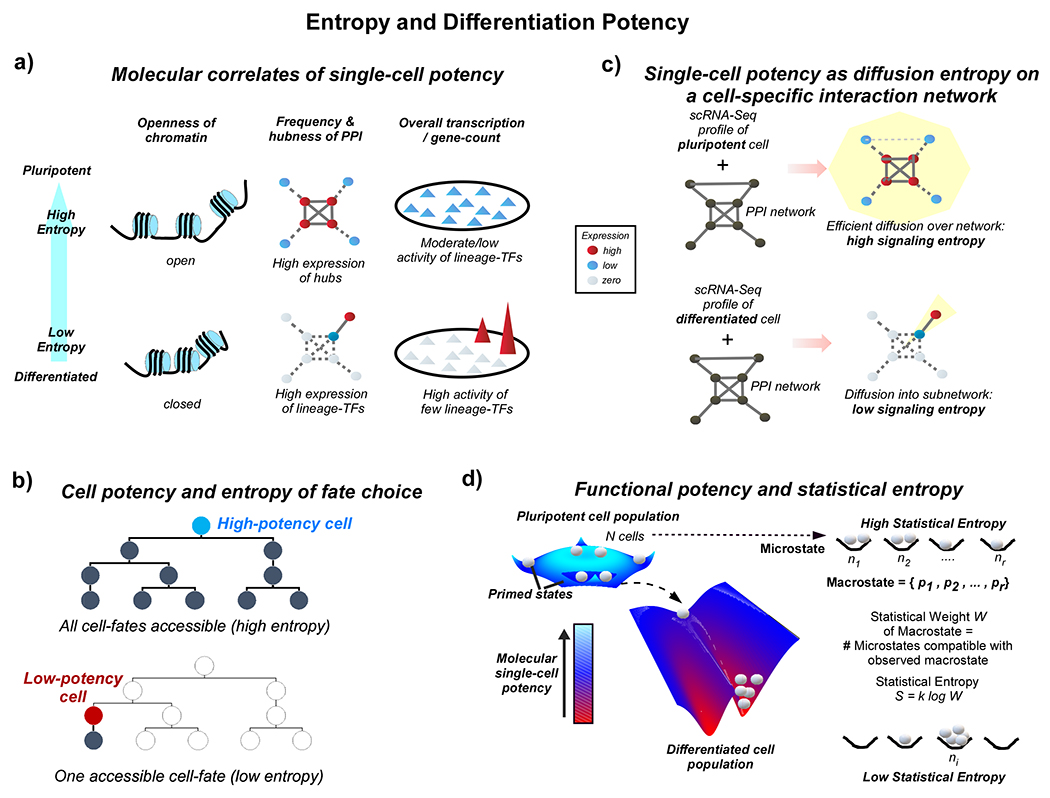
a. Examples of molecular correlates of potency, including the openness of chromatin, frequency and hubness of protein-protein interactions (PPIs) and overall number of expressed genes (gene count). A more open chromatin facilitates more PPIs and on average highly expressed proteins define hubs. A more open chromatin is also associated with a higher number of lineage-specific transcription factors (TFs) and downstream targets being all expressed at a similar low basal level. Here, the expression level of the TFs and their gene-targets is less important than the numbers of TFs being expressed, as only the latter determines the ability to quickly and fully turn on TFs and their downstream targets in response to external stimuli. Thus, stemness correlates with molecular entropy. Top panels depict the case of a pluripotent cell (high entropy), lower panels depict the case of a differentiated cell (low entropy). b. Depiction of cell potency as signalling entropy in a developmental tree, reflecting the uncertainty or choice in accessible cell-fates. c. A more detailed interpretation of cellular potency as a diffusion or signalling entropy in a PPI network. A scRNA-Seq profile of a cell is overlayed onto a high-quality cell-type independent unweighted PPI network, resulting in a weighted “signaling” network, where edge weights reflect the average expression of its nodes and therefore interaction probabilities. Solid lines represent high interaction probability, dashed thick lines intermediate probability, dashed thin lines weak probability and no edges indicate zero probability. This weighted network defines a cell-type specific stochastic matrix and Markov Chain. In the case of a pluripotent cell (top panel), where networks hubs exhibit high expression and lineage-specific TFs (non-hubs) are only moderately expressed, the signalling or diffusion entropy which measures the efficiency of the diffusion over the network is high. In the case of a differentiated cell (lower panel), most pluripotency hubs and lineage-specific TFs are not expressed, except for a few lineage-specific TFs (only one is shown for convenience) that are highly expressed. Signalling/diffusion entropy is low, because a non-central part of the network is highly activated drawing and locking in signalling flux into that subnetwork. Mathematically, signalling/diffusion entropy is calculated as the signalling entropy rate of the stochastic matrix/Markov Chain (see Box-1b for the mathematical formula). d. Quantification of functional potency in terms of Statistical Boltzmann entropy S. Depicted are two cell populations, a pluripotent one where cells are distributed fairly equally between a true pluripotent state and primed states associated with e.g. multi-lineage priming, as observed experimentally. This defines a state of high Boltzmann entropy, as there are many ways to distribute cells (each cell has its own identity) among potency states whilst preserving the global probability distribution. This probability distribution can be viewed as a microstate and as the defining feature of functional pluripotency. For a differentiated cell population, most of the cells are found in the same low potency state, except for a smaller number of progenitor cells, defining a state of low Boltzmann entropy.

One method to draw on these principles is SCENT (Table 1) ¹⁰¹. SCENT estimates differentiation potency by first integrating the genome-wide expression profile of a given cell with a protein-protein interaction (PPI) network ^{116, 117}, invoking the mass action principle to quantify the likelihood of PPIs in a cell-specific manner, and subsequently approximating potency as the signaling entropy rate (Box-2) of a random walk on the cell-specific network (Fig. 3c) ^{100, 101}. Importantly, the association between entropy rate and a cell’s potency is strongly dependent on the hierarchical and approximately scale-free nature of PPI networks ^118–120, as these networks contain signaling hubs, which tend to be overexpressed in the more potent cells (Fig.3c) ¹¹⁸. Other differentiation potency models are based on the notion of transcriptional entropy and include methods such as StemID ¹⁰³ and SLICE ¹⁰² (Box-2, Table 1). In the case of SLICE, genes with similar GO annotations are placed in GO-clusters, and a Shannon entropy is estimated over the GO-cluster activation profile (Box-2). Another important potency model is the number of expressed genes or gene-count ¹²¹ (Fig.3a), which is closely related to transcriptomic entropy and which has been shown to correlate with the degree of chromatin loosening ¹²¹. A recent comparison between SCENT, SLICE and StemID concluded that SCENT was more robust, driven by the noted correlation between potency and hub overexpression ^{101, 122}.

This comparative study also revealed that specific network hubs encoding ribosomal components are robust markers of differentiation potency, an association also seen in bulk expression data, and which is independent of cell proliferation ^{101, 122}. These observations have strong support from scRNA-Seq studies in other lineages and species including mouse and zebrafish ^{123, 124}, and suggest that the average expression level of ribosomal genes in a cell may be a universal, i.e. lineage-independent, measure of potency, reflecting a cell’s need to express a given number of lineage-specific transcription factors and downstream targets. Thus, while the utility of PPI networks has been widely debated in computational biology generally ¹²⁵, the specific application to potency estimation reveals that particular robust network features can be useful and provide unique biological insight ¹²⁵.

Hybrid top-down/bottom-up methods to potency estimation.

Another set of methods borrow elements of a bottom-up approach but require data from other cells to estimate potency of any given cell, which we therefore refer to as hybrid methods. One of these, developed by Gulati et al, is called CytoTRACE ¹²¹ (Table-1). This method is based on the gene-count measure, but given the noise in scRNA-Seq data, Gulati et al aimed to increase robustness by modifying it in two ways. First, a gene selection step is included to identify genes for which expression correlates with the gene-count per cell, as computed over all cells in the experiment. A geometric average expression of these genes is then smoothed using corresponding estimates of transcriptionally similar cells. The resulting measure, termed CytoTRACE, exhibits improved robustness over measures such as SCENT, StemID and SLICE, owing in part to the fact that CytoTRACE exploits the intercellular variation across differentiation stages in the experiment, to smooth potency estimates accordingly. Although this smoothing-step can help remove biological noise, it could in principle also have the undesirable consequence of diluting out biologically relevant heterogeneity, as with primed states in a stem-cell population ^{11, 15, 126}. In CytoTRACE, gene-selection is study-specific, which can help identify lineage-specific regulators of potency ¹²¹. By performing a meta-analysis over 40 scRNA-Seq studies, the gene-count signature on which Cytotrace is based was found to be strongly enriched for ribosomal components ¹²¹, consistent with SCENT, and thus demonstrating that universal lineage-independent features of potency can also be identified by averaging over many studies. Another hybrid method is scEnergy/scPath ¹²⁷, which is conceptually similar to SCENT, but which instead of utilizing a PPI network, tries to infer a co-expression network from the scRNA-Seq data itself, a procedure which requires information from all cells in the experiment. While reverse-engineering networks from data has been a fruitful endeavour ^{82, 128}, inferring such correlation networks from scRNA-Seq data can be problematic due to covariation patterns being naturally more susceptible to the high dropout rate and noise ^{30, 84, 89}. Thus, further investigation is needed to assess the relevance of such correlation networks for the specific task of potency estimation.

Identification of root and stem-like states in scRNA-Seq data.

An important application of bottom-up modelling is to the problem of identifying root states in scRNA-Seq data.. Root-states often represent stem-or-multipotent progenitor like cells, and their identification is critical for correctly inferring pseudotime and cell-fate probabilities ⁵⁴, for understanding differentiation hierarchies within a tissue ^129–132, and ultimately for regenerative medicine purposes ^{133, 134}. Although in differentiation timecourse studies ^{135 97}, potency gradients are generally well correlated with the timepoint itself, and therefore root-state identification presents less of a problem, the often ambiguous choice of root-state can greatly influence lineage-trajectory inference estimation ⁵⁴. In static scRNA-Seq studies, where all cells are profiled at the same timepoint ^{9, 10, 136}, root-state identification poses a much harder problem. Here, the traditional approach has been to rely on the expression levels of known stemness or progenitor markers, yet these markers are often imperfect or controversial ¹¹⁰. Compounding this, the high-dropout rate of scRNA-Seq data ^{27, 137} can often preclude the use of specific markers ^{130, 138}. Traditional stemness markers may also not be sufficiently accurate or may not even exist ¹¹⁰. Thus, there is a need for marker-free strategies that can unambiguously identify root-states, even in the background of high noise and dropout rates.

Entropy-based bottom-up methods described earlier allow in principle such stem-like root states to be identified, and can be directly integrated with existing lineage trajectory inference algorithms ^{49, 51, 121, 139}. For example, SCENT was applied to thousands of scRNA-Seq profiles from the human mammary epithelium, and subsequently integrated with diffusion maps ^{52, 139} to unambiguously identify a root state which exhibited all the hallmarks of stem and bipotent-like mammary cells ¹³⁸, a cell-state not identifiable using a traditional marker expression approach ¹³⁰. Similarly, CytoTRACE was integrated with Monocle-2 ⁵¹ to help identify the correct root state in early hematopoiesis, out of an initially large and ambiguous pool of 23 root candidates ¹²¹. Differentiation potency models have also shown value in delineating differentiation hierarchies and identifying stem-like cells in the context of diseases such as cancer, as shown in the context of Langerhans cell neoplasms ¹⁴⁰ and prostate cancer ^{101, 141}. CytoTRACE was also applied to FACS-sorted luminal cell populations from breast cancer patients, validating a luminal progenitor population of higher potency and identifying GULP1 as a novel gene driving tumorigenesis ¹²¹. In an application to hematological cancer, StemID ¹⁰³ was used to confirm depletion of leukemia stem cells in Kat2a KO acute myeloid leukemias ¹⁴².

Statistical entropy of cellular ensembles, multi-lineage priming and functional potency.

Single cell (i.e. bottom-up) potency measures also allow quantification of the heterogeneity in differentiation potency within cellular ensembles, and can thus help with the identification of primed states, such as those associated with multi-lineage priming in pluripotent and multipotent cell populations ^{15, 26, 38}. For instance, SCENT was applied to a pluripotent cell population, revealing cells of marginally lower potency that expressed higher levels of neural stem cell markers, suggesting priming into the neural lineage ¹⁰¹. More generally, heterogeneity of functional states in a pluripotent cell population has been proposed as the defining feature of functional pluripotency ¹¹, and therefore, single-cell potency measures could help quantify this level of functional potency in a general cell population. Bottom-up potency measures could also be used to quantify the multi-fork and continuous-like differentiation dynamics, as recently observed in hematopoiesis ³⁸ and that have utilized groundbreaking lineage-tracing based cell-fate mapping technologies ²⁶. From a statistical mechanical perspective, functional potency could thus be viewed as a macrostate encoded by a probability distribution over functional cellular states in phase space, and quantifiable using Boltzmann entropy (Box-2, Fig.3d). This provides a fresh theoretical perspective on the long-standing phenomenon of regulated stochasticity, whereby an individual pluripotent or multipotent cell exhibits the ability to dynamically explore phase space in a seemingly stochastic manner, yet allowing subsequent cell-divisions to predictively reconstitute the full expression heterogeneity of a pluripotent/multipotent population ^143–145. As a result of this regulated stochasticity, cells will transit between specific meta-stable attractor states associated with multi-lineage priming (Fig.3d), but in doing so will also transiently explore a wider range of states, driven by an open chromatin architecture that permits random variation in expression ^{15, 38}. Thus, single-cell potency measures provide a link between a cell’s regulatory network state, which endows the cell with the ability to transiently explore these meta-stable states, and the regulated heterogeneity of primed states in the cell population.

Bottom-up modelling using RNA velocity.

A limitation of bottom-up based approaches is that these methods require further integration with top-down algorithms to infer other features of the state-manifold such as branch points and lineage trajectories. One exception to this however, is a bottom-up approach based on the concept of RNA-velocity ¹⁴⁶ (Table-1). While not statistical mechanical in origin, RNA-velocity is based on a dynamic model of transcription, formulated for each gene in a cell, that takes the transcription, splicing and degradation rates into account. RNA-velocity hinges on the observation that for genes being transcriptionally upregulated, their mRNAs will be skewed towards nascent, unspliced transcripts, whereas for downregulated genes the skew is towards mature, spliced transcripts. By comparing the ratio of unspliced to spliced transcripts to the ratio expected under steady-state assumptions, RNA-velocity can infer the direction of transcriptional change of each gene in a given cell. Although RNA-velocity conforms to a bottom-up modelling paradigm, it is worth noting that the parameter estimation task in RNA-velocity does rely on a fraction of cells being in a steady-state condition. A generalization of RNA-velocity called scVelo, which does not require such steady-state assumptions, and which solves the kinetic models for each cell separately has recently been proposed ¹⁴⁷. The end result of these methods is assignment of a velocity vector to each individual cell, which can be graphically represented as a velocity field. This field quantifies the direction in phase space in which each cell is moving, and allows potency gradient flows, lineage trajectories and bifurcation dynamics to be inferred ¹⁴⁶. For RNA-velocity to be useful, the sampling of cells in time must be on a temporal scale matched to the half-life of mRNA, which can range from hours to days. Another caveat is that RNA-velocity may capture other dynamics not associated with potency gradients, such as for example variation associated with the cell-cycle, thus requiring additional processing to extract components relevant to modeling lineage trajectories. As with the entropy-based methods, RNA-velocity has also led to important biological insights in cancer. For instance, in glioblastoma, RNA velocity was used to show that mesenchymal and proneural glioma stem cells are just extremes in a one-dimensional continuum of hybrid mesenchymal-neural stem-cell states ¹⁴⁸.

Statistical mechanics of cell-fate transitions

So far, we have seen how statistical mechanical concepts have enabled improved modelling of state-manifolds from single-cell data. As we shall next, they also offer a powerful bottom-up perspective for modelling cell-fate transitions on these manifolds, which can help provide novel insight on the molecular mechanisms underlying these transitions ¹⁴⁹. In this regard, it is worth noting again that in Waddington’s original landscape, cell-fate transition dynamics has traditionally been modelled in terms of specific GRNs ¹⁸, which is appealing because a GRN models relevant molecular interactions within the cell, in line with a bottom-up modelling paradigm. However, as also mentioned earlier, differential equation-based modelling is limited to small GRNs, and therefore difficult to generalize to the higher-dimensional phase space of realistic GRNs. Top-down modelling approaches such as PBA ⁴² and Waddington-OT ⁴³ can overcome this limitation, but conversely do not model the regulatory interactions within individual cells and may only provide limited mechanistic insight. Taking a statistical mechanical perspective and viewing cell-fate transitions as a form of critical phase transition (Box-3), provides a much-needed bottom-up approach to modelling these transitions, effectively extending the GRN-based approach to a higher dimensional phase space.

Box 3 |. Cell-fate transitions as critical phenomena.

Critical phase transitions, critical points and universality

A large class of phase transitions are “critical” in the sense that there exists a critical point at which the phase transition behaviour of the system is “universal”, meaning that macroscopic properties of the system are determined mainly by long-range microscopic interactions, largely transcending the details of the short-range interactions that usually define the system. That is, at and near the critical point, properties of the system only depend on the global pattern of microscopic interactions, and are not dependent on the details of the microscopic elements themselves, which means that widely different systems can exhibit similar phase transition behaviour.

Correlation length power law

Denoting by t_c the critical parameter, and by t* the critical transition point, for a large class of phenomena undergoing critical phase transitions, a correlation length observable $\xi (t)$ with $t=|(t_c-t^{\ast })/t^{\ast }|$ can be shown to increase as $t_c\to t^{\ast }$ (i.e. as t → 0) according to a power law

$$\xi (t)\sim |t{|}^{-v}$$

where v is the critical exponent (a positive number). For an infinite system this means that the correlation diverges at the critical point itself, but for real-world systems that are finite in size, the correlation remains finite and is maximized at the critical point.

Pitchfork and Saddle-Node Bifurcations

Many cell-fate transitions are characterized by an abrupt change in accessible local attractors within phase space and are often described by a class of bifurcation known as subcritical pitchfork bifurcation ^{18, 20}. In this type of bifurcation, and in response to some extracellular signal, a stable multipotent attractor state gradually becomes destabilized by the emergence of additional meta-stable states representing cells primed to differentiate into specific downstream lineages. At the bifurcation or critical point, the original multipotent attractor state effectively disappears giving rise to two or more strongly stable attractor states representing the different cell-fates. A saddle-node bifurcation is another type of dynamical bifurcation associated with the emergence of an unstable “saddle-node” state in phase space, often termed a tipping point, and which has been used to describe cell-induction processes ¹⁸. Beyond the tipping point, dynamics is no longer reversible. For both types of bifurcations, the approach to criticality is characterized by increased variance and covariance in expression between genes that are relevant for the specification of the downstream fate(s).

Dynamic Network Biomarker (DNB) formalism

This is a heuristic formalism derived from dynamical systems theory as applied to a high-dimensional and general gene regulatory network, that allows construction of gene modules G from relevant omic gene expression data, and which can be used to study critical behaviour ¹⁵⁵. Gene modules are constructed using feature selection and clustering algorithms to infer gene-clusters at each timepoint and over all timepoints in a typical temporal gene expression study. A gene module exhibiting hallmarks of a cell-fate transition, i.e. increased covariation, is called a DNB and can be identified using a criticality index (see below) ¹⁵⁵. DNBs may contain key regulatory factors controlling cell-fate and/or be strongly enriched for direct and indirect targets of these regulatory factors.

Criticality indices

In the context of cell-fate transitions, a number of different criticality indices (CI) that capture the qualitative increase in covariation have been proposed ^{92, 93, 155}. In all cases, the CI is defined for a particular subset G of genes, and for a particular timepoint t. One strategy ¹⁵⁵ defines CI(G,t) as

$$CI(G,t)={\langle SD\rangle }_{G,t}{\langle PCC\rangle }_{G,t}/{\langle PCC\rangle }_{o,t}$$

where SD and PCC are the standard deviation and absolute Pearson Correlation Coefficients, and where 〈 〉_G,t indicates the average taken over genes or pairs of genes in the subset G using cells collected at timepoint t. In the above, 〈 〉_o,t means the average taken over pairs of genes with one gene in subset G and the other belonging to any other gene not in G. Recognizing that cells exhibit lower correlations as the critical point is reached, an alternative index has been proposed ⁹² as

$$CI(G,t)={\langle PCC\rangle }_{G,t}/{\langle PCC\rangle }_{\mathit{Cells,t}}$$

where the denominator now involves the average of absolute Pearson Correlations between pairs of cells at timepoint t. In essence, the CI tracks two contrasting dynamic patterns of expression covariation as the bifurcation point is approached: on the one hand, an increased covariation in gene-space, reflecting the increased variance and correlation between genes specifying the same lineage, and on the other, a reduced covariation between cells (i.e. increased intercellular heterogeneity), reflecting e.g. multi-lineage priming (see Fig.4a).

Cell-fate transition as a critical phase transition.

A large class of phase transitions in nature are ‘critical’ in the sense that there exists a critical point at which the properties of the system change abruptly in a manner that is only dependent on the global pattern of microscopic (e.g. molecular) interactions (Box-3). Two profound principles underlying critical phase transitions make them highly relevant to describing cellular differentiation. First, systems undergoing critical phase transitions do so because of underlying abrupt changes in their microscopic interaction patterns ¹⁵⁰. Cellular differentiation, which is characterized by a drastic rewiring of active regulatory interactions is a clear example ^{151, 152}. Second, specific macroscopic observables from widely different systems may exhibit the same functional behavior as the critical points defining the phase transitions are approached ^{3, 153, 154}, a phenomenon broadly referred to as universality (Box-3). One of these macroscopic observables is the correlation length, which exhibits a universal power-law behavior, in theory diverging or becoming maximal at the critical point itself (Box-3). Thus, by measuring this correlation length in cellular systems as a function of relevant system parameters, one can in principle identify the critical points at which cells undergo fate-transitions. Chen and colleagues ¹⁵⁵ showed how to construct these correlation length observables from empirical high-dimensional omic data and for cellular systems that undergo the type of dynamic bifurcations (e.g. pitchfork bifurcations ^{18, 20}) that are normally associated with cell-fate transitions (Box-3, Fig.4a). Underlying their construction is the inference of a dynamic network biomarker (DNB), reflecting interaction patterns of specific genes within the complex high-dimensional GRN, and whose covariation increases as the bifurcation or critical point is reached (Fig.4a, Box-3). Furthermore, a criticality index that captures the increased covariation near the critical point can be constructed to allow detection of the impending phase transition (Fig.4a, Box-3). By studying dynamic covariation patterns as opposed to only dynamic changes in TF expression, the DNB formalism can help overcome inherent challenges of single-cell data such as the high dropout rate and low sampling sparsity near branching events ⁸³.

Figure 4 |. Critical phenomena in development and disease.

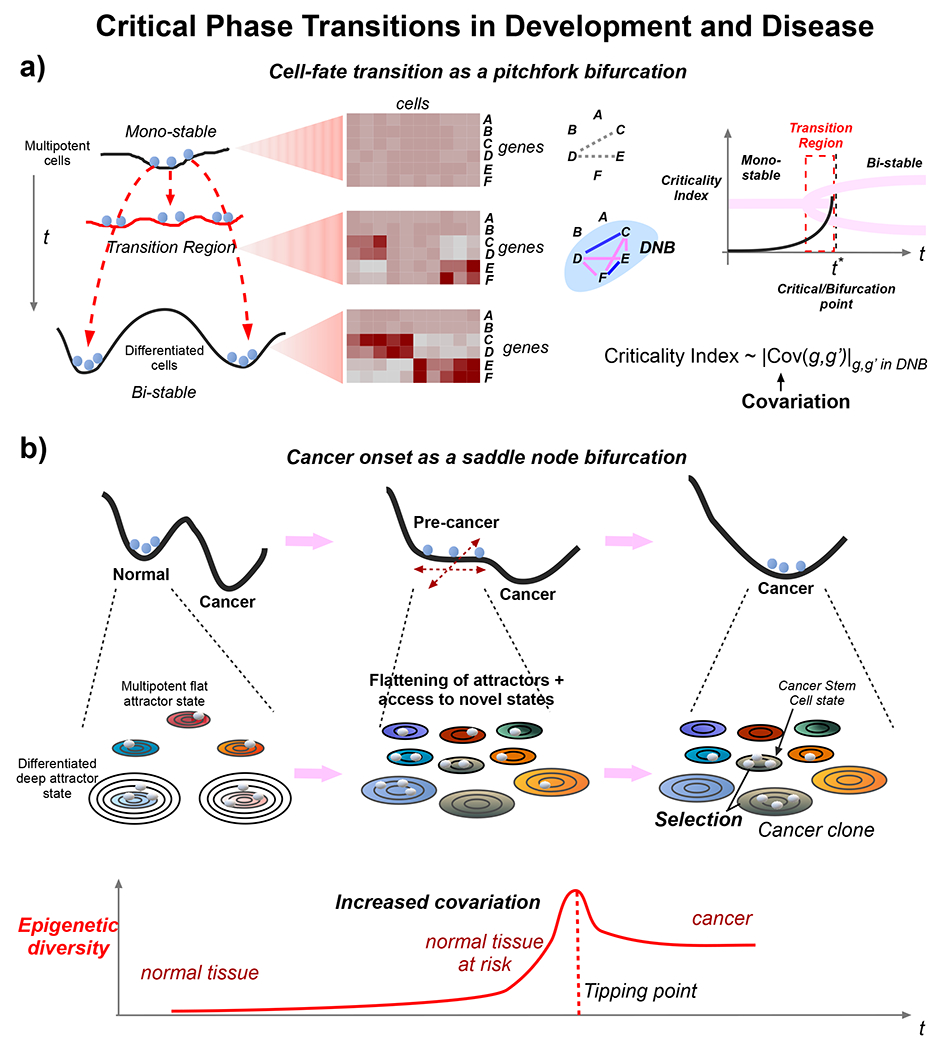
a. From a dynamical systems viewpoint, cell-fate transitions are described by dynamical bifurcations. Depicted is an example of a subcritical pitchfork bifurcation where a bipotent cell undergoes differentiation into one of two differentiated states. In the transition region the bipotent state becomes gradually destabilized while two meta-stable primed states emerge, defining a temporary region of tri-stability. Heatmaps of gene expression across cells and genes in the mono-stable, tri-stable and bi-stable regions are shown to highlight how particular genes exhibit increased covariation as the critical transition point is reached, reflecting increased interactions within a complex GRN. A universal principle of statistical mechanics predicts the existence of dynamic network biomarker (DNB), for which a criticality index measuring the covariation strength of gene pairs (g,g’) in the DNB (Cov(g,g’)) can be computed, and which increases as the critical phase transition point is approached. b. The transition of normal to cancer tissue can also be viewed as a critical phase transition and specifically as a saddle-node bifurcation in an appropriate dimension of phase-space (shown here along the x-axis as a one-dimensional space with the y-axis representing potential energy, top panel). Adding further phase-space dimensions to capture a more complete state-manifold, cancer progression can be seen as a gradual destabilization (lack of differentiation) of previously stable differentiated attractor states, and simultaneous emergence of new meta-stable attractors, increasing the epigenetic state diversity/mosaicism in a cell population. Each attractor is depicted as a series of concentric ellipses representing contours of stability with more circles indicating more stable attractors. Attractors containing cells indicate states present in the cell population (middle panel). Statistical mechanics predicts the existence of a DNB whose genes exhibit increased covariation due to the wider exploration of phase space states, and whose criticality index is a direct measure of the underlying epigenetic mosaicism. Cancer itself is characterized by the selection of a specific cancer clone that outgrows other precancer states, following e.g. acquisition of an oncogenic growth promoting driver event. As a result of this selection, epigenetic mosaicism drops, but still remains higher compared to the normal state (lower panel).

Experimental verification that cell-fate transitions do indeed exhibit the hallmarks of critical phase transitions and that criticality indices can be used to identify key regulators or markers controlling cell-fate, has come from a number of recent scRNA-Seq studies ^{91–93, 156}. In an experiment differentiating induced pluripotent stem cells (iPSCs) into induced cardiomyocytes, a criticality index was used to identify cKIT expression as a predictive marker for differentiation into the mesoderm cardiomyocyte lineage, as opposed to the competing endoderm lineage, thus providing a molecular basis for improving the efficiency of such reprogramming protocols ⁹¹. The phase transition model can also more naturally explain phenomena such as the presence of rebellious cells, i.e. cells that due to the destabilization of the multipotent progenitor state, can stochastically diffuse towards an unintended cell-fate, even in highly skewed differentiation protocols ⁹². While a limitation of these initial studies is that they only profiled a relatively small number of genes selected based on their perceived importance in the process under study ^91–93, recent genome-wide studies have provided further evidence for a phase transition model ^{83, 157}. For instance, using scM&T-seq ¹⁵⁸ to simultaneously profile the methylome and transcriptome in single cells, it was shown how multi-lineage priming and exit from pluripotency is associated with high intercellular variability in gene expression and enriched DNA methylation at putative enhancer sequences ¹⁵⁷.

Early warning signals for disease onset and progression.

An important application of the phase transition model is to disease risk prediction and prevention. Critical points underlying phase transitions often reflect underlying saddle-node bifurcations, which are irreversible, and therefore often referred to as tipping points ³ (Box-3, Fig.4b). They have been proposed as a model for disease onset and progression, describing the switch between healthy and disease states (Fig.4b) ¹⁵⁵. Thus, the increased covariation in molecular observables that accompanies the approach to criticality, provides an attractive framework in which to detect imminent tipping points. For instance, tipping points could occur in stages immediately prior to disease onset, where such onset could be avoided through appropriate preventive action ¹⁵⁴. In addition, the increased covariation and DNB could be used to identify disease risk biomarkers ¹⁵⁵. We stress that this represents a departure from the more common biomarker identification paradigm based on only seeking dynamic changes in average levels, and therefore represents a paradigm shift in how to select biomarkers.

A major challenge in applying this tipping-point concept to genomic medical data is the requirement, in theory, of many longitudinal measurements in the same individual. Although such a longitudinal approach is infeasible for diseases originating in inaccessible tissues, the DNB formalism can however also be applied ‘cross-sectionally’ across a training cohort of individuals from different disease stages to identify a DNB that can subsequently be used to predict disease risk in independent cohorts ¹⁵⁵. For instance, such a strategy was used on bulk DNA methylation data to predict the prospective risk of cervical cancer 3 years in advance of diagnosis ¹⁵⁹. In this context, the increased covariation is between specific CpGs in the DNB and in stages prior to cancer diagnosis, reflecting an increased epigenetic mosaicism within the cell population, which is maximal immediately before cancer onset ^{159, 160} (Fig.4b).

Statistical mechanical models exhibiting critical phase transitions have also been explored in a disease context at the single-molecule level ¹⁰⁷. By modellingspatially correlated DNA methylation patterns as derived from single molecule reads, in terms of a Boltzmann probability distribution with a potential energy function given by a, one-dimensional Ising-spin model, it has been possible to identify critical gene loci where alterations in DNA methylation could underpin an increased functional epigenetic plasticity and risk of cancer ^{107, 161}. The same Ising-spin model was used to infer that the genome is subdivided into regions of consistently low or consistently high methylation entropy, demonstrating that the boundaries of these “entropy-blocks” coincide with those of topologically-associated domains (TADs) ¹⁰⁷. This demonstrates how statistical mechanical models can lead to novel insight, in this case by deriving epigenetic entropy landscapes that associate with chromatin architecture, and elucidating principles by which these landscapes are altered in disease.

Future outlook and perspective

Statistical mechanics has already provided clear computational and conceptual advances when analyzing and interpreting single-cell data, yet its application to such data is still very much in its infancy. Although top-down modelling approaches such as PBA ⁴² and Waddington-OT⁴³ provide powerful paradigms for quantifying state-manifolds, they also possess intrinsic limitations, which can only be overcome by modelling the molecular complexity within single cells. Illustrating this, modelling single-cell data from the bottom-up using molecular entropy concepts has yielded reasonably accurate single-cell proxies for developmental potential, which have proved useful for identifying root and stem-like states, especially in the context of non-temporal or cancer scRNA-Seq data where the identification of these states is particularly difficult. Although some of these proxies have displayed good resolution, it is unclear how accurate they are for detecting primed states or distinguishing quiescent from activated states in pluri-and-multipotent populations. Further validation is therefore needed. It is also clear that current potency measures are imperfect, partly due to the technical noise of single-cell RNA-Seq assays, but also due to the relative simplicity of the underlying models. Novel strategies to smooth out noise, like those used in CytoTRACE ¹²¹, are needed, and should ideally also minimize the risk of overfitting. One possibility would be to integrate bottom-up and top-down modelling, for instance by iteratively solving drift-diffusion models for the potential energy function using the single-cell potency estimates from CytoTRACE ¹²¹ or SCENT ¹⁰¹ as input. Such integrative approaches remain uncharted territory. The complexity of the models being used must also increase, but only as far as they obey the principle of parsimony, also known as Occam’s Razor. An obvious direction to explore would be to consider incorporating additional epigenetic information (e.g. ATAC-Seq & DNA methylation), obtained from technologies such as scM&T ¹⁵⁸, sci-CAR ⁷⁶ or snm3C-Seq ¹⁶², that allow simultaneous measurement of multiple data-types in the same cell. Indeed, recent lineage-tracing technologies that have formally linked cell-progenitor states to cell-fate, indicate that sole reliance on mRNA expression may not be sufficient to fully predict cell-fate and that additional molecular information (e.g. chromatin states) may be needed ²⁶. Another possibility is to further refine the molecular network models, as motivated by the success of a method like SCENT ¹⁰¹, and where such refinements to say PPI networks are now increasingly possible thanks to protein subcellular localization efforts and more detailed and cell-type specific interactome mapping ^{163, 164}. More fundamentally, bottom-up single-cell measures based on entropy, RNA-velocity or gene-count provide a starting point in which to explain the ‘arrow of time’ in cellular development, offering a fresh orthogonal perspective to those derived from gene regulatory dynamics ⁴¹.

Although the original Waddington landscape has now given way to a more realistic and complex state-manifold ^15–17, visualization of essential features on these manifolds is important in order to build intuition, yet this remains a challenge. Current tools such as NetLand ¹⁶⁵ or Monte-Carlo based methods ¹⁶⁶ only offer visualization for manifolds associated with relatively low-dimensional GRNs, whilst there is an increased need for visualization of landscapes derived from large empirical scRNA-Seq datasets. A related outstanding challenge is the choice of most sensible phase space coordinates to use for analysis and visualization. Perhaps naively, current approaches treat all genes in the high-dimensional space on an equal footing, only using variability criteria to perform feature selection and subsequent dimensional reduction, yet in the context of development, differentiation and reprogramming, it is transcription factors that constitute the major players ⁷⁴. Thus, current tools for estimating regulatory activity in single-cells ⁷⁸ need to be improved in order to better characterize relevant phase space coordinates, and hence to improve the modelling of state-manifolds. Once again, integrative analysis of multi-modal single-cell data (e.g. DNA methylation/ATAC-Seq and gene expression) ^167–169 combined with orthogonal prior information (e.g. TF-regulons or binding-motif databases), may offer the best computational strategy to derive reliable regulatory activity maps that can serve as coordinates for subsequent phase-space representations. This is important in order to extend the construction of current local state-manifolds to global manifolds, which are necessary for predicting and understanding the outcomes of cell-fate reprogramming ¹⁷⁰ and organoid generation experiments ^{97, 171}, and which could be realized using techniques that integrate single-cell potency measures with infinite-range spin glass models ⁹⁸.

We envisage that statistical mechanical spin-glass models ¹⁷² will also play a fundamental role to help elucidate design principles underlying the spatial composition and distribution of cell-states in human organs. Such complex cellular ensembles are composed of several different cell types each distributed spatially according to a pattern dictated by intercellular communication signals and aimed at optimizing tissue-function. This is reminiscent of optimization problems that have been encountered in many other fields of science, from airline scheduling, to design principles in materials and semiconductor science, and therefore potentially amenable to analysis with the same spin-glass models that have found widespread application in these disciplines. Although not using a spin-glass per se, preliminary pioneering work in this direction used optimal transport theory to infer the spatial distribution of single-cells in complex tissues, using only scRNA-Seq data as input, thus pointing towards the existence of optimization design principles underlying spatial tissue architecture ¹⁷³. Spin-glasses may further help in modeling dynamic changes in spatial cellular architecture, such as those in development and disease. A type of spin-glass model known as a Markov random-field has already been used in combination with spatial single-cell transcriptomic mapping to help integrate single-cell transcriptomes with local patterns of intercellular communication to better understand the regulatory network principles controlling cell-identity ^{174, 175}. Experimental and computational advances in mapping intercellular communication ^176–178, for instance, as recently accomplished to uncover such communication between structural and immune cells ¹⁷⁹, will be important as a means of building more realistic spin-glass models of tissue function, as well as to dissect the relative roles of inter-and-intra cellular signaling in controlling cell-population features such as regulated stochasticity.

The ability to measure key molecular features at single-cell resolution means that the functions of single-cells can finally be understood within the context of the large spatial, dynamic and interacting cellular ensembles they form part of. Statistical Mechanics is set to help us achieve a deeper understanding of cell biological systems at multiple length scales, in the same way it has done so for materials science. We envisage an era of vibrant cross-pollination between these disciplines.

Key points:

• Stochastic Markov processes provide a powerful paradigm for inferring state-manifolds from single-cell dynamics.

• The need for more bottom-up modelling of single-cell data.

• Molecular entropy underpins differentiation potency of single-cells.

• Entropy-based estimation of single cell potency allows marker-free identification of root/stem-like states, and delineation of differentiation hierarchies.

• Statistical mechanics links microstate features of single-cells (e.g. molecular pluripotency) to macrostate cell population features (e.g. functional pluripotency).

• Cell-fate transitions exhibit the hallmarks of critical phase transitions.

• Increased covariation is a signal to identify cell-fate transitions and their regulators, in development and disease.

GLOSSARY:

Statistical Mechanics

A discipline of physics, which broadly speaking aims to describe macroscopic observables of a general system in terms of the properties of its microscopic constituents, including their interactions

Macrostate

A macroscopic observable of a system. Examples include electrical conductivity of a material, or the number of animals within an ecosystem

Microstate

The instantaneous and often dynamic state in which each microscopic constituent of the system is in, and which is often unobserved. Examples include the speed and direction at which each air molecule moves, or the electrical activity of each neuron in a brain

Phase transition

A phase transition is an abrupt, discontinuous change in the macroscopic properties of a system, often as a result of energy exchange with the environment, and driven by changes in the microscopic interaction patterns

High-throughput

In the context of single-cell technology, this means the ability to measure molecular properties in large numbers of cells, on the order of thousands to millions

Waddington epigenetic landscape

A 3-dimensional representation of cellular development, with differentiation trajectories and cell-states described by bifurcating valleys and local basins, and with the elevation in the landscape describing developmental potential

Differentiation potency hierarchy

The hierarchical arrangement of cell types, according to the number of downstream cell types a given cell could give rise to during development or in a general differentiation process

Potential energy

A term associated with the Waddington landscape, representing the elevation and correlating with developmental potential, in analogy with the physical potential energy associated with the elevation in geophysical landscapes

Dynamical systems theory

A branch of classical physics that describes the dynamics of multiple variables (e.g. molecular concentrations) in terms of a set of linear or non-linear differential equations

Regulatory network motif

It refers to the topological regulatory interaction pattern involving activation and/or inhibition between transcription factors, as specified in a gene-regulatory network

Single-cell omics

A generic term referring to a wide range of different technologies that can generate different types of molecular profiles at single-cell resolution, of which single-cell RNA-Seq and single-cell ATAC-Seq are two examples

Functional cellular state

The state of the complex molecular network within a cell that determines its function, encoded by a multi-dimensional vector describing properties such as cell-type, cell-cycle phase and metabolic state

State manifold

A generalization of Waddington’s landscape providing a more realistic geometric representation of functional cellular states and of the single-cell dynamics connecting these states

Feature selection

In the context of scRNA-Seq data analysis, this refers to a filtering step whereby all cells passing quality control are used to select genes according to some statistical criterion (e.g. high variability across cells)

Dimensional reduction

An analytical step in analysis of big data, including scRNA-Seq data, where a lower-dimensional representation of the data is sought that can capture a high proportion of the variance in the data

Bottom-up modeling

In the context of single-cell data, this refers to an analysis paradigm where one formulates an explicit dynamic (network) model to describe the data within each cell, often without the need to use data from other cells

Top-down modeling

In the context of single-cell data, this refers to an analysis paradigm where one analyzes the data from many cells together, to infer properties of individual cells

Dropout rate

This refers to the generally low sensitivity to detect gene expression in scRNA-Seq assays, specially for genes expressed at a low number of molecules in a cell, resulting in potentially many zero expression values

Quasi-potential

The name given to the scalar function obtained by solving sets of non-linear differential equations describing the dynamics of transcription factor concentrations, and which approximates developmental potential

Entropy

A generic term to quantify the amount of uncertainty associated with a system or the outcome of some measurement

Random walk

A stochastic Markov process on a finite discrete state space, often represented as nodes on a network/graph, and describing a trajectory along nodes, with transitions between nodes following a specific probability distribution

Mass-action principle

A physical law which states that the probability (rate) of a molecular interaction (reaction) is proportional to the product of the concentrations of each molecule (reactant)

Scale-free (network)

A type of network where the probability of finding a node with n neighbours decays according to a power law in n, i.e. it decays slower than an exponential function. The implication is that such networks contain network hubs

Hubs

Nodes within a network that possess an abnormally high number of neighbours. They define outliers in the degree distribution, and are a key feature of real biological networks including protein-protein-interaction networks

Gene-count

The number of expressed genes (i.e. number of genes with non-zero expression values) in a cell, as derived from a scRNA-Seq profile

Lineage trajectory

A one-dimensional trajectory in a high-dimensional phase space describing the dynamics of a cell, but often depicted graphically in a low-dimensional reduced space

Root state

In the context of inferring lineage-trajectories from scRNA-Seq data, this refers to the cell (or cluster of cells) where the trajectory starts, and which needs to be assigned before inference of trajectories can take place

Multi-lineage priming

In a cell population, this refers to the existence of some cells each one primed or restricted to differentiate into one of many downstream lineages

Funtional pluripotency

A term used to characterize pluripotency at the level of a cell population, and which refers to the ability of this population to give rise to cellular progeny of each of the 3 main germ layers

Phase space

An abstract space (usually high-dimensional) in which each point corresponds to a functional cellular state, with the dynamics of a cell’s state describing a one-dimensional trajectory in this space

Meta-stable

In the context of attractors, it refers to locally stable states, which however are not stable under higher-energy perturbations. Their stability is therefore often only transient

Stochastic

In relation to some variable, it refers to our inability to predict with certainty the value this variable would take if observed. This randomness can be due to incomplete knowledge or be inherent/intrinsic to the system

Stochastic process

A process describing multiple observations of a stochastic variable, often in time, or in some more abstract temporal space

Markov process

A memory-less stochastic process where the state of the system (e.g. cell) at any given timepoint is determined only by its immediately previous state

Markov Chain

A Markov process on a finite discrete state space (often a graph), defined by a probability matrix that describes the probabilities of transition between connecting states (in the graph context, these are the nodes)

Pseudotime

A temporal variable computed for each cell along a lineage trajectory, measuring the differentiation time from a given root state. It correlates with experimental differentiation stage and differentation potency but is also distinct

Cell-fate probability

The probability that a given cell will differentiate and give rise to progeny in a particular cell-fate, and which can be estimated from a Markov Chain description of single-cell dynamics

Optimal transport

A branch of mathematics that deals with optimizing the cost of transporting a distribution of mass (e.g. cells) between two successive locations, and which is amenable to solution via numerical programming

Least action principle

A variational principle derived from classical dynamics, where the dynamics of the system can be derived from the minimization of an energy function

Velocity field

In the context of scRNA-Seq data, a low-dimensional static graphical representation of cell dynamics, in which the future transcriptomic state of each cell is indicated by an arrow pointing away from the cell

TF-regulon

A regulon for a given TF consists of a set of direct (and possibly also indirect) targets of the TF and whose average gene expression provides a faithful measure of the TF’s regulatory activity

Spin-glass

A statistical mechanical model used to describe disordered physical systems composed of many interacting particles in a high-dimensional state-space and characterised by a relatively high number of equivalent low energy states

Order-parameter

A parameter of a statistical mechanical model, whereby varying this parameter can lead to transitions between different low-energy states

Correlation length

A term used frequently in statistical mechanics to describe the strength of correlations between neighboring microscopic elements (e.g. atoms/molecules) in a system, and which typically decays with distance or timepoint

Saddle-node bifurcation

A type of dynamical bifurcation associated with the emergence of an unstable “saddle-node” state in phase space, often termed a tipping point, and which has been proposed to describe the transition to a disease state

Infinite range spin-glass

A type of spin-glass where interactions can take place over very large distances encompassing the whole system

Ising-spin model

A special case of a spin-glass where interactions are localized to nearest neighbors and where the state-space of each particle is only 2-dimensional

Occam’s Razor

Also called law of parsimony, is a principle stated by the philosopher William of Ockham (1285–1347) that gives precedence to simplicity: of two competing theories, the simpler explanation of an entity is to be preferred

Global manifold

The global manifold refers to the complete state manifold encompassing all developmental stages and cell types within a given organism, to be distinguished from local state-manifolds that only refer to specific subparts