Figure 2:

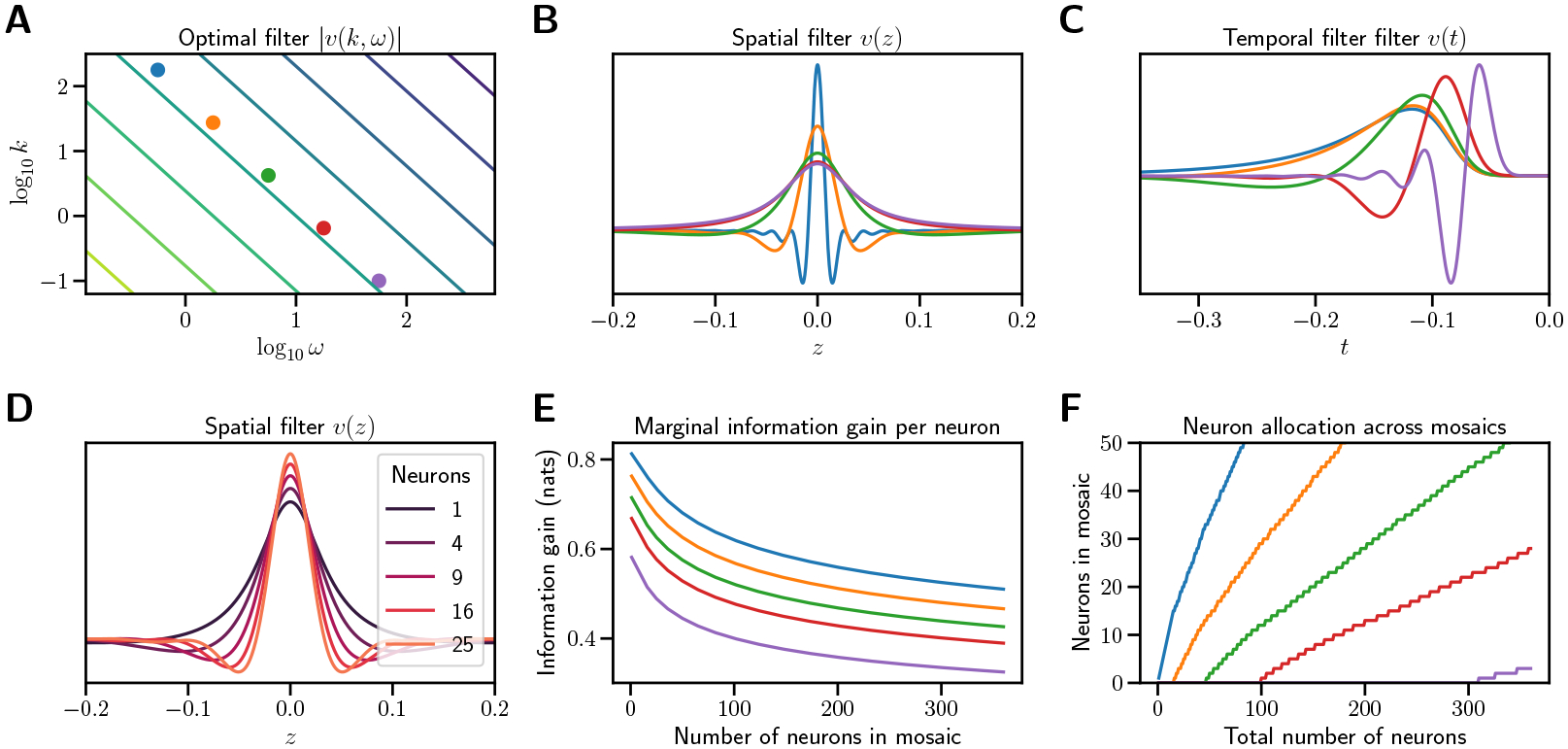
Optimal filters in the linear spacetime case. (A) Spectrum of the optimal linear spacetime filter in $d=1$ spatial dimension. Contour lines indicate constant (log) power. (B) Spatial filters at representative temporal frequencies. Each filter represents a vertical section at the correspondingly colored dot in A. (C) Temporal filters at representative spatial frequencies. Each filter represents a horizontal section at the correspondingly colored dot in A. (D) Spatial filters at $\omega =0$ for increasing numbers of RGCs $J$. The spatial extent of the center narrows with more RGCs added to the mosaic. (E) Gain in information per RGC added to each mosaic as a function of current RGC number $J$. New cell types begin when the marginal benefit of adding an RGC to an existing mosaic equals the benefit of adding the first RGC of a new cell type. Color indicates ${\omega }_0$, the temporal frequency of the narrow-band filter. (F) Total number of RGCs in each mosaic as a function of total RGCs across all mosaics. As new cell types arise and form mosaics, new RGCs are allocated to existing mosaics at a decreasing rate. For both plots, $A=100,{\sigma }_{\text{in}}=0.4,{\sigma }_{\text{out}}=1.25$, and ${\text{log}}_{10}{\omega }_0=1.5,1.52,1.54,1.56,1.6$. Details of calculations in Appendix A.5.