Natural cubic splines for the analysis of Alzheimer’s clinical trials

Abstract

Mixed model repeated measures (MMRM) is the most common analysis approach used in clinical trials for Alzheimer’s disease and other progressive diseases measured with continuous outcomes over time. The model treats time as a categorical variable, which allows an unconstrained estimate of the mean for each study visit in each randomized group. Categorizing time in this way can be problematic when assessments occur off-schedule, as including off-schedule visits can induce bias, and excluding them ignores valuable information and violates the intention to treat principle. This problem has been exacerbated by clinical trial visits which have been delayed due to the COVID19 pandemic. As an alternative to MMRM, we propose a constrained longitudinal data analysis with natural cubic splines that treats time as continuous and uses test version effects to model the mean over time. Compared to categorical-time models like MMRM and models that assume a proportional treatment effect, the spline model is shown to be more parsimonious and precise in real clinical trial datasets, and has better power and Type I error in a variety of simulation scenarios.

1 |. BACKGROUND

The mixed model repeated measures (MMRM)¹ is a common analytic approach for randomized clinical trials with continuous outcomes collected longitudinally. The MMRM generally assumes that the mean change from baseline in the outcome is a linear function of the baseline value of the outcome, time (as a categorical variable reflecting timing of study visits), and the time-by-treatment interaction. This allows an estimate of the mean at each visit for both groups without assuming any trend over time. The primary test statistic is typically the estimated difference between group means at the final visit. The model generally includes no random effects. Instead, residuals are assumed to be correlated from visit-to-visit within participant. The MMRM is virtually assumption-free concerning the shape of the mean over time and the correlation structure, which likely explains its broad use in pharmaceutical statistics.

However, the MMRM requires many parameters. If K is the number of visits, MMRM requires 2K mean parameters, K(K − 1)/2 correlation parameters (assuming a general symmetric correlation structure), and K variance parameters (assuming heterogeneous variance). In this respect, MMRM might be seen to be favoring reduced bias at the cost of statistical efficiency and power.

Another concern is that clinical trial visits often occur off-schedule. Study protocols generally allow a visit window (e.g. visits may occur within two weeks of a target date). When observations fall outside these windows, investigators are forced to decide between ignoring data or including it and introducing potential bias due to observations being effectively carried forward or backward to the closest target date². The problem of late visits can be exacerbated by unforeseen interruptions, such as those caused by the COVID19 pandemic. In these situations, it might be advantageous to treat time as continuous, thus allowing the model to be informed by the actual time from baseline, rather than categorized time.

Alzheimer’s clinical trials often employ alternating cognitive test versions (e.g. alternating stories or word lists to be recalled). These test stimuli versions typically alternate with the visit schedule such that all study participants should be administered the same sequence of test versions per protocol. The versions are intended to be of similar difficulty. However, differences in difficulty are apparent by the sawtooth mean trends, synchronized between treatment groups, estimated by MMRM in many Alzheimer’s trials. Assuming a smooth parametric mean trend for continuous-time might fail to capture this explainable variability.

An alternative to MMRM was proposed for clinical trials in autosomal-dominant Alzheimer’s disease^3,4. The time variable is the expected year of symptom onset (EYO) and the placebo group mean is modeled as a monotonically decreasing step function of EYO. The treatment benefit is assumed to be proportional to the decline, making the model nonlinear. The model was extended to a multiple outcome model for the final analysis, but the monotonicity and proportional treatment effect assumptions were violated and the model failed to converge⁵. More recently, related nonlinear models have been proposed for clinical trials for sporadic Alzheimer’s disease by Wang, et al⁶ and Raket⁷.

In this paper, we explore another alternative model for Alzheimer’s disease trials, one that treats time as continuous. We consider natural cubic splines⁸ to flexibly model the temporal mean trend with fewer parameters than MMRM. Incorporating splines into random effects models for longitudinal data, and clinical trials in particular, is not novel^9,10,11. We compare a natural cubic splines model to categorical-time models (MMRM) and models assuming a proportional treatment effect in three completed Alzheimer’s studies and in simulations. We also explore the utility of adjusting for alternating cognitive test versions with a time-varying covariate. A simulation study is presented to demonstrate the power and Type I error of each approach. The spline model is shown to provide superior power with good control of Type I error.

2 |. MODEL SPECIFICATIONS

Categorical-time mean structure.

The first type of mean structure treats time as a categorical variable, as in the MMRM. The response for subject i and study visit j = 1, … , K is modeled as:

$$\begin{gathered} Y_{ij}={\beta }_{1}1\{j=1\}+{\beta }_{2}1\{j=2\}+\cdots +{\beta }_{K}1\{j=K\}+ \\ \left({\gamma }_{2}1\{j=2\}+\cdots +{\gamma }_{K}1\{j=K\}\right){\text{Active}}_i+{\epsilon }_{ij} \end{gathered}$$

where “Active_i” is 1 if subject i is in the active group and 0 otherwise. The β terms express the mean at each visit in the placebo group (e.g. the estimated placebo group mean is ${\widehat{\beta }}_1$ at baseline and ${\widehat{\beta }}_2$ at the first follow-up) and the γ terms represent the treatment group difference at each visit. We focus here on the temporal mean structure, but other baseline covariate effects can be added with additional terms as usual. Note that the exclusion of a γ₁ term constrains the mean at baseline to be the same for both groups. This is the constraint referred to in constrained longitudinal data analysis (cLDA)¹². This categorical-time mean structure is similar to MMRM, but in MMRM the response variable is the change from baseline, $Y_{ij}^{*}=Y_{ij}-Y_{i1}$, for j = 2, … , L; the baseline score Y_i1 is included as a covariate; and the β₁1{j = 1} term is dropped. The cLDA parameterization is more efficient than MMRM when baseline observations are subject to missingness¹³. We explore several different variance-covariance structures for the residuals ε_ij as described at the end of this section.

Linear mean structure.

Alternatively, time from baseline at visit j can be treated as a continuous variable t_j. The linear mean structure assumes:

$$Y_{ij}={\beta }_0+{\beta }_1{t}_j+\gamma t_j{\text{Active}}_i+{\epsilon }_{ij}.$$

The β₀ term represents the mean in both groups at baseline, β₁ represents the rate of change per month in the control group and the γ term represents the difference in slopes.

Natural cubic spline mean structure.

The natural cubic spline⁸ structure also treats time as continuous. A cubic spline is a function defined by cubic polynomials that are spliced together at knot locations and the resulting function is restricted to be continuous and have continuous first and second derivatives. A natural cubic spline has a further constraint of having a second derivative of zero at the boundaries (i.e. acceleration of the curve is not allowed at the first and last observation). A spline function f(t) can be expressed as a linear combination of basis functions, b_k(t), and weights ${\beta }_k:f(t)={\beta }_0+{\sum }_{k=1}^m{\beta }_k{b}_k(t)$. The b_k(t) basis functions can be numerically determined given the boundaries, interior knot locations, and the continuity and derivative constraints. In practice, this is a processing step that does not involve the observed outcomes, akin to calculating t², t³, etc. for polynomial regression. As with polynomial regression, once the b_k(t) are determined, the β_k weights can be estimated by maximum likelihood estimation.

In our clinical trial context, the natural cubic spline model assumes:

$$Y_{ij}={\beta }_0+\sum _{k=1}^m{\beta }_k{b}_k\left(t_j\right)+{\text{Active}}_i\sum _{k=1}^m{\gamma }_k{b}_k\left(t_j\right)+{\epsilon }_{ij}.$$

where b_k(t) are the known spline basis functions for a given set of knots and extreme values of t. Interior knots are typically spaced according to quantiles of t. The resulting curve for the placebo group is defined by the natural cubic spline $f(t)={\beta }_0+{\sum }_{k=1}^m{\beta }_k{b}_k\left(t_j\right)$; while the natural cubic spline $g(t)={\sum }_{k=1}^m{\gamma }_k{b}_k\left(t_j\right)$ represents the treatment group difference over time and is constrained to be zero at time zero. The number of interior knots (m − 2) needs to be specified. Given the known basis functions, estimation of the unknown parameters (βs and γs) is accomplished with maximum likelihood estimation as with the prior two models. Note that the categorical-time mean structure is equivalent to a special case of the spline parameterization with visit times set to the planned times and knot locations chosen to match the planned visit times.

Again, as with the other temporal mean structures, additional covariates can be added. In particular, we will add a time-varying covariate for cognitive test version. The time-varying covariate effect can be interpreted as a version difficulty offset and can be added to the models that assume a suitably smooth parametric tend over time. We also explore adding the test version effect to categorical-time models, however, we would not expect this to have a large impact because test versions alternate with the visit categories by design.

Cognitive test version at time t is clearly an exogenous variable, independent of values of the assessment before time t, and should not bias or otherwise interfere with the interpretation of the treatment effects¹⁴. The schedule of test versions is typically entirely determined by the protocol and any deviations from the protocol are due to administration errors unrelated to prior test performance. Nevertheless, an alternative strategy would be to adjust the scoring rules for the test version’s difficulty level using data external to the trial.

Proportional treatment effect.

The proportional treatment effect model is of the form

$$Y_{ij}={\beta }_0+\left({\beta }_{1}1\{j\ge 1\}+{\beta }_{2}1\{j\ge 2\}+\cdots +{\beta }_{K}1\{j=K\}\right)\exp \left(\theta {\mathrm{Active}}_i\right)+{\epsilon }_{ij}.$$

The mean structure assumption for the placebo group is equivalent to the categorical-time model above, but the active group is assumed to differ at every visit by a constant factor of exp(θ).

Variance-covariance assumptions.

Since the mean structures in this paper treat time as either categorical or continuous, we explored variance-covariance assumptions under both paradigms as well. The considered variance-covariance assumptions include:

• Unstructured: The vector of residuals for individual i ε_i are assumed to follow a multivariate Gaussian distribution with mean zero and general symmetric correlation and heterogeneous variance per study visit: ${\epsilon }_i~𝒩(0,V\mathrm{\Sigma }V)$ for diagonal matrix V and symmetric general matrix Σ,

• “AR1 Het.”: categorical-time autoregressive order one correlation with heterogeneous variance per visit,

• “CAR1 Const. Prop.”: continuous-time autoregressive order one correlation with variance function consisting of a constant a and proportion $b:\mathrm{Var}({\epsilon }_{ij})=a^2+b^2{t}_{ij}^2$, where t_ij is continuous-time from baseline,

• “CAR1 Exp.”: continuous-time autoregressive order one correlation with Var(ε_ij) = σ² exp(2δt_ij),

• “Random Intercept”: participant-specific random intercepts with independent and identically distributed Gaussian residuals, and

• “Random Slope”: participant-specific random intercepts and slopes relative to t_ij with independent and identically distributed Gaussian residuals.

• “Random Spline”: participant-specific random terms associated with the natural cubic spline basis expansion and identically distributed Gaussian residuals. In this paper, we only consider two degrees of freedom for the random spline.

All of the above variance-covariance assumptions and their estimation are detailed in Pinheiro and Bates¹⁵. Non-linear models are fit by maximum likelihood estimation using the nlme package¹⁶ in R¹⁷. Linear models with unstructured variance-covariance are fit with the lme4 package¹⁸, and other covariance structures are fit with gls function in the nlme package. The emmeans package¹⁹ is used for estimating the means and contrasts of linear models over time with Sattherwaite degrees of freedom, while parametric resampling of fixed effects (based on their estimated mean and covariance) is used for the nonlinear models. The ggplot2 package is used for plotting²⁰. Sample code for the simulation study is provided in the Appendix.

3 |. MODEL DEMONSTRATIONS

We demonstrate applications of the models using three completed Alzheimer’s disease (AD) clinical trials. The first is the study of Donepezil and Vitamin E for Mild Cognitive Impairment (MCI)²¹. For these analyses, we focus on the data from participants randomized to Donepezil or placebo. The second is a study of the fyn kinase inhibitor AZD0530 in mild Alzheimer dementia²². The third is a study of intranasal insulin in MCI and mild Alzheimer dementia²³. Two intranasal devices were used in this study because the first was unreliable. We focus on data from the second device.

None of these studies met their primary endpoint, but Donepezil showed a benefit in the first months of the MCI trial that seemed to diminish by the final 36-month time point. The primary analysis approach for the MCI trial was a Cox proportional hazard model²⁴ of time-to-dementia, however, the proportional hazard assumption was violated. For all three trials, we demonstrate the modelling approaches using the Alzheimer’s Disease Assessment Scale–Cognitive Subscale (ADAS-Cog)²⁵. For the MCI trial, we see violations of the proportional treatment effect assumption for ADAS-Cog as well.

Figure 1 shows the estimated mean trends from each study using the four approaches assuming unstructured variance-covariance. We can see that the spline model with two degrees of freedom (one interior knot) and a time-varying effect for test version estimates trends that are very similar to the categorical-time model (left); while the proportional effect models demonstrate less separation between groups in Fyn and MCI. The proportional effect model estimates the effect in the MCI trial to be in the opposite direction of all the other models, perhaps due to the violation of the proportional effect assumption.

FIGURE 1.

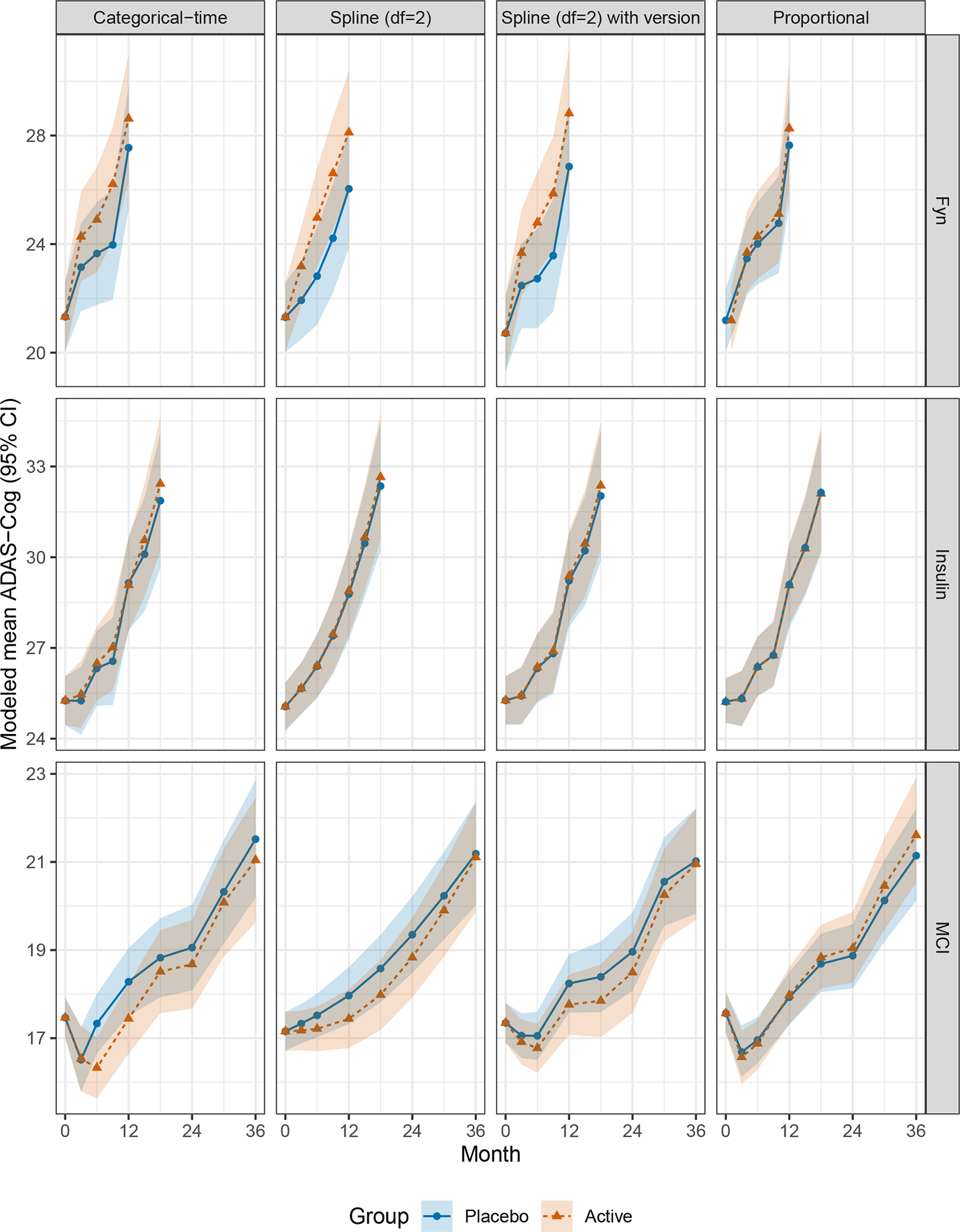
Modeled mean ADAS-Cog for each study. All models assume unstructured variance-covariance.

ADAS-Cog, Alzheimer’s Disease Assessment Scale–Cognitive Subscale; MCI, Mild Cognitive Impairment

Figure 2 shows the treatment group contrast over time as estimated by the four approaches in the three trials. In general, the spline model appears to be a reasonably smoothed version of the trend estimated using categorical-time; while the proportional treatment effect model fails to show consistent mean trends where these assumptions are violated (i.e. the Fyn and MCI studies) and treatment effect estimates seem biased toward the null relative to the other models applied to Fyn and Insulin. And, again we see the proportional effect model estimating an effect in the opposite direction of other models when applied to the MCI trial.

FIGURE 2.

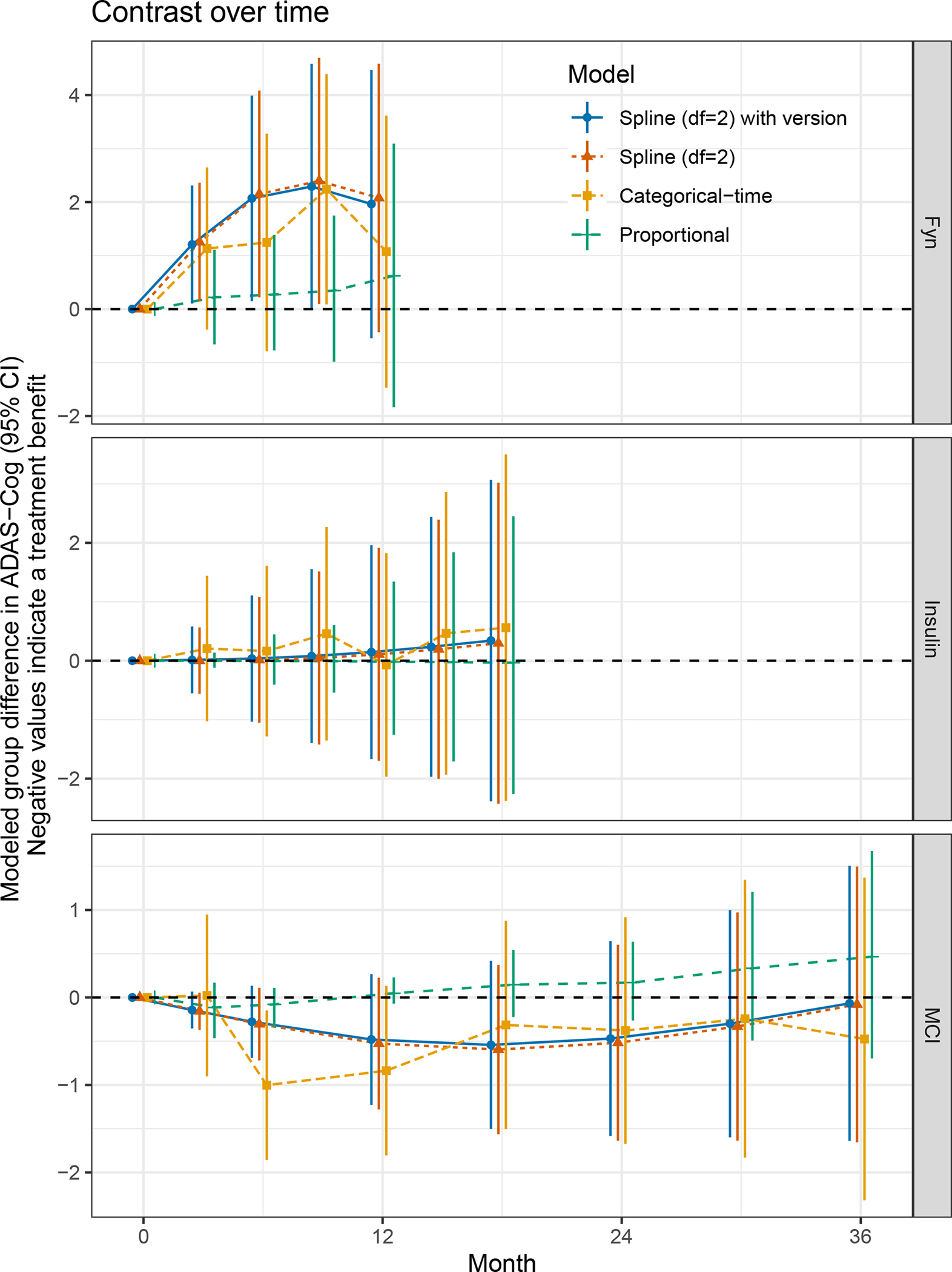
Modeled treatment group contrast in ADAS-Cog for each study. All models assume unstructured variance-covariance.

ADAS-Cog, Alzheimer’s Disease Assessment Scale–Cognitive Subscale; MCI, Mild Cognitive Impairment

We also considered Akaike Information Criterion²⁶ for each model estimated by maximum likelihood to assess relative parsimony and predictive value (Figure A1 and Table A1). In general, the categorical-time unstructured variance-covariance assumption was preferred even with continuous-time mean structures, followed closely by the random slopes assumption. Focusing on models assuming unstructured variance-covariance (bottom panel), the spline model with two degrees of freedom (one interior knot) and version effect attained the smallest AIC for the Fyn and Insulin studies. The proportional model was preferred for MCI, but the proportional effect assumption is violated in this trial and the resulting treatment effect estimate is in the opposite direction of other models. Considering that the spline with two degrees of freedom and version effect provide fits that are similar to categorical-time in Figure 1, we concluded that two degrees of freedom appear to be sufficient to capture enough of the general trend to assess the treatment effect.

The AIC comparisons also show that adding an ADAS-Cog version effect to the spline model with two degrees of freedom provides a substantial and consistent reduction in AIC (−13.2, −5, −17.4 AIC points for the Fyn, Insulin, and MCI trials respectively using unstructured variance-covariance). Of note, the categorical-time model without version effect is preferred over the spline with two degrees of freedom for Fyn and MCI. But once the version effect is added, the spline with two degrees of freedom is preferred over categorical in all three studies. Adding a version effect to the categorical-time model increased AIC or only reduced AIC by a point (3.4, −1, 1.7 AIC points respectively).

4 |. SIMULATION STUDIES

We consider four simulation scenarios: (1) MCI or mild Alzheimer dementia (n=120 per group), (2) MCI only (n=250 per group), (3) Preclinical Alzheimer’s Disease (PAD, n=500 per group), and (4) PAD with a COVID19 pandemic disruption in follow-up (n=500 per group). The first two are derived from the Insulin and MCI studies respectively. Actual participant data regarding baseline covariates (APOE ϵ4 genotype, Mini-Mental State Exam [MMSE], age) and follow-up (administered test version [A, B, or C] and missing data) were used. Within each simulated trial, group assignments are permuted. Note that the simulated visit schedules are consistent with the depiction in Figure 1 (0, 3, 6, 9, 12, 15, 18 months for Insulin and 0, 3, 6, 12, 18, 24, 30, 36 for MCI). Simulated placebo group outcome data is generated according to a natural cubic spline model fit to the study data. The model assumes splines with four degrees of freedom (three interior knots), and covariates for baseline MMSE, APOE ϵ4 genotype, and age. Residuals are assumed to have unstructured heterogeneous variance-covariance. The Insulin model also includes an effect for sex. We do not simulate data from an MMRM because we want the simulated data to be informed by actual time from baseline. The choice of four degrees of freedom for the simulation model is an arbitrary one intended to differ from the candidate natural cubic spline analysis model with two degrees of freedom.

The treatment benefit for the MCI study is assumed to be linear, starting at 12 months, reaching a relative benefit of 2.75 ADAS-Cog points at month 36. This delayed onset of treatment benefit might be expected from a disease modifying therapy, as opposed a symptomatic therapy like Donepezil. For the simulation of a trial in MCI or mild Alzheimer dementia we assume an immediate linear benefit of 4.25 ADAS-Cog points for the 18-month study, which might be expected from an intervention like insulin which is believed to have the potential for symptomatic and disease-modifying effects.

The last two simulation studies are based on Preclinical Alzheimer’s Cognitive Composite (PACC)²⁷ data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI; adni.loni.usc.edu) cognitively normal subjects with evidence of brain amyloid dysregulation, so-called Preclinical Alzheimer’s Disease (PAD). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biomarkers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. The simulated PAD trials include ten study visits targeted every six months for 4.5 years. The simulated observation times are randomly perturbed, centered around the target time point, according to a normal distribution with standard deviation of 0.8 months. We also simulate a hypothetical PAD trial disrupted by COVID19. The COVID interruption is simulated to start randomly, based on a random sample of the last six visits, and subjects return to regular visits after a random duration distributed according to a truncated normal distribution with mean six months, standard deviation three months, and range four to twelve months. Code for this simulation is provided in Appendix B, including the ADNI-derived model parameters needed to replicate the simulation. The treatment benefit for both PAD studies is assumed to be linear relative to the visit number, starting at the fourth visit, and attaining 1.6 PACC points at the tenth and final visit. This diminishes the treatment effect relative to time-from-baseline, as might be expected if doses are missed because of the COVID interruption. Monotone attrition is simulated yielding 30% dropout rate by the final visit. See Appendix Figure A2 for estimates of the simulated treatment effects estimated from typical simulated trials.

Each of 10,000 simulated trials is analyzed with three mean structures: a categorical-time model, a natural cubic spline model with two degrees of freedom and test version effect, and a model assuming a proportional treatment benefit. The categorical-time model assumed unstructured heterogeneous variance-covariance. The spline model assumed four different variance-covariance assumptions: unstructured heterogeneous, random slope, random spline, and continuous-time autoregressive order one with exponential variance function of time. The proportional model assumes a random participant-specific intercept and independent residuals (as described by Wang et al.⁴), or correlated residuals with unstructured heterogeneous variance-covariance. The inference for the categorical-time model is based on the final visit treatment group mean contrast. The inference for the spline model is based on the final target time point (i.e. 18 months for Mild AD or MCI, 36 months for MCI only, and 54 months for both PAD trials). The inference for the proportional model is based on the estimated proportional treatment effect (which the model assumes to be constant over time). The Satterthwaite degrees of freedom were used for all contrasts, except for the PAD simulations. Due to computational time of the PAD simulations, Satterthwaite degrees of freedom were only calculated for the first 100 simulated trials, and for subsequent simulations, the minimum degrees of freedom estimated from the first 100 trials was assumed.

Table 1 summarizes the simulation results. The spline and categorical-time models with unstructured variance-covariance provide reasonable control of Type I error (<5.56%) and the spline model demonstrated modest to substantial improvement in power in all scenarios without convergence issues. The spline model improved power relative to the categorical model by 4.37% in the Mild AD or MCI simulation, 9.65% in the MCI only simulation, 16.07% in the PAD simulation, and 13.42% in the PAD-COVID simulation.

TABLE 1.

Simulated power and type I error. Mild AD dementia or MCI and MCI only simulations were based on patient characteristics and model estimates from the Insulin and MCI trials. The PAD simulations are based on patient characteristics and model estimates from ADNI participants. The PAD-COVID simulations add a random interruption in study visits and treatment due to COVID19. The Spline model is based on natural cubic splines with one internal knot and a time-varying test version effect. The number of trials in which a p-value was obtained is indicated by N.

	Power		Type I Error
Model	%	N	%	N
Mild AD or MCI; n=120 per group
Categorical time	82.29	10000	5.16	10000
Spline-Unstr.	86.66	10000	5.41	10000
Spline-Random slope	86.10	10000	5.18	10000
Spline-Random spline	85.81	10000	4.96	10000
Spline-CARl	82.37	10000	6.69	10000
Proportional-Random int.	95.35	9882	30.32	10000
Proportional-Unstr.	93.00	9204	64.95	9268
MCI only; n=250 per group
Categorical time	85.32	10000	5.17	10000
Spline-Unstr.	94.97	10000	5.40	10000
Spline-Random slope	94.48	10000	5.18	10000
Spline-Random spline	94.47	10000	5.14	10000
Spline-CARl	84.15	10000	7.73	10000
Proportional-Random int.	97.08	9788	27.90	10000
Proportional-Unstr.	94.34	8947	62.77	9204
PAD; n=500 per group
Categorical time	77.23	10000	4.98	10000
Spline-Unstr.	93.30	10000	5.56	10000
Spline-Random slope	93.92	10000	10.73	10000
Spline-Random spline	91.60	10000	5.24	10000
Spline-CARl	90.81	10000	8.44	10000
Proportional-Random int.	18.52	3331	27.26	9801
Proportional-Unstr.	99.91	3388	91.22	9444
PAD-COVID; n=500 per group
Categorical time	78.38	10000	5.30	10000
Spline-Unstr.	91.80	10000	5.34	10000
Spline-Random slope	92.52	10000	7.06	10000
Spline-Random spline	92.75	10000	5.38	10000
Spline-CARl	90.96	10000	8.23	10000
Proportional-Random int.	25.18	2407	35.28	9980
Proportional-Unstr.	98.24	1766	93.92	9691

MCI, Mild Cognitive Impairment; AD, Alzheimer’s Disease; PAD, Preclinical Alzheimer’s Disease; ADNI, Alzheimer’s Disease Neuroimaging Initiative; CAR1, continuous-time autoregressive order one correlation with exponential variance function of time; Unstr., unstructured variance-covariance

In contrast, the proportional treatment effect model suffered from Type I error inflation in all scenarios, with Type I error ranging from 27.26% to 93.92%. The proportional model was also plagued by model fitting issues and provided an inferential statistic in only 2407/10000=24.07% of simulated PAD-COVID trials. Note that the PAD scenarios assumed non-proportional treatment effects with a delayed onset and placebo mean trends which might cross zero; which might explain why the model did not converge consistently. The proportional model did not fail to converge as often with the Type I error simulations, with no treatment effect. Type I error was larger than the power in some scenarios, perhaps an artifact of the convergence issues. The Type I error remained inflated for the proportional model even when models with convergence warnings were removed (Appendix Table A2). Other simulations studies assuming proportional effects have not reported convergence problems with related proportional models^6,7, however, Type I error inflation has been previously reported⁷.

5 |. DISCUSSION

While models with proportional treatment effects have attracted attention as a purported powerful alternative to MMRM for AD clinical trials, the model assumptions are often violated and the models appear to be subject to severe Type I error inflation and convergence problems when its assumptions are violated. It is important to note that the proportional treatment effect assumption is a strong assumption that links benefit to placebo decline and can be violated in many ways. A disease modifying effect could demonstrate a divergence from the placebo trend in many ways that are not proportional. For instance, a linear trend benefit would only satisfy the assumption when the placebo trend is also linear.

In contrast, spline models have weaker assumptions regarding the nature of the placebo decline and treatment effect and can generally be fitted with the same software used to fit linear models like MMRM. The weaker assumptions of the spline model allow a broad possibility of treatment effects that are not restricted to be linear or proportional relative to the placebo group mean.

The spline models also show a modest to substantial improvement in power (4.37% to 16.07%) compared to categorical-time models and provide reasonable Type I error control. The power increase is likely due to the reduced variance of estimates from the simpler spline model. The increase in power seems to be larger for study designs with more visits, as one might expect since this increases the complexity of the categorical-time mean parameterization.

Because the spline model treats time as continuous, it can accommodate delays in study visits, such as those due to the COVID19 pandemic. With a categorical-time model, investigators must choose between ignoring delayed visits, carrying observations back, or creating new visit categories with depleted observation counts and a mixture of test versions. The spline model also showed greater power to detect treatment effects compared to the categorical-time model in the simulated trials with a COVID19 disruption.

In absence of the COVID19 interruption, the MMRM is targeting the randomized group mean difference at 4.5 years. Under the model in which participants are invited back for all visits after the interruption, an MMRM analysis ignoring the COVID19 delay in visits is targeting a different estimand: the randomized group mean difference after nine irregularly spaced follow-up visits. The test statistic that we explored in the spline analysis, the treatment group difference at 4.5 years, is therefore more consistent with the uninterrupted study’s original estimand.

A drawback of the spline model is the need to specify the number and location of interior knots. In these analyses, we followed the default software setting, which equally spaces the knots according to the quantiles of observation times. Of note, the number of knots is understood to be more important than their location, and using quantiles for knot locations is a broadly recommended approach²⁸. The natural cubic spline with one interior knot at the median observation time seems sufficient in the trials and datasets that we explored. Conceptually, one interior knot captures quadratic-like trends with one inflection point for the placebo group and another for the relative treatment difference. We believe this degree of flexibility is sufficient to capture the expected trends in Alzheimer’s clinical trials. More exploration might be required in other applications to ensure a suitable choice of knot locations. Prior clinical trials or natural history studies can be used to guide this decision, which should be pre-specified in analytic plans.

While unconventional, it appears the combination of categorical-time covariance structures and continuous-time mean structure is generally preferred and supported by AIC in the trials analyzed. We hypothesize that this is because of the categorical nature of the Alzheimer’s clinical trial visit schedule in which study participants undergo the same sequence of visits and cognitive test versions. The simulation studies demonstrate better Type I error control for the spline models with unstructured variance-covariance (≤ 5.56%) or random spline (≤ 5.38%) relative to random slope (which had Type I error as large as 10.73%) and continuous-time autoregressive order one with exponential variance function of time (which had Type I error as large as 8.44%). Our simulations included some exploration of misspecification of the variance-covariance, but only when the true model was assumed to have an unstructured variance-covariance. Sandwich estimators may also be used to provide standard errors that are robust to misspecification of the variance-covariance^29,30, however, we found this to have negligible effect in the trials analyzed (Figure A3).

A limitation of this work is that we have focused exclusively on estimation of the treatment policy estimand using all available observations submitted to maximum likelihood estimation. These estimates should be robust and unbiased assuming data are missing at random, though missing not at random processes were not explored. Polverejan et al.³¹ discuss some alternative estimands and an estimation procedure based on multiple imputation for Alzheimer’s clinical trials in the face of data missing not at random relative to treatment discontinuation and initiation of other therapies. They demonstrate that maximum likelihood estimators could be biased when on- and off-treatment mean trajectories differ.

However, we have found that the intuition underlying some hypothetical estimands and their estimation approaches can be problematic. For example, intuition might lead one to believe that mean performance on a cognitive measure would be improved after the initiation of symptomatic medication for Alzheimer’s compared to individuals not initiating symptomatic medication. And therefore, we might choose to ignore observations after symptomatic medication and target a hypothetical estimand for the experimental treatment benefit in absence of the symptomatic medication. Contrary to this intuition, in individuals with mild cognitive impairment, allowing observations after the initiation of symptomatic medication results in worse cognitive trajectories than censoring those observations³². This is likely because individuals are prescribed medication due to their precipitous decline, and the benefit conferred by the medication is not enough to improve that decline above and beyond those who are not prescribed medication. Therefore we prefer targeting a treatment policy estimand that is estimated using as much post-randomization data as possible (regardless of intercurrent therapy) submitted to an appropriate model under the assumption of data missing at random, and assess the sensitivity to data missing not at random with a delta method tipping point analysis³³. In Appendix C, we demonstrate how this can be done using two-level imputation models with the mice R package³⁴. This strategy can also be adapted to use the NCS model to target the estimands explored in Polverejan et al.³¹. This would require perturbing imputations according to intercurrent events, rather than simply perturbing all imputations in the active group by the same amount, as in the tipping point approach.

Another limitation is that we have not systematically altered the degree to which visits are off-schedule and the magnitude of version effects. Simulating visit which are further off-schedule might tend to favor the spline model more, and vice versa. Similarly, simulating reduced version effects might demonstrate diminishing returns from including this effect in the model. Instead, we simulated visit intervals observed in actual Alzheimer’s trials, or anticipated due to COVID interruptions, and estimated version effects from actual Alzheimer’s trials. Therefore, we are reasonably assured that the results are relevant for these trials. We recommend additional simulation studies for those interested in comparing spline models to MMRM in other therapeutic areas with different outcome measures and study design characteristics. When we fit the spline models using the scheduled or target time from baseline (not shown), we found that AIC was the same (for MCI and Insulin) or three points larger (Fyn) than when using actual time. This suggests that for these trials, the spline structure itself might be conferring more of the model improvement than the use of actual time.

Overall, the natural cubic spline framework exhibits several advantages and very few, if any, disadvantages compared to MMRM or models that assume proportional treatment effects. While the categorical-time MMRM is virtually assumption-free with regard to the temporal mean trend, the framework cannot accommodate delays in study visits which makes it incompatible in practice with intention to treat analyses. The natural cubic spline model does make assumptions about the temporal mean trend, but these assumptions seem to reasonably capture group trends. Adding cognitive test version effects to the spline model results in very similar estimates as MMRM. Furthermore, imposing the spline assumptions allows data from delayed visits to be naturally incorporated, improves power relative to MMRM, and maintains Type I error control. In contrast, the proportional treatment effect assumption is too strong and has been violated in at least two AD trials. The proportional treatment effect models are also challenging to fit and exhibit unacceptable Type I error.

7 |. DATA AVAILABILITY STATEMENT

The ADNI data that support the PAD simulations are available from adni.loni.usc.edu. The MCI trial data are available from https://www.adcs.org/data-sharing/. The AZD0530 and insulin trial data may be requested from biostat_request@atrihub.io.