Figure 9:

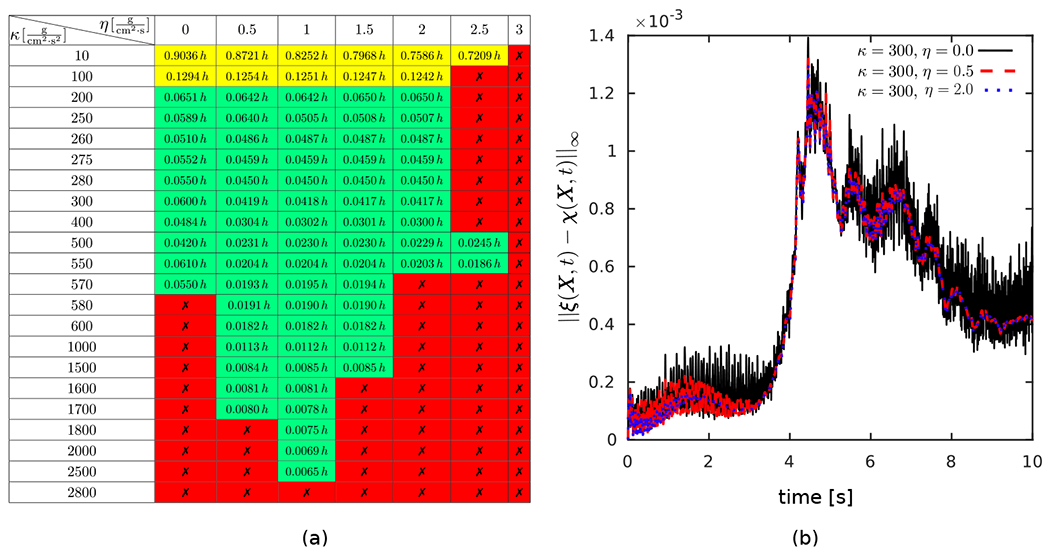
(a) A table of stable vs. unstable penalty pairs $(\kappa ,\eta )$ with red color cells marked by $\mathit{✖}$ symbol showing unstable cases. The numbers reported for stable pairs is the maximum discrepancy between the two Lagrangian representations $\parallel \mathit{\xi }(\mathit{X},t)-\mathit{\chi }(\mathit{X},t){\parallel }_{\mathrm{\infty }}$ at $t=10\mathrm{s}$, shown as a factor of $h\equiv h_{\mathrm{finest}.}$ Green cells are the acceptable cells with the additional condition of $\parallel \mathit{\xi }(\mathit{X},t)-\mathit{\chi }(\mathit{X},t){\parallel }_{\mathrm{\infty }}\le 0.1h_{\mathrm{finest}}$ imposed in our simulations. Yellow cells show stable cases with maximum discrepancy larger than $0.1h_{\mathrm{finest}.}$ A non-zero damping parameter does not seem to be required to achieve a stable result with an acceptable maximum discrepancy. Additionally, note that there can always be a small enough time-step for which the currently unstable pairs would become stable. (b) The maximum discrepancy between the two Lagrangian representations over time for 3 cases from the table with fixed $\kappa =300$ and different choices of $\eta$. Although the oscillations are all smaller than $0.1\mathrm{h}$, a small amount of non-zero damping is shown to further reduce spurious numerical oscillations.