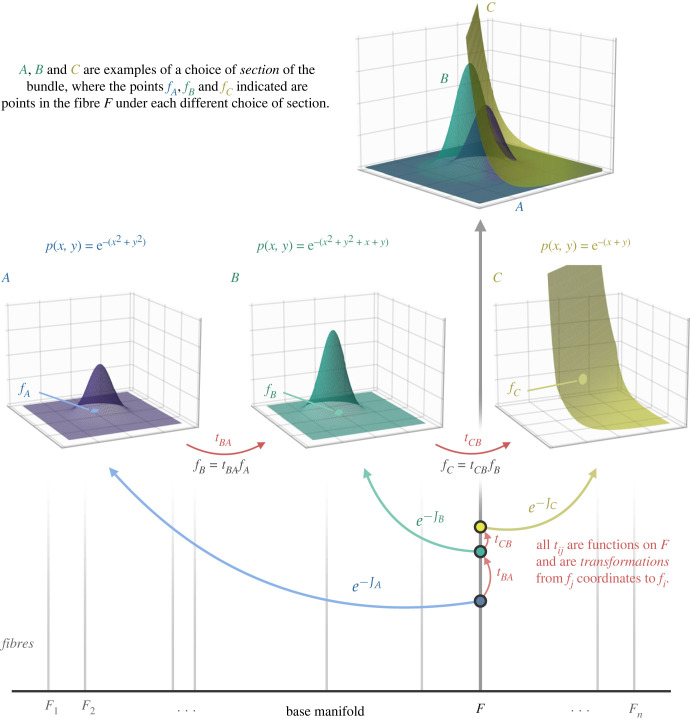
Figure 4.

Illustration of fibre bundles, sections and transformations. A fibre bundle exists on a base manifold, situated over points in that space. Here, the fibre is a copy of the real line attached to each point in the base. Different choices of section of the bundle correspond to different choices of constraint function. The section is a function which assigns coordinates in ‘probability space’—by which we mean values of probability, or specific points in the fibre F over some base point (x, y)—to points on the base. For f_A, f_B, f_C ∈ F, these points lie over the base point (x, y). The height of any f_i(x, y) corresponds to the probability of (x, y), and is a lift of (x, y) within the section p. Three simple choices of section are shown, with the same point (x, y) mapping to different regions of the corresponding probability density due to a different choice of constraint function (A, B and C). The inset over F shows that all of these densities are sections over the same base space.