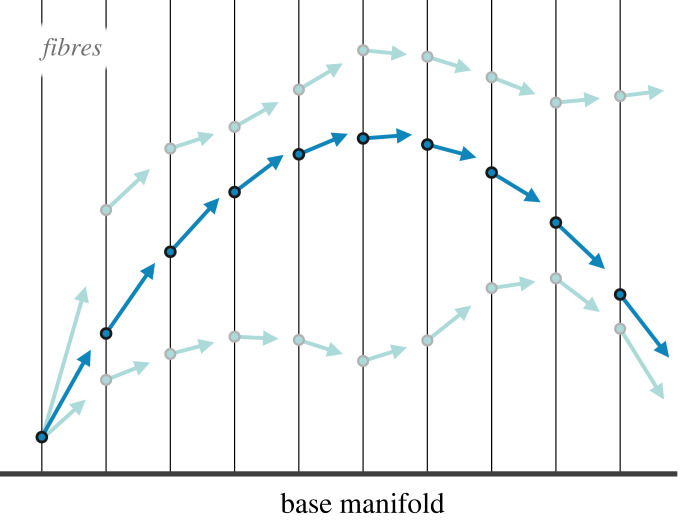
Figure 5.
Vector field on a curve. A connection in a bundle allows us to define a tangent vector field along a curve. Here, the constraints applied are directly constraints on the shape of such a curve, applied as a vector field constraining the motion of some particle to lie in the gradient of a potential. This particular path is curved, corresponding to a least action path—a geodesic with respect to some (curved) connection. In this local patch, we can also easily construct a flat connection with flat paths. We refer to paths that are flat as horizontal lifts, and parallel transport of points happens along these paths in particular.