Substrate binding in the allosteric site mimics homotropic cooperativity in the SIS‐fold glucosamine‐6‐phosphate deaminases

Abstract

Glucosamine‐6‐phosphate (GlcN6P) deaminases from Escherichia coli (EcNagBI) and Shewanella denitrificans (SdNagBII) are special examples of what constitute nonhomologous isofunctional enzymes due to their convergence, not only in catalysis, but also in cooperativity and allosteric properties. Additionally, we found that the sigmoidal kinetics of SdNagBII cannot be explained by the existing models of homotropic activation. This study describes the regulatory mechanism of SdNagBII using enzyme kinetics, isothermal titration calorimetry (ITC), and X‐ray crystallography. ITC experiments revealed two different binding sites with distinctive thermodynamic signatures: a single binding site per monomer for the allosteric activator N‐acetylglucosamine 6‐phosphate (GlcNAc6P) and two binding sites per monomer for the transition‐state analog 2‐amino‐2‐deoxy‐D‐glucitol 6‐phosphate (GlcNol6P). Crystallographic data demonstrated the existence of an unusual allosteric site that can bind both GlcNAc6P and GlcNol6P, implying that the homotropic activation of this enzyme arises from the occupation of the allosteric site by the substrate. In this work we describe the presence of this novel allosteric site in the SIS‐fold deaminases, which is responsible for the homotropic and heterotropic activation of SdNagBII by GlcN6P and GlcNAc6P, respectively. This study unveils an original mechanism to generate a high degree of homotropic activation in SdNagBII, mimicking the allosteric and cooperative properties of hexameric EcNagBI but with a reduced number of subunits.

Short abstract

PDB Code(s): 8EOL, 8EYM, 8FDB, 3HBA, 2VF5, 6SVP, 2ZJ4, and 1MOS

1. INTRODUCTION

GlcN6P deaminase (EC 3.5.99.6, NagB) catalyzes the isomerization‐deamination of glucosamine‐6‐phosphate (GlcN6P), releasing fructose‐6‐phosphate (Fru6P) and ammonium ion (NH₄ ⁺). This enzyme plays an essential role in amino‐sugar catabolism and, in some species, provides an important regulatory step as it displays positive cooperativity by its substrate, and allosteric activation by N‐acetylglucosamine‐6‐phosphate (GlcNAc6P). Allostery is the phenomenon by which ligand binding to one site regulates the properties of distant sites. If the affected property (either binding or catalysis) depends on the same ligand or substrate, it is referred to as homotropic allosteric regulation. If the ligand binding regulates the affinity for a different ligand or substrate it is referred to as heterotropic allosteric regulation. Positive cooperativity is observed if the regulated functional properties are enhanced, and negative cooperativity if the regulated functional properties are reduced. No cooperativity is present without allostery, either homotropic or heterotropic.

In Escherichia coli, NagB is a homohexamer, with a Rossmann‐like fold (Oliva et al., 1995), usually referred to as EcNagBI. On the other hand, NagB from the bacterium Shewanella oneidensis (Yang et al., 2006) and the archaeon Thermococcus kodakaraensis (Tanaka et al., 2005) present an entirely different fold based on the sugar isomerase (SIS) domain. This fold is found in several proteins that have a role in phosphosugar isomerization, like glutamine‐fructose‐6‐phosphate aminotransferase (GlmS) (Bateman, 1999). In S. oneidensis, the SIS‐analogous form of NagB‐I was designated NagB‐II (SoNagBII), and it also displays positive cooperativity and allosteric activation by GlcNAc6P, representing an unusual case of homoplasy since the convergence is not only in its catalytic function, but also in its allosteric regulation and cooperativity (Yang et al., 2006).

NagB‐II of Shewanella denitrificans (SdNagBII) has been previously crystallized, and its structure resolved (PDB 3HBA). SoNagBII and SdNagBII enzymes have been cloned and purified by our group, and we found that they share similar kinetic behavior. The kinetics of EcNagBI can be well described by the MWC model (Bustos‐Jaimes and Calcagno, 2001), in which two quaternary conformations with different catalytic properties are in equilibrium, and this equilibrium can be shifted either by the substrate (homotropic activation) or by the allosteric activator (heterotropic activation). In contrast, kinetic data for NagB‐II enzymes cannot be described by the MWC model. Fitting kinetic data of NagB‐II enzymes to Hill equation revealed that the degree of substrate cooperativity is too high for a dimer (n _H ≥ 2), revealing the existence of a previously unknown mechanism of cooperativity.

In this research, the kinetic behavior of SdNagBII has been analyzed in the light of isothermal titration calorimetry (ITC) curves for both the substrate and the allosteric activator and complemented with crystallographic data, revealing the location of a previously unknown allosteric site and unveiling the nature of the observed high homotropic cooperativity in this protein.

2. RESULTS

2.1. SdNagBII kinetics

Ligand‐free kinetic data for the NagBII enzymes from S. denitrificans and S. oneidensis were fitted to the Hill equation (Equation 1),

$$v_0=\frac{V_{\max }{\left[\mathrm{S}\right]}^{n_{\mathrm{H}}}}{K_{0.5}^{n_{\mathrm{H}}}+{\left[\mathrm{S}\right]}^{n_{\mathrm{H}}}},$$ (1)

where n _H is the Hill coefficient and K _0.5 is the concentration of substrate to reach half of the maximum velocity (V _max), and [S] is the substrate concentration. Kinetic characterization of SdNagBII revealed a sigmoidal curve in the absence of GlcNAc6P and a mixed V/K activation pattern by this activator, with a clear decrease in K _0.5 from 4.2 to 1.2 mM and a small increase in V _max from 46.5 to 53.4 μM/min (Figure 1a). Hill coefficient (n _H) in the absence of an activator is 1.82 ± 0.14 for SdNagBII (Table 1), which in practice is the same value as the maximum theoretical cooperativity for a dimeric enzyme (n _H = 2.0) (Kegeles, 1979). Moreover, n _H for SoNagBII is 2.51 ± 0.23 (Table 1 and Figure S1), considerably higher than its maximum theoretical value and is a violation of the mass‐action kinetics foundation of the Hill equation for a dimeric enzyme with two binding sites for the substrate. In contrast, EcNagBI shows homotropic activation with a n _H of 2.9, although it has six active sites (Bustos‐Jaimes et al., 2005). Thus, an n _H at or near 2 suggests that, in addition to the active‐site cooperativity, the substrate must be playing a second role in the observed homotropic activation of the enzyme.

FIGURE 1.

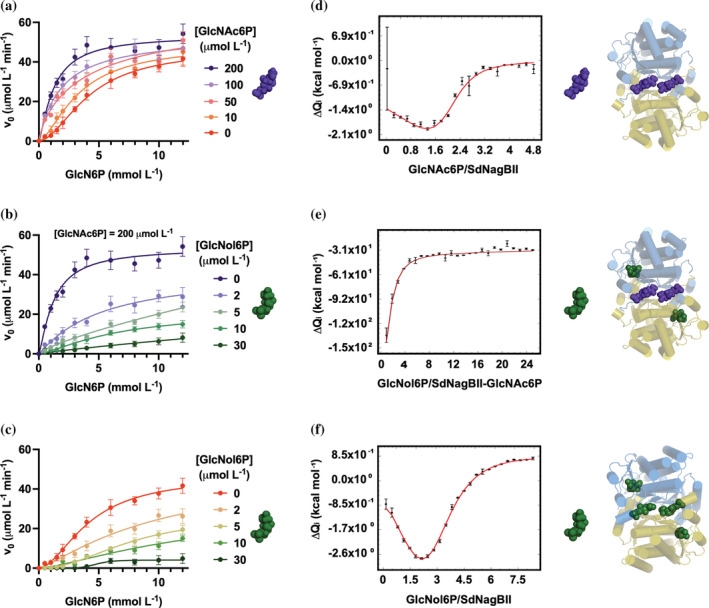
Kinetic characterization and ligand binding by SdNagBII. (a) Initial rate versus GlcN6P concentration at different fixed concentrations of the activator GlcNAc6P. (b) Initial rate versus GlcN6P concentration at different fixed concentrations of the inhibitor GlcNol6P in the presence of 200 μM of the activator GlcNAc6P. (c) Initial rate versus GlcN6P concentration at different fixed concentrations of the inhibitor GlcNol6P. Kinetic data are mean of three independent experiments and error bars represent standard deviation from the mean. (d) Binding isotherm obtained by integration of the raw data from titration of SdNagBII with consecutive injections of GlcNAc6P. Global fitting parameter χ ² = 2.6. (e) Binding isotherm obtained by integration of the raw data from titration of the GlcNAc6P‐saturated SdNagBII with consecutive injections of GlcNol6P. Global fitting parameter χ ² = 6.1. (f) Binding isotherm obtained by integration of the raw data from titration of SdNagBII with consecutive injections of GlcNol6P. Global fitting parameter χ ² = 4.1. GlcNAc6P and GlcNol6P are represented by the purple and green molecules. Cartoons next to the binding isotherms illustrate the ligand‐saturated species. Binding isotherms are mean of three independent experiments and error bars are the standard error of mean. Representative thermograms are given in Figure S4.

TABLE 1.

Kinetic parameters for SdNagBII and SoNagBII without allosteric effector.

Enzyme	k cat (s−1)	K 0.5 (mM)	n h
SdNagBII	7.74 ± 0.38	4.23 ± 0.32	1.82 ± 0.14
SoNagBII	6.02 ± 0.25	4.53 ± 0.23	2.51 ± 0.23

Note: Parameters obtained by fitting data of v ₀ versus [GlcN6P] in the absence of ligands to Equation (1). Data for SdNagBII are from Figure 1a and for SoNagBII from Figure S1. Uncertainties are the standard errors of the fitted parameters.

The allosteric activator, GlcNAc6P in concentrations up to 200 μM, increased V _max and reduced K _0.5, while higher concentrations did not have further activating effect. In the presence of 200 μM GlcNAc6P, SdNagBII kinetics curve becomes nearly hyperbolic (Figure 1b), and, in this condition, 2‐amino‐2‐deoxy‐D‐glucitol 6‐phosphate (GlcNol6P) becomes a classic competitive inhibitor with a competitive inhibition constant, K _I, of 0.391 ± 0.034 μM, and whose double reciprocal plot displays the typical pattern of this kind of inhibitor (Figure S2). GlcNol6P has been identified as a putative analog of the transition state for the isomerization and deamination of the substrate, GlcN6P (Oliva et al., 1995; Horjales et al., ¹⁹⁹⁹), thus this inhibition pattern is in agreement with GlcNol6P binding to the active site in the allosterically activated SdNagBII.

Kinetics of the hexameric EcNagBI can be explained by the MWC symmetry model, in which oligomeric enzymes exist in two quaternary structural states, designated R and T, with high and low activity, respectively. These structures are in an equilibrium that can be shifted to R by the substrate binding to the active site (homotropic activation) or allosteric activators (molecules different from the substrate binding to non‐catalytic sites). Equally, the R ↔ T equilibrium can be shifted to the low activity form of the enzyme (T state) by allosteric inhibitors, reducing the activity of the enzyme.

Additional support for the compliance of EcNagBI with the MWC model are the existence of two quaternary structures for the free and the ligated forms of the enzyme (Horjales et al., 1999), and the paradoxical activation produced by the dead‐end inhibitor GlcNol6P at low substrate concentrations (Bustos‐Jaimes et al., 2005), which, by binding to the enzyme, shifts the T to R equilibrium toward the high‐affinity R state producing this activation. In contrast, the inhibition pattern of SdNagBII with GlcNol6P did not produce the expected paradoxical activation at low substrate concentrations, though it remains an inhibitor (Figure 1c). Therefore, GlcNol6P does not follow the expected behavior for an active‐site competitive inhibitor in an enzyme following the MWC model.

The unexpected kinetics patterns of NagB‐II enzymes require an alternative explanation. It has been observed that the activity of some enzymes is modulated through changes in their oligomeric state in the so‐called morpheeins (Bouhaddou and Birtwistle, 2014; Selwood and Jaffe, ²⁰¹²). Moreover, the glucosamine‐6‐phosphate synthase (GlmS) dimer, an archetypical SIS‐fold enzyme, is in equilibrium with an inactive hexameric state in the presence of GlcN6P (Mouilleron et al., 2012). However, the analysis of the hydrodynamic radii of NagB‐II enzymes, studied by dynamic light scattering (DLS) and size exclusion chromatography (SEC) (Figure S3B,C) was consistent with the size of a dimer and did not change with either the substrate or the allosteric activator, making this mechanism of regulation unlikely for NagB‐II.

2.2. NagBII dimer has two binding sites for GlcNAc6P and four for GlcNol6P

Titration of SdNagBII with the allosteric activator, GlcNAc6P, by ITC showed a biphasic response (Figure 1d and Figure S4A), that was best fitted to a two‐site per dimer binding model. Thermal footprints of the binding sites for GlcNAc6P suggest that sites are analogous, and the small negative difference in the free energy change between steps [1] and [2] (ΔΔG_1‐2) (Table 2) indicates the absence of thermodynamic cooperativity.

TABLE 2.

Thermodynamic parameters from ITC analysis of SdNagBII for GlcNAc6P and GlcNol6P binding.

Reaction a	K d b (M)	ΔH c (cal mol−1)	ΔG d (cal mol−1)	TΔS e (cal mol−1)	ΔS f (cal mol−1 K−1)
Titration of SdNagBII with GlcNAc6P
[1] M2 + A ⟺ M2A1	(5.99 ± 0.59) E−07	(−1.36 ± 0.04) E+03	−8.41E+03	7.05 E+03	2.33 E+01
[2] M2A1 + A ⟺ M2A2	(5.26 ± 0.27) E−06	(−2.88 ± 0.05) E+03	−7.32E+03	4.45 E+03	1.47 E+01
Titration of GlcNAc6P‐saturated SdNagBII with GlcNol6P
[3] MA + L ⟺ MAL	(1.54 ± 0.17) E−04	(−2.71 ± 0.08) E+02	−5.29 E+03	5.02 E+03	1.66 E+01
Titration of SdNagBII with GlcNol6P
[4] M2 + L ⟺ M2L1	(5.99 ± 0.30) E−09	(−6.44 ± 1.19) E+03	−1.14 E+04	4.96 E+03	1.64 E+01
[5] M2L1 + L ⟺ M2L2	(7.19 ± 0.36) E−07	(7.14 ± 1.20) E+03	−8.52 E+03	1.57 E+04	5.17 E+01
[6] M2L2 + L ⟺ M2L3	(1.63 ± 0.38) E−05	(−1.41 ± 0.01) E+04	−6.64 E+03	−7.47 E+03	−2.46 E+01
[7] M2L3 + L ⟺ M2L4	(2.32 ± 0.62) E−03	(1.00 ± 0.00) E+05	−3.65 E+03	1.04 E+05	3.42 E+02

Note: Uncertainties are the standard errors of the fitted parameters. Thermograms in Figure S4 were used to obtain the fitting parameters, panel A for reactions [1] and [2], panel B for reaction [3], and panel C for reactions [4]–[7].

^a M₂ represents the dimer of SdNagBII, A represents GlcNAc6P, and L represents GlcNol6P.

^b Dissociation constant.

^c Association enthalpy change.

^d Gibbs free energy of association; calculated from K _d.

^e Calculated from ΔH and ΔG at T = 303.15 K.

^f Association entropy change; calculated from ΔS and T.

Next, the GlcNAc6P‐saturated enzyme was titrated with GlcNol6P to measure the stoichiometry for this ligand when GlcNAc6P occupies the allosteric site. ITC data revealed that the GlcNAc6P‐saturated dimer of SdNagBII binds two molecules of GlcNol6P in thermodynamically equivalent sites (Figure 1e and Figure S4B), step [3] in Table 2, as expected by homology with other proteins of the SIS‐fold family, in which a single binding site for GlcN6P is present per subunit (PDB codes 2VF5, 6SVP, 2ZJ4). It should be noted that these other SIS‐fold enzymes are not allosterically activated.

Subsequently, we studied the binding of GlcNol6P to SdNagBII in the absence of GlcNAc6P to determine its binding stoichiometry and to gain insight into the thermodynamic basis of the observed sigmoidal kinetics for this enzyme. The GlcNol6P binding isotherm is of a biphasic nature (Figure 1f and Figure S4C), and model fitting is consistent with four nonequivalent sites in the SdNagBII dimer. Thermodynamic parameters calculated from data fitted to the four‐site sequential binding model are shown in Table 2. The binding of GlcNol6P to the first and the third sites appear to be similar in their enthalpic components, while the second and fourth sites have enthalpic and entropic components sharing the same signs. Surprisingly, the difference in the free energy change between the different binding steps, ΔΔG_4‐5, ΔΔG_5‐6, and ΔΔG_6‐7, are negative, indicating a lack of positive cooperativity for this ligand again. Furthermore, negative values of ΔΔG_4‐5 and ΔΔG_6‐7 are totally enthalpy driven, as the measured enthalpy changes between binding steps [4] and [5] and binding steps [6] and [7] (ΔΔH_4‐5 and ΔΔH_6‐7) are negative. In contrast, the positive value of the change in the entropic component between binding steps [5] and [6], ΔTΔS _5‐6 (2.32E+04 cal mol⁻¹), reveals that the negative value of ΔΔG_5‐6 is strongly entropy driven and marks the third binding site as very different from the second one. Remarkably, these results imply a total heterogeneity among the four sites and show no positive cooperativity.

2.3. Insights from SdNagBII structure

The SdNagBII crystallized in two different space groups, C222₁ in the presence of GlcNol6P and P2₁2₁2₁ for the GlcNol6P‐GlcNAc6P complex and in the absence of ligands (APO) (Table 3). Two protein molecules were found in the asymmetric unit for all the structures, corresponding to a Matthews coefficient of 2.31 ų/Da and 46.8.% solvent for the GlcNol6P, 1.79 ų/Da, and 31.2% solvent for the GlcNol6P‐GlcNAc6P, and 1.84 ų/Da and 33.1% solvent for the APO structure. Subsequent refinement in Phenix of the structures yielded R _work/R _free values of 0.205/0.254, 0.186/0.233, and 0.188/0.231 for the SdNagBII‐GlcNol6P, SdNagBII‐GlcNol6P‐GlcNAc6P, and APO models, respectively. Data collection and refinement statistics are summarized in Table 3. The three structures were deposited in the PDB with accession numbers 8EOL, 8FDB, and 8EYM, for the APO SdNagBII, SdNagBII‐GlcNol6P, and SdNagBII‐GlcNol6P‐GlcNAc6P complexes, respectively.

TABLE 3.

Data collection and refinement statistics.

	GlcNol6P	GlcNol6P‐ GlcNAc6P	APO
	PDB 8FDB	PDB 8EYM	PDB 8EOL
Data collection
Wavelength (Å)	1.54	1.54	1.54
Space group	C2221	P212121	P212121
Unit cell dimensions [a, b, c (Å)]	71.89, 113.14, 171.01 90, 90, 90	73.18, 80.24, 91.51 90, 90, 90	72.38, 78.75, 96.86 90, 90, 90
Resolution (Å)	34.95–3.06	39.75–2.31	41.25–2.17
Highest‐resolution shell (Å)	3.21–3.06	2.35–2.31	2.21–2.17
No. of observed reflections	92,757	99,953	348,200
No. of unique reflections	13,430	22,873	29,534
Completeness (%)	98.3 (99.4)	95.0 (84.1)	98.5 (91.3)
Redundancy	7.1 (4.0)	4.6 (2.6)	11.0 (5.9)
Rmerge (%)	0.165 (0.625)	0.064 (0.223)	0.058 (0.381)
CC1/2	0.794	0.945	0.931
⟨I/σ(I)⟩	9.8 (2.10)	36.1 (3.7)	47.0 (5.0)
Refinement
R work (%)	0.206	0.186	0.188
R free (%)	0.241	0.233	0.231
Average B factor (Å2)	37.0	38.0	36.0
Bond lengths (Å)	0.006	0.008	0.010
Bond angles (°)	0.806	1.056	1.025
Ramachandran statistics (%)
Favored	97.3	97.7	97.6
Allowed	2.7	2.3	2.4

The APO form of SdNagBII was solved at a resolution of 2.17 Å and shows two regions of the protein without electronic density: residues 49 to 53 and 242 to 253. These residues are part of the active site pocket, which is missing in this structure (Figure 2a). The overall structure is similar to the previously deposited 3HBA, with an average RMSD = 1.677 Å calculated with PyMOL on all atoms of the dimer. The structure also has high B factors in the regions close to the putative binding sites for substrate (Figure 2d).

FIGURE 2.

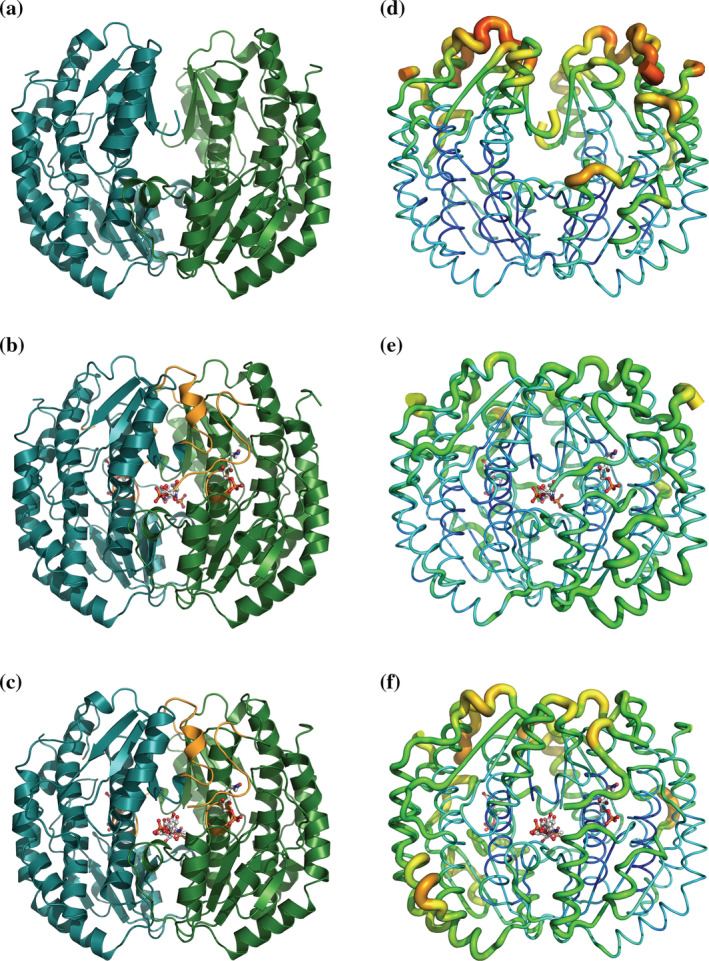
Dimeric structure of the APO form of SdNadBII (PDB 8EOL) (a), SdNadBII in complex with GlcNol6P (PDB 8FDB) (b), and SdNadBII in complex with GlcNol6P and GlcNAc6P (PDB 8EYM) (c). Unstructured regions in the APO form of the enzyme that are structured in the enzyme complexes are shown in orange in panels b and c. Thermal parameter (B‐factor) distribution in the APO form of SdNadBII (d), SdNadBII in complex with GlcNol6P (e), and SdNadBII in complex with GlcNol6P and GlcNAc6P (f). B factors are shown as “putty” representations, as implemented in PyMOL. The thicker coil lines show high B values.

The structure of SdNagBII in complex with GlcNol6P was solved at a resolution of 3.06 Å, and has four molecules of GlcNol6P bound per dimer. Two of these molecules are bound to the conserved active site pocket of the sugar isomerases family (Teplyakov et al., 2001) and their presence reduced the B factors in this region (Figure 2b,e); the other two molecules are bound to a novel site, not previously described for SIS‐fold proteins (Figure 3a). Contacts of GlcNol6P in the conserved active site are similar to those already observed in GFAT from E. coli (PDB 1MOS) (Teplyakov et al., 1999) (Figure 4). The active site is formed by residues that participate in the stabilization of the phosphate group, Ser52 and Ser97 from chain A. His243 from chain B is the one that opens the ring of the substrate, and we have confirmed its catalytic role by site‐directed mutagenesis by constructing the mutant His242Gln in SoNagBII, whose k _cat was ~1200‐fold lower than that of the wild type. Finally, Glu227 from chain A is the residue responsible for the enolization of the substrate, the last part of the catalytic mechanism. The conserved catalytic site is formed by residues in the area that do not show electronic density in the APO form of the enzyme, suggesting that it is very mobile and probably is only shaped when GlcNol6P binds in the novel site found.

FIGURE 3.

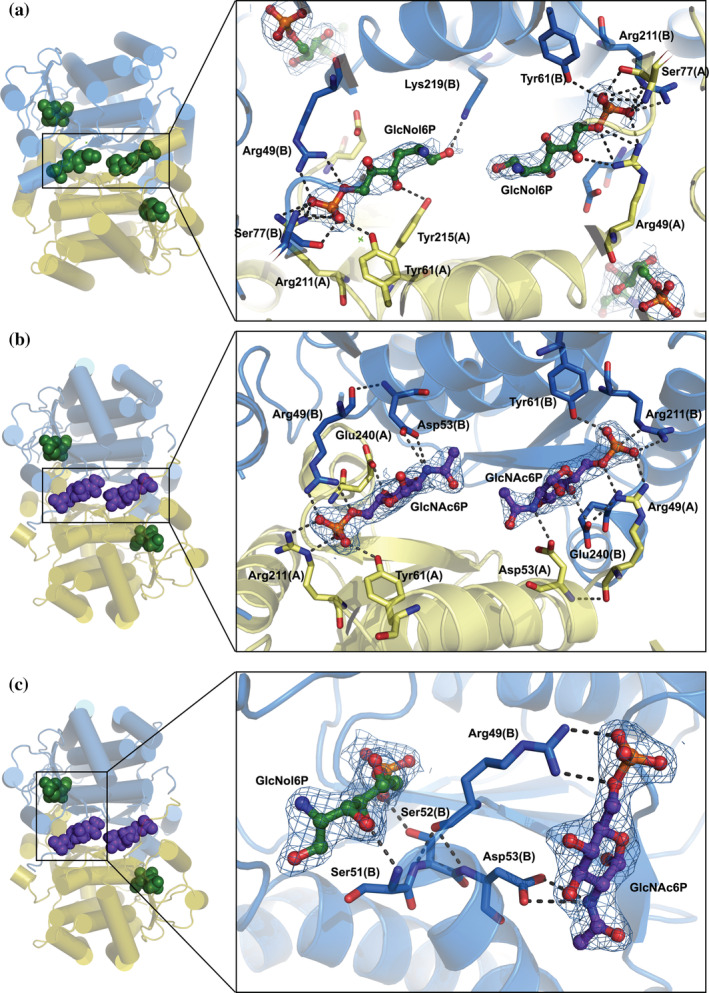
Structure of the novel allosteric site of SdNagBII. (a) The complex of SdNagBII with GlcNol6P (green) bound to both the active sites and novel allosteric site (with binding to allosteric site enlarged). (b) A complex of SdNagBII with GlcNol6P (green) at the active site and GlcNAc6P (purple) at the allosteric site (enlarged). Chains of the dimer are colored in blue and yellow, highlighting that the new allosteric site is at the interface between subunits. (c) Complex of SdNagBII with GlcNAc6P (purple) at the allosteric site and GlcNol6P (green) at the active site. Residues Arg49, Ser51, Ser52, and Asp53 communicate between the active and allosteric sites (enlarged); this segment (49–53) is unstructured in the APO form of the enzyme. For clarity, chain A is not shown in this projection. Polar interactions are indicated, and electron density maps 2Fo‐Fc contoured at 1 sigma are shown for the ligands.

FIGURE 4.

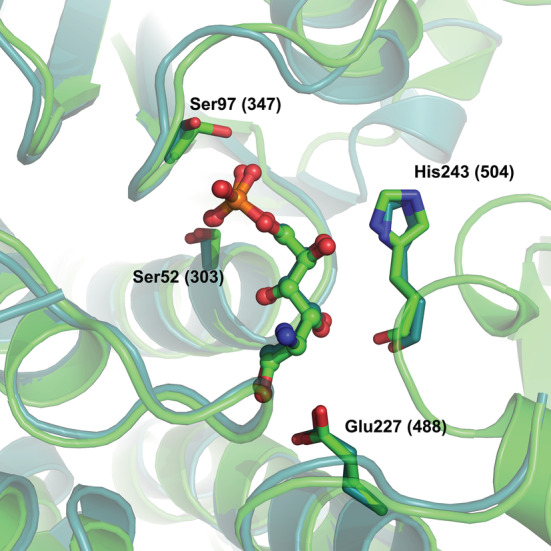
Superposition of the structures of the active sites of 1MOS (E. coli GFAT) (deep teal) and 8EOL (S. denitrificans NagB‐II) (green), showing a molecule of GlcNol6P bound to the active site pocket in both enzymes. Residues His243 (504), Ser52 (303), Ser97 (347), and Glu227 (488) are shown in stick representation, and GlcNol6P molecules are in ball and stick representation. The numbers in parentheses are for GFAT.

Amino acids of both subunits form the new allosteric sites, Arg49 from chain B and Arg211, Ser77, and Tyr61 from chain A directly bind the phospho‐group of GlcNol6P. Tyr215 in chain A and Lys219 from chain B complete the site (Figure 3a–c). Other polar contacts occur in the allosteric site and are listed in Table S1. Unexpectedly, the GlcNol6P molecule bound to the other novel site is not entirely symmetric with the first, having different H‐bonds with both enzyme subunits (Table 4 and Table S1).

TABLE 4.

Hydrogen bonds for GlcNol6P and GlcNAc6P with the allosteric site of SdNagBII.

GlcNol6P in chain A					GlcNol6P in chain B
GlcNol6P atom	Residue	Atom name	Chain	Distance (Å)	GlcNol6P atom	Residue	Atom name	Chain	Distance (Å)
O1P	Tyr61	OH	B	2.933	O1	Lys219	Nζ	B	3.030
O1P	Ser77	Oγ	A	2.582	O4	Tyr215	OH	A	2.929
O2P	Arg49	NH2	A	2.709	O1P	Tyr61	OH	A	2.708
O2P	Ser77	Nα	A	3.041	O1P	Ser77	Oγ	B	2.537
O2P	Arg211	NH2	B	3.168	O2P	Arg49	NH2	B	2.780
O3P	Ser237	Oγ	B	2.836	O2P	Ser77	Nα	B	2.921
					O2P	Arg211	NH1	A	2.822
					O2P	Arg211	NH2	A	3.057

GlcNAc6P in chain A					GlcNAc6P in chain B
GlcNAc6P atom	Residue	Atom name	Chain	Distance (Å)	GlcNAc6P atom	Residue	Atom name	Chain	Distance (Å)
N2	Asp53	N2	A	3.017	N2	Asp53	O δ1	B	3.349
O6	Arg49	NH1	A	3.049	O6	Arg49	NH1	B	3.065
O1P	Tyr61	OH	B	2.753	O1P	Tyr61	OH	A	2.645
O1P	Ser77	Oγ	A	2.698	O1P	Ser77	Oγ	B	2.754
O2P	Arg49	NH2	A	2.889	O2P	Arg49	NH2	B	2.768
O2P	Ser77	Nα	A	2.482	O2P	Ser77	Nα	B	2.728
O2P	Arg211	NH2	B	3.346	O2P	Arg211	NH2	A	2.912
O3P	Arg211	Nε	B	2.802	O3P	Arg211	Nε	A	2.789
O3P	Ser237	Oγ	B	2.676	O3P	Ser237	Oγ	A	2.699

The structure of the complex of SdNagBII with GlcNol6P and GlcNAc6P was solved at 2.31 Å. In this structure, the conserved active sites are occupied by GlcNol6P, and the novel allosteric sites found for GlcNol6P are bound by GlcNAc6P (Figure 3b). The active and allosteric sites are coupled through amino acid residues 49–53, which include Arg49 and Asp53 that directly interact with GlcNAc6P in the new allosteric site, and residues Ser51 and Ser52 that are bound to GlcNol6P in the active site (Figure 3c). Remarkably, as noticed for GlcNol6P, GlcNAc6P molecules bound at the allosteric sites are not located in fully symmetrical positions (Table 4 and Table S2). An unexpected feature of the GlcNAc6P occupation at the emergent site is that the acetyl groups do not participate in any direct contact with the enzyme, except through a water molecule with Lys219 and Tyr215 in chain A, but not in chain B. This feature may explain why GlcNol6P fits well in the same site and implies that the substrate, GlcN6P, can also occupy the same site.

The APO structure of SdNagBII crystallized in the same space group as the fully occupied enzyme, suggesting the absence of large quaternary changes. Likewise, superposition of APO and bound structures revealed that the heterotropic and homotropic activations of SdNagBII do not occur through changes in quaternary structure (average RMSD < 1.7 Å), although an expected small change in the compactness of the enzyme due to the induced fit is evident. Thus, the activation appears to be purely local as the occupation of the novel allosteric site reduces the mobility of the loop containing residues Ser51 and Ser52 in the active site pocket and consequently shapes it.

3. DISCUSSION

Cooperativity is widespread in cellular processes, especially in regulation of metabolism (Bush et al., 2012). According to Monod, the most interesting property of allosteric proteins is their capacity to mediate homotropic cooperative interactions between stereospecific ligands (Monod et al., 1965), which is the case we have found, even though they bind to nonequivalent sites. Despite the robustness of the classical models, the high complexity of living systems challenges any intuitive global interpretation (Monod, 1971). A wide spectrum of mechanisms has evolved to transmit information from one part of a molecule to another (Cui and Karplus, 2008), some of them have been discovered due to the development of high‐resolution methodologies or very accurate interpretations. Cárdenas, who found a unique mechanism of cooperativity (Cárdenas et al., 1978), remarked that the progress in studying regulatory mechanisms in enzymes depends on adequate technology and a guiding vision (Cárdenas, 2013). Present‐day applications of computational methods to biomolecular systems, combined with structural, thermodynamic, and kinetic studies, make possible a global approach to mechanisms of allosteric regulation and cooperativity (Cui and Karplus, 2008). Here, a novel mechanism for sigmoidal kinetics was unveiled through a combination of methods.

The kinetic study of SdNagBII showing sigmoidal curves suggested that, in the light of the classic models of cooperativity and the Hill's equation, it should be formed by more subunits than it has. Analysis of the hydrodynamic properties of SdNagBII and crystallographic results confirmed that it is a dimer and that its association state does not change with ligands.

In a dimeric enzyme, a Hill coefficient (n _H) = 2 implies that the equilibrium.

$$\mathrm{E}+\text{2L}\leftrightarrow {\mathrm{EL}}_2,$$

occurs in a single step, which implies the simultaneous interaction of the three molecules, a trimolecular reaction. Such reactions are uncommon because the probability of three molecules colliding at the same time, with the correct orientation, is very low (Weiss, 1997); instead, they occur through sequential binding with intermediaries:

$$\mathrm{E}+\text{2L}\leftrightarrow \mathrm{EL}+\mathrm{L}\leftrightarrow {\mathrm{EL}}_2.$$

A n _H > 2 implies that more than two substrate molecules are bound to catalytic sites, but SdNagBII has only two catalytic sites. The structural analysis of the enzyme bound to four molecules of GlcNol6P implies that the two new sites for this ligand reported here are not catalytic, as critical residues for catalysis are missing.

ITC analysis demonstrated the existence of two sites for the binding of GlcNAc6P, the allosteric activator of EcNagBI, displaying no positive cooperativity. Unexpectedly, the same technique implied the existence of four nonequivalent binding sites for the EcNagBI active‐site ligand GlcNol6P, and, surprisingly, they do not show the expected thermodynamic cooperativity. In contrast, when the enzyme is previously saturated with the allosteric activator, the titration curve of GlcNol6P revealed a stoichiometry of just two molecules of this ligand per dimer. Considering the chemical resemblance of GlcNol6P to GlcNAc6P, it is reasonable for the former to bind both the active and the allosteric sites. Therefore, structural analysis of the enzyme and its complexes with ligands was critical to have a complete image of the allosteric activation of NagB‐II enzymes.

The APO form of the SdNagBII protein confirmed the dimeric form of the protein and, more importantly, shows that the residues of the conserved catalytic site are in the region that does not show electronic density implying that it is unstructured in the absence of ligands. The structures with bound ligands show the existence of a novel site, different from the active site, that can bind both the allosteric activator and the competitive inhibitor. This site is not conserved in the sequence of other SIS domain proteins and does not exist in homologous proteins with a reported crystallographic structure. In addition, the analysis of sequences and phylogeny indicates that it is specific to some bacterial species (Yang et al., 2006; Rodionov et al., ²⁰¹⁰; Boulanger et al., ²⁰¹⁰). For this reason, we propose that the activator binding site is an emergent site in the SIS‐fold family evolution, with a critical role in the allosteric activation of the enzyme and the mimicry of the homotropic cooperativity by the substrate. The structural analysis revealed that the emergent site does not have any residue for opening the substrate ring, implying that it is not catalytic as spontaneous ring‐opening of GlcN6P is very slow (Montero‐Morán et al., 2001). No obvious quaternary changes occur because of ligand binding, but clear changes in temperature factors are noted. As shown in Table 3, the temperature factors are very similar among structures (average B‐factor: 37 Ų with GlcNol6P, 38 Ų with both ligands [GlcNAc6P and GlcNol6P], and 36 Ų in the protein without ligands). There is little flexibility in the polypeptide chains, both in the enzyme in complex with ligands and alone, as shown in Figure 2. Notably, however, there is more flexibility in the loops shown in Figure 2d without ligands. In contrast, the region that does not show electronic density in the APO form, residues 50–54 and 243–254, is structured in the ligated forms of the enzyme, and the active‐site surroundings show lower B factors (Figure 2d–f).

The observed binding of GlcNol6P to both the active and allosteric sites suggests that the substrate, GlcN6P, binds both sites too. We propose substrate binding to the allosteric site shapes the active site, as crystallography suggests. In that case, as the active site does not exist or its affinity is too low, the first substrate molecule will bind to the emergent allosteric site, enabling the contiguous active site to bind a second substrate molecule which will be an actual substrate for catalysis, thus producing the observed sigmoidal kinetics. The origin of the high cooperativity in NagB‐II enzymes can be understood through the mass action analysis of substrate binding to the enzyme, as shown in Scheme 1. The rate equation (Equation 2) derived from this mechanism (see Rate equation in Supporting Information S1), postulates that the occupation of each allosteric site enables the binding of the substrate in its corresponding active site and that no other interactions between active sites occur, is

$$v_0=\frac{V_{\max }\left(\frac{{\left[\mathrm{S}\right]}^2}{K_{\mathrm{S}1}}+2\frac{{\left[\mathrm{S}\right]}^3}{K_{\mathrm{S}1}{K}_{\mathrm{A}2}}+\frac{{\left[\mathrm{S}\right]}^4}{K_{\mathrm{S}1}{K}_{\mathrm{A}2}{K}_{\mathrm{S}2}}\right)}{K_{\mathrm{A}1}+\left[\mathrm{S}\right]+\frac{{\left[\mathrm{S}\right]}^2}{K_{\mathrm{S}1}}+\frac{{\left[\mathrm{S}\right]}^3}{K_{\mathrm{S}1}{K}_{\mathrm{A}2}}+\frac{{\left[\mathrm{S}\right]}^4}{K_{\mathrm{S}1}{K}_{\mathrm{A}2}{K}_{\mathrm{S}2}}},$$ (2)

where v ₀ is the initial rate, V _max is the maximal velocity, K _A1 and K _A2 are the macroscopic dissociation constants for the first and the second allosteric sites, and K _S1 and K _S2 are the macroscopic dissociation constants for the first and the second active sites. This expression resembles the Adair equation for oxygen saturation of hemoglobin (Adair et al., 1925). Here, as the active sites are not formed before the allosteric site is occupied, it is possible for the first site to be occupied despite having a lower affinity than the following site (K _A1 > K _S1 and K _A2 > K _S2), which is a severe limitation of the Adair equation to explain cooperativity as this equation requires that sites with lower affinities become occupied before sites with higher affinities (Bustos‐Jaimes et al., 2008). Equation (2), under the assumption of K _A1 > K _S1, K _A2 > K _A1, and K _A2 > K _S2, can undoubtedly produce high sigmoidicity as the substrate is raised at the fourth power, despite having only two genuine active sites in this enzyme. However, identical binding sites usually have indistinguishable dissociation constants for a ligand, which raises the question of how is K _A2 > K _A1? This is, however, in agreement with the crystallographic analysis for SdNagBII, where the allosteric sites are not symmetrical, either because of a preexisting asymmetry in the enzyme, or because the asymmetry is a consequence of steric hindrance between close sites generated upon ligand binding. Fitting kinetic data of SdNagBII to this equation reproduces this observed behavior well (Figure 5). Although Equation (2) is too parametrized for data fitting, it illustrates that a high degree of cooperativity can be produced with only two active sites.

SCHEME 1.

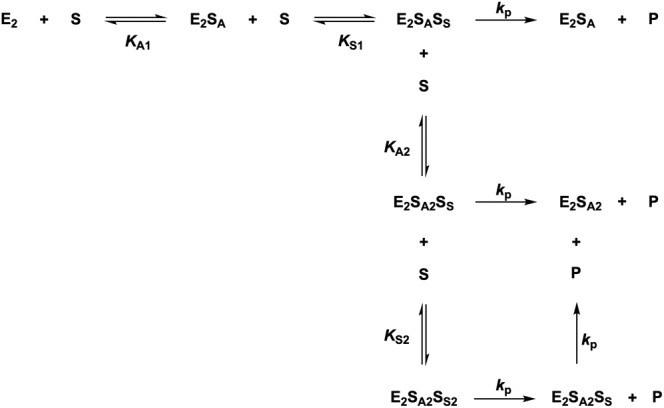
Equilibrium forms of the dimeric NagB‐II enzyme considering that the substrate (S) binds to the allosteric site (E₂S_A) and that only in this situation will the active site form and allow S to bind at the active site (E₂S_AS_S). Other complexes not contributing to the mass distribution of the enzyme are not shown, that is, E₂S_S, E₂S_S2, and E₂S_AS_S2. The value of k _p is considered identical among complexes for simplicity, though variations are possible.

FIGURE 5.

Experimental kinetic data of SdNagBII in the absence of GlcNAc6P at 30°C, pH 7.0, fitted to Equation (2). Experimental data are the same for 0 μM GlcNAc6P in Figure 1a,c. V _max was fixed to 46.48 μM/min corresponding to the V _max value from fitting the same data to Equation (1).

Considering the critical role of cooperativity in the regulation of metabolism, the convergence of NagB‐II enzymes to mimic this cooperativity through a completely different mechanism implies a solid underlying reason to tightly control the concentration of GlcN6P in the cell. However, it can also be mentioned that not all NagBI enzymes are allosteric (Vincent et al., 2005; Álvarez‐Añorve et al., ²⁰¹⁶). Previous studies from our group have not found conditions where the absence of cooperativity was manifested by effects on growth of E. coli (Álvarez‐Añorve et al., 2016). However, conditions that lead to a rapid change in the GlcN6P pool, thus requiring an instantaneous allosteric response, could exist considering the vast complexity of environmental components that bacteria might face. It is also possible that the strict regulation of GlcN6P concentration depends on the potential toxicity of this substrate. GlcN6P is a reducing amino sugar that is prone to undergo the Maillard reaction pathways, in whose first step the reducing group of the amino sugar reacts with amino groups of other substrate molecules or free amino groups from any protein to form Schiff bases, Amadori products and advanced glycation end‐products (AGEs). AGEs are terminal adducts irreversibly linked to proteins or DNA that affect their functions and, finally, are detrimental to cell viability (Henning and Glomb, 2016; Hrynets et al., ²⁰¹⁵). Maillard reactions are central to the theory of aging, and glycation of long‐lasting proteins is used as a general biomarker in aging research (Verzijl et al., 2000), and even bacteria such as E. coli are not exempt from AGEs accumulation (Mironova et al., 2001, 2003). Conversely, GlcN6P is also essential for the synthesis of UDP‐N‐acetylglucosamine, the precursor of peptidoglycan and lipopolysaccharide for cell‐wall construction (Johnson et al., 2013), and consequently its presence in growing bacteria is mandatory. With this in mind, for an optimal growth cycle, when GlcN6P concentration is low, sigmoidal kinetics would serve to avoid a substrate depletion that would reduce bacterial growth; on the contrary, when the GlcN6P concentration is high, the strong allosteric activation would prevent this substrate from exceeding its toxic threshold and lead to a harmful accumulation of AGEs.

4. CONCLUSION

Herein, we unveiled the mechanism of the allosteric activation of NagB‐II enzymes, which relies on the evolutive emergence of a novel binding site in these members of the SIS‐fold domain family. In contrast to enzymes following the MWC model like EcNagBI, NagB‐II enzymes exist in a single quaternary conformation, either ligated or not, showing only minimal changes attributable to the induced fit provoked by ligands bound to the enzyme. In this case, the observed homotropic activation occurs through the binding of a substrate molecule in the novel binding site, mimicking the homotropic activation but with an actual heterotropic origin as the activating substrate binds to a non‐active site. This tight regulation in some organisms can be justified because GlcN6P is an essential metabolite and at the same time a severe chemical threat.

5. MATERIALS AND METHODS

5.1. Expression and purification of NagBII enzymes

The nagB gene from S. denitrificans OS217 (GenBank ABE55984) was obtained by chemical synthesis (Epoch Bio Labs, Inc, USA) and cloned in the plasmid pET24b(+). The nagB gene from S. oneidensis MR‐1 (GenBank AAN56497, a kind gift from Valley Stewart, University California, Davis) was cloned in the pJES307 plasmid. The plasmids were used to transform E. coli strain BL21*∆nagEBACD pRARE cells (Álvarez‐Añorve et al., 2016). The transformed cells were grown in LB broth at 30°C and enzyme expression was induced with 1 mM IPTG for 3 h before harvesting. Cells were disrupted by mild sonication and the extract was centrifuged at 45,000 × g for 30 min. Native proteins were cloned and purified without use of tags. Both deaminases were purified by Source 15Q anion‐exchange preparative column equilibrated at pH 7.5 for SoNagBII and 8.5 for SdNagBII; they were eluted with a gradient of NaCl from 0 to 1 M prepared in 50 mM Tris–HCl buffer at the same pH. The reason to use a different pH is that SdNagBII is poorly soluble at pH 7.5.

We also used a Phenyl Sepharose preparative column equilibrated at their respective pH and eluting with a gradient of decreasing NaCl from 0.25 to 0 M. Purity of the enzyme was analyzed by SDS‐PAGE (Figure S3A). The absorptivity at 280 nm for the purified enzymes was calculated by the Edelhoch method (Edelhoch, 1967), and was used for protein quantification in the subsequent experimentation; the absorptivity value was 12,300 M⁻¹ cm⁻¹ for both enzymes. Stability at assay conditions was evaluated by Circular Dichroism on a Jasco J‐715 spectrophotometer, and by DLS on a Zetasizer μV (Malvern). DLS values for each sample were averaged over 10 runs of 10 measurements per run. Enzymes from both S. oneidensis and S. denitrificans were purified and characterized kinetically but as we were unable to produce usable crystals from the S. oneidensis enzyme we have reported detailed analysis only for SdNagBII. The two proteins are 85% identical (Figure S3D).

5.2. Kinetic properties

Kinetic studies were measured at 30°C in 50 mM Tris–HCl buffer at pH 7.5 for SoNagBII and 8.5 for SdNagBII with the concentrations of GlcN6P, GlcNol6P, and GlcNAc6P indicated in figures. We synthesized and purified GlcNol6P and GlcNAcP as previously reported (Leloir and Cardini, 1956). GlcN6P deaminase activity was measured by the amount of Fru6P formed at a fixed time using the previously described procedure (Calcagno et al., 1984). In short, the reactions components were mixed in glass test tubes in a final volume of 190 μL, and the reaction was started by the addition of 10 μL of 20 μM enzyme solution (100 nM finale) and immediately mixed by vortexing and then incubated at 30°C in a water bath for 15 min. The reaction was stopped by the addition of 2 mL of 10 M HCl. To quantify Fru6P, 0.5 mL of 0.1% resorcinol dissolved in 95% ethanol was added and then incubated in a water bath at 70°C for 10 min, and cooled at room temperature before absorbance readings were made at 512 nm. A standard curve of Fru6P with concentrations ranging from 0 to 0.5 mM was prepared and incubated in the same water bath at the same time as the reaction samples. The progress of the reaction was always kept below 5% conversion to measure initial reaction velocities. Data fitting and graph plotting were performed with Prism 5.0 for MacOS X (GraphPad Software Inc., USA). Nonlinear regression analyses were always checked by inspection of their residual plots. Errors given in tables and text are the standard errors of the fitted parameters. Results are the mean of at least three independent repetitions.

5.3. Oligomeric state

The oligomeric state was analyzed by molecular sieving in a calibrated Superdex S‐75 column equilibrated with buffer A (50 mM Tris–HCl, pH 8.0, 300 mM NaCl, 1 mM DTT). Samples of 1 mL of protein (0.2 mg/mL) in buffer A alone or with added ligand were loaded in the analytical column pre‐equilibrated in buffer A added with the corresponding ligand (0.3 mM). Additionally, we measured the hydrodynamic diameter by DLS of the proteins alone and complexed with their ligands at 30°C in a Zetasizer μV. Samples of protein (0.2 mg/mL) in buffer B (Tris–HCl 100 mM, pH 8.4, 300 mM NaCl, 1 mM DTT) were microfiltered through 0.22 μm polyvinylidene difluoride (PVDF) syringe filters (Millipore) before analysis. DLS values for each sample were averaged over 10 runs of 10 measurements per run (Figure S3B).

5.4. Site‐directed mutagenesis

Mutation H242Q in NagBII from S. oneidensis was designed using the Braman et al. method (Braman et al., 1996). PCR was performed using Pfu DNA polymerase (Altaenzymes) and the primers FH242Q 5′‐AGA GTT TCT CCA AGG TCC AGT GAC C‐3′, and RH242Q 5′‐GGT CAC TGG ACC TTG GAG AAA CTC T‐3′. The mutation was verified by sequencing using T7 promoter and T7 terminator primers.

5.5. Isothermal titration calorimetry

Titration of SdNagBII with GlcNol6P and GlcNAc6P was performed in a NanoITC (TA Instruments) at pH 8.5, 30°C. For the titration of SdNagBII with GlcNAc6P, 0.2 mL of 78 μM enzyme was titrated with 2 μL injections of 1.5 mM GlcNol6P. For the titration of GlcNAc6P‐saturated SdNagBII with GlcNol6P, 0.19 mL of 170 μM enzyme with 2 mM GlcNAc6P was titrated with 2 μL injections of 30 mM GlcNol6P. For the titration of SdNagBII with GlcNol6P, 0.3 mL of 34 μM enzyme was titrated with 2 μL injections of 3 mM GlcNol6P.

The model for GlcNAc6P binding is a sequential binding model:

$$\text{M2}+\mathrm{A}\leftrightarrow \mathrm{M}2\mathrm{A}+\mathrm{A}\leftrightarrow \mathrm{M}2\text{A2}.$$

The model for GlcNol6P binding to a GlcNAc6P‐saturated enzyme is a simple binding model:

$$\mathrm{MA}+\mathrm{L}\leftrightarrow \mathrm{MAL}.$$

The model for GlcNol6P is a sequential binding model:

$$\text{M2}+\mathrm{L}\leftrightarrow \mathrm{M}2\mathrm{L}+\mathrm{L}\leftrightarrow \mathrm{M}2\text{L2}+\mathrm{L}\leftrightarrow \mathrm{M}2\text{L3}+\mathrm{L}\leftrightarrow \mathrm{M}2\text{L4}.$$

The fitting parameters for each model were determined by minimizing the objective function χ ² as defined elsewhere (Piñeiro et al., 2019). The lower the χ ² value the better the fitting. Data fitting and graph plotting were performed in Affinimeter (https://www.affinimeter.com/). Affinimeter automatically treats raw data to generate the equilibrium isotherms as described by the authors of the program (Piñeiro et al., 2019). Results are the mean of at least three independent repetitions. The binding models were in agreement with the concurrent crystallographic results.

5.6. Crystallization of SdNagBII and SdNagBII complexes and X ray crystallography

Pure recombinant SdNagBII was crystallized using the sitting‐drop vapor diffusion method. We set initial crystallization conditions in 96‐well plates (Jena Bioscience, SWISSCI MRC 2), and four conditions gave suitable crystals using Crystal Screen I and II (Hampton Research). The best crystals grew in solution number 6 (0.2 M MgCl₂, 0.1 M Tris, pH 8.5, 30% (w/v) PEG 4000) of the Crystal Screen I. Optimization drops were set using the hanging drop method in 24 pool plates. Best crystals grew after 4–5 days of incubation at 18°C in 3 μL drops composed of equal volumes of a solution containing 15 mg/mL SdNagBII in 50 mM Tris–HCl, pH 8.5, with 1 mM 2‐amino‐2‐deoxi‐D‐glucitol 6‐phosphate (GlcNol6P) or 1 mM N‐acetyl‐D‐glucosamine 6‐phosphate (GlcNAc6P), and pool solution with 0.2 M MgCl₂, 0.25 M Tris–HCl pH 8.5, 30% (w/v) PEG 4000. Crystals containing both GlcNol6P and GlcNAc6P were grown in 1 mM GlcNAc6P and then soaked in the crystallization drop with 1 mM GlcNol6P 5 min before freezing for data collection. We determined the APO SdNagBII structure from crystals that grew in the presence of 1 mM GlcNAc6P; however, no density for the ligand was observed in the electron density maps.

5.7. Data collection and structure determination of SdNagBII and SdNagBII complexes

The crystallization tests, as well as the X‐ray diffraction data collection, and the construction of the structural models were carried out in LANEM‐IQ‐UNAM.

All the crystals were cryo‐protected with 35% glycerol and flash‐frozen in a nitrogen cryo stream at 100 K (Oxford Cryosystems). Complete datasets were collected using a rotating anode generator MicroMax 007HF (Cu Kα, λ = 1.5418 Å) with a DECTRIS‐PILATUS 3 R/200K‐A detector. Collection strategies, indexing, integration, and data scaling were achieved using the HKL‐3000 software (Minor et al., 2006).

Initial molecular replacement was obtained for the SdNagBII‐GlcNol6P complex using the CCP4‐on‐line Balbes program (Long et al., 2008); the GlcNol6P ligand was added using Coot, and the model was refined by several cycles of Coot and Phenix.refine (Emsley et al., 2010; Adams et al., ²⁰¹⁰). To obtain the APO SdNagBII, and SdNagBII‐GlcNol6P‐GlcNAc6P model complexes, the initial SdNagBII‐GlcNol6P model was used in Phaser‐MR (Phenix), and the ligands for all complexes were modeled using Coot and refined through several cycles of Coot and Phenix.refine. Data collection and refinement statistics are summarized in Table 3. Structural figures and images were created with PyMOL.

AUTHOR CONTRIBUTIONS

Jorge Marcos‐Viquez: Conceptualization (equal); formal analysis (equal); investigation (equal); writing – original draft (equal). Annia Rodríguez‐Hernández: Formal analysis (equal); investigation (supporting); methodology (supporting). Laura Iliana Álvarez‐Añorve: Investigation (equal). Andrea Medina‐García: Investigation (equal); methodology (equal). Jacqueline Plumbridge: Methodology (equal); resources (equal); writing – review and editing (equal). Mario Luis Calcagno: Conceptualization (equal); funding acquisition (equal); resources. Adela Rodríguez‐Romero: Formal analysis (equal); methodology (equal); resources; writing – review and editing. Ismael Bustos‐Jaimes: Conceptualization (lead); data curation (equal); project administration (lead); resources (lead); supervision (lead); writing – original draft (lead).

Supporting information

Data S1. Supporting Information.

Marcos‐Viquez J, Rodríguez‐Hernández A, Álvarez‐Añorve LI, Medina‐García A, Plumbridge J, Calcagno ML, et al. Substrate binding in the allosteric site mimics homotropic cooperativity in the SIS‐fold glucosamine‐6‐phosphate deaminases. Protein Science. 2023;32(6):e4651. 10.1002/pro.4651

DATA AVAILABILITY STATEMENT

Data is available on reasonable request from the authors.