Modeling Inelastic Responses Using Constrained Reactive Mixtures

Abstract

This study reviews the progression of our research, from modeling growth theories for cartilage tissue engineering, to the formulation of constrained reactive mixture theories to model inelastic responses in any solid material, such as theories for damage mechanics, viscoelasticity, plasticity, and elasto-plastic damage. In this framework, multiple solid generations $\alpha$ can co-exist at any given time in the mixture. The oldest generation is denoted by $\alpha =s$ and is called the master generation, whose reference configuration ${\mathbf{X}}^s$ is observable. The solid generations $\alpha$ are all constrained to share the same velocity ${\mathbf{v}}^s$, but may have distinct reference configurations ${\mathbf{X}}^{\alpha }$. An important element of this formulation is that the time-invariant mapping ${\mathbf{F}}^{\alpha s}=\partial {\mathbf{X}}^{\alpha }/\partial {\mathbf{X}}^s$ between these reference configurations is a function of state, whose mathematical formulation is postulated by constitutive assumption. Thus, reference configurations ${\mathbf{X}}^{\alpha }$ are not observable $(\alpha \ne s)$. This formulation employs only observable state variables, such as the deformation gradient ${\mathbf{F}}^s$ of the master generation and the referential mass concentrations ${\rho }_r^{\alpha }$ of each generation, in contrast to classical formulations of inelastic responses which rely on internal state variable theory, requiring evolution equations for those hidden variables. In constrained reactive mixtures, the evolution of the mass concentrations is governed by the axiom of mass balance, using constitutive models for the mass supply densities ${\hat{\rho }}_r^{\alpha }$. Classical and constrained reactive mixture approaches share considerable mathematical analogies, as they both introduce a multiplicative decomposition of the deformation gradient, also requiring evolution equations to track some of the state variables. However, they also differ at a fundamental level, since one adopts only observable state variables while the other introduces hidden state variables. In summary, this review presents an alternative foundational approach to the modeling of inelastic responses in solids, grounded in the classical framework of mixture theory.

1. Introduction

The objective of this study is to review the progression of our research, from modeling growth theories for cartilage tissue engineering, to the formulation of constrained reactive mixture theories to model inelastic responses in any solid material, such as theories for damage mechanics, viscoelasticity, plasticity, and elasto-plastic damage. Our initial motivation for formulating suitable biological tissue growth theories, using the framework of reactive mixture theory, confronted us with the need to account for the evolution of tissue composition over time, and the formulation of reference configurations for various growth generations of solid matrix constituents, such as the collagen matrix of articular cartilage. A theoretical framework that accounts for evolution of material composition, while also accounting for the reference configuration of sequential generations of solid constitutents, turns out to be quite versatile, not limited to the modeling of growth.

The experimental field of cartilage tissue engineering arguably started in the 1990s [29–31], with the goal of growing cartilage, first in vitro, then in vivo, to treat osteoarthritis in younger populations. Osteoarthritis is a pervasive degenerative disease that afflicts articular joints such as the hip, knee and shoulder [2]. A hallmark of osteoarthritis is wear and ablation of the articular cartilage layers that line these diarthrodial joints, providing the bearing surfaces that transmit large joint contact loads with reciprocal sliding motions, while producing low friction under normal conditions such as activities of daily living. In humans, the articular cartilage layer varies in thickness, averaging less than one millimeter in finger and thumb joints [42], but reaching up to six or seven millimeters in some of the articular layers of the knee joint [12] (Figure 1a). When cartilage has worn away completely, the underlying innervated subchondral bone becomes exposed (Figure 1b), and innervated soft tissues that surround the joint are subjected to abnormal loads and stretching, often leading to debilitating joint pain [62]

Figure 1:

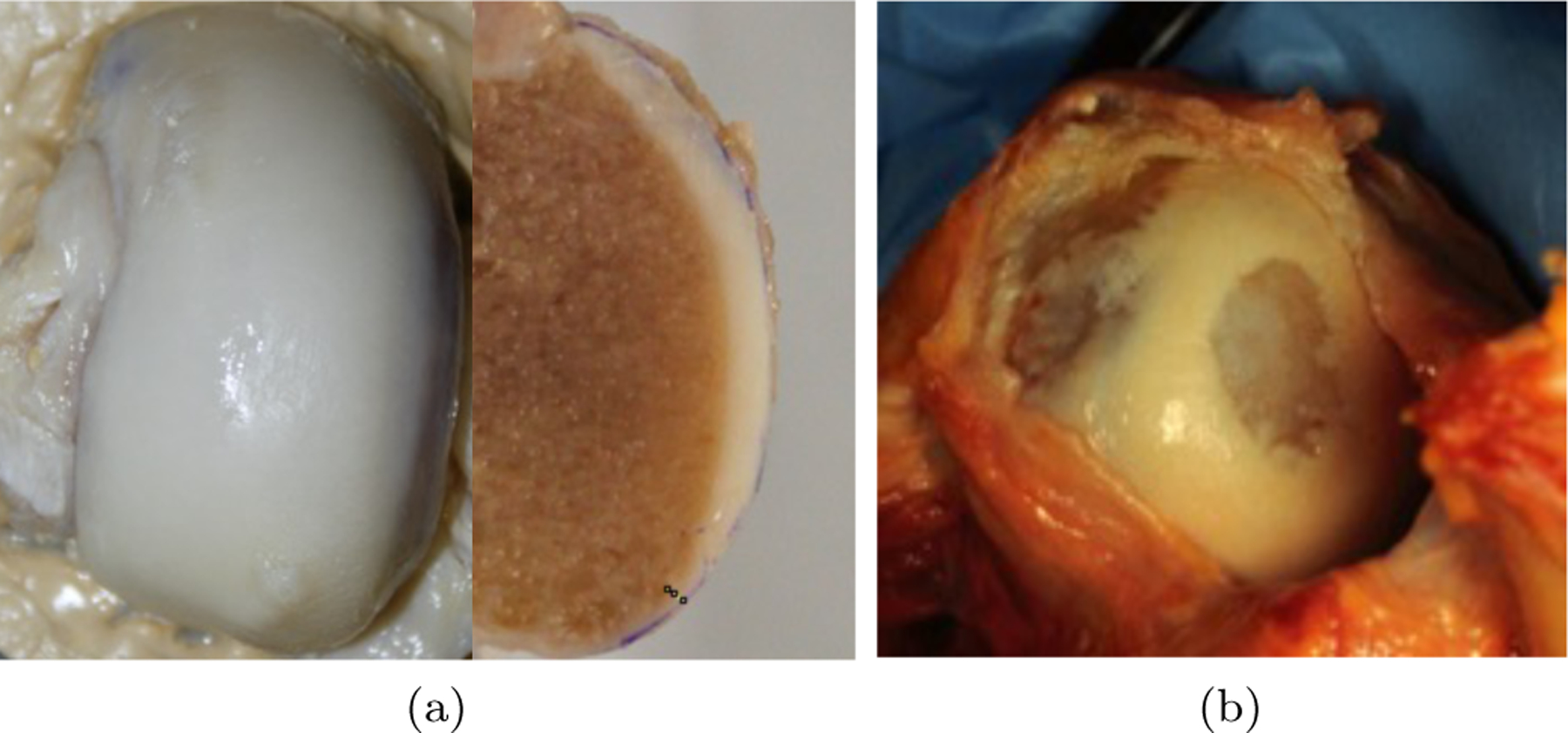
(a) Front and sectional side views of relatively healthy adult human femoral condyle (knee joint), showing articular cartilage as the white tissue covering the end of this long bone (vertical dimension ≈ 8 cm). (b) Osteoarthrtitic adult human humeral head (shoulder joint) cartilage looks more yellowish. In this image, cartilage has worn down to the bone at two locations. The radius of the humeral head articular surface is approximately 2.5 cm.

Since cartilage degeneration often evolves quietly until cartilage has completely worn away, most symptomatic patients present themselves to the clinic with significant cartilage loss, limiting treatment options considerably. The most common treatment for advanced osteoarthritis is total joint replacement, using metal and polyethelyne components [39]. This highly successful clinical procedure is often considered to be limited by the life expectancy of patients, relative to that of the artificial joint, since repeated surgical interventions are not favored in the elderly. Therefore, for younger patients, orthopaedic researchers have contemplated the alternative option of resurfacing degenerated joints using engineered tissues, such as engineered cartilage or osteochondral constructs, as a precursor to total joint replacement [43].

2. Cartilage Tissue Engineering

Our initial efforts in the experimental field of cartilage tissue engineering [52–54] led to the successful growth of small cylindrical cartilage tissue constructs (with a typical diameter of 6 mm and thickness of 2 mm). In these early studies, the dimensions of these constructs remained nearly unchanged over several weeks in culture (Figure 2a), whereas the constructs’ equilibrium compressive Young’s modulus (Figure 2b), and composition (principally, proteoglycan and collagen content, Figure 2c,d) increased significantly over time. These findings later motivated us to formulate an interstitial growth theory that depended on the evolution of tissue composition, as proposed by Cowin and Hegedus [27], in contrast to the classical growth theories of Skalak et al. [71] and Rodriguez et al. [67], which relied on the evolution of the tissue shape.

Figure 2:

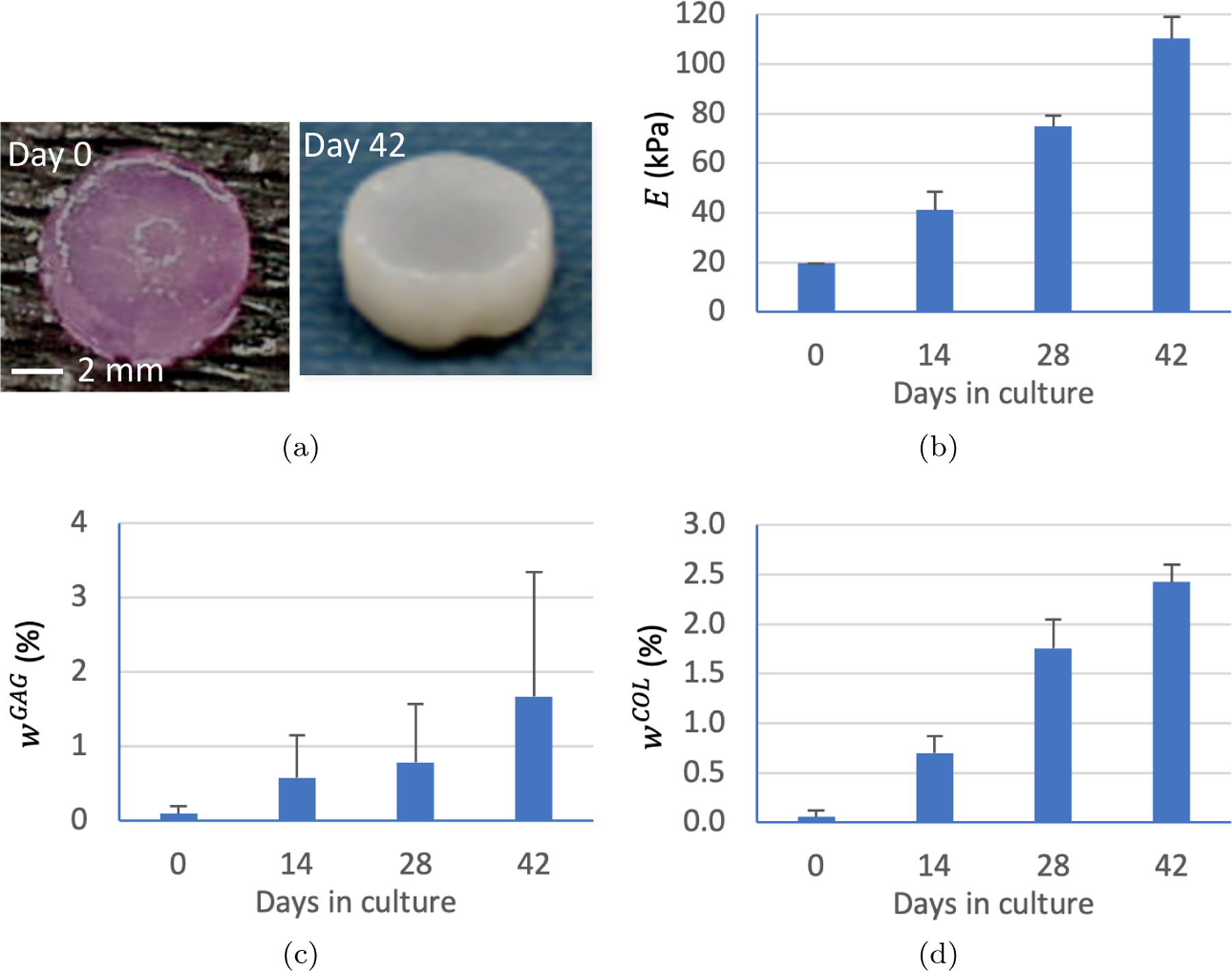
Cartilage tissue engineering results from the study of Mauck et al. [55]. (a) Constructs did not change significantly in size over 6 weeks in culture. (b) Equilibrium Young’s modulus, (c) mass fraction $w^{GAG}$ of proteoglycan content, and (d) mass fraction $w^{COL}$ of collagen content all increased significantly over time in culture. The mass fraction of interstitial fluid in these porous constructs can be deduced from $w^f\approx 1-w^{AG}-w^{GAG}-w^{COL}$, as collagens and proteoglycans make up the vast majority of solid matrix constituents in cartilage, and the mass fraction of the agarose scaffold, $w^{AG}\approx 0.02$, remained fixed over time in culture.

With further experimental investigations, we were able to increase the amount of tissue matrix deposition in culture by using higher cell seeding densities and larger supply of nutrients in the growth culture media used in our studies [55]. However, we also realized that nutrient consumption by cartilage cells located closer to construct boundaries immersed in culture media, significantly diminished the amount of nutrients available to cells located deeper in our tissue constructs [38]. We could make no further progress unless we added nutrient channels in our tissue constructs, as demonstrated preliminarily in small constructs in one of our earlier studies [16].

We were then confronted with the challenge of identifying the optimal placement of channels in larger constructs that would be suitable for resurfacing an entire articular layer in a diarthrodial joint. To meet this challenge, we formulated a growth theory that could account for the transport of nutrients from an external bath into the construct, the consumption of these nutrients by the cells, and the synthesis of matrix products by those cells. We used the framework of (unconstrained) reactive mixtures [4] based on the original mixture theory formulations of Truesdell [73, 74], Bowen [19], and others [15].

In this framework, the mixture may consist of solid constituents, including the scaffold material used in our tissue constructs (e.g., agarose), the fibrillar collagen and aggregating proteoglycans synthesized by cells, and other constituents such as crosslinks that form within, and stiffen, the collagen matrix; fluid constituents include the solvent (water) and the vast range of solutes present in growth culture media (salt ions, glucose, growth factors, etc.). The mixture is described as unconstrained because fluid constituents each have a velocity distinct from one another, and distinct from the solid matrix velocity. It is a reactive mixture since reactions occur, such as the consumption of interstitial fluid nutrients by cells, and the synthesis of solid matrix constituents by those cells,

$$\text{cells}+\text{nutrients}\to \text{cells}+\text{matrix products}$$ (1)

We implemented this growth theory [7, 9] into the open-source finite element code FEBio (febio.org) [48, 49], to identify optimal channel placement in large constructs. To inform these models, we first needed to experimentally characterize the essential nutrients in our growth media [22], the rate of consumption of these nutrients by the cells, and the rate of synthesis of matrix products by cells [59]. Using those measurements, we were then able to run computational simulations of constructs with various numbers of channels, helping us identify a theoretical optimal amount of nutrients and channels per construct [23, 60]. Then, we validated the results of these simulations with a final set of experiments [24, 25].

Armed with this information, we were finally able to engineer channeled constructs large enough that they could theoretically be used to resurface an entire articular joint [21] (Figure 3). At this juncture however, having increased cell seeding density and nutrient supply, and having provided a sufficient number of nutrient channels, we were now observing significant increases in the sizes of our tissue constructs (Figure 3), in contrast to our earliest studies (Figure 2a). This significant volumetric increase could be attributed to the large (supra-physiologic) deposition of negatively-charged proteoglycans by the cartilage cells, wherease the synthesis of collagen matrix, which normally restrains the swelling effect of proteoglycans, remained sub-physiologic [59]. Indeed, it is well known that negatively-charged proteoglycans attract cations from the surrounding bath into the tissue, at concentrations that increase the tissue osmolarity [50, 51, 75]. This osmolarity gradient drives solvent (water) from the bath into the tissue, producing a swelling pressure known as the Donnan osmotic pressure [46].

Figure 3:

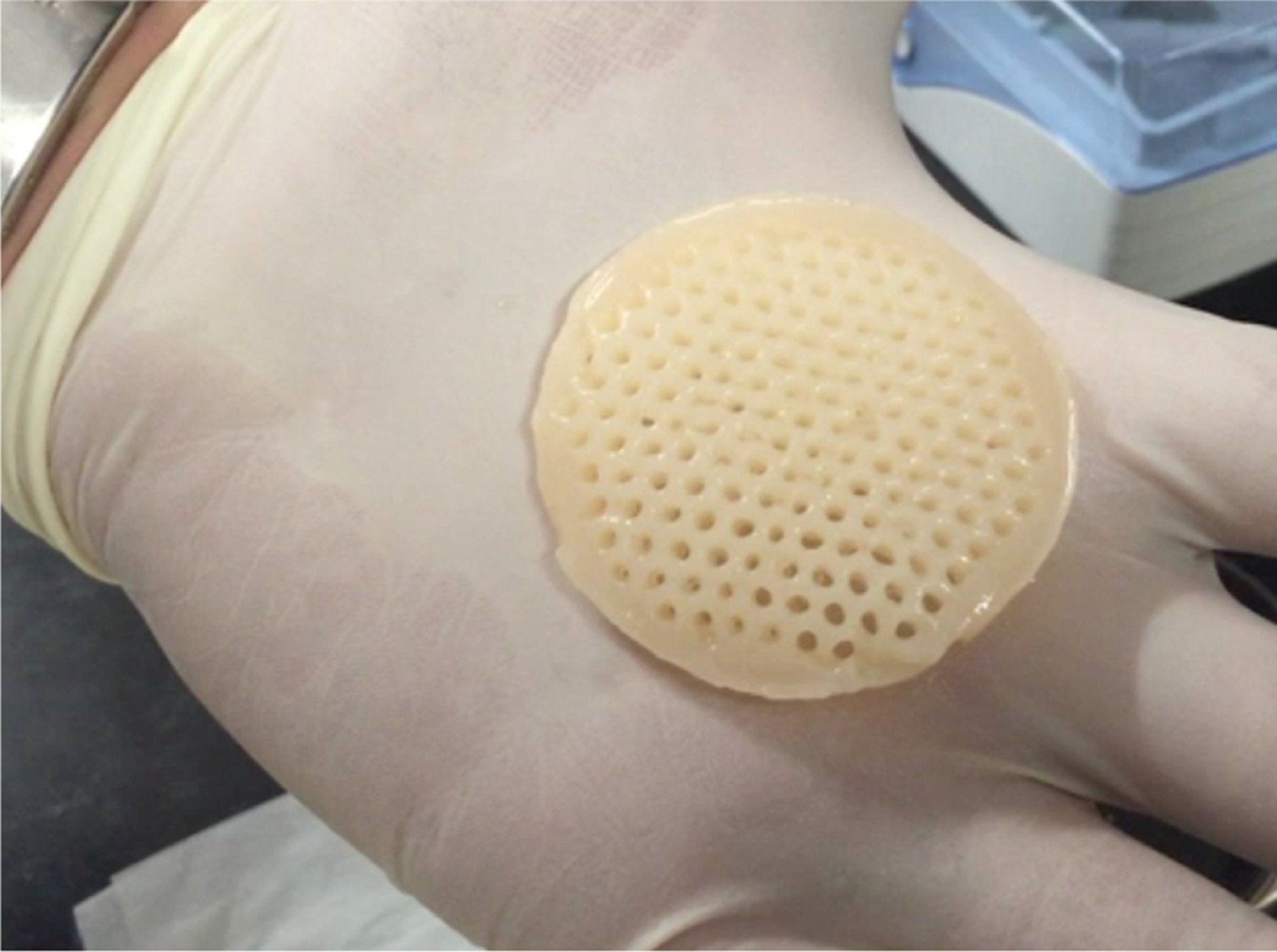
Engineered cartilage tissue construct from the study of Cigan et al. [21], after 56 days in culture. The holes served as nutrient channels during tissue culture. This construct grew from a diameter of 40 mm and thickness of 2.5 mm, to a diameter of 52 mm and a thickness of 4 mm by day 56. Its size was comparable to some of the largest articular layers in the human body.

This observation of significant tissue swelling over weeks in culture led us to the formulation of two important theoretical frameworks: (1) Since cells continuously produced collagen matrix over these weeks in culture, we surmised that the collagen deposited at different times in culture must have had different reference configurations, due to increased swelling over time. We called this phenomenon multigenerational growth and we proposed that each generation had a reference configuration that could be postulated by assumption [11]. In other words, we proposed that the reference configuration of each generation is a function of state that requires a constitutive relation. (2) As elaborated in the next paragraphs, we surmised that excessive swelling cause by proteoglycans could cause tissue damage, leading to our formulation of a damage theory in the context of mixtures [61].

The observed disparity in the rate of synthesis of proteoglycans and collagen was most likely due to the fact that cartilage cells (chondrocytes) used in our experimental tissue engineering studies were obtained from bovine calves, whereas cartilage normally undergoes its most significant growth process in utero, under very different biochemical conditions. In other words, the immature bovine chondrocytes used in our studies did not spontaneously recapitulate their in utero phenotype, thus synthesizing proteoglycans at a greater rate than collagen.

We became concerned that this differential growth rate could lead to damage of the fledgling collagen matrix due to excessive Donnan osmotic swelling pressure caused by the proteoglycans. If this damage were to occur, it would compromise the quality of our engineered tissue constructs, despite the fact that these constructs were produced de novo. To investigate this hypothesis, we needed to formulate a theoretical framework for damage mechanics, preferably consistent with our reactive mixture theory framework used to model growth, since we wanted to experimentally validate the presence of construct collagen damage using compositional measurements, based on biochemical assays [14].

In summary, we adapted Truesdell’s general theory of mixtures into a practical reactive mixture theory that could accommodate reactions between various solid and fluid constituents of a mixture [4], and implemented this framework computationally [7, 9]. We also formulated a multigenerational growth theory for the solid constituents of our tissue constructs [11], as well as a damage theory to account for excessive swelling [61], using mixture theory. For reactive processes taking place among solid matrix constituents, we adopted the assumption of Humphrey and Rajagopal [37], namely that solid constituents were all constrained to share the same velocity, even though each solid constituent could have a distinct reference configuration.

3. Reactive Mixtures

Our isothermal framework for unconstrained reactive mixtures was presented in [4]. The review presented in this article focuses on constrained reactive mixtures of solid constituents, following the definition of constrained mixtures presented by Humphrey and Rajagopal [37] and further elaborated upon by Wan et al. [77]. In a recent study [13], we developed the general formulation for such mixtures without restricting it to isothermal processes. Here, we summarize the salient features of this framework, though we limit the presentation to isothermal conditions.

3.1. Kinematics of a Constrained Mixture

Each solid constituent in a constrained reactive mixture is denoted generically by $\alpha$. The reference configuration of constituent $\alpha$ is represented by the referential position of material points ${\mathbf{X}}^{\alpha }$. Since solid constituents may come into existence at different times, we denote the oldest generation of all constituents by $\alpha =s$. We treat the reference configuration ${\mathbf{X}}^s$ of that oldest generation as being observable and we call it the master generation. For example, in cartilage tissue engineering, the oldest generation represents the tissue construct on the day of its initial manufacturing (day 0), when it consists only of agarose gel (the scaffold) and chondrocytes (cartilage cells) dispersed throughout that scaffold. The observable dimensions of the unloaded construct on day 0 represent the (presumably stress-free) configuration ${\mathbf{X}}^s$.

In mixture theory [15, 18], all constituents $\alpha$ present in the mixture at the current time $t$ satisfy

$$\mathbf{x}={\mathit{\chi }}^{\alpha }\left({\mathbf{X}}^{\alpha },t\right)={\mathit{\chi }}^s\left({\mathbf{X}}^s,t\right),$$ (2)

where $\mathbf{x}$ is the spatial position of the elemental mixture volume $dV$ through which all constituents $\alpha$ are passing at the current time $t$. In general, the initial position ${\mathbf{X}}^{\alpha }$ of material particle $\alpha$ is not the same for all constituents, which we may denote with ${\mathbf{X}}^{\alpha }\ne {\mathbf{X}}^s$. The velocity of constituent $\alpha$ is given by ${\mathbf{v}}^{\alpha }=\partial {\mathit{\chi }}^{\alpha }/\partial t$. However, in a constrained mixture, all constituents share the same velocity [37], thus we let ${\mathbf{v}}^{\alpha }={\mathbf{v}}^s$ for all $\alpha$,

$$\frac{\partial {\mathit{\chi }}^{\alpha }\left({\mathbf{X}}^{\alpha },t\right)}{\partial t}=\frac{\partial {\mathit{\chi }}^s\left({\mathbf{X}}^s,t\right)}{\partial t}.$$ (3)

Similarly, we define the deformation gradient of constituent $\alpha$ as ${\mathbf{F}}^{\alpha }=\partial {\mathit{\chi }}^{\alpha }/\partial {\mathbf{X}}^{\alpha }$. Using the chain rule of differentiation and the general relation of eq.(2), we may relate ${\mathbf{F}}^{\alpha }$ to the observable deformation gradient ${\mathbf{F}}^s$ of the master generation using

$${\mathbf{F}}^s=\frac{\partial {\mathit{\chi }}^s}{\partial {\mathbf{X}}^s}=\frac{\partial {\mathit{\chi }}^{\alpha }}{\partial {\mathbf{X}}^{\alpha }}\cdot \frac{\partial {\mathbf{X}}^{\alpha }}{\partial {\mathbf{X}}^s}={\mathbf{F}}^{\alpha }\cdot {\mathbf{F}}^{\alpha s},$$ (4)

where ${\mathbf{F}}^{\alpha s}=\partial {\mathbf{X}}^{\alpha }/\partial {\mathbf{X}}^s$ is a time-invariant mapping between the reference configurations ${\mathbf{X}}^{\alpha }$ and ${\mathbf{X}}^s$. As proposed in [11] and further clarified in [13, 81], ${\mathbf{F}}^{\alpha s}$ is a function of state which may be postulated by constitutive assumption, and constrained by the Clausius-Duhem inequality. In the sections below, we present various forms of such constitutive models, for different classes of inelastic material behaviors. Importantly, since ${\mathbf{F}}^{\alpha s}$ is a function of state, it follows that the reference configurations ${\mathbf{X}}^{\alpha }$ are not observable. While ${\mathbf{X}}^{\alpha }$ could be obtained by integrating eq.(4) for an observed ${\mathbf{F}}^s$ and a postulated ${\mathbf{F}}^{\alpha s}$, it cannot be measured directly.

3.2. Objectivity

The mapping of eq.(4) between the postulated generation $\alpha$ and the observable master generation $s$ must satisfy objectivity. Let $\mathbf{Q}$ be an orthogonal transformation, then ${\mathbf{F}}^{s*}=\mathbf{Q}\cdot {\mathbf{F}}^s$ represents the transformation of ${\mathbf{F}}^s$ by $\mathbf{Q}$, since the deformation gradient is a two-point tensor. If we adopt the constitutive assumption that the mapping ${\mathbf{F}}^{\alpha s}$ constrains ${\mathbf{F}}^{\alpha }$ to be a deformation gradient, it follows that ${\mathbf{F}}^{\alpha *}=\mathbf{Q}\cdot {\mathbf{F}}^{\alpha }$ is the transformation of ${\mathbf{F}}^{\alpha }$ by $\mathbf{Q}$, for all $\alpha$. Substituting these two transformations into eq.(4), we find that ${\mathbf{F}}^{s*}={\mathbf{F}}^{\alpha *}\cdot {\mathbf{F}}^{\alpha s}$, which confirms that ${\mathbf{F}}^{\alpha s}$ is a material tensor that must be formulated as a mapping within the material frame (i.e., between ${\mathbf{X}}^s$ and ${\mathbf{X}}^{\alpha }$ such that ${\mathbf{F}}^{\alpha s*}={\mathbf{F}}^{\alpha s}=\partial {\mathbf{X}}^{\alpha }/\partial {\mathbf{X}}^s$).

We use the polar decomposition theorem to decompose ${\mathbf{F}}^{\alpha }$ into ${\mathbf{R}}^{\alpha }\cdot {\mathbf{U}}^{\alpha }$, where ${\mathbf{R}}^{\alpha }$ is the rotation tensor and ${\mathbf{U}}^{\alpha }$ is the right-stretch tensor of ${\mathbf{F}}^{\alpha }$. Thus, the mapping of eq.(4) takes the alternative form

$${\mathbf{U}}^s=\underset{{\mathbf{R}}^T}{\underbrace{{\left({\mathbf{R}}^s\right)}^T\cdot {\mathbf{R}}^{\alpha }}}\cdot {\mathbf{U}}^{\alpha }\cdot {\mathbf{F}}^{\alpha s}={\mathbf{R}}^T\cdot {\mathbf{U}}^{\alpha }\cdot {\mathbf{F}}^{\alpha s}$$ (5)

where $\mathbf{R}={\left({\mathbf{R}}^{\alpha }\right)}^T\cdot {\mathbf{R}}^s$ represents the relative rotation from line elements $d{\mathbf{X}}^s$ to $d{\mathbf{X}}^{\alpha }$ in the absence of stretching (i.e., when ${\mathbf{U}}^s={\mathbf{U}}^{\alpha }=\mathbf{I}$). We may rearrange this expression as

$$F^{\alpha s}={\left(U^{\alpha }\right)}^{-1}\cdot R\cdot U^s,$$ (6)

where it should be recalled that ${\mathbf{F}}^{\alpha s}$ is time-invariant, even though terms on the right-hand side of this expression may vary over time. Now we recognize that two-point rotation tensors and material right-stretch tensors respectively transform according to ${\mathbf{R}}^{\alpha *}=\mathbf{Q}\cdot {\mathbf{R}}^{\alpha }$ and ${\mathbf{U}}^{\alpha *}={\mathbf{U}}^{\alpha }$, from which it follows that ${\mathbf{R}}^{*}=\mathbf{R}$. Therefore, the objectivity requirement ${\mathbf{F}}^{\alpha s*}={\mathbf{F}}^{\alpha s}$ is consistently satisfied by eq.(6)

Finally, the formulation of a suitable constitutive model for ${\mathbf{F}}^{\alpha s}$, at time $t^{\alpha }$ when generation $\alpha$ is created, can be obtained by formulating suitable expressions for the right-stretch tensor ${\mathbf{U}}^{\alpha }$ and the relative rotation $\mathbf{R}$ at time $t^{\alpha }$ [10]. For example, the simplest constitutive model for $\mathbf{R}$, generally suitable for isotropic materials, is to set it equal to the identity tensor $\mathbf{I}$ for all $t\ge t^{\alpha }$.

3.3. Governing Equations

The referential apparent density ${\rho }_r^{\alpha }$ of constituent $\alpha$ is the ratio of the elemental mass $d{m}^{\alpha }$ of $\alpha$ in the current configuration, normalized by the referential elemental volume $d{V}_r$ of the mixture in the oldest generation. Here, ${\rho }_r^{\alpha }$ exclusively represents a compositional measure of constituent $\alpha$ in the mixture, in the form of a mass concentration. As shown by Bowen [18], the axiom of mass balance for components $\alpha$ of a constrained reactive mixture takes the form

$${\dot{\rho }}_r^{\alpha }={\widehat{\rho }}_r^{\alpha },$$ (7)

where the dot operator in ${\dot{\rho }}_r^{\alpha }$ denotes the material time derivative, and ${\hat{\rho }}_r^{\alpha }$ is a function of state that denotes the referential mass density supply to constituent $\alpha$, due to reactive mass exchanges with all other mixture constituents. Constitutive models for ${\hat{\rho }}_r^{\alpha }$ will also be illustrated in the sections below. It should be evident from eq.(7) that ${\rho }_r^{\alpha }$ remains constant in the absence of reactions involving constituent $\alpha$ (when ${\hat{\rho }}_r^{\alpha }=0$), regardless of the state of deformation at the current time $t$.

In general mixtures [18], the axiom of mass balance for the mixture requires that

$$\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }=0,$$ (8)

implying from eq.(7) that the referential mass concentrations ${\rho }_r^{\alpha }$ of all constituents in a constrained mixture must satisfy

$$\sum _{\alpha }{\rho }_r^{\alpha }={\rho }_r,$$ (9)

where ${\rho }_r$ is the constrained mixture mass density.

In an isothermal framework where temperature is temporally constant and spatially uniform, the state variables for a constrained mixture may be reduced to $\left({\mathbf{F}}^s,{\rho }_r^{\alpha }\right)$. This set of state variables is limited to the observable deformation gradient of the master generation, and the measurable composition ${\rho }_r^{\alpha }$ of all mixture constituents $\alpha$. The corresponding referential (Helmholtz) free energy density of the mixture is

$${\Psi }_r=\sum _{\alpha }{\rho }_r^{\alpha }{\psi }^{\alpha }\left(F^s,{\rho }_r^{\beta }\right),$$ (10)

where ${\psi }^{\alpha }$ is the specific (Helmholtz) free energy of constituent $\alpha$, and ${\rho }_r^{\beta }$ spans all $\alpha$. As shown in [13], satisfying the Clausius-Duhem inequality for arbitrary processes produces the classical hyperelasticity constraint for the mixture stress,

$$\mathbf{\sigma }=J^{-1}\frac{\partial {\Psi }_r}{\partial F^s}\cdot {\left(F^s\right)}^T,$$ (11)

leaving the residual dissipation statement

$$\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }{\mu }^{\alpha }\le 0.$$ (12)

Here, the term ${\mu }^{\alpha }$ represents the chemical potential of constituent $\alpha$, defined by

$${\mu }^{\alpha }=\frac{\partial {\Psi }_r}{\partial {\rho }_r^{\alpha }}.$$ (13)

The inequality of eq.(12) is commonly encountered in the physical chemistry of reactive mixtures, where it is generally described as the requirement for a chemical reaction to proceed spontaneously (i.e., without the addition of heat). It should be noted that, in classical physical chemistry, a process taking place at constant volume is equivalent to keeping the solid deformation gradient ${\mathbf{F}}^s$ constant in our list of state variables. Consequently, substituting eqs.(7) and (13) into the residual dissipation statement of eq.(12), and integrating the resulting expression with respect to time while keeping ${\mathbf{F}}^s$ constant, produces the more traditional form of this constraint,

$${\Delta \Psi }_r\le 0\text{ at constant volume },$$ (14)

where $\Delta {\Psi }_r={\Psi }_r^{\text{final}}-{\Psi }_r^{\text{initial}}$. This expression requires that there should be a net decrease in the referential (Helmholtz) free energy density of the mixture between final and initial states, when reactions take place under isothermal and isochoric conditions.

However, in a continuum mechanics framework, we do not adopt the assumption that ${\mathbf{F}}^s$ is constant, thus we should use the rate form of eq.(12) to place constraints on the functions of state that remain unconstrained so far, namely, the mapping ${\mathbf{F}}^{\alpha s}$ between the reference configurations of constituent $\alpha$ and the master generation, as illustrated in the sections below.

Finally, it should be noted that the free energies (either ${\Psi }_r$ or ${\psi }^{\alpha }$) all represent measures of strain energy in an isothermal framework, since the temperature-dependent contribution to the free energy remains constant under isothermal conditions, and this constant may be arbitrarily set to zero [13].

The linear momentum balance for the mixture reduces to the traditional form

$$\text{div}\mathit{\sigma }+\rho \mathbf{b}=\rho \mathbf{a}$$ (15)

where $\rho ={\sum }_{\alpha } {\rho }_r^{\alpha }/J^s$ is the mixture density and $J^s=\text{det}{\mathbf{F}}^s,\mathbf{b}$ is the specific body force, and $\mathbf{a}$ is the mixture acceleration (the material time derivative of the common velocity ${\mathbf{v}}^s$ of all constituents). The mixture angular momentum balance may be satisfied by eq.(15), as long as we require $\mathit{\sigma }$ to be symmetric, ${\mathit{\sigma }}^T=\mathit{\sigma }$.

3.4. Ideal Simple Mixtures

As outlined in Section 3.3, the specific free energy ${\psi }^{\alpha }$ of mixture constituent $\alpha$ in an isothermal framework is generally a function of the state variables $\left({\mathbf{F}}^s,{\rho }_r^{\beta }\right)$, where $\beta$ spans all $\alpha$. For fluid solutions, this dependence of ${\psi }^{\alpha }$ on the concentrations ${\rho }_r^{\beta }$ of all constituents is essential for recovering classical relations for the chemical potential of ideal and non-ideal solvent and solutes reported in physical chemistry [40].

However, for constrained mixtures of solid constituents, we may adopt the modeling simplification that the specific free energy ${\psi }^{\alpha }$ of each constituent depends at most on its own concentration ${\rho }_r^{\alpha }$, as well as the deformation gradient ${\mathbf{F}}^s$, with the understanding that this dependence on ${\mathbf{F}}^s$ may be via ${\mathbf{F}}^{\alpha }$ and the associated constitutive model for ${\mathbf{F}}^{\alpha s}$, as per eq.(4). We refer to this type of mixture as an ideal simple mixture.¹

Substituting this simplification into eq.(10) and the resulting expression into eq.(13) shows the chemical potential of constituent $\alpha$ in an ideal simple mixture reduces to

$${\mu }^{\alpha }={\psi }^{\alpha }+{\rho }_r^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\rho }_r^{\alpha }}.\text{ ideal simple mixture}$$ (16)

Recall that ${\psi }^{\alpha }$ reduces to the specific strain energy of constituent $\alpha$ in the context of isothermal processes, consequently the dependence of ${\psi }^{\alpha }$ on ${\rho }_r^{\alpha }$ implies that material properties of the solid constituent $\alpha$ are functions of ${\rho }_r^{\alpha }$. Thus, a stress-free state, which normally implies a state of strain that produces ${\psi }^{\alpha }=0$, also implies that this state of strain will produce $\frac{\partial {\psi }^{\alpha }}{\partial {\rho }_r^{\alpha }}=0$, and thus ${\mu }^{\alpha }=0$, as illustrated in an example below. This simplification allows us to provide a more intuitive application of the residual dissipation statement of eq.(12) to the case of constrained reactive solid mixtures,

$$\sum _{\alpha }{\widehat{\rho }}_r^{\alpha }\left({\psi }^{\alpha }+{\rho }_r^{\alpha }\frac{\partial {\psi }^{\alpha }}{\partial {\rho }_r^{\alpha }}\right)\le 0,\text{ ideal simple mixture}.$$ (17)

In general, the specific strain energy ${\psi }^{\alpha }$ is a positive semi-definite function of strain measures derived from ${\mathbf{F}}^s$ (or ${\mathbf{F}}^{\alpha }$), and in the case of ideal simple mixtures it follows that ${\mu }^{\alpha }$ in eq.(16) behaves similarly as a function of strain. This observation makes it easier to enforce the residual dissipation statement in eq.(17), as outlined in the sections below.

As a final note in this section, because of the simplification adopted for this type of ideal mixture, the summation in eq.(17) is taken over solid constituents only, implying that the mixture only includes constrained solid constituents. Thus, any putative chemical energy produced from reactions involving (unconstrained) fluid constituents is being neglected in this ideal simple mixture model.

Example 1. Trabecular Bone Chemical Potential

For example, in the field of trabecular bone growth and remodeling, it may be assumed that trabecular bone behaves as a linear isotropic elastic solid, but its Young’s modulus depends nonlinearly on its apparent mass density. In the notation of this study, we may propose that the strain energy density for this material takes the form

$${\rho }_r^{\alpha }{\psi }^{\alpha }=E^{\alpha }{\mathit{\epsilon }}^{\alpha }:{\mathit{\epsilon }}^{\alpha },$$ (18)

where $E^{\alpha }$ is Young’s modulus, which may depend on ${\rho }_r^{\alpha }$, and ${\mathit{\epsilon }}^{\alpha }$ is the infinitesimal strain tensor derived from ${\mathbf{F}}^{\alpha }$ for generation $\alpha$. This simplified model assumes that Poisson’s ratio for this porous trabecular bone structure is zero, for illustrative purposes. A common finding in the trabecular bone literature is that $E^{\alpha }=c{\left({\rho }_r^{\alpha }\right)}^{\gamma }$, where the parameter $c$ and the exponent $\gamma$ are fitted material constants [36]. For this model, the chemical potential derived from eq.(16) takes the form

$${\mu }^{\alpha }=\gamma c{\left({\rho }_r^{\alpha }\right)}^{\gamma -1}{\mathit{\epsilon }}^{\alpha }:{\mathit{\epsilon }}^{\alpha }.$$ (19)

This example confirms our expectation that ${\mu }^{\alpha }$ is a positive semi-definite function of the strain ${\mathit{\epsilon }}^{\alpha }$, and thus a stress-free state for this material, which produces ${\psi }^{\alpha }=0$ when ${\mathit{\epsilon }}^{\alpha }=0$, also yields ${\mu }^{\alpha }=0$.

4. Multigenerational Interstitial Growth

Our multigenerational interstitial growth framework was first presented in [11]. In that original study, we proposed, by constitutive assumption, that a new generation $\alpha$ of solid matrix constituents being synthesized by cells at time $t^{\alpha }$, according to the reaction of eq.(1), was deposited in a stress-free state. In the context of the equations presented above, a stress-free state implies that ${\psi }^{\alpha }=0$ at time $t^{\alpha }$, whereas the synthesis of this $\alpha -$generation implies that ${\hat{\rho }}_r^{\alpha }>0$. Thus, this constitutive assumption satisfied the residual dissipation statement of eq.(17).

To satisfy this constitutive assumption, we must also assume that ${\psi }^{\alpha }$ is explicitly a function of ${\mathbf{F}}^{\alpha },{\psi }^{\alpha }={\psi }^{\alpha }\left({\mathbf{F}}^{\alpha }\right)$, such that the right-stretch tensor ${\left.{\mathbf{U}}^{\alpha }\right|}_{t^{\alpha }}=\mathbf{I}$ at the time $t^{\alpha }$ when solid constituent $\alpha$ comes into existence (from reactive processes involving fluid constituents, not necessarily modeled explicitly in the mixture). In our original study [11], we also assumed implicitly that ${\left.\mathbf{R}\right|}_{t^{\alpha }}=\mathbf{I}$, as we had not yet established the objectivity requirements that are now summarized in Section 3.2. Therefore, according to eq.(6), the constitutive model for ${\mathbf{F}}^{\alpha s}$ must take the form

$$F^{\alpha s}={U^s|}_{t^{\alpha }},$$ (20)

showing that an expression for ${\mathbf{F}}^{\alpha s}$ is easily deduced from the observable deformation gradient (and thus, the right-stretch tensor) of the master generation.

Here, we clarify that the assumption that ${\left.\mathbf{R}\right|}_{t^{\alpha }}=\mathbf{I}$ remains valid even if the constituent $\alpha$ being deposited is fibrillar or fibrous (as in the case of collagen matrix constituents synthesized by cells), thus imparting material anisotropy. Indeed, in a growth framework, constituent $\alpha$ is not extant for times prior to $t^{\alpha }$. Thus, the unit vector orientation ${\mathbf{n}}_r^{\alpha }$ of a fibrous or fibrillar matrix constituent synthesized at time $t^{\alpha }$ is also defined only for times $t\ge t^{\alpha }$. It follows that the concept of a relative rotation of ${\mathbf{n}}_r^{\alpha }$ between configurations ${\mathbf{X}}^s$ and ${\mathbf{X}}^{\alpha }$ is irrelevant in this context.

In a practical growth theory, constitutive models for ${\widehat{\rho }}_r^{\alpha }$ must also be provided for completeness. In practice, suitable models for ${\widehat{\rho }}_r^{\alpha }$ are either characterized from experimental observations, as in tissue engineering studies [59, 60], or postulated by assumption [6, 8, 11, 56], as illustrated in an example below.

In summary, in a growth framework that satisfies the constraints and simplifications outlined in Section 3.4, new generations must be deposited in a stress-free state. Objectivity is satisfied as long as the mapping ${\mathbf{F}}^{\alpha s}$ is a material tensor given by the right-stretch tensor of the observable deformation gradient, at the time of synthesis, as given in eq.(20).

Example 2. Mass Growth from Nutrients

Consider that some nutrient $n$ is present in a mixture, and that cells consume this nutrient to produce a solid constituent $\alpha$. The reaction corresponding to this solid mass deposition (growth) process is

$$\text{cells}+\text{nutrient}n\to \text{cells}+\text{solid}\alpha \text{.}$$ (21)

Using the law of mass action, which is a standard constitutive model for chemical reactions [47], we can apply Michaelis-Menten kinetics as shown, for example, in [59] to formulate the constitutive model

$${\widehat{\rho }}_r^{\alpha }=k^{\alpha }\frac{{\rho }_r^n}{K_m+{\rho }_r^n},$$ (22)

where $k^{\alpha }$ is the maximum synthesis rate of $\alpha$, and $K_m$ is the Michaelis constant, which regulates how much of the nutrient consumption goes to maintain cell viability $\left({\rho }_r^n\ll K_m\right)$ and how much contributes to the synthesis of constituent $\alpha$. Based on the axiom of mass balance in eq.(7), this relation also produces ${\dot{\rho }}_r^{\alpha }$. Evidently, growth occurs for as long as nutrient $n$ is available in the mixture $\left({\rho }_r^n\ne 0\right)$. Integrating this ordinary differential equation produces a solution for ${\rho }_r^{\alpha }$, which may lead to changes in the mixture’s material properties, as illustrated in Example 1. When modeling this type of growth, the nutrient may be simplistically assumed available at a constant concentration ${\rho }_r^n$, leading to a constant growth rate $k{\rho }_r^n/K_m+{\rho }_r^n$. Alternatively, it may be assumed that the nutrient diffuses from an external bath, thus obeying the mass balance equation

$${\dot{\rho }}_r^n+J^s\text{div}{m}^n={\widehat{\rho }}_r^n,$$ (23)

where $J^s=\text{det}{\mathbf{F}}^s$ and ${\mathbf{m}}^n$ is the mass flux of solute $n$ relative to the solid constituent [7]. A constitutive model is needed to relate ${\mathbf{m}}^n$ to the gradient of the concentration ${\rho }_r^n$, as well as the convective flux of the solvent, requiring the specification of a diffusivity coefficient. Here, we would set ${\widehat{\rho }}_r^n=-{\widehat{\rho }}_r^{\alpha }$ based on the stoichiometry of the reaction in eq.(21). In this type of process, nutrients would get preferentially consumed by cells located closer to the scaffold boundary against the bath solution, leading to inhomogeneous growth of solid matrix constituents, as illustrated in prior studies [56, 59].

Example 3. Solid Mass Growth Without Shape Change

In many tissue engineering studies, cells are seeded in a highly porous scaffold, and the growth culture leads to filling of the pore space with solid matrix constituents synthesized by the cells, in the absence of external loading, with no concomitant change in scaffold shape (Figure 2). Consequently, in this type of growth, it is not necessary to introduce new generations $\alpha$ to account for changes of reference configurations, thus the only generation needed in that formulation is the master generation $s$, and the only deformation gradient is the observable ${\mathbf{F}}^s$.

Similarly, in the classical field of growth and remodeling of trabecular (spongy) bone, it has been noted that bone does not exhibit residual stresses, even though it actively remodels in response to changes in loading (also known as Wolff’s law). Since bone is typically subjected to cyclical stresses that span the range from compression to tension, it is assumed that different generations of bone deposition all share the same reference configuration ${\mathbf{X}}^s$. Let ${\rho }_r^s$ denote the referential mass density of trabecular bone. A popular constitutive model for bone growth and remodeling [35, 78] can be expressed as a constitutive model for ${\hat{\rho }}_r^s$, of the form

$${\widehat{\rho }}_r^s=B\left(\frac{{\Psi }_r}{{\rho }_r^s}-{\psi }_0\right)$$ (24)

where ${\psi }_0$ is a set point for the specific strain energy, above which the bone grows and below which it resorbs (hence, growth and remodeling), and $B$ is the remodeling rate. The constitutive model for the trabecular bone strain energy density ${\Psi }_r={\rho }_r^s{\psi }^s\left({\mathbf{F}}^s,{\rho }_r^s\right)$ may be given by the formulation of Example 1. Here, we use the FEBio software (febio.org) to simulate a rectangular beam, $10\text{cm}\times 2\text{cm}\times \frac{1}{2}\text{cm}$, fixed at both ends, and subjected to a uniform pressure of ${10}^6\text{dyn}/{\text{cm}}^2$ on its top surface. Assuming that the true mass density of bone is ${\rho }_T^s=2\text{g}/{\text{cm}}^3$, and that the initial value of ${\rho }_r^s$ is uniformly $1\text{g}/{\text{cm}}^3$, we can evaluate the temporal evolution of ${\rho }_r^s$ by letting $B={10}^{-3}$ in consistent CGS units (with time units being arbitrary), and ${\psi }_0=65.4\text{erg}/\text{g}$ (which is the average value of ${\psi }^s$ over the entire beam in its initial loaded configuration). We let $E=E_0{\left({\rho }_r^s/{\rho }_T^s\right)}^2$, with $E_0=1.2\times {10}^{11}\text{dyn}/{\text{cm}}^2$. The evolution of ${\rho }_r^s$ over time is displayed in Figure 4.

Figure 4:

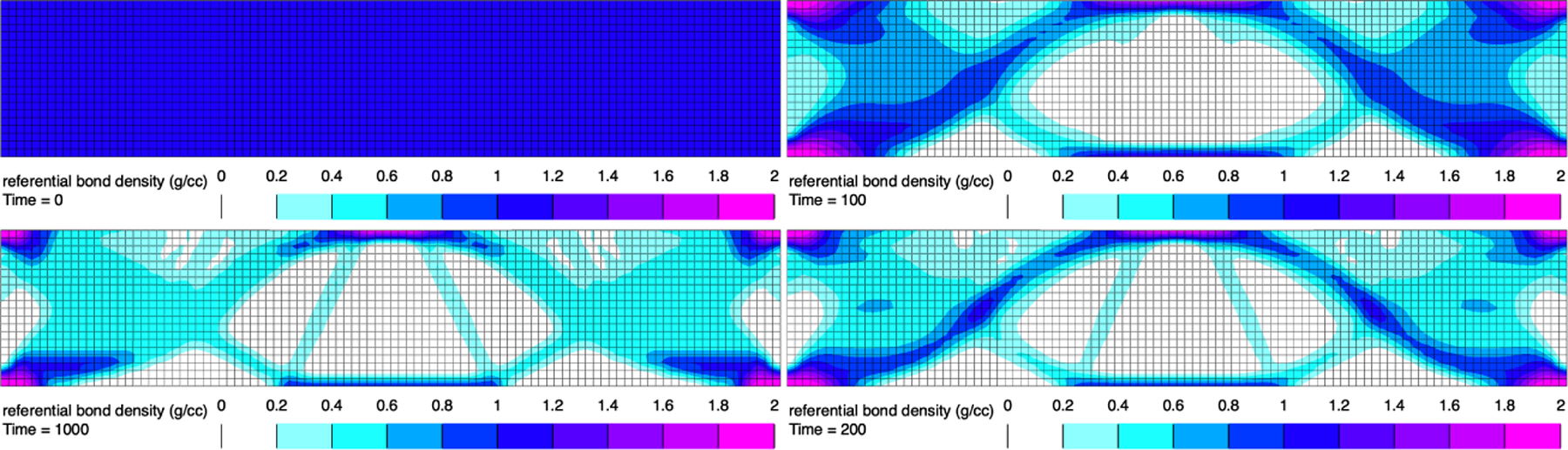
Finite element simulation of trabecular bone remodeling for a $10\text{cm}\times 2\text{cm}\times \frac{1}{2}\text{cm}$ beam, fixed at both lateral ends, and subjected to a uniform pressure of ${10}^6\text{dyn}/{\text{cm}}^2$ on its top surface (plane strain analysis). The referential apparent density ${\rho }_r^s$ is displayed at times 0 to 1000, clockwise from top left (arbitrary time units). Steady state was achieved at time 500 approximately. See Example 3 for additional details.

Example 4. Solid Mass Growth With Shape Change

In biological tissue growth, shape changes are often induced by osmotic swelling, which causes the interstitial fluid of porous cellular and tissue structures to pressurize, leading to the swelling of the porous solid matrix as fluid is drawn into the pore space. For example, cell proliferation typically occurs when a parent cell divides into two daughter cells of the same size as the parent, thus doubling the volume of cells (in an unconstrained environment). This mechanism involves doubling the ‘solid’ mass of cells (nuclear materials, such as DNA, and cytoskeletal structures, such as actin, myosin and microtubules) by drawing soluble nutrients and building materials from the interstitial fluid, as well as drawing extracellular water into the cells via osmotic gradients. In a mixture framework we may incorporate this osmotic swelling mechanism by letting the mixture stress include the osmotic fluid pressure $p$, such as $\mathit{\sigma }=-p\mathbf{I}+{\mathit{\sigma }}^s$, where ${\mathit{\sigma }}^s$ is the stress resulting from constrained solid mixture constituents such as the cytoskeleton. A constitutive model may then relate the pressure $p$ to the concentration of the intracellular ‘solid’ mass content in relation to extracellular osmolarity, and recalling that the intracellular concentration becomes diluted when water is drawn into the cell. Thus, the pressure $p$ may only rise transiently during cell proliferation, until the final intracellular concentration of ‘solid’ mass content of daughter cells matches that of the parent cell, or equivalently, when the intracellular osmolarity matches that of the extracellular environment [6, 8]. This transient rise in $p$ only needs to overcome the stress ${\mathit{\sigma }}^s$ of intracellular cytoskeletal structures to produce significant cell volume increase. Since it is well known that cytoskeletal structures, such as fibrillar actin, actively remodel in a cell (i.e., they break down into soluble form and regrow into fibrillar form in new reference configurations), the cytoskeletal stress ${\sigma }^s$ may return to zero after a cell division event. Illustrations of solid mass growth with shape changes, and solid matrix remodeling, are provided in [6, 8, 11, 56], using the growth framework outlined here.

Example 5. Multigenerational Growth

In this example, using FEBio, we illustrate a material with a ground matrix (compressible neo-Hookean [17], with Young’s modulus of 1 MPa and Poisson ratio of 0.3), and four generations of fiber bundles (tensile modulus of 5 MPa) being deposited over time in a mixture, with the first generation $s$ already present at time $t^s\to -\infty$, and subsequent generations $\alpha$ deposited at times $t^{\alpha }$, with $t^{\left(1\right)}=0.25,t^{\left(2\right)}=0.50$ and $t^{\left(3\right)}=0.75$. The tissue is subjected to a tensile strain of 10% over the time range $0 \le t \le 1.0,$ so that fiber generations (1) through (3) come into existence (are synthesized) as the tissue is being loaded. Each fiber generation is oriented along the loading direction and is deposted in a stress-free but uncrimped state. Thus, each fiber bundle becomes immediately engaged in the monotonically increasing loading response. The Cauchy stress-versus-time and Cauchy stress-versus-Hencky strain responses for this illustrative example are shown in Figure 5. Though each fiber behaves linearly in this range of strains, the mixture exhibits a nonlinear response, due to the multigenerational growth process. The prescribed strain on this tissue is decreased back to zero over the time range $1.0<t\le 2.0$. The complete temporal response in Figure 5a shows that the stress returns to zero in this material, implying that no residual stresses are produced during the growth process. The absence of residual stresses in this example can be attributed to the assumption that the fibers can only sustain tension but buckle in compression. Thus, as the tissue recoils during unloading, none of the fibers of the various generations can resist their compressive strains.

Figure 5:

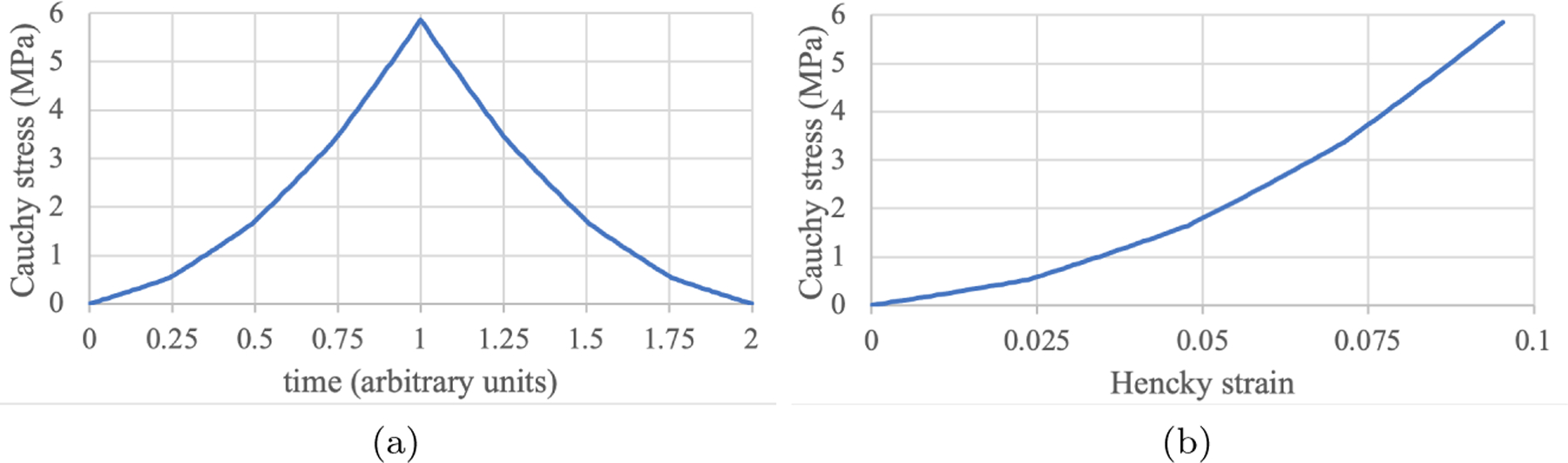
Multigenerational growth of fibers as described in Example 5. Cauchy stress versus (a) time, and (b) Hencky strain, showing normal stress and strain components along the loading direction, which coincides with the common orientation of all fibers. One fiber is present at the start of the analysis and the remaining three fibers are synthesized at times $t^{\left(1\right)}=0.25,t^{\left(2\right)}=0.50$ and $t^{\left(3\right)}=0.75$, respectively. Fibers behave linearly in this range of strains, but the mixture response is nonlinear due to the multigenerational growth process.

5. Reactive Damage Mechanics

As our cartilage tissue engineering culture conditions improved over time, we came to realize that negatively-charged proteoglycans, synthesized by chondrocytes at a hyper-physiologic rate, were producing excessive Donnan osmotic swelling. This type of osmotic swelling occurs when cations in the culture bath (such as Na⁺) transport into the tissue to neutralize the negatively-charged proteoglycans, causing an imbalance in osmolarity that drives water into the tissue, causing it to pressurize and swell. We hypothesized that this Donnan swelling-induced stretching of the fledgling, newly-synthesized collagen matrix, might produce levels of collagen stress that could cause it to get damaged. To test this hypothesis, we formulated a reactive damage theory consistent with reactive constrained mixture theory. This damage theory was then used to compare experimental tissue engineering results against model predictions of tissue swelling and damage, and verify if the model could properly predict experimental observations of excessive swelling, along with the observation that the equilbrium compressive modulus reached a plateau over time, even though matrix synthesis (proteoglycans and collagen) continued unabated [61].

We strived to formulate a theory that remained consistent with classical formulations of isotropic damage mechanics [20, 45], which generally rely on the framework of internal variable theory [26]. However, we aimed to formulate a damage framework, based on observable state variables, that would remain valid for anisotropic materials. Indeed, in our tissue engineering study, we compared our theoretical predictions of damage against an observable measure, obtained using a biochemical assay that could characterize the fraction of damaged collagen [14].

Here, we summarize the reactive damage mechanics framework resulting from that study. At a molecular level, consider that damage represents the permanent breaking of covalent bonds within collagen molecules. Therefore, the reaction being modeled in this theory is as follows:

$$\text{ intact covalent bonds }\stackrel{}{\stackrel{\text{loading}}{\to }}\text{ broken covalent bonds }$$ (25)

where the reaction is triggered by some measure related to tissue loading. If we denote intact bonds by $\alpha =s$, and broken bonds by $\alpha =b$, this reactive process only involves two solid mixture constituents in its simplest embodiment. Consistent with classical damage frameworks, we propose that a scalar failure criterion measure ${\Xi }^s\left({\mathbf{F}}^s\right)$ determines the threshold of loading at which intact bonds break. For example, ${\Xi }^s$ may represent the von Mises stress or the maximum principal stress in intact bonds. More specifically, damage progresses when ${\Xi }^s$ at the current time $t$ exceeds the maximum value ${\Xi }_m^s$ achieved over the prior history of loading,

$${\Xi }_m^s=\underset{-\infty <s\le t}{\text{max}}{\Xi }^s\left({F|}_s\right).$$ (26)

The referential mass concentrations of molecules associated with intact and broken bonds are, respectively, ${\rho }_r^s$ and ${\rho }_r^b$. According to eq.(9), they satisfy

$${\rho }_r={\rho }_r^s+{\rho }_r^b,$$ (27)

where ${\rho }_r$ is constant, but ${\rho }_r^{\alpha }$’s evolve in response to loading. For notational simplicity, we may refer to these as ‘bond concentrations’, though it should be understood that ${\rho }_r^{\alpha }$ refers to the mass of constituents that are associated with such bonds. More specifically, ${\rho }_r^{\alpha }$’s represent number densities of bonds $\alpha$, multiplied by ${\rho }_r$. We may thus define the mass fraction $w^{\alpha }$ of each bond family as

$$w^{\alpha }=\frac{{\rho }_r^{\alpha }}{{\rho }_r}.$$ (28)

Based on eq.(9), it follows that mass fractions sum to unity, ${\sum }_{\alpha } w^{\alpha }=1$.

A primary assumption of this reactive damage process is that intact bonds typically break progressively with increasing ${\Xi }_m^s$. The probability that intact bonds will break at a particular value of ${\Xi }_m^s$ is given by the probability density function $f^s\left({\Xi }_m^s\right)$, which is postulated by constitutive assumption. Then, the mass fraction of broken bonds at any given time is equal to the cumulative distribution function $F^s\left({\Xi }_m^s\right)$ associated with the p.d.f. $f^s\left({\Xi }_m^s\right)$,

$$w^b=F^s\left({\Xi }_m^s\right).$$ (29)

In analogy to classical theories of isotropic damage, we can define this mass fraction $w^b$ of broken bonds to be the damage variable $D$.

We assume that broken bonds cannot sustain any stress, thus ${\psi }^b=0$ is the constitutive model for these bonds. Consequently, it is not necessary to formulate a constitutive model for ${\mathbf{F}}^{sb}$ in this damage framework, since we never need to evaluate a putative ${\mathbf{F}}^b$. Based on eq.(10), we find that the strain energy density of this mixture is ${\Psi }_r={\rho }_r^s{\psi }^s$. In this damage framework we assume that the specific strain energy of intact bonds is independent of the concentrations ${\rho }_r^{\alpha }$, thus ${\psi }^s\equiv \psi \left({\mathbf{F}}^s\right)$. Now, we can rearrange the expression for ${\Psi }_r$ as

$${\Psi }_r=w^s{\Psi }_r^s=\left(1-w^b\right){\Psi }_r^s=\left(1-D\right){\Psi }_r^s,$$ (30)

where ${\Psi }_r^s={\rho }_r\psi \left({\mathbf{F}}^s\right)$ is the strain energy density of the material when all its bonds are intact. The associated mixture stress $\mathit{\sigma }$ is given by eq.(11),

$$\mathit{\sigma }=\left(1-D\right)J^{-1}\frac{\partial {\Psi }_r^s}{\partial F^s}\cdot {\left(F^s\right)}^T,$$ (31)

where $D=w^b$ is given in eq.(29). It is noteworthy that the expressions for ${\Psi }_r$ in eq.(30) and $\mathit{\sigma }$ in eq.(31) are consistent with classical relations of isotropic damage mechanics [20, 45].

To model damage in anisotropic materials, we may propose that the intact solid $s$ consists of a multitude of solid constituents $\sigma$, all sharing the same master reference configuration ${\mathbf{X}}^s$, such that ${\Psi }_r={\sum }_{\sigma } {\rho }_r^{\sigma }{\psi }^{\sigma }\left({\mathbf{F}}^s\right)$. Each constituent $\sigma$ may undergo damage based on its own distinct failure criterion ${\Xi }^{\sigma }\left({\mathbf{F}}^s\right)$, with its distinct c.d.f. $F^{\sigma }\left({\Xi }^{\sigma }\right)$, such that its mass fraction $w^{\sigma }$ evolves with damage according to $w^{\sigma }=w_0^{\sigma }\left(1-F^{\sigma }\left({\Xi }^{\sigma }\right)\right)$, where $w_0^{\sigma }$ is the initial mass fraction of $\sigma$ in the mixture, prior to damage. Then, ${\Psi }_r={\sum }_{\sigma } w^{\sigma }{\Psi }_r^{\sigma }$, where ${\Psi }_r^{\sigma }={\rho }_r^{\sigma }{\psi }^{\sigma }\left({\mathbf{F}}^s\right)$, and the mixture damage is given by $D={\sum }_{\sigma } w_0^{\sigma }{F}^{\sigma }\left({\Xi }^{\sigma }\right)$. Unlike classical damage theories for anisotropic materials, the damage variables remain scalar in this formulation, representing the fraction of intact bonds that have broken.

Example 6. Multigenerational Growth with Damage

In this example we reprise the illustrative multigenerational growth model of Example 5. Now, we allow each fiber bundle $\alpha$ in the multigeneration mixture to undergo damage in response to the magnitude $\Xi \left({\mathbf{F}}^{\alpha }\right)$ of the principal normal stress in that fiber generation, however we assume that the ground matrix does not get damaged in this simulation. We adopt a common Weibull distribution for the c.d.f. of all fiber bundles,

$$F\left({\Xi }^{\alpha }\right)=1-\text{exp}{\left(\frac{{\Xi }^{\alpha }}{\kappa }\right)}^{\gamma },$$

with $\kappa =2.5\text{MPa}$ and $\gamma =5$. The loading conditions remain the same as described in that earlier example. Here, the Cauchy stress-versus-Hencky strain response during loading and unloading is reported in Figure 6a. The stress-strain response of the damageable mixture evidently exhibits a hysteresis loop, as would be expected from the energy dissipated during the bond-breaking reactions. For comparison purposes, the intact response originally displayed in Figure 5b is superposed on the graph of Figure 6a, to better emphasize the change in tissue stress when damage is taking place. The corresponding damage $D$ which is the fraction of broken bonds in the mixture under the assumption that all four fiber bundles contribute an equal fraction of covalent bonds, is presented in Figure 6b. In this example, the damage $D$ accumulates monotonically during the loading phase $(0\le t\le 1.0)$, but remains constant during the unloading phase $(1.0<t\le 2.0)$, as would be expected.

Figure 6:

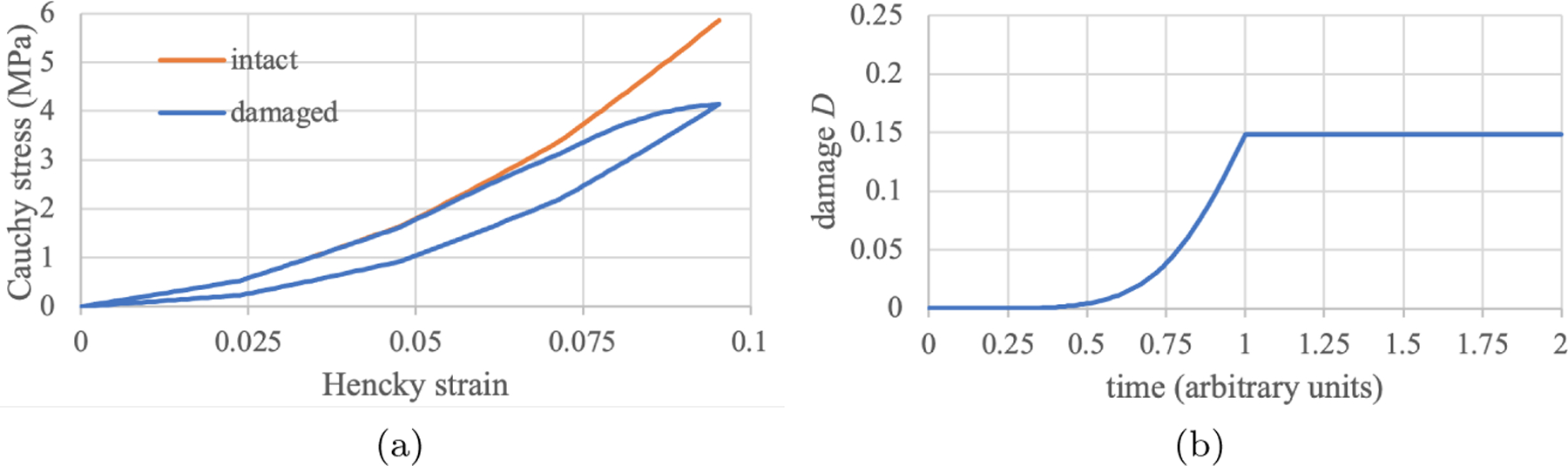
Multigenerational growth of fibers with damage, as described in Example 6. (a) Cauchy stress versus strain during loading and unloading, and (b) damage $D$ versus time. All fibers exhibit the same damage response, however individual fiber damage have different reference configurations due to multigenerational growth, implying that the maximum normal stress in each bundle is different. The hyesteresis loop in the stress-strain response reflects the energy dissipated due to damage.

6. Reactive Viscoelasticity

A viscoelastic material dissipates some of its stored strain energy into heat during loading. Green and Tobolsky [33] proposed that

…the internal processes of relaxation that are occurring in the material are characterized by equal rates of breaking and reforming of the bonds which constitute the network chain…

Based on this concept, we proposed a reactive theory of viscoelasticity where a material consists of strong bonds, which impart the elastic response to a viscoelastic material, and weak bonds, which break and reform according to Green and Tobolsky’s above description [5]. In an isothermal framework, it is implicitly assumed that the heat dissipated due to bond breaking-and-reforming in viscoelasticity is radiated away, while keeping the material at constant and uniform temperature.

At a molecular level, we may consider that covalent bonds represent the strong bonds in a viscoelastic material, whereas hydrogen bonds represent the weak bonds. Hydrogen bonds result from electrostatic attractive forces between electronegative and electropositive moieties of a single molecule, or multiple adjacent molecules, such as long polymeric chains that may fold, even when the net electric charge of those molecules is zero. It would be reasonable to assume that hydrogen bonds can break when loaded, without producing permanent damage to a polymeric network. They can reform in a stress-free state when electronegative and electropositive moieties come into sufficiently close proximity.

Damage to strong bonds can be described by the reactive damage framework outlined in Section 5. Therefore, the only reaction that needs to be taken into account in reactive viscoelasticity is the breaking-and-reforming of weak bonds. The general assumption of reactive viscoelasticity is that a reactive viscoelastic solid consists of a mixture of strong bonds $\alpha =e$ and weak bonds $\alpha =s$ at the resting start (master generation) of a loading analysis, both of which are in a stress-free state whose common reference configuration is ${\mathbf{X}}^s$. Upon loading, the loaded weak bonds in the $s$—generation begin to break and reform into a new, stress-free generation $u$. We denote the time of loading that initiates the $u$—generation as $t^u$. This breaking-and-reforming process is time-dependent, governed by reactive kinetics embodied in the constitutive model for ${\hat{\rho }}_r^{\alpha }$ as per eq. (7). Therefore, the concentration ${\rho }_r^s$ of weak bonds in generation $s$ decreases progressively with increasing time $t$, while the concentration ${\rho }_r^u$ of stress-free bonds increases accordingly, such that ${\rho }_r^s+{\rho }_r^u={\rho }_r$ remains constant and equal to the initial mass concentration of weak bonds. If the loading is changed again at time $t^v$, a new generation of stress-free bonds starts forming, called the $v$—generation, resulting from the breaking of extant $u$—generation bonds, such that ${\rho }_r^s+{\rho }_r^u+{\rho }_r^v={\rho }_r$. Thus, at times $t\ge t^u$, we have the single reaction

$$s—\text{generation stress-free hydrogen bonds}\stackrel{\text{loading}}{\to }u—\text{generation stress-free hydrogen bonds}$$ (32)

wherease at times $t\ge t^v$, we have another ongoing reaction,

$$u—\text{generation stress-free hydrogen bonds}\stackrel{\text{loading}}{\to }v—\text{generation stress-free hydrogen bonds}$$ (33)

For now, let us consider that the reactive mixture of weak bonds only consists of these three constituents, $\alpha =s,u,v$. We postulate that the constitutive models for ${\hat{\rho }}_r^{\alpha }$’s produce a solution for ${\rho }_r^s$ expressed in terms of its mass fraction $w^s$ as given in eq. (28), where

$$w^s=g\left({\left.{\mathbf{F}}^s\right|}_{t^u},t-t^u\right),t\ge t^u.$$ (34)

Here, $g$ is a reduced relaxation function whose functional form is a constitutive model. Thus, $g$ decreases monotonically from unity to zero as its time argument increases from zero to infinity. The explicit dependence of $g$ on the deformation gradient at the time of loading $t^u$ makes it possible to accommodate nonlinear viscoelasticity, via strain-dependent relaxation. According to eqs.(28) and (8), the corresponding solution for $w^u$ is $w^u=1-w^s$.

At time $t^v$, a second loading event takes place, which starts to break all the bonds that have reformed so far in a stress-free state. At this particular time, the mass fraction of stress-free reformed bonds is just ${\left.w^u\right|}_{t^v}$, therefore the solution for the now-breaking $w^u$ takes the form

$$w^u={f^u|}_{t^v}g\left({F^s|}_{t^v},t-t^v\right),t\ge t^v,$$ (35)

where ${\left.{\left.f^u\right|}_{t^v}\equiv w^u\right|}_{t^v}=1-{\left.w^s\right|}_{t^v}$ is the fraction of stress-free reformed bonds available to break at time $t^v$.

Now, for any number of consecutive generations, we can generalize this solution for $w^{\alpha }$ at time $t\ge t^{\beta }$, where $\beta$ is the generation that follows $\alpha$, as

$$w^{\alpha }={f^{\alpha }|}_{t^{\beta }}g\left({F^s|}_{t^{\beta }},t-t^{\beta }\right),t\ge t^{\beta },$$ (36)

where

$$f^{\alpha }=1-\sum _{\gamma <\alpha } w^{\gamma }t\ge t^{\alpha }$$ (37)

represents the fraction of stress-free reformed bonds available at any given time. This framework implies that the number of generations $\alpha$ in a reactive viscoelastic mixture may increase to infinity if there are infinite incremental changes in loading over time (as determined by changes in ${\mathbf{F}}^s$). These formulas also assume that $w^{\alpha }=0$ for $t<t^{\alpha }$

The strain energy density of the mixture may now be evaluated from eq.(10), under the constitutive assumption that all generations $\alpha$ of weak bonds belonging to the same ‘family’ share the same functional form of the specific strain energy, ${\psi }^{\alpha }\left(\mathbf{F}\right)\equiv \psi \left(\mathbf{F}\right)$ for all $\alpha$, which is independent of bond concentrations ${\rho }_r^{\beta }$,

$${\Psi }_r={\Psi }_r^e\left(F^s\right)+\sum _{\alpha }{w}^{\alpha }{\Psi }_0^a\left(F^{\alpha }\right).$$ (38)

Here, ${\Psi }_0^a={\rho }_r\psi$ is the strain energy density of weak bonds and ${\Psi }_r^e$ is that of the strong bonds. In this framework, since we assume that each generation $\alpha$ forms in a stress-free state starting at $t^{\alpha }$, the constitutive model for ${\mathbf{F}}^{\alpha s}$ may be derived from eq.(6) under the assumption that ${\left.{\mathbf{U}}^{\alpha }\right|}_{t^u}=\mathbf{I}$, thus

$$F^{\alpha s}={R\cdot U^s|}_{t^{\alpha }},$$ (39)

where $\mathbf{R}$ remains to be specified by constitutive assumption. The simplest constitutive model is to let $\mathbf{R}=\mathbf{I}$, implying that the reference configurations of line elements in ${\mathbf{X}}^{\alpha }$ need not rotate relative to ${\mathbf{X}}^s$. This assumption is generally valid for isotropic materials. However, when a material is fibrous, we may account for the fact that the referential unit vector ${\mathbf{n}}_r^s$ of each fiber bundle in the master generation may have rotated to ${\mathbf{n}}_r^{\alpha }$ in the reference configuration ${\mathbf{X}}^{\alpha }$ of the $\alpha$—generation. Thus, we may consider that ${\left.\mathbf{R}\right|}_{t^{\alpha }}$ is the relative rotation between ${\mathbf{n}}_r^s$ and ${\mathbf{n}}_r^{\alpha }$, for each fiber bundle in the mixture.

For completeness, we may also argue that a symmetry plane in any anisotropic material, with outward normal ${\mathbf{n}}_r^s$, may also shift its orientation to ${\mathbf{n}}_r^{\alpha }$ in generation $\alpha$. This shift may alter the degree of anisotropy of the reformed generation $\alpha$, relative to that of the master generation $s$, often reducing the material symmetry. For example, a material that starts out orthotropic, with three orthogonal planes of symmetry in generation $s$, may end up exhibiting triclinic anisotropy when the three planes no longer remain orthogonal to each other. By that argument, it would be necessary to formulate the constitutive model for the strain energy density $\psi$ of each generation such that it can accommodate the lowest possible symmetry that may be expected upon deformation. Indeed, this adjustment is properly accounted for when modeling a biological tissue as a mixture of an isotropic ground matrix and any number of fibers, as long as the formulation for $\psi$ of each fiber is properly set to depend on ${\mathbf{n}}_r^{\alpha }$

Given our assumption here, that $\psi$ for each generation $\alpha$ does not depend on concentrations, it follows from eq.(16) that the chemical potential ${\mu }^{\alpha }$ of each generation is equal to $\psi \left({\mathbf{F}}^{\alpha }\right)$. When generation $\alpha$ comes into existence at time $t^{\alpha }$, its ${\hat{\rho }}_r^{\alpha }$ is positive by definition, but since these $\alpha$—generation bonds are in a stress-free state it follows that ${\mu }^{\alpha }$ is zero and the residual dissipation statement in eq.(17) is satisfied at $t^{\alpha }$. For subsequent times $t>t^{\alpha }$, if follows from (36) that ${\hat{\rho }}_r^{\alpha }<0$ since the concentration of loaded $\alpha$—bonds decays monotonically over time. And since $\psi \left({\mathbf{F}}^{\alpha }\right)>0$ any time that these bonds are loaded, the residual dissipation statement is similarly satisfied for all times $t>t^{\alpha }$. In other words, the residual dissipation statement is satisfied if and only if generation $\alpha$ is produced in a stress-free state and the relaxation function $g$ decreases monotonically with time.

Implementation details for this reactive viscoelasticity framework have been presented recently [10], providing a reasonably efficient numerical scheme that caps the increasing number of generations with increasing time. A code implementation has been made available in the open-source finite element software FEBio (febio.org) [48, 49].

7. Reactive Plasticity

In a recent study [81], we reported our implementation of a reactive plasticity framework based on constrained reactive mixtures, which we proposed to model plasticity and elasto-plastic damage of amorphous materials. In this section we summarize the salient points of this formulation, in the context of the equations presented above.

To provide a molecular-level interpretation of plasticity and plastic damage, we may consider this inelastic material response in the context of metallic bonds, though other interpretations, such as Coulomb frictional sliding between intertwined microscopic fibrillar strands [69], may be adopted as well.

Below a certain threshold of loading, metallic bonds behave as ordinary covalent bonds (elasticity). In our conceptual approach, we consider that loaded metallic bonds can break and reform in a stressed state: This process occurs when a dislocation propagates through a material, allowing some atoms to change positions while still maintaining metallic bonds with neighboring atoms due to sharing of their outer electron shell (plasticity). Metallic bonds are in a stressed state because the dislocations occur only at some locations.

Damage occurs when a dislocation inserts sufficient distance between some of these atoms to prevent the sharing of electrons. In that case, we consider that the dislocated metallic bond has broken (plastic damage). We also consider that some atoms never dislocate during loading, thus maintaining their original reference configuration and producing a standard elastic response. Finally, we acknowledge that some of these bonds may break without prior dislocation of their associated atoms (elastic damage).

To model plasticity in a reactive framework, we first consider the simplest case when all intact metallic bonds present in a material (the master generation $\alpha =s$) yield at the same threshold ${\Phi }_m$ of the scalar yield measure $\Phi \left({\mathbf{U}}^s\right.$) (such as the von Mises stress). As noted previously [81], this assumption produces an elastic-perfect plasticity response. The reaction modeled in this process is

$$\text{ intact metallic bonds }s\stackrel{}{\stackrel{\text{loading}}{\to }}\text{ yielded metallic bonds }u,$$ (40)

with the yielding taking place at time $t^u$, when the $u$—generation comes into existence in a stressed state, implying that ${\left.{\mathbf{U}}^u\right|}_{t^u}\ne \mathbf{I}$. Instead, based on eq.(6), we need to provide a constitutive model for ${\mathbf{F}}^{\alpha s}$ of each generation $\alpha$, to allow the evaluation of

$${U^{\alpha }|}_{t^{\alpha }}={U^s|}_{t^{\alpha }}\cdot {\left(F^{\alpha s}\right)}^{-1},$$ (41)

under the constitutive assumption that $\mathbf{R}=\mathbf{I}$ for isotropic amorphous plasticity. In a simplified quasi-static framework we assume that this yielding reaction is instantaneous, thus $w^s=1-H\left(t-t^u\right)$ and $w^u=H\left(t-t^u\right)$, where $H(\cdot )$ is the Heaviside unit step function.²

A yield surface may be defined for the master generation, in the conventional manner of plasticity theory [41], as the surface $\phi \left({\mathbf{U}}^s\right)=\Phi \left({\mathbf{U}}^s\right)-{\Phi }_m$ whose tensorial normal is ${\mathbf{N}}^s=\partial \phi /\partial {\mathbf{U}}^s$. Similarly, the yield surface for the $u$—generation is $\phi \left({\mathbf{U}}^u\right)=\Phi \left({\mathbf{U}}^u\right)-{\Phi }_m$, with surface normal ${\mathbf{N}}^u=\partial \phi /\partial {\mathbf{U}}^u$. If loading of $u$—generation bonds pushes against this yield surface, a new generation $v$ will be produced at time $t^v$, by further yielding of generation $u$:

$$\text{yielded metallic bonds }u\stackrel{}{\stackrel{\text{loading}}{\to }}\text{ yielded metallic bonds }v\text{. }$$ (42)

Here again, in this elastic-perfect plasticity model of reactive plasticity, we assume that all $u$—generation bonds yield simultaneously at time $t^v$ to produce $v$—generation bonds. Thus, at any given time, the mixture only contains one extant constituent, which we denote generically by $\alpha$. Its reactive mass supply is given by the constitutive model

$${\widehat{\rho }}_r^{\alpha }=\rho r(\delta (t-t^{\alpha })-\delta (t-t^{\beta })),$$ (43)

where $\delta (\cdot )$ is the Dirac delta function, and generation $\beta$ represent the next yielded generation in this reactive plasticity process. This expression shows that yielded generation $\alpha$ comes into existence at time $t^{\alpha }$, and is completely replaced with constituent $\beta$ at the next yielding time $t^{\beta }$, thus ${\rho }_r^{\alpha }={\rho }_r\left(H\left(t-t^{\alpha }\right)-H\left(t-t^{\beta }\right)\right)$ and $w^{\alpha }=H\left(t-t^{\alpha }\right)-H\left(t-t^{\beta }\right)$.

The plastic consistency condition, which says that the material must remain on the yield surface $\phi$ during consecutive yielding events from time $t^{\alpha }$ to time $t^{\beta }$, produces the constraint

$${N^{\alpha }|}_{t^{\alpha }}:\left({U^{\beta }|}_{t^{\beta }}-{U^{\alpha }|}_{t^{\alpha }}\right)=0,$$ (44)

As shown in our earlier study [81], classical plasticity could be recovered by selecting the following constitutive model for ${\mathbf{F}}^{\alpha s}$ in consecutive generations,

$${\left({\mathbf{F}}^{\beta s}\right)}^{-1}={\left({\mathbf{F}}^{\alpha s}\right)}^{-1}\cdot \left(\mathbf{I}-\lambda {\stackrel{\mathbf{ˆ}}{\mathbf{N}}}^{\beta }\right),$$ (45)

where

$${\stackrel{\mathbf{ˆ}}{\mathbf{N}}}^{\beta }\equiv \frac{{\mathbf{N}}^{\beta }}{\sqrt{{\mathbf{N}}^{\beta }:{\mathbf{N}}^{\beta }}}$$ (46)

is the tensorial unit normal to the yield surface for generation $\beta$, and $\lambda$ is a non-dimensional scalar whose value is obtained by satisfying the plastic consistency condition of eq.(44) using eqs.(41) and (45). The recursive relation of eq.(45) starts with ${\mathbf{F}}^{\alpha s}=\mathbf{I}$ (since $\alpha =s$), when $\beta =u$ is the first generation to yield. Accordingly, based on eq.(41), it follows that ${\left.{\mathbf{U}}^u\right|}_{t^u}={\left.{\mathbf{U}}^s\right|}_{t^u}$ for this first yielded generation of bonds. If desired, isochoric plastic flow can be enforced by satisfying det ${\mathbf{F}}^{\alpha s}=1$ for all yielded generations $\alpha$ [81].

The strain energy density in this reactive plasticity framework may be reduced from eq.(10) to

$${\Psi }_r={\Psi }_0\left(F^{\alpha }\right),$$ (47)

where $\alpha$ is the sole extant generation (either intact or yielded) at any given time, implying that $w^{\alpha }=1$, and ${\mathbf{F}}^{\alpha }$ is evaluated from eq.(4). Here, ${\Psi }_0={\rho }_r\psi$ where $\psi$ is the constitutive model for the specific strain energy density, assumed to have the same functional form for each generation $\alpha$, and assumed to be independent of bond concentrations.

As mentioned above, this basic formulation of reactive plasticity accommodates elastic-perfect plasticity responses. We can generalize this formulation in two simple ways: (1) We can include a fraction $w^e$ of elastic bonds that never yield, in which case the strain energy density takes the slightly more general form

$${\Psi }_r=w^e{\Psi }_0\left(F^s\right)+\left(1-w^e\right){\Psi }_0\left(F^{\alpha }\right),$$ (48)

which describes an elastic-linear plasticity response. (2) We can consider that a material consists of multiple metallic bond families $\gamma$, each of which has a different yielding threshold ${\Phi }_m^{\gamma }$. The superposition of these bond families produces the characteristic “strain-hardening” behavior, similar to prior approaches in the plasticity literature [58, 79].

Finally, if we substitute eqs.(43) and (47) into the residual dissipation statement of eq.(17) and consider the time interval $t^{\alpha }\le t\le t^{\beta }$ for consecutive yielding events, we find that

$${\rho }_r\delta \left(t-t^{\alpha }\right)\psi \left({\mathbf{F}}^{\alpha }\right)-{\rho }_r\delta \left(t-t^{\beta }\right)\left(\psi \left({\mathbf{F}}^{\alpha }\right)-\psi \left({\mathbf{F}}^{\beta }\right)\right)\le 0.$$

In particular, at time $t^{\beta }$, this statement requires that $\psi \left({\left.{\mathbf{F}}^{\alpha }\right|}_{t^{\beta }}\right)\ge \psi \left({\left.FD20{\mathbf{F}}^{\beta }\right|}_{t^{\beta }}\right)$. In other words, the specific strain energy of the yielded generation $\beta$ must be less than the specific strain energy that the preceding generation $\alpha$ would have sustained, had it not yielded.

Extensive verifications, and validations of this reactive plasticity framework against experimental data, were reported in our previously-published study [81]. For an easy-to-access illustrative example, we refer the reader to the case study published on the febio.org website [1], which compares FEBio reactive plasticity results against experimental measurements for the square-cup deep-drawing benchmark problem described in [28] (Figure 7).

Figure 7:

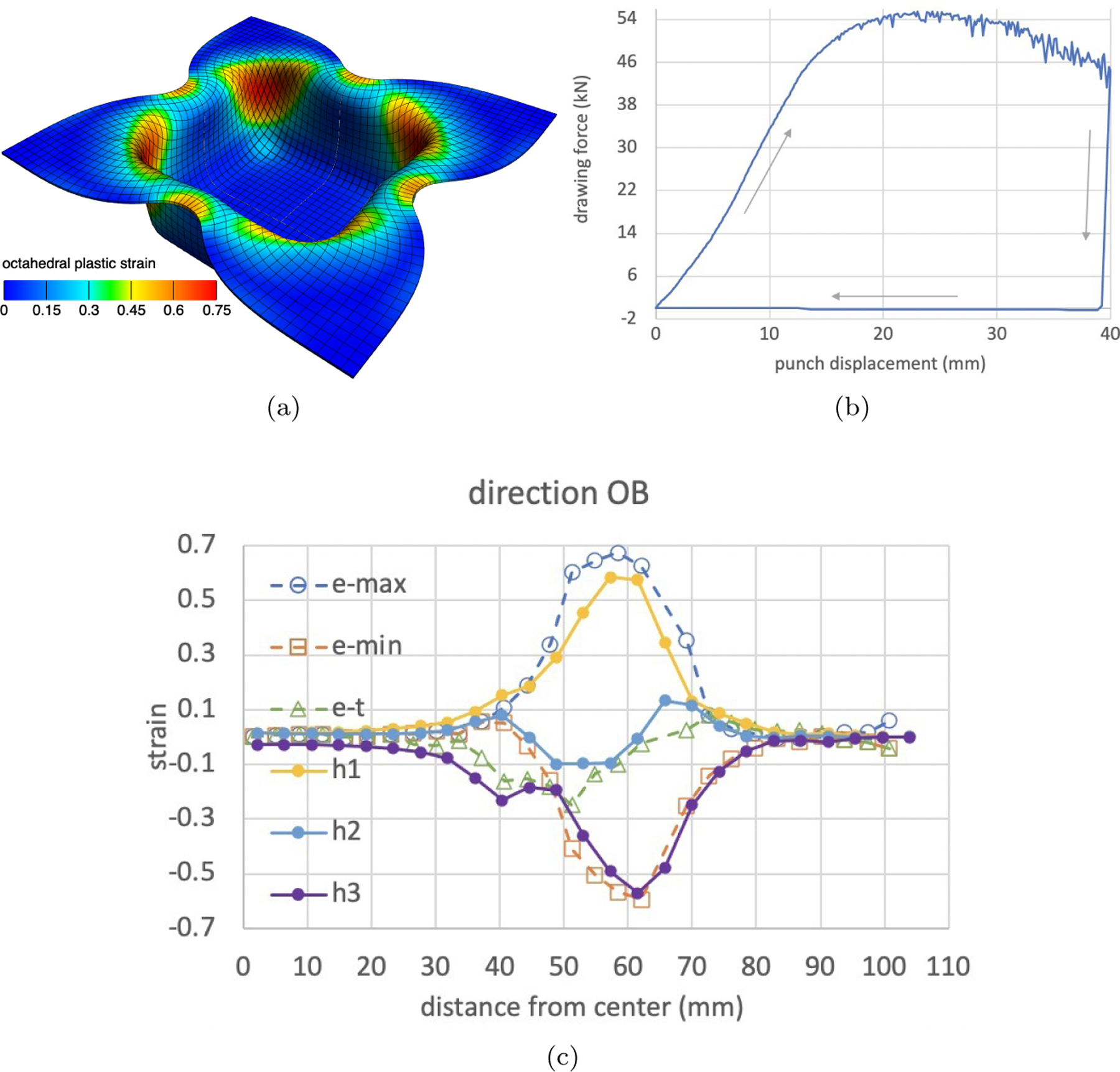
Square-cup deep-drawing benchmark problem in plasticity [28], solved using the reactive plasticity framework described in Section 7, using the FEBio open-source finite element software (febio.org). Details of the implementation can be found online [1]. (a) A flat square sheet, compressed between a rigid die and holder, turns into a cup when subjected to a deep-drawing deformation using a rigid square punch with rounded edges. This figure shows the final shape of the cup after the punch has been retrieved, and the color map shows the octahedral plastic strain. (b) Drawing force applied on punch to produce the cup. (c) Finite element (solid lines) and experimental (dashed lines) distribution of engineering strains along the diagonal line from the center of the plate to one of its corners, showing good agreement between model predictions (principal values $h_1,h_2$ and $h_3$ of the left Hencky strain tensor) and measurements (e-min, e-max for in-plane strains, and e-t for out-of-plane strain).

8. Discussion

This study reviews the modeling of various inelastic responses in solids, using the framework of constrained reactive mixtures. The presentation of governing equations in Section 3 provides the general formulation for these various inelastic responses. This formulation employs only observable state variables, namely the deformation gradient ${\mathbf{F}}^s$ and referential mass concentrations ${\rho }_r^{\alpha }$ in an isothermal context, in contrast to classical formulations of inelastic responses which rely on internal state variable theory [26]. In this framework, multiple solid generations $\alpha$ can co-exist at any given time in the mixture, constrained to share the same velocity ${\mathbf{v}}^s$ but distinct reference configurations ${\mathbf{X}}^{\alpha }$.

An important element of this formulation is that the time-invariant mapping ${\mathbf{F}}^{\alpha s}$ between these reference configurations ${\mathbf{X}}^{\alpha }$ and the observable master reference configuration ${\mathbf{X}}^s$ is a function of state, whose mathematical formulation is postulated by constitutive assumption as illustrated for growth in eq.(20), viscoelasticity in eq.(39), and plasticity in eq.(45). Accordingly, by definition, the configurations ${\mathbf{X}}^{\alpha }$ are not observable, consistent with the classical understanding of inelastic solid responses [65]. The function of state ${\mathbf{F}}^{\alpha s}$ is needed only to calculate the relative deformation gradient ${\mathbf{F}}^{\alpha }$ for generation $\alpha$; this treatment is consistent with the modern approach to inelasticity that recognizes measures of inelastic deformation are ill-defined and do not represent valid state variables [57, 68, 76] In the constrained reactive mixture approach, it is the observable composition ${\rho }_r^{\alpha }$ that evolves over time, as governed by the axiom of mass balance in eq.(7), which requires constitutive models for the mass density supplies ${\hat{\rho }}_r^{\alpha }$ as illustrated for growth models in eq.(22) and eq.(24), and plasticity in eq.(43), or the solution to the mass balance relation of eq.(7) as given for damage in eq.(29) and viscoelasticity in eq.(36), using mass fractions defined in eq.(28). We have provided a more detailed context of how our approach fits within more recent theories of plasticity in [81], particularly in relation to the work of [58, 79].

In essence, the classical approach and the constrained reactive mixture approach share considerable mathematical analogies, to the extent that they both introduce a multiplicative decomposition of the deformation gradient, and they both require evolution equations to track some of the state variables. However, they also differ at a fundamental level, since one adopts only observable state variables while the other introduces hidden state variables.

Another fundamental difference is that the mapping ${\mathbf{F}}^{\alpha s}$ in the constrained reactive mixture approach is time-invariant. Therefore, in a strict sense, ${\dot{\mathbf{F}}}^{\alpha s}=0$. Hence, it would be inappropriate to claim that the reference configuration of the mixture, or its constituents, “evolves” over time, since there is no single reference configuration in this type of mixture, nor is there a velocity associated with the evolution of each generation’s ${\mathbf{X}}^{\alpha }$. By extension, the temporal evolution of the response of a constrained reactive mixture can only be captured in the infinite summation of eq.(10). In contrast, in classical frameworks of quasilinear viscoelasticity [32, 34, 70], Boltzmann’s linear superposition principle has been employed to convert infinite summations to integrals over the time domain. However, the theoretical limitation imposed by this principle is the inability to model nonlinear responses, such as nonlinear viscoelasticity. Nevertheless, many authors have proposed successful nonlinear viscoelasticity formulations based on internal variable theory, which adopt assumptions that allow them to incorporate nonlinear evolution equations [3, 44, 66, 80], or strain-dependent relaxation functions [63].

The drawback from Boltzmann’s linear superposition principle does not exist in the constrained reactive mixture approach, since the summation of eq.(10) can easily accommodate nonlinear viscoelasticity, as indicated in Section (6). In practice, it is easy to convert the summation formulation into numerical implementations, as illustrated in the open-source finite element software FEBio. However, as acknowledged in our recent study [10], these numerical schemes are not as efficient as those employed using integrals based on the principle of linear superposition [64, 72], including those that use Prony series to approximate the solution to nonlinear evolution equations [80].

In summary, this review presents an alternative foundational approach to the modeling of inelastic responses in solids, grounded in the classical framework of mixture theory [15, 37, 74]. Applications to growth, damage mechanics, viscoelasticity and plasticity, demonstrate that this foundational approach is versatile and able to reproduce classical formulations, while also acommodating more complex behaviors, such as nonlinear viscoelasticity, that have been more difficult to formulate otherwise.

Highlights.

• This study reviews the progression of our research, from modeling growth theories for cartilage tissue engineering, to the formulation of constrained reactive mixture theories to model inelastic responses in any solid material, such as theories for damage mechanics, viscoelasticity, plasticity, and elasto-plastic damage.

• The framework used in this study is the theory of constrained reactive mixtures of solid constituents.

• Classical and constrained reactive mixture approaches share considerable mathematical analogies. However, they also differ at a fundamental level, since one adopts only observable state variables while the other introduces hidden state variables.