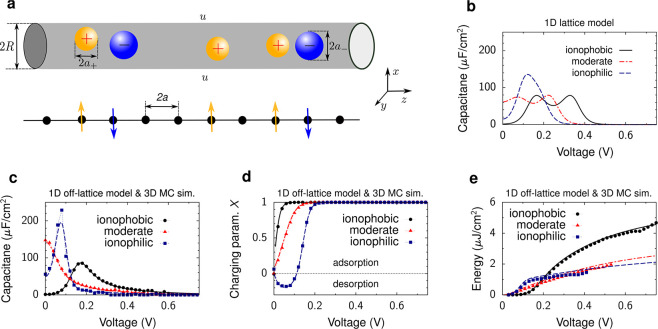
Figure 3.

Charge storage in single-file pores. (a) Model of a metallic cylindrical nanopore of radius R. An electrostatic potential difference u is applied to the nanopore with respect to bulk electrolyte (not shown). The ion radii are a = a_± < R. In 1D lattice and off-lattice models, the centers of ions and solvent molecules (if any) are located on the symmetry axis of the nanotube. In the lattice model, the ions are located on the lattice sites. The lower cartoon shows the lattice model with the arrows symbolizing the spins oriented up or down, corresponding to the cations and anions in the nanotube shown above. (b) Results of 1D spin–lattice mode given by eq 18 (lower cartoon in (a)). Capacitance is shown as a function of applied potential difference for strongly ionophilic (chemical potential μ_IL^(lat) = −0.961 eV) and ionophobic pores 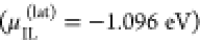, and for a pore moderately filled with ions . 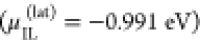(c–e) Results of 1D off-lattice model (lines) and 3D MC simulations (symbols). (c) Capacitance, (d) charging parameter X, 7, and (e) stored energy density are shown as functions of voltage. Parameter X > 0 (X < 0) corresponds to the charging driven by a combination of ion swapping and counterion adsorption (co-ion desorption). The chemical potentials were adjusted so as to provide the same in-pore ion densities as the lattice model in panel (b): μ_IL = −0.8 eV and μ_IL = −1.1 eV for the ionophilic and ionophobic pores, and μ_IL = −0.95 eV for the moderately filled pore. The plots have been created using the data from ref (44). In all plots, the ion radius a = 0.25 nm, the pore radius R = 0.26 nm, the in-pore dielectric constant ε = 2.5, and temperature T = 293 K.