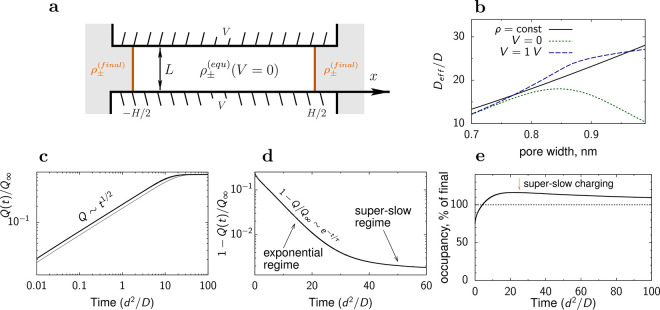
Figure 9.

Charging narrow slit nanopores. (a) Model of an open, slit-shaped metallic nanopore. Slit width L is comparable to the ion diameter, so that an ionic liquid is approximated as a 2D fluid (not shown). The in-pore ion densities at t = 0 are equilibrium densities at zero voltage. The ion densities at the pore entrances are the equilibrium densities at potential V applied to the slit walls with respect to bulk electrolyte (i.e., outside of the pore); these densities are kept constant at all times during charging. (b) Effective diffusion coefficient, eq 35, as a function of pore width for constant density and for two values of the applied potential V; the dependence of D_eff on V is through the ρ(V) dependence. (c,d) Accumulated charge as a function of time. The charge grows as a square-root of time at short times (c). At late times, there are two exponential regimes (d). (e) Pore occupancy with respect to the equilibrium occupancy at voltage V. Time is expressed in units of d²/D, where D is the diffusion coefficient and d the ion diameter. (b) Adapted with permission from ref (112). Copyright 2013 American Chemical Society. (a,c–e) Adapted with permission from ref (113). Copyright 2014 Springer Nature.