Julia for Biologists

Abstract

Biological research is becoming more computational. Collecting, curating, processing, and analysing large genomic and imaging datasets poses major computational challenges, as does simulating larger and more realistic models in systems biology. Here we discuss how a relative newcomer among computer programming languages – Julia – is poised to meet the current and emerging demands in the computational biosciences, and beyond. Speed, flexibility, a thriving package ecosystem, and readability are major factors that make high-performance computing and data analysis available to an unprecedented degree to “gifted amateurs”. We highlight how Julia’s design is already enabling new ways of analysing biological data and systems, and we provide a, necessarily incomplete, list of resources that can facilitate the transition into the Julian way of computing.

Computers are tools. Like pipettes or centrifuges, they allow us to perform tasks more quickly or efficiently; and like microscopes, they give us new, more detailed insights into biological systems and data. Computers allow us to develop, simulate and test mathematical models of biology and compare models to complex datasets. As computational power evolved, solving biological problems computationally became possible, then popular, and eventually, necessary [1]. Entire fields such as computational biology and bioinformatics emerged. Without computers, the reconstruction of structures from X-ray crystallography, NMR, or cryo-EM methods would be impossible. The same goes for the 1000 Genome Project [2], which used computer programs to assemble and analyze the DNA sequences generated. More recently, vaccine development has benefited from advances in algorithms and computer hardware [3].

Programming languages are also tools. They make it possible to instruct computers. Some languages are good at specific tasks – think Perl for string processing tasks; or R for statistical analyses – whereas others – including C/C++, and Python – have been used with success across many different domains. In biomedical research the prevailing languages have arguably been R [4] and Python [5]. Much of the high-performance backbone supporting computationally intensive research, hidden from most users, however, continues to rely on C/C++ or Fortran. Computationally intensive studies are often initially designed and prototyped in R, Python or Matlab, and subsequently translated into C/C++ or Fortran for increased performance. This is known as the two-language problem [6].

This two-language approach has been successful but has limitations. When moving an implementation from one language to another, faster, programming language, “verbatim” translation may not be the optimal route: faster languages often provide the programmer higher autonomy to choose how memory is accessed or allocated, or to employ more flexible data structures [7]. Exploiting such features may involve a complete rewrite of the algorithm [8, 9] to ensure faster implementations or better scaling as datasets grow in size and complexity. This requires expertise across both languages, but also rigorous testing of the code in both languages.

Julia [12] is a relatively new programming language that overcomes the two-language problem.Users do not have to choose between ease-of-use and high performance – Julia has been designed to be easy to program in and fast to execute [13]. This and the growing ecosystem of state-of-the-art application packages and introductions [9, 14] make it an attractive choice for biologists.

Biological systems and data are multifaceted by nature, and to describe them, or model them mathematically, requires a flexible programming language that can connect different types of highly structured data, see Figure 1. Three hallmarks of the language make Julia particularly suitable to meet current and emerging demands of biomedical science: speed, abstraction and metaprogramming.

Figure 1:

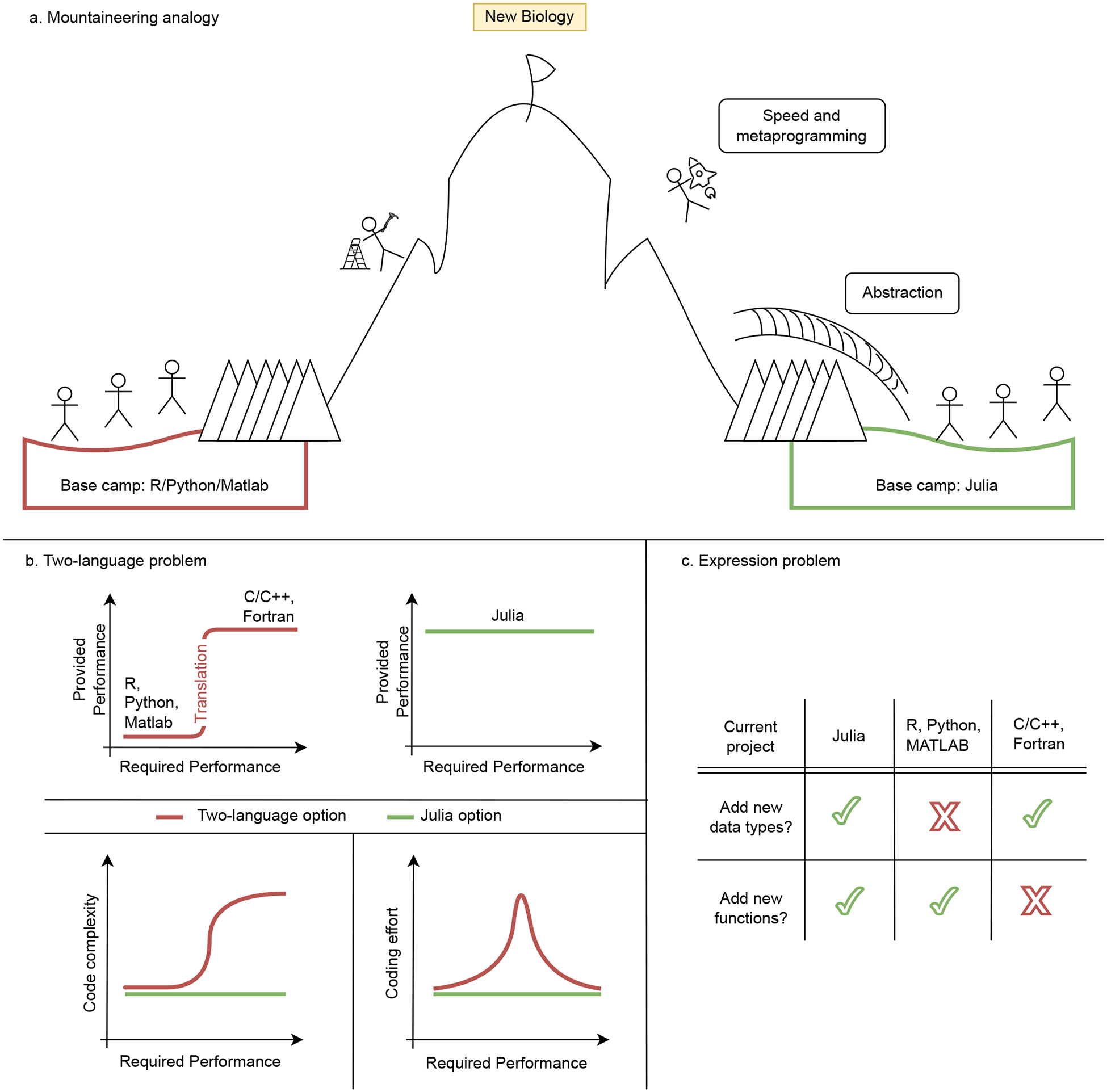
Julia is a tool for biologists to discover new science. (a) In the biological sciences, the most obvious alternative to the programming language Julia is R, Python or Matlab. Here, we contrast the two potential pathways to new biology with a mountaineering analogy: The top of the mountain represents “New Biology”[10, 11]. There are two potential base camps for the ascent: Base camp 1 (left, red) is “R/Python/Matlab”. Base camp 2 (right, green) is “Julia”. To get to the top, the mountaineer – representing a researcher – needs to overcome certain obstacles such as a glacier and a chasm. They represent research hurdles such as large and diverse datasets or complex models. Starting at the “Julia” base camp, the mountaineer has access to efficient and effective tools such as a bridge over the glacier and a rocket to simple fly over the chasm. They represent Julia’s top three language design features: Abstraction, speed and metaprogramming. With these tools, the journey to the top of the mountain becomes much easier for the excursionist. Julia allows biologists to not be hold back by problems discussed in (b) and (c). (b) The “Two-language problem” refers to having separate languages for algorithm development and prototyping (such as R or Python), and production-runs, such as (C/C++ or Fortran), respectively. Julia was designed to be good at both tasks, which can reduce programming efforts and software complexity. (c) The “Expression problem” refers to the effort required to define new (optimised) data types and functions that can be defined by users and added to existing external code bases.

Here we discuss each language feature and its biological relevance in the context of one concrete example per feature. An additional example per feature can be found in the Supplementary material. Further, we provide a summary of why we believe Julia is a good programming language for biologists in the Supplementary material (Table 2). Supporting online material is provided in the GitHub repository Perspective_Julia_for_Biologists^I. First, the online material shows code for the examples discussed here. Code examples have been chosen and designed to be accessible to a wide audience: we group them based on computational focus (high-level and low-level user case) and access points (e.g. Julia files and interactive notebooks). Second, a summary of helpful resources for starting with Julia and for building Julia solutions is provided. The latter include, for example: platform-specific Julia installation guides; links to introductory Julia courses; and a selection of pointers to relevant Julia communities.

Table 2:

As Julia is a relatively young language, it is safe to assume that the majority of biologists are not using Julia yet. In this table we present arguments that make Julia a good programming language for biologists.

1. Language design	Julia is user friendly. → It is easy to code. Julia is a high performance language. → It is fast. Julia offers a high level of abstraction. → It is flexible. Julia can be used for metaprogramming. → It can code automatically. Julia is not only good in one area but in many. → It enables “one language” projects.
2. Low barrier to entry	Easy to learn due to intuitive semantic and easy to read syntax. Accessible via various interfaces, REPL, IDE, or Jupyter notebook. Existing non-Julia code can be easily integrated into new Julia projects via language specific packages (Figure 4, Integration of non-Julia code).
3. Additional reasons	Julia is free, open-source and hosted on GitHub. Julia offers (generally) excellent documentation, tutorials, and help available directly from active and welcoming community members via various communication channels such as Slack, Discourse, Twitter or Zulip. Julia’s package ecosystem provides functionality for a wide range of oft-performed tasks in computational biology research (Figure 4, Table 1 in the main document). Julia code is smoothly extendable which enables and encourages easy contributions and collaborations to/with existing projects, as well as writing, integrating and sharing new, user specific packages.

Speed

The speed of a programming language is not just a matter of convenience that allows us to complete analyses more quickly. It can enable new and better science: speed is important for analysing large datasets [15, 16] that are becoming the norm across many areas of modern biomedical research [17]. Slow computations might not hold back scientific discovery when performed a small number of times. However, when performed repeatedly on large datasets, the execution speed of a programming language can become the limiting factor. Similarly, simulating large and complex computational models is only possible with fast implementations; digital twins [18, 19] in precision medicine, for example, will be useless without fast computation.

The speed of the programming language also determines how extensively we can test statistical analysis or simulation algorithms before using them on real data. Thorough testing of a new statistical algorithm can be expected to be around 2–3 orders of magnitude more costly in computational terms than a single “production run” [16]. Furthermore, the quality of approximations depends on many factors (e.g. number of tested candidates [20, 21] and grid step sizes [22]) and faster code enables better analysis. Here and in the Supplementary material we provide insights into the design features underlying Julia’s speed [6]. The speed rivals that of statically compiled languages such as Fortran and C/C++. Higher-level language features — hallmarks of R, Python, Matlab, and Julia — typically lead to shorter development times; going from an initial idea to working code can be orders of magnitude faster than for e.g. C/C++; this is in no small measure helped by the flexible Jupyter and Pluto.jl notebook user interfaces (which fulfil similar functions to e.g. R’s Shiny) and flexible software editing environments. Julia combines fast development with fast run-time performance and is therefore appropriate for both algorithm/method prototyping, and time and resource intensive applications.

Example: Network Inference from Single Cell Data.

In single cell biology, we can measure expression levels of tens of thousands of genes in tens of thousands of cells[24]. Increasingly we are able to do this with spatial resolution. But searching for patterns in complex and large data-sets is computationally expensive: even apparently simple tasks, such as calculating the mutual information (MI) across all pairs of genes in a large dataset can quickly become impossible.

Gene regulatory network (GRN) inference from single cell data is a statistically demanding task, and one where Julia’s speed helps. Chan et al. [16] use higher-order information theoretical measures to infer GRNs from transcriptomic single cell data of megakaryocyte-erythroid progenitor cells during human hematopoiesis [25], early embryonic development [26], and embryonic hematopoietic development [27]. The MI has to be calculated for gene pairs; but a multivariate information measure, partial information decomposition (PIDC), is also considered to separate out direct and indirect interactions [28], and this requires considering all gene triplets [29].

The run-time of algorithms implemented in the Julia package InformationMeasures.jl can be compared to the minet R package [30] (Figure 2(a) left). For small numbers of genes, differences are significant but not prohibitive: inferring a network with 100 genes takes around 0.3 seconds in Julia compared to 1.5 seconds in R; but already for 1,000 genes the inference times differ substantially: 17 seconds in Julia and 390 seconds (>20-fold difference) in R; for – by today’s standards small – datasets with 3,500 genes and 600 cells R needs over 2.5 hours, compared to Julia’s 134 seconds (64-fold difference); and in real-world applications [29] 400-fold speed differences are possible (this corresponds to computing times of hours versus weeks). Here we reach the threshold of what can be tested and evaluated rigorously in many highlevel languages. Overall, multivariate information measures would almost certainly be unfeasible in pure R or Python implementations.

Figure 2:

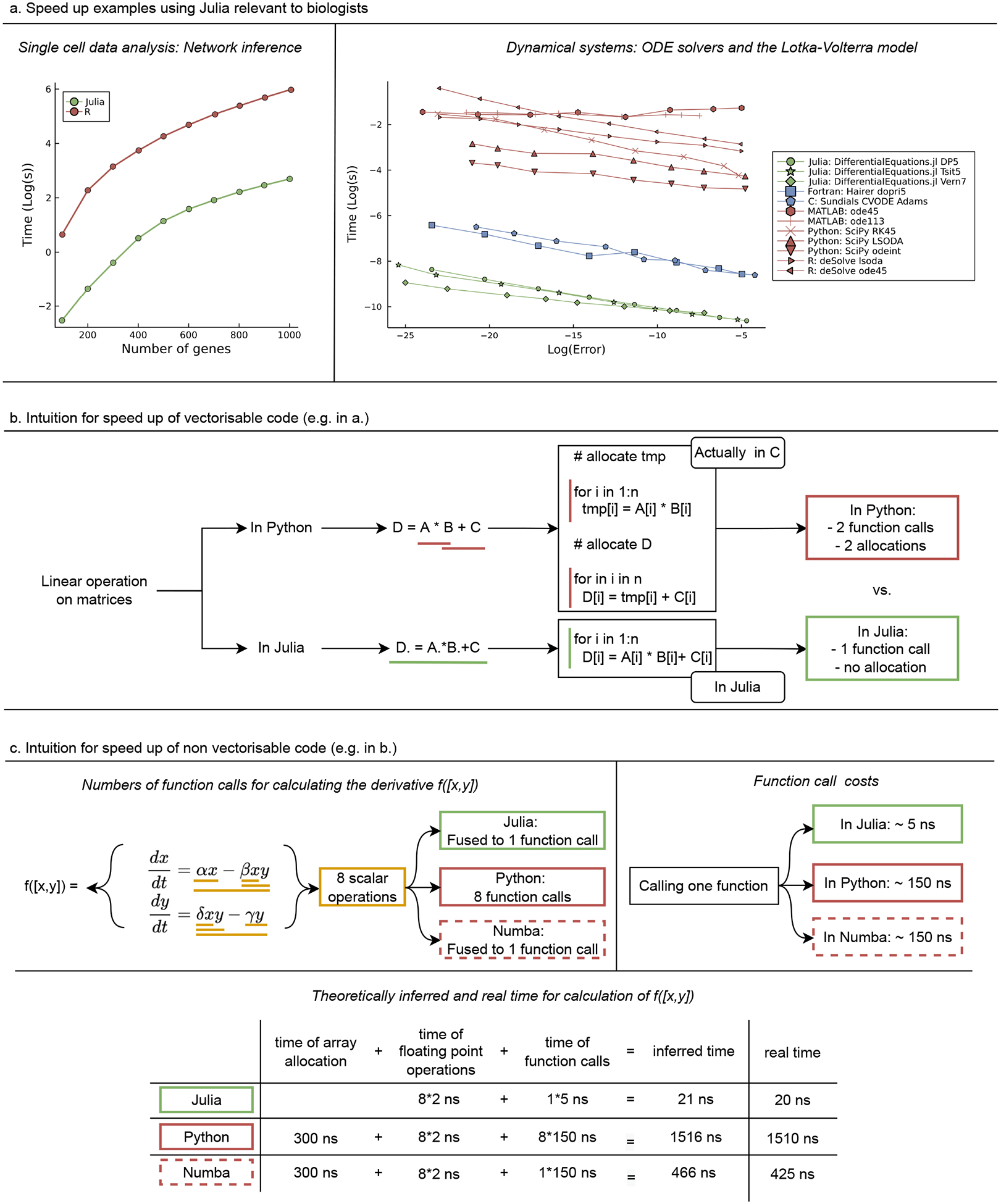
Julia’s speed feature. (a) Examples relevant to biology. Left: Comparison of time to calculate the mutual information for all possible pairs of genes of a single cell dataset [16]. Right: Benchmark of ODE solvers implemented in Julia and Fortran, C, MATLAB, Python, and R for the Lotka-Volterra model (More systems in [23]). (b) Illustration of speed-up of vectorisable code (as in (a)). (c) Intuition for speed up of non-vectorizable code (as in b).

The reason for this performance difference is Julia’s ability to optimize “vectorizable” code [6]; cf. Figure 2(b). Users of Python and R are familiar with vectorized functions, such as maps and element-wise operations. Julia’s performance improves by combining Just-in-Time (JIT) compilation – where computer code is compiled at run-time (and the compiler can therefore be informed by the current state of the program and data) rather than ahead of execution – with vectorized functions via a trick known as operator fusion. When writing a chain of vector expressions, like D=A*B+C (where A, B, C and D are n-dimensional vectors), libraries like NumPy call optimized code, which is typically written in languages like C/C++, and these operations are computed sequentially. For this example, A*B, C code is called to produce a temporary array, tmp, and then tmp+C is evaluated (using C) to produce D. Allocating memory for the temporary intermediate, tmp, and the final result D is O(n) (which means that the time it takes to complete the computation increases approximately linearly with n, the length of the vectors), and scales proportionally to the compute cost; thus no matter what the size of the vectors is, there is a major unavoidable overhead. Julia uses the “.” operator to signify element-wise action of a function, and we write D.=A.*B.+C. When the Julia compiler sees this so-called broadcast expression, it fuses all nearby dot operations into a single function, and JIT compiles this function a run-time into a loop. Thus NumPy makes two function calls and spends time generating two arrays, whereas Julia makes a single function call and reuses existing memory. This and similar performance features are now leading package authors of statistical and data science libraries to recommend calling Julia for such operations, such as the recommendation by the principal author of the R lme4 linear mixed effects library to use JuliaCall to access MixedModels.jl in Julia (both written by the same author) for an approximately 200x acceleration [31].

The code for this example can be found under the attached link^II.

Abstraction

Julia allows an exceptionally high level of abstraction [32]. We can illustrate the advantages of abstraction[33] by drawing an analogy to a standard lab tool: the pipettor. Pipettors produced by different manufacturers have slightly different designs; nevertheless they all perform the same task in a similar way. It thus takes minimum effort to get used to a new pipettor, without having to retrain on every aspect of an experimental protocol. Abstraction achieves the same for software [33]. Similar to the described abstract interface “pipettor”, in Julia we have interfaces such as the AbstractArray interface (discussed in detail in the SI). All its implementations are array-like structures that provide the same core functionalities which an array-like structure is expected to have. This allows us to easily and flexibly switch between different implementations of the same interface [34].

Abstraction is especially advantageous in the biological sciences where data is frequently heterogeneous and complex [35, 36, 37]. This can pose challenges for software developers [34] and data analysis pipelines as changes to data may require substantial rewriting of code for processing and analysis. We may either end up with separate implementations of algorithms for different types of data; or we may remove details and nuance from the data to enable analysis by existing algorithms. With abstraction we do not have to make such choices. Julia’s abstraction capabilities provide room for both specialisation and generalisation through features such as abstract interfaces and generic functions that can exploit the advantages of unique data formats with varying internal characteristics without an overall performance penalty. Here we illustrate the effect of Julia’s abstraction via an example of a structural bioinformatics pipeline. Additionally, we provide a second, more technical abstraction example focusing on image analysis in the Supplementary material.

Example: Structural bioinformatics with composable packages.

Julia’s flexibility means that packages from different authors can generally with ease be combined into workflows, a feature known as composability. Users benefit from Julia’s flexibility just as much as package developers. For example, we consider a standard structural bioinformatics workflow, where we want to download and read the structure of the protein crambin from the Protein Data Bank (PDB). This can be done using the BioStructures.jl package [38] from the BioJulia organisation, which provides the essential bioinformatics infrastructure. Protein structures can be viewed using Bio3DView.jl, which uses the 3Dmol.js JavaScript library [39] as Julia can easily connect to packages from other languages. We can show the distance map of the Cβ atoms using Plots.jl; while Plots.jl is not aware of this custom type, a Plots.jl recipe makes this straightforward. BioSequences.jl provides custom data types of sequences and allow us to represent the protein sequence efficiently. With this BioAlignments.jl can be used to align our sequences of interest. This suite of packages can be used to carry out single cell full-length total RNA sequencing analysis [40] quickly and with ease. A few lines of code in BioStructures.jl allow us to define the residue contact graph using Graphs.jl, giving access to optimised graph operations implemented in Graphs.jl for further analysis, such as calculating the betweenness centrality of the nodes. If coding and analysis are performed in Pluto.jl, then updating one section updates the whole workflow, which assists exploratory analysis.

Packages can be combined to meet the specific needs of each study; for example to generate protein ensembles and predict allosteric sites [41], or to carry out information theoretical comparisons using the MIToS.jl package [42]. In this example we have used at least five different packages together seamlessly. Plots.jl, BioAlignments.jl and Graphs.jl do not depend on, or know about BioStructures.jl but can still be used productively alongside it. Abstraction means that the improvements in any of these packages will benefit users of BioStructures.jl, despite the packages not being developed with protein structures in mind.

Package composability is common across the Julia ecosystem and is enabled by abstract interfaces supported by multiple dispatch, i.e. the ability to define multiple versions of the same function with different argument types (see e.g. [43] for examples of multiple dispatch). Programmers can define standard functions such as addition and multiplication for their own types; abstraction means that functions in unrelated packages often “just work” despite knowing nothing about the custom types. This is rarely seen in languages such as Python, R and C/C++, where the behaviour of an object is tightly confined [33] and combining classes and functions from different projects requires much more (of what is known as) “boilerplate” code.

For example, the Biopython project [44] has become a powerful package covering much of bioinformatics. But extensions to Biopython objects are generally added to (an increasingly monolithic) Biopython, rather than to independent packages. This can lead to objects and algorithms that have the difficult task of fitting all use cases, including their dependencies, simultaneously [45]. By contrast, Julia’s composability facilitates writing generic code that can be used beyond its intended application domain[43]. Tables.jl, for example, provides a common interface for tabular data, allowing generic code for common tasks on tables; currently, some 131 distinct packages draw on this common core for purposes far beyond the initially conceived application scope. This is an example that showcases how abstraction ensures interoperability and longevity of code.

The code for this example can be found under the attached link^III.

Metaprogramming

As our knowledge of the complexity of biological systems increases so does our need to construct and analyse mathematical models of these systems. Currently, most modeling studies in biology rely on programming languages that treat source code as static: once written, it can be processed into loaded and executing code, but it is never changed while running. We can compare this linear control process to the central dogma of biology [46, 47]: Source code (DNA) is transformed into loaded code (RNA), and executing code (protein). We now know that this process (DNA→RNA→Protein) is not linear and unidirectional: RNA and proteins can alter how and when DNA is translated. Programming languages that support metaprogramming break the linear flow of the computer program in a analogous manner. With metaprogramming, source code can be written that is processed into loaded and executing code and that can be modified during run-time. This shifts our perception from static software to code as a dynamic instance where the program can modify aspects of itself during run-time (Figure 6(a)).

Figure 6:

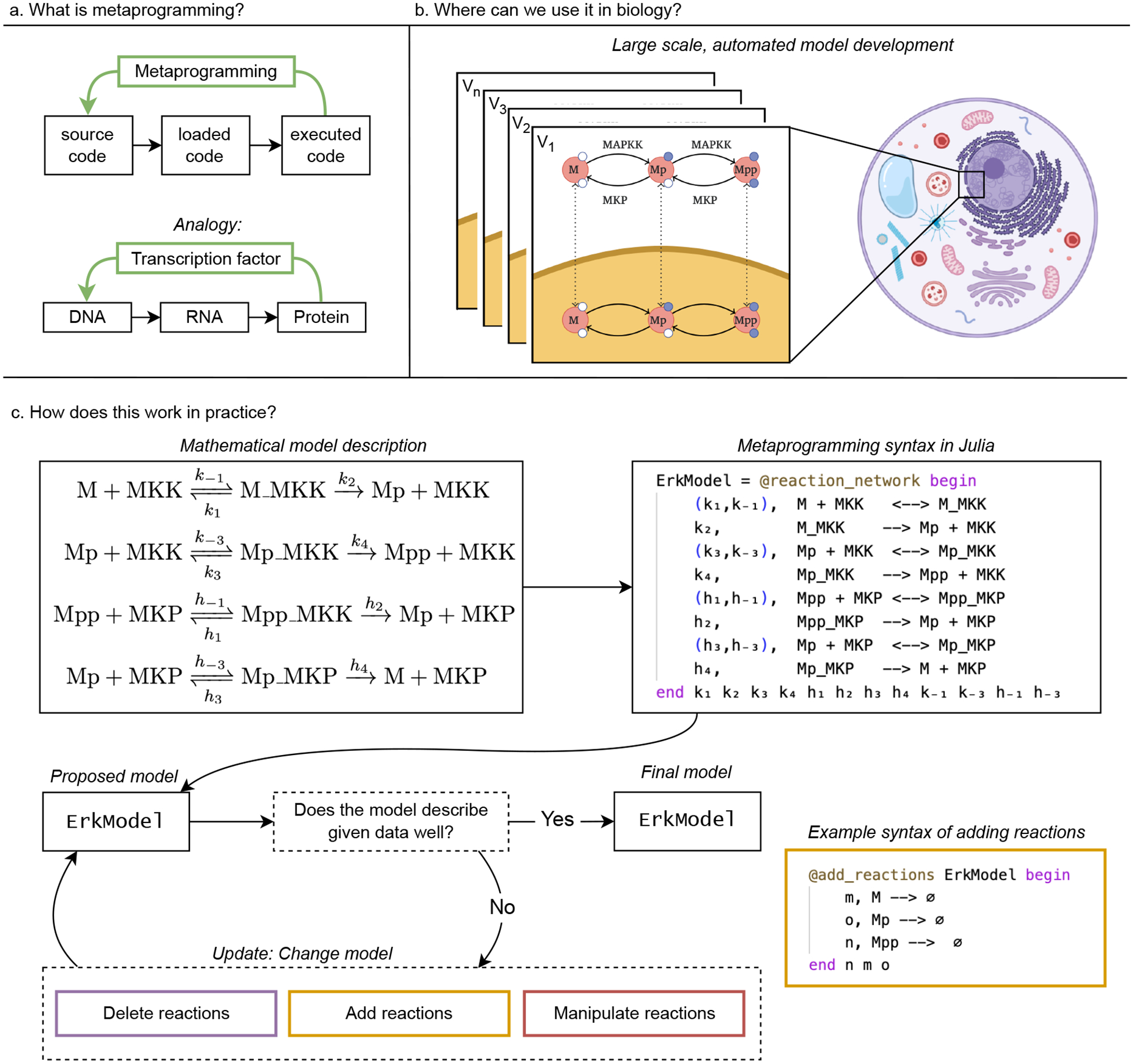
Julia’s Metaprogramming feature. (a) Illustration of metaprogramming and an analogy to the central dogma of molecular biology. Similar to how a transcription factor, initially encoded in DNA, can control gene expression and modify RNA levels of an organism, with metaprogramming we can create code with feedback effect. (b) Example application of metagprogramming in biology. Metaprogramming is especially helpful for large scale, automated model development. We can write code that adapts the model definition automatically e.g. in light of new data or based on how they interact with other sub-models (V₁, …, V_n: the different versions of the model definition). For example when constructing models of cellular systems we can combined structurally similar models for the different MAP kinases present in human cells, and build compartmental models by explicitly modelling the kinase dynamics in the nucleus and the cytosol [50]. (c) Example workflow of model construction. The adaption process of models could for example start with a theoretical inferred mathematical description, captured via the @reaction_network syntax of the Julia package Catalyst.jl. Subsequently, given experimental data, we evaluate an objective function of the current model capturing the descriptiveness of the model in light of the data. Depending on the outcome of this evaluation, the model will be updated, e.g. via adding new reactions to the model via the macro @add_reactions. More details on the selected example code is in the referenced online material^V.

Metaprogramming originated in the LISP programming language, in the early days of artificial intelligence research. It enables a form of reflection and learning by the software, but the ability of a program to modify computer code needs to be channelled very carefully. In Julia, this is done via a feature called hygenic macros [48]. These are flexible code templates, specified in the program, that can be manipulated at execution time. They are called “hygenic” because they prohibit accidentally using variable names (and thus memory locations) that are defined and used elsewhere. These macros can be used to generate repetitive code efficiently and effectively.

But there are other uses that can enable new research, and this includes the development of mathematical models of biological systems. Unlike in physics, first principles (conservation of energy, momentum, etc.) offer little guidance as to how we should construct models of biological processes and systems. For these notoriously complicated biological systems, trial and error, coupled to biological domain expertise, and state-of-the-art statistical model selection are required [49]. Great manual effort is spent on the formulation of mathematical models, the exploration of their behavior, and their adaptation in light of comparisons to data. Metaprogramming, or the abilities of introspection and reflection during runtime [48], and the ability to automate parts of the modeling process opens up enormous scope for new approaches to modeling biological systems (Figure 6(b)), including whole cells (see Supplementary material).

Example: Biochemical reaction networks.

Mathematical models of biochemical reaction networks allow us to analyze biological processes and make sense of the bewilderingly complex systems underlying cellular function [51, 52, 53]. But the specification of mathematical models is challenging and requires us to specify all of our assumptions explicitly. We then have to solve these models based on these assumption. Analysing a given reaction network can involve solution, for example, of ordinary differential equations (ODEs), delay differential equations, stochastic differential equations (SDEs), or discrete-time stochastic processes. To create instances of each of these models would typically – in languages such as C/C++ or Python – require writing different snippets of code for each modelling framework. In Julia, via metaprogamming, different models can be generated automatically from a single block of code. This simplifies workflows and makes them more efficient, but also removes the possibility of errors due to model inconsistencies.

For example, we can consider the ERK phosphorylation process shown in Figure 6(b) [54]. Here ERK is doubly phosoporylated (by its cognisant kinase, MEK), upon which it can shuttle into the nucleus and initiate changes in gene expression. Its role and importance have made ERK a target of extensive further analysis, and modelling has helped to shed light on its function and role in cell-fate decision making systems [55]. This small system – albeit one of great importance and subtlety – forms a building blocks for larger, more realistic biochemical reaction [51] and signal transduction [56] models.

In Julia, using Catalyst.jl [57], this model can be written directly in terms of its reactions, with the corresponding rates {k₁, k₂, k₃}: source code is human readable and differs minimally from the conventional chemical reaction systems shown in Figure 6(c).

The science is encapsulated in this little snippet; solving the reaction systems then proceeds by calling the appropriate simulation tool from DifferentialEquations.jl: for a deterministic model specified the reaction network is directly converted into a system of ODEs (via ODESystem). The same reaction network can be directly converted into a model that is specified by SDEs (via SDEProblem) or a discrete-time stochastic process model (via DiscreteProblem). Each of these cases leads to the creation of a distinct model that can be simulated or analyzed; yet all of the models share the underlying structure of the same reaction network. To simulate one of the resulting models, the user needs to specify only the necessary assumptions required for a simulation – i.e. the parameter values and initial conditions – as well as any further assumptions required that are specific to the model type, e.g. the choice of noise model for a system of SDEs. Adapting the model to include nuclear shuttling [50] of ERK as in Figure 6(c), or extrinsic noise upstream of ERK [54] is easily achieved using metaprogramming.

Fitting models to data, or estimating their parameters, is also supported by the Julia package ecosystem. Parameter estimation by optimizing the likelihood, posterior or a cost-function is straightforward using the Optim.jl [58] or JuMP.jl [59] packages. And because of Julia’s speed it has become much easier to deploy Bayesian inference methods; here, too, metaprogramming helps tools such as the probabilistic programming environment, Turing.jl [60]. Approximate Bayesian computation approaches [61] also benefit from Julia’s speed, abstraction and metaprogramming and are implemented in GpABC.jl [20].

The code for this example can be found under the attached link^VI.

Outlook

Computer languages, like human languages, are diverse and changing to meet new demands. When choosing a programming language we have many choices, but often they reduce to essentially two options: do we want to use a widely used language with everybody else is using? Or do we want to use the best language for our problem? Traditional languages have an enviable track record of success in biological research. A frightening proportion of the internet and the modern information infrastructure probably depends on legacy software that would not pass modern quality control. But it does the job, for the moment. Similarly, scientific progress is possible with legacy software. Python, R are far from legacy and have plenty of life in them. And there are tools, which allow us to overcome their intrinsic slowness [62].

Here we have tried to explain why we consider Julia a language for the next chapter in the quantitative and computational life-sciences. Julia was designed to meet current and future demands of scientific and data-intensive computing [63]. It is an unequivocally modern language, and it does not have the ballast of a long track record going all the way to the pre-big-data days. The deliberate choices made by the developers furthermore make it fast and give developers and users of the language a level of flexibility that is difficult to achieve in other common languages such as R, Python, but also C/C++ and Fortran. On top of all of that is a state-of-the-art package manager; all packages and Julia itself are maintained via Git, which makes installing and updating the Julia language, packages and their dependencies straightforward [6].

Julia has a growing but still smaller user base than R and Python, and in some domains these languages have truly impressive package ecosystems. R and the associated Bioconductor project, in particular, have been instrumental in bringing sophisticated bioinformatics, data analysis and visualisation methods to biologists. For many they have also served as a gateway into programming. In other application areas, notably simulation of dynamical systems, Julia has leapfrogged the competition [64]. Many of the speed-advantages of Julia come from just-in-time compilation, which underlies and enables good run-time performance. This, however, takes time and causes what is known as latency. Latency can be a problem for applications with hard real-time constraints, such as being the embedded code on a medical device that requires strict accurate updates at 100ms intervals.

Julia was designed to meet current and future demands of scientific and data-intensive computing. The Julia alternative, which arguably has the most traction is Rust. Rust is emerging language that has syntactic similarity to C++ but is better at managing memory safely: it detects discrepancies of type assignments at compile time and not just at run time as is the case for C/C++. For this reason it is being used in e.g. the Linux kernel; in the biological domain it could become a choice for medical devices (as we can control latency), or bioinformatics servers that would previously have been developed in Java or C/C++.

These advantages of a new language need to be balanced against the convenience of programmers who are able to tap into the collective knowledge of vast user communities. All languages have started small and had to develop user bases. The Julia community is growing, including in the biomedical sciences; and, it appears to be acutely aware of the needs of newcomers to Julia (and underrepresented minorities in the computational sciences more generally [65], see e.g. https://julialang.org/diversity/ for details), which makes the switch to Julia easier [14].

We have described the three main language design features that make Julia interesting for the scientific computing: speed, abstraction, and metaprogramming. We have provided some intuition that fills these concepts with life, and we have illustrated how they can be exploited in different biological domains, and how speed, abstraction and metaprogramming, together enable new ways of doing biological research. Even though we have introduced these features separately, they are deeply intertwined. For example, a lot of the speed-up opportunities of Julia derive from the languages abstraction powers; abstraction in turn makes metaprogramming easier.

Figure 3:

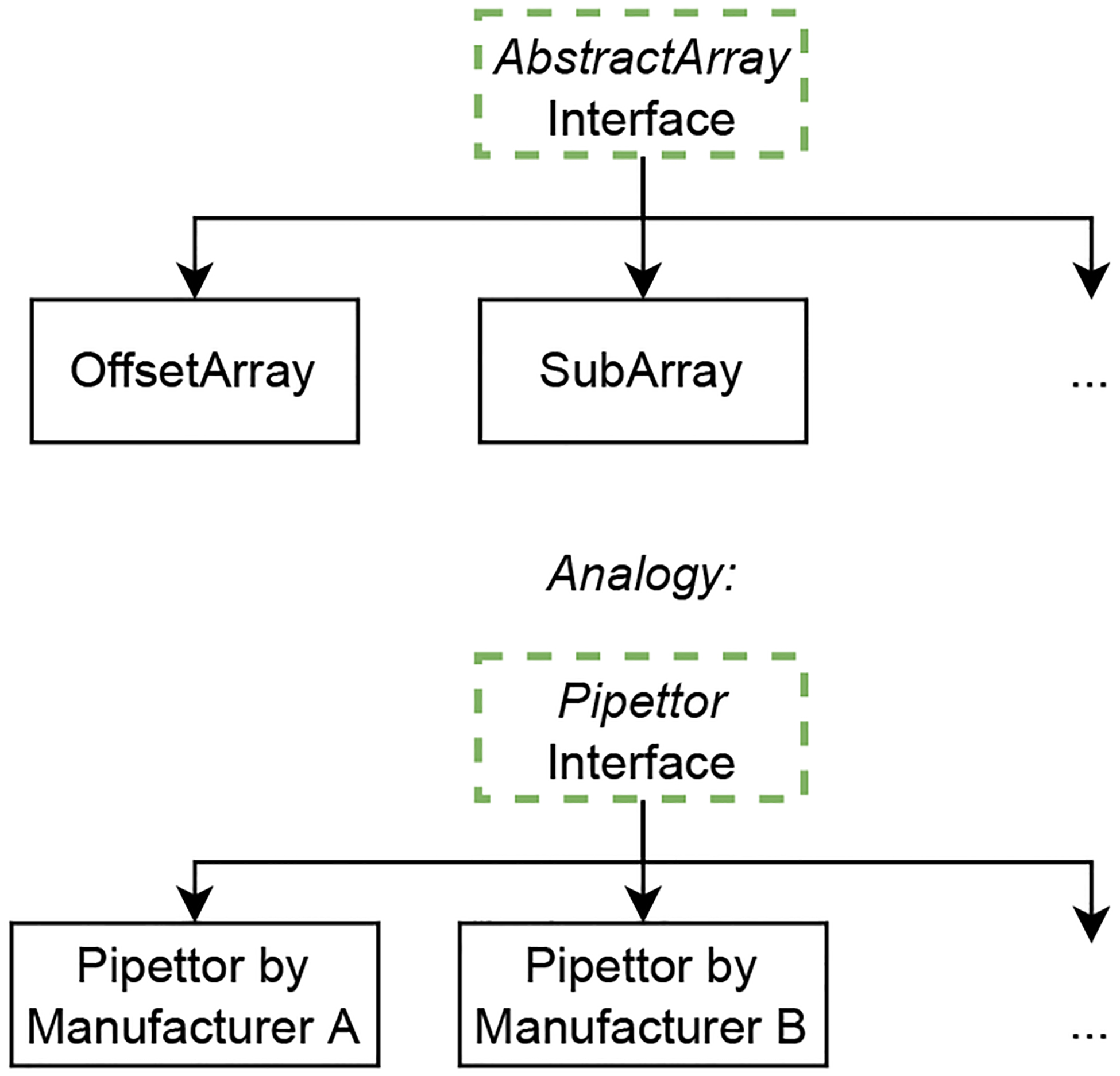
Interfaces in Julia: Switching between different pipettors without recreating whole experimental protocols is possible for experimental scientists because a common understanding, or interface, exists that specifies tasks which pipettors should be able to perform in a similar manner. In Julia, we can define interfaces such as the AbstractArray class where we specify rules any array-like computational object has to follow. Interfaces allow us to share methods developed for abstract types to custom types. By building our algorithms around interfaces we can make use, reuse, and refinement of code easier.

Figure 4:

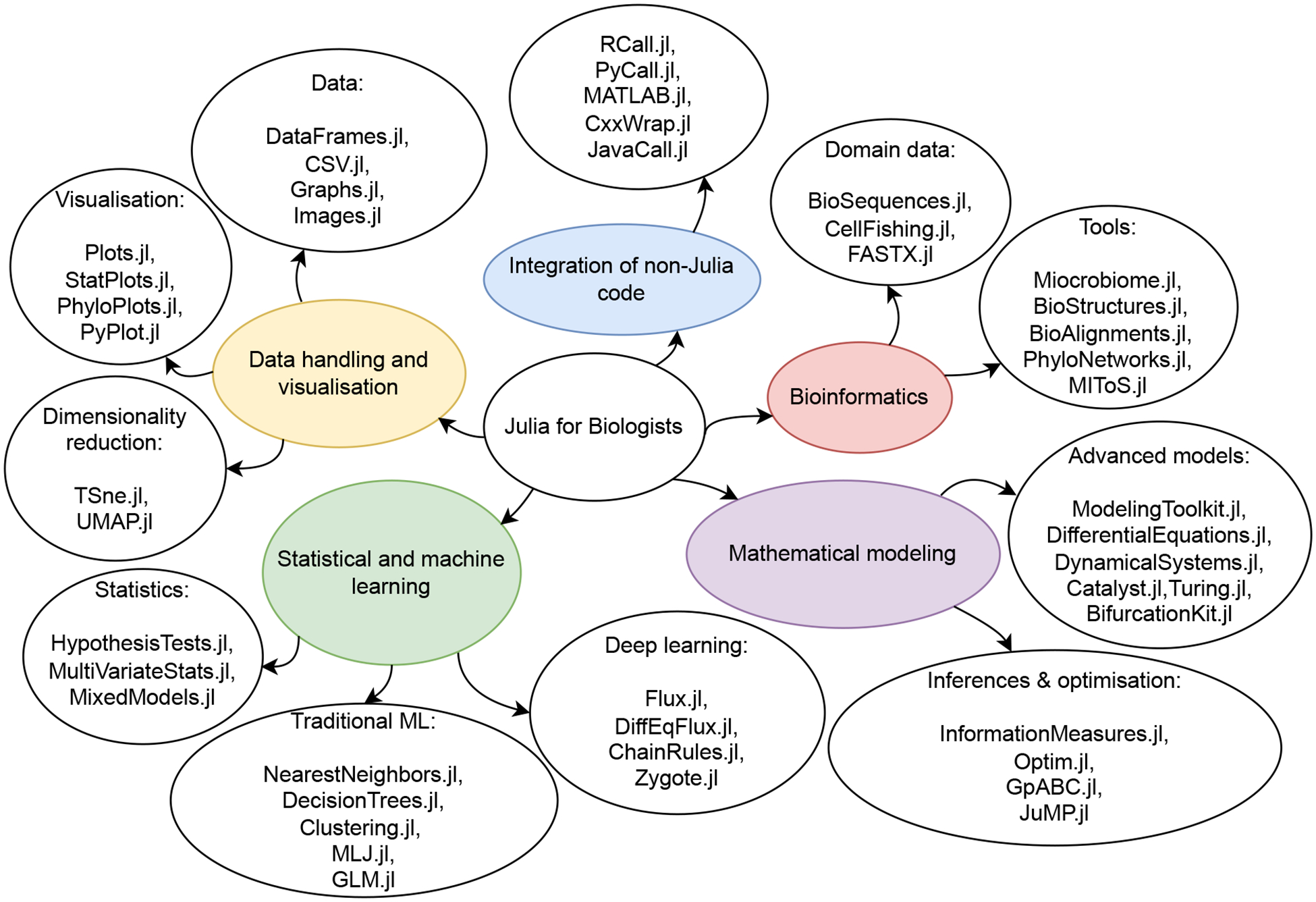
An overview of Julia’s package ecosystem presented by topic groups.

Figure 7:

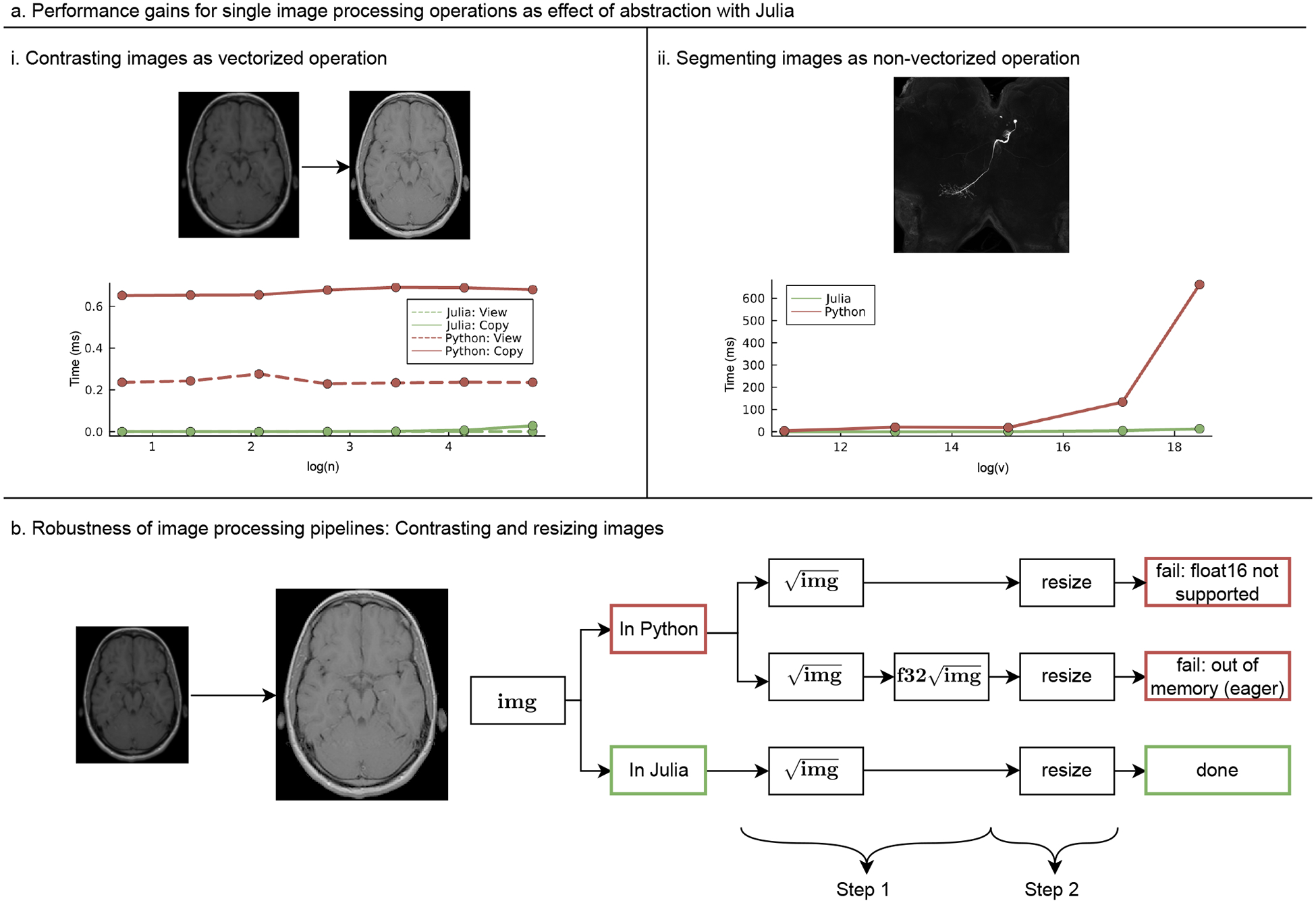
Julia’s Abstraction feature and performance gains in image processing: We demonstrate (a) contrasting (i) and segmenting (ii) images as examples for high performance vectorizable (i) and non-vectorizable (ii) image manipulations, respectively. Performance comparison with Python is provided (ms: millisecond, v: voxel, n: n x n patch of array).(b) Example of robustness in image processing via a 2-step image processing pipeline on contrasting and resizing of images in Julia and Python. For more details see the README.md document under https://github.com/ElisabethRoesch/Perspective_Julia_for_Biologists/blob/main/examples/Abstraction/Supplementary_Example_Flexibility_and_performance_in_image_processing/images_lazy.

Table 1:

Julia provides a rich package ecosystem for biologists. Related packages are organised in package communities. In this table, we present an overview of package communities we consider most relevant to biologists.

Community	Topic	Example packages
JuliaData	Data manipulation, storage, and I/O	DataFrames.jl, JuliaDB.jl, DataFramesMeta.jl, CSV.jl
JuliaPlots	Data visualization	Plots.jl, Makie.jl, StatsPlots.jl, PlotlyJS.jl
JuliaStats	Statistics and Machine Learning	Distributions.jl, GLM.jl, StatsBase.jl, Distances.jl, MixedModels.jl, TimeSeries.jl, Clustering.jl, MultivariateStats.jl, HypothesisTests.jl.
BioJulia	Bioinformatics and Computational Biology	BioSequences.jl, BioStructures.jl, BioAlignments.jl, FASTX.jl, Microbiome.jl
Julialmages	Image processing	Images.jl, ImageSegmentation.jl, ImageTransformations.jl, ImageView.jl
EcoJulia	Ecological research	SpatialEcology.jl, EcologicalNetworks.jl, Phylo.jl, Diversity.jl
SciML	Scientific machine learning	DifferentialEquations.jl, ModelingToolkit.jl, DiffEqFlux.jl, Catalyst.jl
FluxML	Machine Learning	Flux.jl, Zygote.jl, MacroTools.jl, GeometricFlux.jl, Metalhead.jl

Appendix

Here we provide supplementary material related to the main manuscript. This includes a table outlining advantages and resources that ease the transition to the Julia language (Table 2); an illustration of Julia’s speed in the context of quantitative systems pharmacology; a discussion of Julia’s abstraction capability in the context of image processing; an outline of the advantages Julia’s metaprogramming capabilities offer to efforts to model whole cells.

Speed

Supplementary Example: Accelerating Dynamical Systems Modeling in Systems Biology and Pharmacology.

Systems biology and related fields, including quantitative systems pharmacology (QSP), are also benefiting from Julia’s speed. Modeling and simulation are transforming the drug discovery pipeline, lowering the risk of failed trials, and allowing efficiency gains in drug development and substantial financial savings in the drug development process [66]. However, even with these successes most trials do not undergo in-depth preclinical analysis. The major reason why is time: any delay in the start of the clinical trial increases the overall cost. Improvements in QSP can remedy this situation.

Solving large systems of ordinary differential equations (ODEs) (and increasingly also stochastic dynamical systems) lies at the core of these modelling studies. We typically have nonlinear functions, f, and solving them in high-level languages such as R, Python or Matlab can be slow. Therefore solver libraries are often written in a faster language, such as C/C++ or Fortran. The limiting factor then is the user’s non-linear set of equations, f. In languages like Python or R, there is a high function call overhead: every operation that is called is more expensive than in a fast language (approximately 150–350ns per call [67] while the function calls can take approximately 5ns in Julia or C). Scalar operations, like evaluating a Hill kinetic function $[A]\prime =\frac{{[B]}^n}{\omega +{[B]}^n}$, can take microseconds instead of nanoseconds, see Figure 2. “Vectorization”, as recommended in languages such as Python or R, packs more floating point operations into each C function call and can help to speed this up somewhat. Even accelerators like Numba still require a context change from Python to the compiled C function, which can hamper performance, especially for sparse reaction networks. Furthermore, vectorization requires a certain level of regularity and simplicity in the equations, and the nonlinear systems typically found in biology can be anything but simple; therefore traditional interpreted languages will always tend to perform poorly for nonlinear models.

When solving an ODE, the function f is called thousands or millions of times, exacerbating this difference. Figure 2 showcases some examples of biological models where such simulations are 50x-400x faster than those using leading packages in R and Python. In a typical preclinical drug development pipeline this has led to 175-fold acceleration of QSP model analysis once the model had been translated from a combination of MATLAB and C code into Julia [68]. Julia’s speed enables more efficient clinical trial analyses and its libraries have been shown to be even faster than commonly used Fortran libraries in this domain of ODE modeling [64].

The code for this example can be found under the attached link^VII.

Abstraction

Supplementary Example: Flexibility and performance in image processing.

Microscopy in its many forms underlies much of modern biology. But extracting information from imaging data is challenging for two main reasons. The first challenge lies in the nature of the raw data. Scientific images can be very large, and it is not uncommon for datasets to reach a size of multiple terabytes [69, 70]. In such instances, initially minor performance inconveniences can quickly extrapolate to become limiting factors for scientific discovery. Also, the images – typically internally represented as arrays – often exhibit great diversity: for example, a single imaging dataset may have two or three spatial dimensions, zero or one temporal dimensions, and a color- or modality-channel. This is further exacerbated by the complexity of the accompanying meta information on the imaging conditions and technologies which also influence down stream analysis and interpretation. Having the flexibility to accommodate for this level of diversity whilst also providing the necessary performance needed when dealing with data of this size, is a non-trivial challenge for any programming language with significant implications for outcomes [71, 72].

The second reason for carefully thinking about the choice of software for image processing pipelines, lies in the nature of processing pipelines themselves. Typically the data are sequentially manipulated over multiple steps. In a naive approach, a new, slightly altered version of the large raw dataset is created and stored for each step in the pipeline. This is inherently inefficient and becomes quickly infeasible or impossible as data sizes grow beyond storage capacities. Documenting and tracking different combinations of data manipulation steps is also non-trivial as each step could lose information.

Efficient data representation combined with flexible processing is of essence to extract meaningful conclusions from the data. Abstraction is Julia’s key feature that enables state-of-the-art image processing [73, 74]: by keeping a high level of abstraction in the internal data representations, the diversity in image data can be captured and exploited, and modifications to the data become easier, too. A core component for implementing the relevant abstraction in Julia is provided by the AbstractArray interface [75], especially in its combination with lazy operations. In a normal, “eager”, operation, each computation is executed immediately upon being invoked. By contrast, lazy operations delay their computations until the latest possible moment in time, i.e. the execution is separated from the declaration of a computation. In some cases, this can be delayed all the way to the moment where we wish to visualize the processed data, so that no computation needs to occur on any data not being inspected.

As previously described, the AbstractArray interface can be thought of as a template which creates an agreement between existing software and the user’s software. We can use the template, i.e. implement the AbstractArray interface, in order to define a new array type which optimally fits their data format. By using the interface, we also agree to provide certain functionalities for this new object. Providing both high levels of customization and standardization of operations that need to be supported by an array-like object, allows for the composition of complex and highly specialised pipelines. The specifics of the array no longer matter because of the abstraction. Many AbstractArray interface implementations helpful in image processing already exist and we do not have to start from scratch for each new imaging modality. Examples include SubArrays (region-of-interest “view” selection), MappedArrays (lazy-modification of values), “ReshapedArrays” (lazy-modification of dimensionality), and WarpedViews in the ImageTransformations.jl package (lazy coordinate transformations).

With effective lazy operations, it becomes possible to manipulate and inspect massive datasets even with relatively modest computing hardware, because the hardware only needs to load, process, and display the small subset of the data being actively explored. Preprocessing stages that might require tuning several parameters to the particulars of the dataset can be refined quickly, with each iteration perhaps comprising only a few seconds or minutes, rather than the hours, days, or weeks that might be required if each step had to cached to disk between manipulations.

Other languages support the concepts of abstraction and lazy operations, too, but despite considerable investment they do not provide the same level of comfort and capability available in Julia. For example, in Python, the most widely-used lazy-operation package is Dask [76], which has a sophisticated engine for managing computational graphs and applying them across distributed datasets. However, when using Dask to process large image datasets, one frequently encounters severe limitations on composability (Figure 5.c): some algorithms may not support outputs of previous stages, while others may force an eager intermediate step in the pipeline potentially exhausting memory resources, and yet others may attempt to allocate an unachievable output array. By contrast, with Julia, one can routinely expect that arbitrary combinations of processing “just work” together, and we can use lazy operations along the whole image processing pipeline. Because Julia aggressively optimizes computations at a granular level (all the way to the single pixel), this flexibility comes with little or no overhead, in marked contrast to languages such as Python (Figure 5.a and additional information in the accompanying Repository 1).

Figure 5:

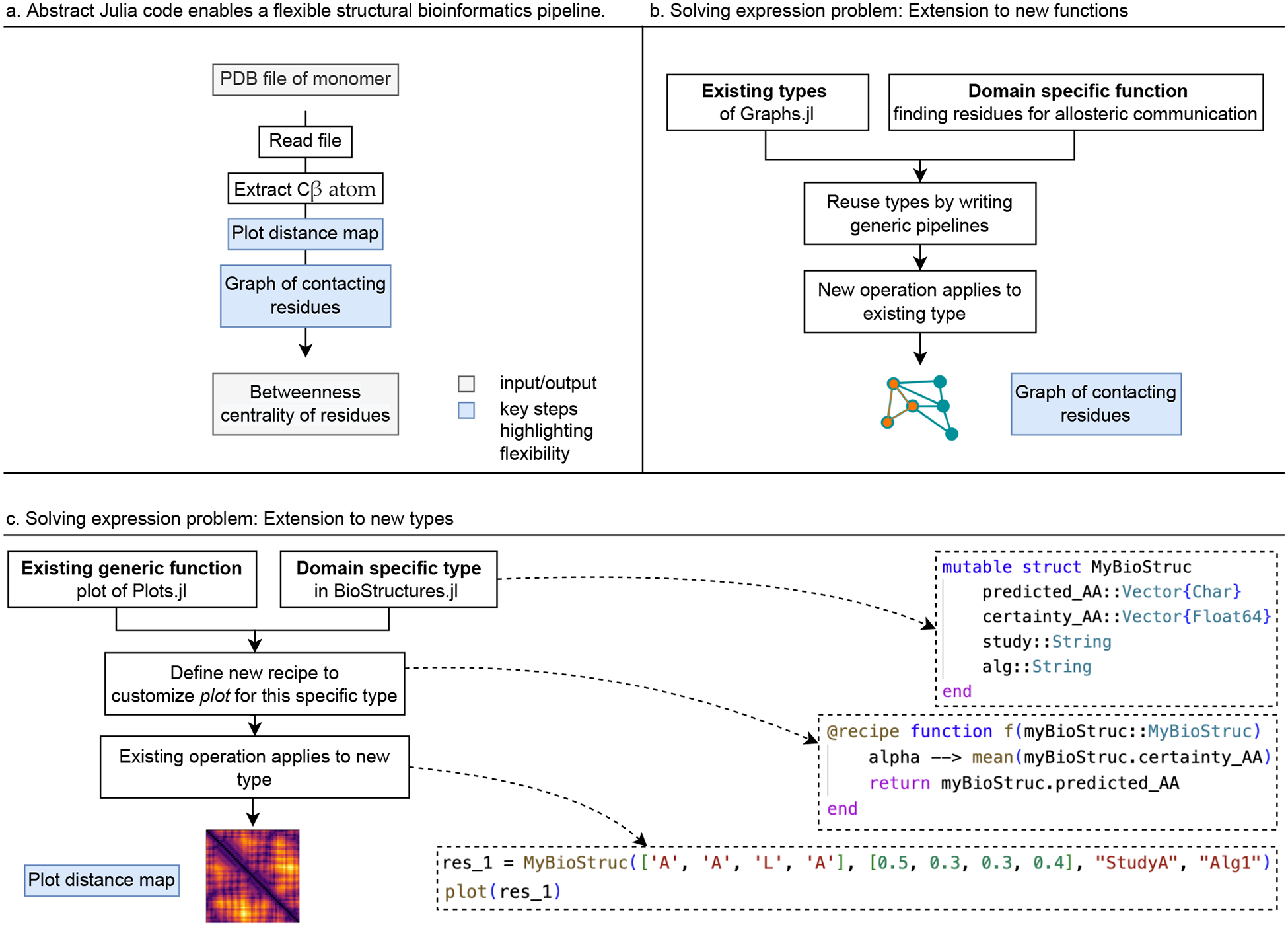
The abstraction feature in Julia. (a) We show a structural bioinformatics pipeline which combines multiple Julia packages seamlessly together. This gives developers and users the flexibility is that the effort and time to generate new models and complex workflows is significantly reduced and collaboration is made easier. (b) From the pipeline, we highlight the step “Graph of contacting residues” as an example of Julia’s solution to the first part of the expression problem (Illustration of expression problem in Figure 1) which is the easy code base extension to new functions. (c) The second highlighted step from the pipeline is “Plot distance map” where a new plot recipe is defined for a domain specific type, i.e. we demonstrate the extension of an existing code base to new types. Along this, we show the Julia code for defining a new type and and a new plot recipe: As an example, this is the structure MyBioStruc which captures results of prediction algorithms of amino acid (AA) sequences based on data. It is defined with the fields predicted_AA a vector of characters which are the predicted AAs, certainty_AA a vector of numbers, quantifying the certainty for each predicted AA, the string study naming the respective data study the prediction is based on and the string alg naming the respective prediction algorithm. With the macro @recipe we can specify how the function plot(…) should work for our newly specified example type. Here, we define that this should create a line plot of the predicted amino acids with the mean of the certainty of the prediction as opacity of the line specified by the Plots.jl package as α More details on the selected example code is in this referenced online material^IV.

The objective of the software as a tool in the instance of image processing should be to provide the adequate level of flexibility a biologist needs in order to discover new science without being limited by data storage and performance issues caused by the software. Julia and its high level of abstraction provides this flexibility to biologists and therefore enables new analyses and experiments. For example, Julia has previously been adopted by labs processing large images acquired by light sheet microscopy in mice [73] and fish [70]. Julia also enabled a real-time two-photon pipeline to perform calcium imaging in intact neural tissue and then select and phototag specific cells that exhibited specific response properties [73].

The code for this example can be found under the attached link^VIII.

Metaprogramming

Supplementary Example: Whole cell modeling.

An additional application area for metaprogramming is the development of physiologically more realistic models, whether at the levels of whole cells, tissues, or even the physiology of whole organisms. In whole cell modeling, models potentially scale up to the size of 10³–10⁵ species [77] and a key problem is that constructing models of this size is extremely difficult [78, 79]. In fact even small parts of such models, see Figure 6, such as signalling cascades have a large number of (generally unknown) parameters. Here model development cannot rely on manual curation or inspired guesswork [78]. Instead automated model development will be required [77]. The reasons for this is that the bookkeeping efforts required to keep track of molecular species, their interactions, and the ways in which molecule numbers change as a result of biochemical interactions, are simply not manageable by conventional means. We do not know the model structure and therefore have to experiment with different model-setups. Without metaprogramming we would have to write or adapt the cellular simulation code for each new attempt. Plus, of course, nobody is able to check the validity of such a large model in the way we can check a simple mathematical model of the type that has traditionally dominated theoretical biology.

Developing a whole cell model will almost certainly involve piecing together sub-models, for which we can build on Catalyst.jl [57]. Calibrating such (sub-) models against data – that is to infer parameters from data – is a demanding task, that has yet to be solved for such large systems (it is a priori not clear to what extent this can be solved). Approximations to the dynamics and/or the inference process can help; and for many sufficiently small systems (say signalling networks) current tools will allow us to determine their parameters from literature and/or data, as described in the example above. We may, in addition, want to use efficient approximations to the stochastic dynamics [80, 81], such as provided by MomentClosures.jl [82]. This can be coupled to parameter inference, as described above, via optimization (Jump.jl [59]) or Bayesian inference (Turing.jl [60] and GpABC.jl [20]).

Catlab.jl is a package that makes composing and combining smaller models into a larger model possible, and relatively straightforward. The toolset that we can use to construct such models continues to grow. For example, hypergraphs provide a much more flexible representation for mathematical models that conventional networks, and For such comprehensive models, grown in a principled way, the SciML suite, via e.g. SciMLSensitivity.jl [83], allows us to quantity uncertainty and assess sensitivity of model outputs both locally and globally. Metaprogramming alleviates the need to “hard-code” such large models. Instead they can be generated automatically without sacrificing the runtime efficiency of the simulation models.

The model development process enabled by the pipeline, Sub-model formulation → Sub-model fitting → Composition of Large Model from Sub-models → Sensitivity and Uncertainty Analysis,

Overall, metaprogramming in Julia enables the automated construction of models of all sizes: from small biochemical reaction network models to whole cell models. Simulation, inference, and analysis of these models can all be performed with great paucity of code, reducing opportunities for errors to arise, and greatly enhancing our ability to describe and predict complex biological processes with mathematical models.