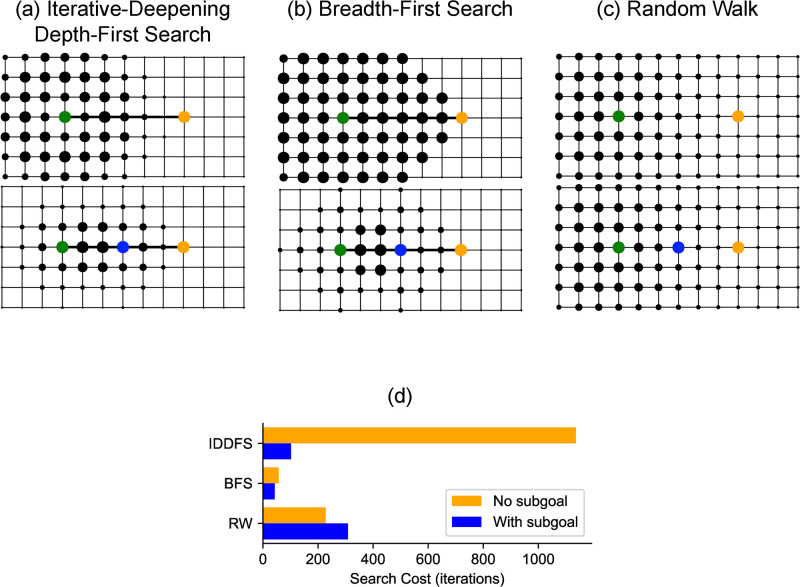
Fig 2. Choosing task decompositions that make planning more efficient.

(a-c) State-specific search costs of the algorithms. The depicted task requires navigating on a grid from the start state (green) to the goal state (orange) with the fewest steps. Each column corresponds to a different algorithm and demonstrates two scenarios—Top: Search cost without subgoals, Bottom: Search cost when using the path midpoint as a subgoal (blue). We define the search cost as the number of iterations required for the search algorithm to find a solution. Larger states were considered more often during the search algorithm, resulting in greater search costs. (d) Plot of search cost for Iterative-Deepening Depth-First Search (IDDFS), Breadth-First Search (BFS), and a Random Walk (RW) in the task depicted in (a-c), with and without subgoals. Use of subgoals results in decreased search cost for BFS and IDDFS, but not for RW.