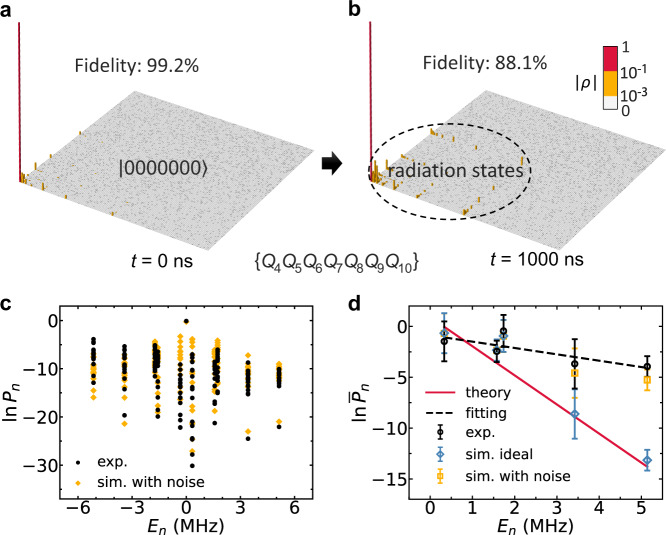
Fig. 3. Observation of analog Hawking radiation.

a The 7-qubit density matrix at t = 0 ns. Initially, only Q₁ is prepared in $∣1⟩$ and all the qubits outside the horizon are almost in $∣0⟩$. b The 7-qubit density matrix at t = 1000 ns after the quench dynamics. Due to the Hawking radiation, radiation states can be detected with small probabilities. The fidelity between ideal and experimental density matrix at t = 0 and 1000 ns are 99.2% and 88.1%, respectively. c The logarithmic probability of finding a particle outside the horizon P_n vs. its energy E_n. d The logarithm of average radiation probability vs. the energy of particle when E_n > 0. Error bars are 1 SD calculated from the tomography data at the same energy. The slope of the red line represents the reciprocal of Hawking temperature without noise, where the Hawking temperature here is given by T_H/(2π) = β/(8π²) ≈ 0.35 MHz or ≈ 1.7 × 10⁻⁵ K in Kelvin temperature. The experimental results are in agreement with the simulated data for low energy but diverge at high energy due to experiment noises.