Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 May 25;8(22):19917–19925. doi: 10.1021/acsomega.3c01875

Computational Analysis of Chemical Reactions Using a Variational Quantum Eigensolver Algorithm without Specifying Spin Multiplicity

Soichi Shirai †,*, Hokuto Iwakiri ‡, Keita Kanno ‡, Takahiro Horiba †, Keita Omiya ‡, Hirotoshi Hirai †, Sho Koh ‡,*
PMCID: PMC10249088  PMID: 37305284

Abstract

graphic file with name ao3c01875_0008.jpg

The analysis of a chemical reaction along the ground-state potential energy surface in conjunction with an unknown spin state is challenging because electronic states must be separately computed several times using different spin multiplicities to find the lowest energy state. However, in principle, the ground state could be obtained with just a single calculation using a quantum computer without specifying the spin multiplicity in advance. In the present work, ground-state potential energy curves for PtCO were calculated as a proof-of-concept using a variational quantum eigensolver (VQE) algorithm. This system exhibits a singlet–triplet crossover as a consequence of the interaction between Pt and CO. VQE calculations using a statevector simulator were found to converge to a singlet state in the bonding region, while a triplet state was obtained at the dissociation limit. Calculations performed using an actual quantum device provided potential energies within ±2 kcal/mol of the simulated energies after error mitigation techniques were adopted. The spin multiplicities in the bonding and dissociation regions could be clearly distinguished even in the case of a small number of shots. The results of this study suggest that quantum computing can be a powerful tool for the analysis of the chemical reactions of systems for which the spin multiplicity of the ground state and variations in this parameter are not known in advance.

Introduction

Issues related to the use of fossil fuels, including the finite nature of these resources and climate change, have become significant on a global scale.1,2 As such, hydrogen production through water splitting and the conversion of carbon dioxide into liquid fuels have attracted much attention.3−5 The development of high-performance catalysts for these processes that contain reduced amounts of noble metals is also required on the basis of economics and sustainability. Quantum chemical calculations are now routinely used to simulate various reactions in conjunction with experimentation to expedite the development of such catalysts by providing an understanding of reaction mechanisms on the molecular level and to assist in material design.

The majority of current industrial catalysts utilize metal or alloy clusters, metal oxides, or metal complexes in which the metals serve as active centers.6,7 Accordingly, the interactions between adsorbed molecules and these metal atoms is a fundamental aspect of the catalytic reactions and must be accurately described to allow reliable simulations. However, distributing many electrons over the multiple orbitals associated with the catalytic centers and the adsorbed molecules results in numerous electronic states that are close in energy as a consequence of the degenerate or nearly degenerate d and f orbitals of the metal atoms. Describing such highly correlated electronic states requires a multiconfiguration treatment based on the configuration interaction (CI) theory8 instead of the more commonly used density functional theory (DFT) methods.

A CI wave function is represented as a linear combination of Slater determinants corresponding to the various electron configurations for a system. In the case of so-called full CI, all of the electron configurations generated from combinations of all of the electrons and orbitals of the system are used.9 Although this approach provides exact wave functions for an adopted basis set, the number of electron configurations (which, in turn, determines the computational load) rapidly increases along with the number of electrons and orbitals such that the load can easily exceed the capacity of standard computers. Consequently, only truncated CI calculations with selected electron configurations are carried out in practice, except for the simplest molecules. For these reasons, the use of quantum computers for quantum chemical calculations has recently attracted much attention.10,11 Quantum computers with qubits have the potential to perform full CI calculations in polynomial time by employing a quantum-phase estimation (QPE) algorithm to estimate the eigenvalues of specific Hamiltonian operators.12−15

In addition to advantages related to reduced computational costs, quantum chemistry calculations performed using quantum computers can also determine electronic ground states without specifying the spin multiplicity in advance. This is helpful because, in the case of certain transition metal catalysts in which the metals serve as active centers, the spin multiplicity of the electronic ground state varies depending on the molecular geometry.16−21 Thus, it is necessary to trace changes in the spin multiplicity along the reaction coordinates when assessing such systems. In contrast, the spin multiplicity must be specified when performing DFT calculations. For this reason, the analysis of a chemical reaction along the ground-state potential energy surface is challenging because it is necessary to compute electronic states several times while specifying different spin multiplicities and to compare the resulting energies to identify the lowest energy state. Conversely, because a superposition of multiple states having different spin multiplicities can be prepared using the qubits of a quantum computer, the ground state can, in principle, be obtained with just a single calculation employing the QPE algorithm if the initial state overlaps significantly with the ground state. As such, it will be possible to trace the reaction path along the ground state even if the spin multiplicity changes along the way without involving complicated operations, unlike the aforementioned calculations performed with conventional computers. Therefore, quantum computers are expected to serve as a useful tool for the analysis of the reactions of a system for which the spin multiplicity of the ground state is not obvious. This computational technique could also be applied to analyses of the ground states of strongly correlated systems having electronic states that are close in energy to the ground state but different in terms of spin multiplicity.22−26 Unfortunately, such QPE calculations require fault tolerance and cannot be executed on current quantum computers having qubits without error correction, generally referred to as noisy intermediate-scale quantum (NISQ) devices.27−29 Accordingly, a quantum-classical hybrid algorithm known as the variational quantum eigensolver (VQE) is widely employed for quantum chemical calculations using NISQ devices.30,31 These VQE calculations solve the ground-state wave function by minimizing a given cost function on the basis of the variational principle. In the case of a VQE scheme, adopting an ansatz describing multiple spin states can allow the ground state to be directly determined by minimizing the cost function.

The present study demonstrates that a reaction path along a ground-state potential energy curve including spin crossover can be traced using quantum algorithms. Specifically, the potential energy curves for the adsorption of a carbon monoxide (CO) molecule on a platinum (Pt) atom were calculated using a VQE algorithm as a proof-of-concept. This adsorption is one of the most extensively studied systems in the fields of surface and catalytic chemistry, and PtCO is the simplest model for this reaction. Prior theoretical studies have suggested that this system has a singlet ground state in its equilibrium geometry32,33 but a triplet state at the dissociation limit because of the triplet ground state of the neutral Pt atom.34 Thus, the ground state of PtCO exhibits spin crossover resulting from the interaction between the Pt and CO. It is worth mentioning that RuCO, RhCO, OsCO, and IrCO systems also exhibit a similar spin crossover in their potential energy curves.35−37 In this work, VQE calculations were used to calculate the ground-state potential energy curves of PtCO, including a singlet–triplet spin crossover, without specifying the spin multiplicity in advance. The spin multiplicity could be estimated efficiently on the basis of a small number of measurements using an actual quantum device even under noisy conditions, implying that the evaluation of discrete values may be a useful application of NISQ devices. The calculations without spin specification have been studied within the conventional ab initio theory for classical computers. Spin-free quantum chemistry38−40 has been investigated as an alternative approach to formalism based on the spin-adapted basis.41 The determinant-based CI calculation can provide solutions having different multiplicity by diagonalizing the CI Hamiltonian; for example, calculation with the Slater determinants with MS = 0 can provide singlet and triplet solutions.41−43 These algorithms allow us to explore the ground state without specifying spin multiplicity in advance. Although the methods for classical computers have been well developed,44 calculations based on quantum algorithms are still in their early stages. This study triggers the application of quantum algorithms for such calculations.

Theory

VQE

The VQE method is a quantum-classical hybrid technique based on the variational principle.30,31 In this process, a trial wave function is constructed using a quantum computer based on the initial wave function |Ψo⟩ and the ansatz quantum circuit Û(θ) with variational parameters θ. The expected value of the molecular Hamiltonian ⟨Ψo|Û†(θ)ĤÛ(θ)|Ψo⟩ is repeatedly determined with a quantum computer, while the variational parameters θ are repeatedly updated using a classical computer so as to minimize the cost function:

graphic file with name ao3c01875_m001.jpg 1

To ensure that the computed wave function has the desired properties, a penalty term is typically included as31,45,46

graphic file with name ao3c01875_m002.jpg 2

In the case of spin multiplicity, Lpenalty is typically written as

graphic file with name ao3c01875_m003.jpg 3

where w is a weighting coefficient that determines the magnitude of the penalty, Ŝ2 is the square of the total spin angular momentum operator, and p is the eigenvalue of Ŝ2 that the wave function should satisfy. Note that the spin multiplicity can be specified by defining p. In contrast, the wave function can be calculated without specifying the spin multiplicity by setting w to zero. This computational scheme was utilized in the present study.

PtCO

This work focused on the low-lying singlet and triplet states of PtCO, either of which could be the ground state. These states could be identified on the basis of the electron configurations of the molecular orbitals derived from the Pt 5d and 6s atomic orbitals. The ground state of a neutral Pt atom is the triplet state, equivalent to the electron configuration (5d)9(6s)1, and this state is denoted herein by the symbol 3D3. The lowest energy singlet state, 1D2, has the same electron configuration as 3D3 but a total spin angular momentum of S = 0. In contrast, the 1S0 state is associated with the closed-shell electron configuration (5d)10(6s)0. The electron configurations of these states are illustrated in Figure 1. The energy levels of these states increase in the order of 3D3 < 1D2 < 1S0. The 6s orbital of Pt contacts and stabilizes because of the relativistic effect, which is responsible for making the ground state 3D3 with the electron configuration of (5d)9(6s)1.47 Thus, the ground state of PtCO at the dissociation limit is a triplet state derived from the 3D3 state of Pt, and all five d orbitals have the same energy. However, in the case of the PtCO model, the degeneracy of the 5d orbitals is removed as a result of interactions with the CO molecule. Assuming that PtCO has a linear structure, as previously suggested by a DFT study performed by Wu et al.,33 the Pt 5d orbitals will be split into three energy levels as shown in Figure 2. The energy gap between the Pt 6s orbital and the highest Pt 5d orbital is therefore increased by the presence of the CO. In the case that the energy gap between the Pt 5d and 6s orbitals is greater than the value for the exchange interaction, a closed-shell singlet state having a (5d)10(6s)0 configuration becomes energetically preferable to the triplet state with a (5d)9(6s)1 configuration. Therefore, the ground state of PtCO can comprise a closed-shell singlet state in the case that the Pt and CO are in close proximity to one another.

Figure 1.

Figure 1

Open in a new tab

Diagrams showing the electron configurations associated with the (a) 3D3, (b) 1D2, and (c) 1S0 states of a neutral Pt atom.

Figure 2.

Figure 2

Open in a new tab

Diagrams showing the alignments of the molecular orbitals of PtCO derived from Pt 5d and 6s atomic orbitals for the (a) dissociation limit and (b) bonding region. A PtCO molecule that is linear along its z-axis is assumed.

Computational Details

Conventional quantum chemical calculations were initially performed to determine the computational procedure and conditions required for the VQE calculations. Subsequent to this, VQE calculations were performed using both a simulator and a quantum device to demonstrate that the ground state could be determined without specifying the spin multiplicity. In preparation for these calculations, the geometry of the PtCO molecular structural was optimized using the DFT method with the B3LYP functional48−51 together with the def2-QZVP basis set for the Pt atom52 and the cc-pVQZ basis set for the C and O atoms.53 The Gaussian 16 program was employed for these calculations,54 and a linear-structured PtCO with an r(C–O) value of 1.1446 Å was obtained. Note that, herein, r(X–A) represents the interatomic distance between atoms X and A. The r(C–O) distance was fixed at this value in the following calculations. Plots of potential energy as a function of r(Pt–C) were generated over the r(Pt–C) range of 1.55–5.0 Å. In these calculations, the linear PtCO molecule was placed on the z-axis, and C2v symmetry was applied. Accordingly, the symmetries of the dxy, dyz, dxz, dx2–y2, and dz2 orbitals were a2, b2, b1, a1, and a1, respectively, while that of the molecular orbital derived from Pt 6s was a1. Because a closed-shell singlet state has A1 symmetry, those electronic states having A1 symmetry were investigated in this study. It should also be noted that spin–orbit (SO) interactions were not incorporated into the calculations. SO interactions typically have significant effects on the electronic states of the systems that include heavy elements such as Pt. Considering SO coupling, the molecular symmetry should be treated in the framework of double group.55,56 Providing that SO coupling is incorporated, the electronic states of the PtCO system can be correctly described. Nevertheless, considering SO coupling is computationally demanding. In the present work, a qualitative description of the spin crossover was sufficient to allow the applicability of the quantum algorithm without specifying the spin multiplicity to these calculations to be ascertained. Henceforth, the electronic states of Pt treated in this study are denoted by 3D, 1D, and 1S. Meanwhile, we adopted a basis set with the effective core potential (ECP) for Pt,52 meaning that the scalar relativistic effects were considered at the ECP level.

Calculations with Conventional Methods

The potential energy curves for PtCO were calculated using the complete active space self-consistent field (CASSCF) method57,58 and the complete active space configuration interaction (CASCI) method.59 The former approach is widely used to determine electronic states associated with multiple electron configurations. In CASSCF calculations, the molecular orbitals and the expansion coefficients of electron configurations are both optimized for the target state. Calculations at the same level of theory can be performed within the VQE framework by adopting an orbital optimization scheme (OO-VQE),60,61 although this requires a huge number of calculations because of the iterations involved in the VQE process, leading to a high computational cost. Therefore, the present work did not employ the orbital optimization technique. The accuracy of the CASCI calculations was also examined on the basis of a comparison with the CASSCF results. The present CASSCF and CASCI calculations were carried out using the GAMESS program.62,63

CASSCF Calculations

The accuracy of the CASSCF calculations depends on the construction of the active space, and this work employed the CAS(10e, 6o), CAS(4e, 3o), and CAS(2e, 2o) active spaces. Herein, the CAS is denoted as CAS(Me, No) on the basis of the numbers of active electrons M and of active orbitals N. The CAS(10e, 6o) space was constructed by distributing 10 electrons over six molecular orbitals derived from Pt 5d and 6s atomic orbitals. The CAS(4e, 3o) space was constructed by distributing four electrons over three orbitals having a1 symmetry selected from the active orbitals of the CAS(10e, 6o) space. Finally, the CAS(2e, 2o) space was obtained by selecting the two highest energy orbitals from the active orbitals of the CAS(4e, 3o) space. The three lowest energy singlet states and the two lowest energy triplet states having A1 symmetry were evaluated in the calculations on the basis of the CAS(10e, 6o) and CAS(4e, 3o) active spaces. Henceforth, these states are denoted as 11A1, 21A1, 31A1, 13A1, and 23A1. When using the CAS(2e, 2o) space, the two lowest energy singlet states and the lowest triplet state were calculated. The basis sets were def2-QZVP for the Pt atom and cc-pVQZ for the C and O atoms.

CASCI Calculations

The potential energy curves for PtCO associated with the two lowest energy singlet states and the lowest triplet state were calculated using the CASCI method with the CAS(2e, 2o) space. It should be noted that the results were dependent on the molecular orbitals that were considered because orbital optimization was neglected. Restricted Hartree–Fock (RHF) orbitals and restricted open-shell HF (ROHF) orbitals were both examined. The ROHF orbitals were obtained for the lowest energy triplet state, 13A1. The effects of the basis set were also evaluated, employing the def2-SVP, def2-TZVP, and def2-QZVP basis sets for the Pt atom52 combined with the cc-VDZ, cc-pVTZ, and cc-pVQZ basis sets for the C and O atoms,53 respectively.

VQE Calculations Using a Simulator and a Quantum Device

The potential energy curves and the total spin angular momentum values for PtCO were calculated using the VQE method without penalty terms, employing both the Qiskit simulator64 and the IBM ibm_canberra quantum device.65 The basis sets used were def2-SVP for the Pt atom and cc-pVDZ for the C and O atoms. The molecular orbitals were prepared using the ROHF method implemented in PySCF.66 The same active orbitals together with the CAS(2e, 2o) state as used in the CASCI calculations were adopted. Parity transformation was used to map the wave function to qubits and reduce two qubits based on parity conservation of the electron number of α spin and the total electron number. As shown in Figure 3, a hardware-efficient ansatz67 omitting Rz gates with a single depth was applied to the computational basis |00⟩ to describe the target wave function in real space. The variational parameters θi (i = 0, 1, 2, 3) for the Ry gates, starting from random initial numbers, were optimized using the Nakanishi–Fujii–Todo (NFT) optimizer.68

Figure 3.

Figure 3

Open in a new tab

A diagram of the present ansatz consisting of Ry rotation gates and a CZ entanglement gate. The computational basis |00⟩ was employed as the initial state, and four variational parameters θi (i = 0, 1, 2, 3) for the Ry rotation gates were optimized during the VQE calculations.

Simulator calculations were carried out to ascertain whether the VQE algorithm itself could provide the ground state without specifying the spin multiplicity. The noise effect was ignored, and the potential energy and total spin angular momentum with statevector were calculated using conventional computers. In the case of those calculations using the ibm_canberra machine, the potential energy and total spin angular momentum of PtCO at r(Pt–C) values of 1.846 and 3.0 Å were determined through the Qiskit Runtime.65 The r(Pt–C) distance of 1.846 Å was chosen because the ground-state potential energy curve was found to exhibit its minimum at this point, whereas 3.0 Å was selected as a typical bond length for a triplet ground state. Three VQE calculations were performed for each molecular structure with a maximum of five iterations for the VQE optimization so as to reduce the computational cost. The Hamiltonian operator was decomposed into seven Pauli operators that were then placed into four groups using a bitwise grouping technique31 to reduce the number of measurements. These measurements were performed using 5008 shots for each group of Pauli operators to ascertain energies during the VQE process. The square of the total spin angular momentum operator Ŝ2, which consists of the three Pauli operators to be determined, was ascertained for the optimized state, employing 16 shots for each group. The twirled readout error extinction (T-REx) method69 implemented in the IBM Qiskit Runtime was adopted to reduce the readout noise effect.

Results and Discussion

CASSCF and CASCI Calculations

The total energies calculated for the electronic states are summarized in Tables S1–S5. The potential energy curves obtained using the CASSCF method with the CAS(10e, 6o) state are presented in Figure 4a. Herein, it is assumed that, at r(Pt–C) = 5.0 Å, the structure is at its dissociation limit. At this limit, the doubly degenerate triplet states 13A1 and 23A1 are the lowest energy states, while the doubly degenerate singlet states 11A1 and 21A1 are the second lowest, and the third singlet state 31A1 is the highest. An analysis of the CASSCF wave function suggests that these triplet states are derived from the 3D state of Pt having the electron configuration (5d)9(6s)1 (Figure S1). Similarly, the 11A1 and 21A1 states are derived from the 1D state with the configuration (5d)9(6s)1, while the 31A1 state originates from the 1S state with the configuration (5d)10(6s)0. The normally degenerate states are split with regard to their energy levels due to the interactions of the Pt atom with the CO. Consequently, the energetic ordering of the 11A1 and 13A1 states is inverted at r(Pt–C) = 2.17 Å, and the ground state in the region over which r(Pt–C) < 2.17 Å is 11A1. Thus, the spin multiplicity of the ground state varies depending on the value of r(Pt–C). The potential energy curves obtained using the CASCI method based on ROHF orbitals are provided in Figure 4b. Although the energy level of the 13A1 state is relatively underestimated here as compared to the CASSCF results, the crossover of the 11A1 state with 13A1 was also predicted at this level of theory and appears at r(Pt–C) = 2.12 Å. These results imply that VQE calculations using fewer qubits could potentially describe the spin crossover in the ground state.

Figure 4.

Figure 4

Open in a new tab

Potential energy curves for the 11A1 (●), 21A1 (▲), 31A1 (■), 13A1 (○), and 23A1 (△) states as calculated using (a) the CASSCF method with the CAS(10e, 6o) space and (b) the CASCI method based on ROHF orbitals. The basis sets used in the CASSCF calculations were def2-QZVP for Pt and cc-pVQZ for C and O, while those in the CASCI calculations were def2-SVP for Pt and cc-pVDZ for C and O.

An analysis of the CASSCF wave functions with the CAS(10e, 6o) space suggested that the main configuration of the 13A1 state was (5d)9(6s)1 with a singly occupied 5dz2 orbital over the entire region, while that for the 21A1 and 23A1 states was (5d)9(6s)1 with a singly occupied dx2–y2 orbital. In contrast, the weights of the main configurations for the 11A1 and 31A1 states varied depending on r(Pt–C) (Figure S1). Here, the weights were calculated as squared coefficients of the configurations in the CASSCF wave functions. The main configurations for these states were (5d)9(6s)1 with a singly occupied 5dz2 orbital together with the closed-shell (5d)10(6s)0 configuration. For the 11A1 state, the configuration (5d)9(6s)1 was dominant at the dissociation limit, while (5d)10(6s)0 was dominant in the bonding region. Conversely, in the case of the 31A1 state, the configuration (5d)10(6s)0 was dominant at the dissociation limit, but (5d)9(6s)1 was the primary configuration throughout the bonding region. The total weights of these configurations were greater than 0.85 for all states over the entire region. Figure 5 shows the CASSCF natural orbitals and the associated occupation numbers at r(Pt–C) = 1.85 Å on behalf of the structures in the bonding region. The sum of the occupation numbers for the orbitals with a1 symmetry was nearly four, while the other orbitals were approximately doubly occupied. Similar results were obtained for the dissociation limit, as shown in Figure S2. Therefore, the singlet–triplet crossover was predicted reasonably well using the smaller active spaces CAS(4e, 3o) and CAS(2e, 2o) (Figure S3).

Figure 5.

Figure 5

Open in a new tab

Natural orbitals at r(Pt–C) = 1.85 Å for the singlet states calculated using the CASSCF method with the CAS(10e, 6o) space. These orbitals are derived from the (a) 5dxy, (b) 5dyz, (c) 5dxz, (d) 5dx2–y2, (e) 5dz2, and (f) 6s atomic orbitals of Pt. The associated symmetries are a2, b2, b1, a1, a1, and a1, respectively. The occupation numbers are shown below the orbitals.

The results of CASCI calculations based on the RHF orbitals were found to be inconsistent with those obtained using the CASSCF method (Figure S4). Specifically, the energetic ordering of the electronic states was 11A1 < 13A1 over the entire region, and a 11A1–13A1 crossover was not observed. Because the RHF orbitals were optimized for the closed-shell singlet state, the energy level of the electronic state having the primary configuration (5d)10(6s)0 could have been significantly underestimated. An analysis of the CASCI wave function revealed that one of the main configurations of 11A1 was derived from the (5d)10(6s)0 configuration of the Pt atom, while that of the 13A1 state originated from a (5d)9(6s)1 configuration. Thus, the energy level of the 11A1 state was relatively underestimated, resulting in the absence of the 11A1–13A1 crossover. In contrast, in the case of the CASCI calculations based on ROHF orbitals, the energy level of the 13A1 state was underestimated relative to those of the 11A1 state because the orbitals were optimized for the lowest triplet state. Consequently, the 11A1–13A1 crossover was observed. The effect of the basis set was found to be minimal, and the 11A1–13A1 crossover could be reproduced even with smaller basis sets (Figure S5). Therefore, the combination of def2-SVP for Pt and cc-pVDZ for C and O, which were the smallest basis sets among those examined, was adopted for the VQE calculations to reduce the computational load.

VQE Calculations

The potential energy curves calculated using the VQE technique with the statevector simulator are plotted in Figure 6a along with the CASCI results. These VQE calculations with the simulator reproduced the singlet potential energy curve obtained from the CASCI process over the range of r(Pt–C) < 2.12 Å and the triplet potential energy curve over the range of r(Pt–C) > 2.12 Å. Thus, the VQE values follow the ground-state potential energy curve over the entire region. These results suggest that the VQE algorithm is able to closely predict a reaction pathway along a ground-state potential energy curve including a spin crossover. The potential energies at r(Pt–C) = 1.846 and 3.0 Å were also calculated using the IBM quantum device, and the resulting energies and the associated errors obtained from three replicate VQE calculations are collected in Table 1. The computational time is shown in Table S6. These results qualitatively reproduce the CASCI data as plotted in Figure 6a. The calculated values were close to the singlet potential energy curve generated via the CASCI method for r(Pt–C) = 1.846 Å and the triplet potential energy curve obtained from the CASCI technique for r(Pt–C) = 3.0 Å. The differences between the potential energy values acquired from the IBM quantum device and the exact values calculated using the CASCI method are plotted in Figure 6b. It is evident from this plot that these differences were all less than ±0.003 hartree (±2 kcal/mol). The discrepancies between the actual resulting energies are larger than the standard errors of energies, suggesting the existence of a time-dependent bias that induces the displacement of measured energies during our three VQE calculations. Time-varying device noise induced during the qubit operation processes may be responsible for this bias. The discrepancy between the results obtained with the simulator and the actual quantum device can also be attributed to quantum device noise, which induces a bias that alters the measured values from the results obtained by the simulator. To mitigate the effect of noise, it is necessary to implement error mitigation techniques that not only address readout errors but also errors arising from gate operations and other sources.

Figure 6.

Figure 6

Open in a new tab

(a) Potential energy curves of the singlet ground state (solid line) and the triplet ground state (dotted line) calculated using the CASCI method, the potential energies obtained using the VQE approach with a statevector simulator (△), and the IBM ibm_canberra quantum device (●). (b) The energy difference from the CASCI potential energies obtained from the simulator (△) and the IBM ibm_canberra quantum device (●). The range indicated by the two dashed lines equals ±0.0016 hartree, equivalent to so-called chemical accuracy (±1 kcal/mol).

Table 1. Potential Energies and Total Spin Angular Momentum Values Calculated Using the IBM ibm_canberra Quantum Device, Employing Three Replicate VQE Calculationsa.

r(Pt–C) ECASCI ⟨Ĥ⟩ e⟨Ĥ⟩ ⟨Ŝ2⟩CASCI ⟨Ŝ2⟩ e⟨Ŝ2⟩
1.846 –231.1477 –231.1451 0.0009 0.0 –0.06 0.19
    –231.1460 0.0008   0.01 0.19
    –231.1460 0.0008   0.36 0.19
3.0 –231.1364 –231.1342 0.0005 2.0 1.81 0.13
    –231.1372 0.0005   2.01 0.09
    –231.1355 0.0005   1.86 0.14
Open in a new tab
a

r(Pt–C) denotes the bond length between Pt and C in angstroms, while ECASCI, ⟨Ĥ⟩, and e⟨Ĥ⟩ denote the reference potential energy calculated using the CASCI method, the expected value of the Hamiltonian, and the associated standard error, respectively, in hartree. ⟨Ŝ2⟩CASCI, ⟨Ŝ⟩2, and e⟨Ŝ⟩2 denote the reference CASCI value for the total spin angular momentum, the expected value for Ŝ2, and the associated standard error, respectively. The three values at each r(Pt–C) correspond to the results of three replicate VQE calculations.

The calculated values for the spin squared operator, ⟨Ŝ2⟩, are also summarized in Table 1 and plotted in Figure 7. All of the calculated ⟨Ŝ2⟩ values were within ±0.5 of the reference values calculated using the CASCI technique. Consequently, the singlet and triplet states could be clearly distinguished when these values were rounded off to the nearest integers. The occurrence of a negative expectation value for Ŝ2 can be induced by both statistical error and device noise in the measurement of Pauli operators. To avoid such artifacts, it is necessary to increase the number of shots in the measurement to reduce statistical error and improve the error mitigation level to suppress device noise. The errors in these results are sufficiently small such that the change in spin multiplicity can be recognized even though only 16 shots were carried out for each Pauli term in Ŝ2. It is known that the minimal difference in the ⟨Ŝ2⟩ values between the electronic states having different spin multiplicities will be 2.0 for a system with an even number of electrons; for example, the ⟨Ŝ2⟩ values are 0.0 and 2.0 for singlet and triplet states, respectively. This value will be 3.0 for a system with an odd number of electrons; for example, the ⟨Ŝ2⟩ values are 0.75 and 3.75 for doublet and quartet states, respectively. Accordingly, the change in spin multiplicity can be detected even in the case of results that have a moderate level of accuracy when the parity of the electron number is conserved. Because the standard error associated with the expected value of the Pauli term P̂ is 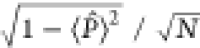Inline graphic, where N is the shot number, approximately 10 shots are sufficient to obtain the required precision in the ones place for a single Pauli term in the absence of noise. The spin squared operator used in these calculations, Ŝ2, is expressed as

graphic file with name ao3c01875_m005.jpg 4

where X̂i, Ŷi, and Ẑi denote the Pauli operators for qubit i (i = 0, 1) along the x, y, and z directions, respectively. Here, we can let eP equal the largest standard error among the standard errors of ⟨X̂0X̂1⟩, ⟨Ŷ0Ŷ1⟩, and ⟨Ẑ0Ẑ1⟩ using N shots. On the basis of the propagation of error, the standard error of ⟨Ŝ2⟩ is then

graphic file with name ao3c01875_m006.jpg 5

Therefore, the use of 10 shots for a single Pauli term is sufficient to obtain the necessary numeric precision in the ones place for ⟨Ŝ2⟩ in these calculations. On this basis, the spin multiplicity of the ground state could be successfully calculated via the VQE process even with present-day noisy devices because the determination of the square of the total spin angular momentum is essentially unaffected by noise.

Figure 7.

Figure 7

Open in a new tab

Expected values of the spin squared operator ⟨Ŝ2⟩ as obtained from the simulator (△) and the IBM ibm_canberra quantum device (●). The solid and dotted lines show the expected values of the spin squared operator ⟨Ŝ2⟩, which are 0.0 and 2.0 for the singlet and triplet states, respectively.

The total spin angular momentum Ŝ can be determined with a smaller number of measurements than are required for Ĥ. This can be explained on the basis of the number of Pauli terms that appear in the Ŝ2 operator. The spin angular momentum along the k (k = x,y,z) direction can be expressed as70

graphic file with name ao3c01875_m007.jpg 6

where n is the number of qubits, σs,s′k denotes the (s, s′) element of the Pauli matrix in the k direction, and ci,s† and ci,s are the Fermionic creation and annihilation operators. The total spin squared operator Ŝ2 can be expressed as the summation of the squared spin angular momentum along the x, y, z directions, written as

graphic file with name ao3c01875_m008.jpg 7

Note that this is the product of two summations, where the index runs over all n qubits. Using a naive strategy, the number of Pauli terms in the observable Ŝ2 is O(n2), which is smaller than the number of Pauli terms O(n4) in the Hamiltonian Ĥ.

Finally, it is helpful to discuss the present limitations of the VQE algorithm as a means of determining the total spin angular momentum of the ground state. To identify the ground state among the various spin states, the ansatz should suitably represent both the ground state and other electronic states having different spin multiplicities. In addition, the number of parameters to be optimized should be sufficiently small. Unfortunately, it is still unclear whether such an ansatz exists. In this context, developing a sophisticated method for the state preparation of the quantum device will be an important challenge in future. Assuming that this is possible, the present work indicates that the total spin angular momentum could be measured with a small number of shots.

Conclusion

Working within the framework of the VQE quantum-classical hybrid algorithm, the ground state of a molecular system was calculated while minimizing the cost function. The energy and spin multiplicity of the ground state could be simultaneously explored when applying this algorithm without penalty terms on the spin angular momentum. This computational scheme could be useful in the calculation of a strongly correlated system for which the spin multiplicity of the ground state cannot be easily estimated. In this study, the adsorption of CO onto a single Pt atom was investigated as a model system. VQE calculations using the statevector simulator successfully traced the ground state over the entire potential energy curve. These calculations converged to the singlet state in the bonding region but the triplet state at the dissociation limit. In addition, the potential energies acquired using an actual quantum device qualitatively reproduced the CASCI energy values for both the bonding and the dissociation regions. Furthermore, the spin multiplicities in the bonding and dissociation regions could be clearly distinguished despite the noise effect. Thus, using the VQE algorithm, it was possible to identify a change in spin multiplicity moving along the ground-state potential energy curve without specifying the spin multiplicity in advance. The results of this research suggest that discrete values of parameters such as spin angular momentum can be determined with reasonable accuracy even using NISQ devices if the ansatz that is adopted has sufficient expressibility to describe the multispin states, including the target state.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c01875.

  • Calculated electronic state total energies (Tables S1–S5); weights of electron configurations in the CASSCF wave function with the CAS(10e, 6o) state (Figure S1); natural orbitals at r(Pt–C) = 5.00 Å (Figure S2); potential energy curves calculated using the CASSCF method with the CAS(4e, 3o) and CAS(2e, 2o) states (Figure S3); CASCI results based on RHF orbitals (Figure S4); and potential energy curves calculated using the CASCI method with triple-ζ and quadruple-ζ basis sets (Figure S5) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao3c01875_si_001.pdf (600.6KB, pdf)

References

  1. Höök M.; Tang X. Depletion of fossil fuels and anthropogenic climate change-A review. Energy Policy 2013, 52, 797–809. 10.1016/j.enpol.2012.10.046. [DOI] [Google Scholar]
  2. Welsby D.; Price J.; Pye S.; Ekins P. Unextractable fossil fuels in a 1.5 C world. Nature 2021, 597, 230–234. 10.1038/s41586-021-03821-8. [DOI] [PubMed] [Google Scholar]
  3. Yagi M.; Kaneko M. Molecular catalysts for water oxidation. Chem. Rev. 2001, 101, 21–36. 10.1021/cr980108l. [DOI] [PubMed] [Google Scholar]
  4. Kärkäs M. D.; Verho O.; Johnston E. V.; Åkermark B. Artificial photosynthesis: molecular systems for catalytic water oxidation. Chem. Rev. 2014, 114, 11863–12001. 10.1021/cr400572f. [DOI] [PubMed] [Google Scholar]
  5. Blakemore J. D.; Crabtree R. H.; Brudvig G. W. Molecular catalysts for water oxidation. Chem. Rev. 2015, 115, 12974–13005. 10.1021/acs.chemrev.5b00122. [DOI] [PubMed] [Google Scholar]
  6. Lloyd L.Handbook of Industrial Catalysts; Springer Science & Business Media: New York, 2011. [Google Scholar]
  7. Hagen J.Industrial Catalysis: A Practical Approach; John Wiley & Sons: New York, 2015. [Google Scholar]
  8. Sherrill C. D.; Schaefer H. F. III. Advances in Quantum Chemistry; Elsevier: New York, 1999; Vol. 34, pp 143–269. [Google Scholar]
  9. Olsen J.; Jørgensen P.; Koch H.; Balkova A.; Bartlett R. J. Full configuration-interaction and state of the art correlation calculations on water in a valence double-zeta basis with polarization functions. J. Chem. Phys. 1996, 104, 8007–8015. 10.1063/1.471518. [DOI] [Google Scholar]
  10. Cao Y.; Romero J.; Olson J. P.; Degroote M.; Johnson P. D.; Kieferová M.; Kivlichan I. D.; Menke T.; Peropadre B.; Sawaya N. P.; et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 2019, 119, 10856–10915. 10.1021/acs.chemrev.8b00803. [DOI] [PubMed] [Google Scholar]
  11. McArdle S.; Endo S.; Aspuru-Guzik A.; Benjamin S. C.; Yuan X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. 10.1103/RevModPhys.92.015003. [DOI] [Google Scholar]
  12. Abrams D. S.; Lloyd S. Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors. Phys. Rev. Lett. 1999, 83, 5162–5165. 10.1103/PhysRevLett.83.5162. [DOI] [Google Scholar]
  13. Aspuru-Guzik A.; Dutoi A. D.; Love P. J.; Head-Gordon M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. 10.1126/science.1113479. [DOI] [PubMed] [Google Scholar]
  14. Wecker D.; Bauer B.; Clark B. K.; Hastings M. B.; Troyer M. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys. Rev. A 2014, 90, 022305. 10.1103/PhysRevA.90.022305. [DOI] [Google Scholar]
  15. Babbush R.; Berry D. W.; Sanders Y. R.; Kivlichan I. D.; Scherer A.; Wei A. Y.; Love P. J.; Aspuru-Guzik A. Exponentially more precise quantum simulation of fermions in the configuration interaction representation. Quantum Sci. Technol. 2018, 3, 015006. 10.1088/2058-9565/aa9463. [DOI] [Google Scholar]
  16. Kitagawa Y.; Chen Y.; Nakatani N.; Nakayama A.; Hasegawa J. A DFT and multi-configurational perturbation theory study on O2 binding to a model heme compound via the spin-change barrier. Phys. Chem. Chem. Phys. 2016, 18, 18137–18144. 10.1039/C6CP02329K. [DOI] [PubMed] [Google Scholar]
  17. Watanabe K.; Nakatani N.; Nakayama A.; Higashi M.; Hasegawa J. Spin-blocking effect in CO and H2 binding reactions to molybdenocene and tungstenocene: A theoretical study on the reaction mechanism via the minimum energy intersystem crossing point. Inorg. Chem. 2016, 55, 8082–8090. 10.1021/acs.inorgchem.6b01187. [DOI] [PubMed] [Google Scholar]
  18. Jiang Y.-Y.; Jiang J.-L.; Fu Y. Mechanism of vanadium-catalyzed deoxydehydration of vicinal diols: Spin-crossover-involved processes. Organometallics 2016, 35, 3388–3396. 10.1021/acs.organomet.6b00602. [DOI] [Google Scholar]
  19. Kwon D.-H.; Proctor M.; Mendoza S.; Uyeda C.; Ess D. H. Catalytic dinuclear nickel spin crossover mechanism and selectivity for alkyne cyclotrimerization. ACS Catal. 2017, 7, 4796–4804. 10.1021/acscatal.7b00978. [DOI] [Google Scholar]
  20. Nakatani N.; Nakayama A.; Hasegawa J.; Nakatsuji H.; Kirtman B.; Ozaki Y.. Frontiers of Quantum Chemistry; Springer Singapore: Singapore, 2018; pp 289–313. [Google Scholar]
  21. Li X.; et al. Identification of the electronic and structural dynamics of catalytic centers in single-Fe-atom material. Chem. 2020, 6, 3440–3454. 10.1016/j.chempr.2020.10.027. [DOI] [Google Scholar]
  22. Radon M.; Pierloot K. Binding of CO, NO, and O2 to heme by density functional and multireference ab initio calculations. J. Phys. Chem. A 2008, 112, 11824–11832. 10.1021/jp806075b. [DOI] [PubMed] [Google Scholar]
  23. Sebetci A. Does spin-orbit coupling effect favor planar structures for small platinum clusters?. Phys. Chem. Chem. Phys. 2009, 11, 921–925. 10.1039/B810837D. [DOI] [PubMed] [Google Scholar]
  24. Ali M. E.; Sanyal B.; Oppeneer P. M. Electronic structure, spin-states, and spin-crossover reaction of heme-related Fe-porphyrins: a theoretical perspective. J. Phys. Chem. B 2012, 116, 5849–5859. 10.1021/jp3021563. [DOI] [PubMed] [Google Scholar]
  25. García-Cruz R.; Poulain E.; Hernández-Pérez I.; Reyes-Nava J. A.; González-Torres J. C.; Rubio-Ponce A.; Olvera-Neria O. Effect of Spin Multiplicity in O2 Adsorption and Dissociation on Small Bimetallic AuAg Clusters. J. Phys. Chem. A 2017, 121, 6079–6089. 10.1021/acs.jpca.7b01968. [DOI] [PubMed] [Google Scholar]
  26. Zhang F.; Zhang H.; Xin W.; Chen P.; Hu Y.; Zhang X.; Zhao Y. Probing the structural evolution and electronic properties of divalent metal Be2Mg n clusters from small to medium-size. Sci. Rep. 2020, 10, 6052. 10.1038/s41598-020-63237-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Preskill J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. 10.22331/q-2018-08-06-79. [DOI] [Google Scholar]
  28. Wang D.; Higgott O.; Brierley S. Accelerated variational quantum eigensolver. Phys. Rev. Lett. 2019, 122, 140504. 10.1103/PhysRevLett.122.140504. [DOI] [PubMed] [Google Scholar]
  29. Sugisaki K.; Sakai C.; Toyota K.; Sato K.; Shiomi D.; Takui T. Bayesian phase difference estimation: a general quantum algorithm for the direct calculation of energy gaps. Phys. Chem. Chem. Phys. 2021, 23, 20152–20162. 10.1039/D1CP03156B. [DOI] [PubMed] [Google Scholar]
  30. Peruzzo A.; McClean J.; Shadbolt P.; Yung M.-H.; Zhou X.-Q.; Love P. J.; Aspuru-Guzik A.; O’brien J. L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 1–7. 10.1038/ncomms5213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. McClean J. R.; Romero J.; Babbush R.; Aspuru-Guzik A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 2016, 18, 023023. 10.1088/1367-2630/18/2/023023. [DOI] [Google Scholar]
  32. Roszak S.; Balasubramanian K. Potential energy curves for platinum-carbon monoxide interactions. J. Phys. Chem. 1993, 97, 11238–11241. 10.1021/j100145a020. [DOI] [Google Scholar]
  33. Wu Z.; Li H.; Zhang H.; Meng J. Electronic structures of MCO (M= Nb, Ta, Rh, Ir, Pd, Pt) molecules by density functional theory. J. Phys. Chem. A 2004, 108, 10906–10910. 10.1021/jp046821y. [DOI] [Google Scholar]
  34. Blaise J.; Verges J.; Wyart J.; Engleman R. J. Energy-levels of neutral platinum. J. Res. Natl. Inst 1992, 97, 213–216. 10.6028/jres.097.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tan H.; Liao M.; Balasubramanian K. Potential energy surfaces of RuCO. Chemical physics letters 1998, 284, 1–5. 10.1016/S0009-2614(97)01370-5. [DOI] [Google Scholar]
  36. Dai D.; Balasubramanian K. Potential energy surfaces for Rh–CO, Rh–OC, Ir–CO, and Ir–OC interactions. J. Chem. Phys. 1994, 101, 2148–2156. 10.1063/1.468474. [DOI] [Google Scholar]
  37. Tan H.; Liao M.; Balasubramanian K. Potential energy surfaces of OsCO. Chemical physics letters 1998, 290, 458–464. 10.1016/S0009-2614(98)00536-3. [DOI] [Google Scholar]
  38. Matsen F. Spin-free quantum chemistry. Adv. Quantum Chem. 1964, 1, 59–114. 10.1016/S0065-3276(08)60375-5. [DOI] [Google Scholar]
  39. Matsen F.; Nelin C. Spin-Free quantum chemistry. XXII. Multiconfiguration self-consistent field theory. Int. J. Quantum Chem. 1981, 20, 861–878. 10.1002/qua.560200409. [DOI] [Google Scholar]
  40. Balasubramanian K. The combinatorics of graphical unitary group approach to many electron correlation. Theor. Chim. Acta 1981, 59, 237–250. 10.1007/BF00551353. [DOI] [Google Scholar]
  41. David Sherrill C.; Schaefer H. F.. The Configuration Interaction Method: Advances in Highly Correlated. In Advances in Quantum Chemistry; Löwdin P.-O., Sabin J. R., Zerner M. C., Brändas E., Eds.; Academic Press: New York, 1999; Vol. 34, pp 143–269. [Google Scholar]
  42. Olsen J.; Roos B. O.; Jørgensen P.; Jensen H. J. A. Determinant based configuration interaction algorithms for complete and restricted configuration interaction spaces. J. Chem. Phys. 1988, 89, 2185–2192. 10.1063/1.455063. [DOI] [Google Scholar]
  43. Olsen J.; Jørgensen P.; Simons J. Passing the one-billion limit in full configuration-interaction (FCI) calculations. Chem. Phys. Lett. 1990, 169, 463–472. 10.1016/0009-2614(90)85633-N. [DOI] [Google Scholar]
  44. Cramer C. J.Essentials of Computational Chemistry: Theories and Models, 2nd ed.; John Wiley & Sons: New York, 2004. [Google Scholar]
  45. Ryabinkin I. G.; Genin S. N.; Izmaylov A. F. Constrained variational quantum eigensolver: Quantum computer search engine in the Fock space. J. Chem. Theory Comput. 2019, 15, 249–255. 10.1021/acs.jctc.8b00943. [DOI] [PubMed] [Google Scholar]
  46. Kuroiwa K.; Nakagawa Y. O. Penalty methods for a variational quantum eigensolver. Phys. Rev. Res. 2021, 3, 013197. 10.1103/PhysRevResearch.3.013197. [DOI] [Google Scholar]
  47. Balasubramanian K. Relativity and chemical bonding. J. Phys. Chem. 1989, 93, 6585–6596. 10.1021/j100355a005. [DOI] [Google Scholar]
  48. Vosko S. H.; Wilk L.; Nusair M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
  49. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  50. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  51. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  52. Weigend F.; Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
  53. Dunning T. H. Jr Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
  54. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; et al. Gaussian 16, revision C.01; Gaussian, Inc.: Wallingford, CT, 2016.
  55. Bunker P.; Jensen P.. Molecular Symmetry and Spectroscopy. NRC Monograph Publishing Program; NRC Research Press: Canada, 2006. [Google Scholar]
  56. Knecht S.; Jensen H. J. A.; Fleig T. Large-scale parallel configuration interaction. II. Two-and four-component double-group general active space implementation with application to BiH. J. Chem. Phys. 2010, 132, 014108. 10.1063/1.3276157. [DOI] [PubMed] [Google Scholar]
  57. Roos B. O.; Taylor P. R.; Sigbahn P. E. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. 10.1016/0301-0104(80)80045-0. [DOI] [Google Scholar]
  58. Roos B. O. The complete active space self-consistent field method and its applications in electronic structure calculations. Adv. Chem. Phys. 1987, 69, 399–445. [Google Scholar]
  59. Levine B. G.; Durden A. S.; Esch M. P.; Liang F.; Shu Y. CAS without SCF-Why to use CASCI and where to get the orbitals. J. Chem. Phys. 2021, 154, 090902. 10.1063/5.0042147. [DOI] [PubMed] [Google Scholar]
  60. Mizukami W.; Mitarai K.; Nakagawa Y. O.; Yamamoto T.; Yan T.; Ohnishi Y.-y Orbital optimized unitary coupled cluster theory for quantum computer. Phys. Rev. Res. 2020, 2, 033421. 10.1103/PhysRevResearch.2.033421. [DOI] [Google Scholar]
  61. Omiya K.; Nakagawa Y. O.; Koh S.; Mizukami W.; Gao Q.; Kobayashi T. Analytical energy gradient for state-averaged orbital-optimized variational quantum eigensolvers and its application to a photochemical reaction. J. Chem. Theory Comput. 2022, 18, 741–748. 10.1021/acs.jctc.1c00877. [DOI] [PubMed] [Google Scholar]
  62. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
  63. Gordon M. S.; Schmidt M. W.. Theory and Applications of Computational Chemistry; Elsevier: New York, 2005; pp 1167–1189. [Google Scholar]
  64. Abraham H.; et al. Qiskit: An Open-Source Framework for Quantum Computing, 2021. [Google Scholar]
  65. IBM Quantum; https://cloud.ibm.com/quantum/resources/systems, 2021.
  66. Sun Q.; Berkelbach T. C.; Blunt N. S.; Booth G. H.; Guo S.; Li Z.; Liu J.; McClain J. D.; Sayfutyarova E. R.; Sharma S.; Wouters S.; Chan G. K.-L. PySCF: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1340. 10.1002/wcms.1340. [DOI] [Google Scholar]
  67. Kandala A.; Mezzacapo A.; Temme K.; Takita M.; Brink M.; Chow J. M.; Gambetta J. M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. 10.1038/nature23879. [DOI] [PubMed] [Google Scholar]
  68. Nakanishi K. M.; Fujii K.; Todo S. Sequential minimal optimization for quantum-classical hybrid algorithms. Phys. Rev. Res. 2020, 2, 043158. 10.1103/PhysRevResearch.2.043158. [DOI] [Google Scholar]
  69. van den Berg E.; Minev Z. K.; Temme K. Model-free readout-error mitigation for quantum expectation values. Phys. Rev. A 2022, 105, 032620. 10.1103/PhysRevA.105.032620. [DOI] [Google Scholar]
  70. Auerbach A.Interacting Electrons and Quantum Magnetism; Springer Science & Business Media: New York, 1994. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c01875_si_001.pdf (600.6KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES