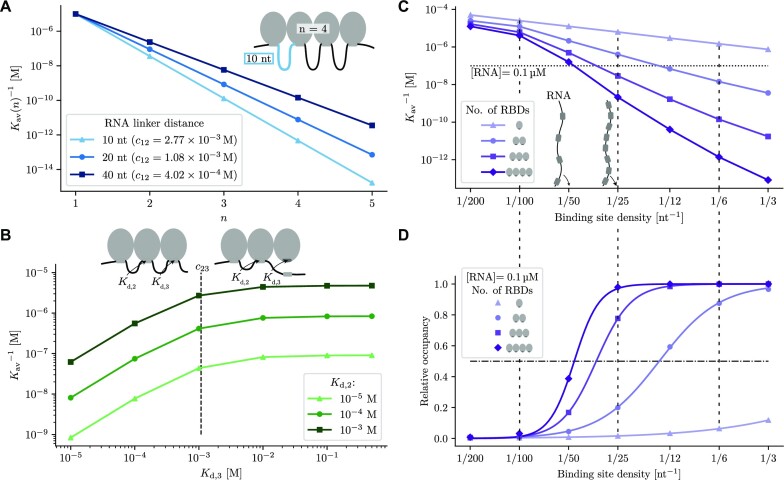
Figure 5.

Dependence of the avidity (effective association constant) of RBPs on the number of RBDs, their K_d’s, the effective local concentrations c_ij, and the binding site density on the RNA. (A) The inverse avidity 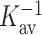decreases exponentially with the number of binding domains n, because each added binding site multiplies the avidity by ∼K_{a, i} times the local concentration c_{i − 1, i} of the free i’th RNA binding site at the site of the i’th free RBD (equation 4). The slope thus depends on the spacing of binding sites via c_{i − 1, i}. All RBD K_d’s were set to 10 μM and distances d between rigidly linked binding domains to 2 nm. (B) Individual RBDs contribute proportionally to the total avidity as long as their K_{d, i} is less than the local concentration, 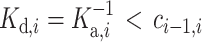(here shown for i = 3). The K_d for the first domain is K_{d, 1} = 10 μM, the K_ds for the second and third domain are varied as indicated. 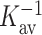was calculated for equal distances between rigidly linked binding domains of 2 nm and an RNA linker length of 20 nt. (C) The inverse avidity decreases with the binding site density on the RNA. For this plot, we approximately neglect non-sequential binding modes, which are much less populated than the sequential ones. K_ds of individual domains were 50 μM and the total RNA length was 200 nt. The horizontal line indicates a concentration of 0.1 μM used for the calculations in (D). (D) Binding probability of RBPs as measured by 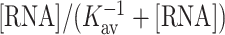as a function of binding site density on the RNA at an RNA concentration of 0.1 μM (horizontal line in (C)). Curves show fits with sigmoidal Hill-functions, with Hill coefficients of h₁ = 0.99, h₂ = 2.35, h₃ = 4.01 and h₄ = 5.7 for one to four domains, respectively. Note the strongly cooperative, switch-like behaviour for n = 4 RBDs.