Abstract
Nanofiltration can be used as the last step in the purification of the biomolecules that are present in many industrial by-products, such as biological protein hydrolysates. The present study explored the variation in glycine and triglycine rejections in binary solutions with NaCl at different feed pHs with two nanofiltration membranes: MPF-36 and Desal 5DK with molecular weight cut-offs of 1000 and 200 g mol−1, respectively. First, water permeability coefficient showed a n-shaped curve with feed pH, which was more evident for the MPF-36 membrane. Second, membrane performance with single solutions was studied and the experimental data were fitted with the Donnan steric pore model with dielectric exclusion (DSPM-DE) to explain the variations of solute rejection with feed pHs. Glucose rejection was assessed to estimate the membrane pore radius of the MPF-36 membrane, and a pH dependence was observed. For a tight membrane (Desal 5DK), glucose rejection was close to unity and the membrane pore radius was estimated from the glycine rejection in the feed pH range from 3.7 to 8.4. Glycine and triglycine rejections showed a pH-dependence with a u-shaped curve, even for the zwitterion species. In binary solutions, glycine and triglycine rejections decreased with NaCl concentration, especially in the MPF-36 membrane. Triglycine rejection was always higher than NaCl rejection and it was estimated that triglycine can be desalted using a continuous diananofiltration the Desal 5DK membrane.
Keywords: Nanofiltration membranes, Modelling, Dielectric exclusion, Amino acid purification, Diananofiltration
1. Introduction
Different sectors in the biotechnological and food industry produce great amounts of biological by-products that contain bioactive molecules such as proteins and peptides, which can be re-used to reduce their environmental impact and promote their valorisation [1,2]. Membrane separation technology has been used to fractionate and concentrate protein hydrolysates from by-products with biological and functional properties [3]. First, the fractioning process of proteins and peptides involves the use of ultrafiltration membranes in several steps, with membranes that present different molecular weight cut-off (MWCO) values [4,5]. Depending on the purity required, the last nanofiltration step enables the concentration of peptides and amino acids of low molecular weight by avoiding an excessive concentration of salts [6]. This last step can be achieved through concentration mode or diafiltration using NF membranes (a process also called diananofiltration), both can operate in continuous and discontinuous mode [7]. The concentration mode leads to the removal of the smallest molecules in the permeate while the biggest ones are rejected and concentrated in the rejection stream, increasing the feed concentration during the process and the concentration polarization and fouling on the membrane surface [8,9]. Nevertheless, diananofiltration consists in the continuous addition of fresh water to the feed solution at the same rate as the permeate is collected, separating the molecules without increasing in their concentrations [10].
Nanofiltration (NF) membranes comprise three stacked porous layers of different polymers. The mean pore size of the top layer (also called the active layer) is generally 2 nm; thus, this layer can retain molecules of less than 1000 Da [11,12]. The active layer is an imperfect crosslinking polymer with ionisable groups, which confer a specific charge on the membrane depending on the solution subjected to nanofiltration. Generally, NF membranes are amphoteric, being positively, negatively, or net-zero charged depending on the pH of the feed solution [13,14]. Due to this variation, the membrane has an isoelectric point (IEP) that is characteristic of each membrane. Apart from the pH, membrane charge also depends on the composition of the feed solution due to the adsorption of cations and counterions on the membrane surface [15,16]. Therefore, the retention of molecules by NF membranes is due to steric and electric exclusion via attraction or repulsion between the solute molecule and membrane charge, as well as to dielectric exclusion via variations in the dielectric constant inside the pore [17].
The influence of the feed pH on solute rejection has been relatively well studied. Generally, the rejection of inorganic salts by membranes varies significantly with the feed pH due to changes in the interaction between the solute and membrane surface [18]. For instance, the rejection of a simple salt such as NaCl is reduced with increasing feed pH. Although the rejection of salts containing multi-valent ions also shows a pH-dependence, the trend differs from that of NaCl rejection [19,20]. The rejection of salts as a function of the pH follows different patterns, being nearly constant, increasing, or reaching a minimum in different cases [21]. This variation in solute rejection with pH is attributed to the influence of the feed pH on the membrane surface charge due to the dissociation of functional groups, leading to a negative surface membrane charge at an alkaline pH and a positive surface membrane charge at an acidic pH [22,23].
The retention of solutes (inorganic salts and also organic charged molecules) by membranes has been explained mathematically by the Donnan steric pore model with dielectric exclusion (DSPM-DE), which considers the partitioning equilibrium between the external solution and membrane surface, as well as solute transport through charged membrane pores [24]. Donnan exclusion is due to the repulsion between the charged solutes and the charged membrane surface. Dielectric exclusion originates from the difference between the dielectric constant of the external bulk solution and that inside the membrane pores [25]. Dielectric exclusion arises from image forces and ion solvation [26]. On the one hand, the first mechanism of image forces considers the electrostatic interactions between the ions with fixed charges inside the pore and free ions, which are expected to be stronger than the interactions in the bulk solution [27]. However, there is no evidence to confirm that the dielectric exclusion due to image forces inside the nanopores plays a significant role in the partitioning equilibrium [28]. On the other hand, the ion solvation mechanism is based on the presence of a single layer of oriented water molecules on the membrane pore wall that significantly reduces the dielectric constant of the pore and increases dielectric exclusion [17]. In the literature, ion solvation is the mechanism that is most widely accepted as an explanation of dielectric exclusion.
Once the ion or molecule has arrived at the membrane pore, ion transport through the membrane pores is generally described by applying the extended Nernst–Planck equation, where it is assumed that the radial concentration gradient can be ignored because the pores are cylindrical and sufficiently narrow [29]. Ion flux through the membrane depends on the convention flux, ion diffusivity and the potential gradient inside the pores [30]. The key parameters of the DSPM-DE predicting the outcomes of the NF process are the effective average pore radius (rp), the effective thickness−porosity ratio (Δx/Ak), the effective membrane charge density (Xd) and the dielectric pore constant (εp). These parameters can be estimated from the experimental rejection of different solutes in order to determine the membrane performance [[31], [32], [33]].
The aim of the present study was to evaluate the effect of pH and NaCl on the rejection of low molecular weight organic molecules with two NF membranes. The solute rejections were fitted by the DSPM-DE to explain the conformational changes in the NF membranes with the feed pH and NaCl. First, the water permeability and the rejection of glucose were analysed to evaluate the performance of the two membranes at different feed pHs. Furthermore, the rejection of glycine and triglycine in single solute solutions and binary solutions with NaCl was explored to find the correlation of the key parameters of the DSPM-DE with feed pH. The results should improve our understanding the desalting process with the NF membranes that are used in the last step in the fractioning and concentration of peptides from industrial by-products.
2. Materials and methods
2.1. Feed solutions and membranes
Single solute and binary solutions were prepared at different pH values. All the chemicals used (glucose, glycine, triglycine and NaCl) were supplied by Sigma-Aldrich (Spain) and were obtained in the pure grade. The properties are shown in Table 1. Pure water came from the Milli-Q water purification system and was filtered through a membrane with a pore diameter of 45 μm. Solute concentrations were fixed at 10 mM for organic solutes and 100 mM for NaCl. The pH was adjusted by the dropwise addition of HCl or NaOH solution.
Table 1.
- Physical properties of the solutes used in this study.
| Species | MW (g mol−1) | pka1 | pka2 | rs (nm) | Ds (109 m2 s−1) |
|---|---|---|---|---|---|
| Glucose | 180.2 | – | – | 0.365 | 0.586 |
| Glycine | 75.0 | 2.37 | 9.60 | 0.245 | 0.873 |
| Triglycine | 189.2 | 3.23 | 8.09 | 0.375a | 0.571 |
| Na+ | 23.0 | – | – | 0.184b | 1.163 |
| Cl− | 35.4 | – | – | 0.121b | 1.768 |
rs calculated using the chemistry software ChemSketch (ACD/Labs) by means of atomic additive increments.
rs corresponding to the Stoke's radius.
The polymeric flat membranes used in this study were SelRO® MPF-36 (Koch; Wilmington, MA, USA), with a nominal molecular weight cut-off (MWCO) of 1000 g mol−1, and Desal 5DK (GEOsmonics; France), with a nominal MWCO of 200 g mol−1. The MPF-36 membrane is a proprietary thin-film composite membrane, with a maximum operating temperature of 70 °C and a functional pH range of 1–13. The Desal 5DK membrane is a thin-film composite membrane with a polyamide top layer. It can operate up to 90 °C, but the optimal pH range is 2–11. These variations in the characteristics of the two membranes can lead to different nanofiltration performances. According to previous studies, the membrane IEP is observed at a pH of 6.5 and 4.5 for the MPF-36 and Desal 5DK membrane, respectively [34,35], when they were measured as the minimum NaCl rejection with pH. For their part, zeta-potential measurements lead to a lower membrane IEP: 3.8 for Desal 5DK [36] and 7.2 for MPF-36 [12].
2.2. Experimental set-up
The experimental device consisted of a reservoir tank, a pump, a closed-pipe pressure dampener to prevent pressure oscillations, pressure gauges, a filtration cell, and flow meters for the retentate and permeate. Nanofiltration of the solutions was carried out in a laboratory-scale SEPA CF II membrane cell (Osmonics, Minnetonka, MN, USA). Nanofiltration of the solutions was carried out in a laboratory-scale SEPA CF II membrane cell. The feed channel had a length of 14.7 cm and a rectangular cross section 9.5 cm wide. The feed chamber contains a feed spacer, consisting of a diamond-shaped plastic mesh that was 0.43 mm (17 mil) thick and acted as a turbulence promoter. The flat membrane was in the upper side of the channel with a total membrane filtration area of 140 cm2. All the experiments were conducted at a crossflow velocity of 1 m/s, which is enough to minimise the concentration polarization when it is operated with low solute concentration solutions [37].
First, the membranes were conditioned with demineralised water at room temperature for 24 h. Then, the membranes were placed into the cell and pressurised with pure water at a constant temperature for 2 h. All experiments were conducted in the steady-state mode, in which the permeate stream was recycled to the feed vessel at a fixed temperature of 20 ± 0.5 °C, with the feed tank immersed in a thermostatic bath.
Nanofiltration performance was determined at a constant transmembrane pressure. After 60 min, the solute concentration, conductivity, the pH of the retentate and permeate streams, and the permeate flux rate were measured. It has been previously confirmed that steady state is reached at this time (after 60 min). The transmembrane pressure ranged from 5 to 25 bars and the procedure was repeated at each pressure. The organic solute concentration was determined as the total organic carbon (TOC) using an ASI-V Shimadzu analyser. The NaCl concentration and pH of the solutions were determined from conductivity measurements using IntelliCAL™ CDC and PHC probes connected to an HQ40d multimeter (Hach, USA), respectively. Several pieces of both membranes were used to conduct the experiments and to ensure the reproducibility of results. Moreover, the experiments were conducted by different operators and, therefore, the experimental data presented in the manuscript are the mean value of at least three measurements. For all experimental solute concentrations, there was very good reproducibility among different samples, with the standard deviations being lower than 10% of the average rejections.
2.3. Modelling
Membrane efficiency was evaluated by determining the permeate flux, Jv, and the observed solute rejection, , as follows:
| (1) |
| (2) |
where is the permeability coefficient, the effective transmembrane pressure calculated from the applied transmembrane pressure and differences in the osmotic pressure of the retentate and the permeate side, and and the solute concentration of the permeate and feed solution, respectively.
The observed solute rejections were fitted by the DSPM-DE coupled with the thin-film theory, which considered the presence of the concentration polarization layer in the rejection chamber. Table 2 summarises the equations of this mathematical model, which considers electroneutrality conditions at the solution-membrane interface and inside the membrane pores. It is assumed that the effective membrane charge density, , is constant at all points inside the membrane.
Table 2.
- Equations of the DSPM-DE used in this study.
| Solute flux in the solution-membrane interface (polarization layer) | |
| (T1) | |
| The mass-transfer coefficient in the polarization layer [38] | |
| (T2) | |
| Partitioning equation | |
| (T3) | |
| Extended Nernst-Planck equation for simulating solute transport through the membrane | |
| (T4) | |
| The potential gradient inside the pores | |
| (T5) | |
| Electroneutrality in the solution-membrane interface | |
| (T6) | |
| Electroneutrality inside the membrane pores | |
| (T7) | |
| Solute hindrance factor for convection | |
| (T8) | |
| Solute pore diffusion coefficient | |
| (T9) | |
| Rejection of uncharged solutes | |
| (T10) | |
All equations were implemented in Mathematica® (Wolfram Research), and differential equations were numerically solved over the membrane thickness rather than by considering the linear profile of the solute concentration inside the pores. The model parameters that provided the optimal fit to the experimental solute rejections were determined by minimising the least squares objective function:
| (3) |
where and are the experimental and calculated model solute rejections, respectively, and m the number of transmembrane pressures tested for any feed solution.
2.4. Diananofiltration modelling
The diafiltration process is based on the dilution of feed solution with pure water while the permeate stream is removed from the system. In the continuous mode, the general differential mass balance for a given solute s can be written as [39]:
| (4) |
where is the feed volume, is the solute concentration in the feed tank and is the permeate flow. By introducing Eq. (2) into Eq. (4), the differential mass balance can be rewritten as:
| (5) |
As the feed volume is constant and assuming that observed rejection and permeate flow are constant during the experiment, the concentration in the feed vessel is obtained by integrating Eq. (5) with the initial condition when :
| (6) |
Eq. (6) can be rewritten by introducing the diafiltration volume (DV), which is defined as the ratio between permeate volume and feed volume ():
| (7) |
3. Results and discussion
3.1. Water permeate flux as a function of the feed pH
The water permeate flux was measured at different transmembrane pressures and feed pH values. As shown in Fig. 1, the relationship between the water permeate flux and transmembrane pressure was linear, and the permeability coefficient was easily calculated from the slope of the line for both membranes. As expected from the MWCO values, the MPF-36 membrane showed a higher water permeate flux than the Desal 5DK membrane. Furthermore, the water permeate flux depended on the feed pH, especially for MPF-36 membrane. The maximum permeate flux was observed at pH range 6.5–7 for MPF-36 and pH range 4–4.5 for Desal 5DK, while the water flux decreased at acidic and alkaline pH values. This pH-dependence of the permeate flux indicated that the interaction between the membrane and solution was modified by the proton concentration of the feed. These results are in line with those of other studies showing a slight peak of the permeate flux at pH 5, where it was expected to have uncharged membrane pores (following the zeta-potential measurements) for a fully aromatic thin-film composite membrane [40].
Fig. 1.
Water permeate flux as a function of transmembrane pressure and the feed pH for the two membranes.
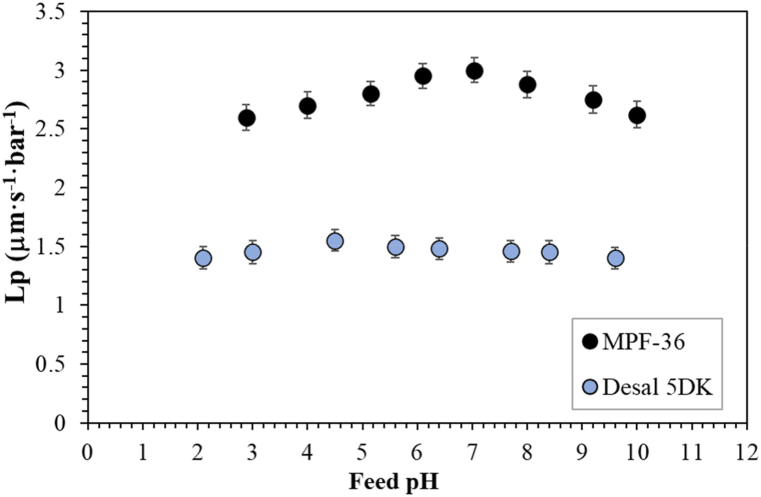
The water permeability coefficient was calculated from Eq. (1) and the effective transmembrane pressure was set equal to the applied transmembrane pressure. Fig. 2 shows the pH-dependence of the water permeability coefficient for both membranes. For the MPF-36 membrane, the calculated permeability coefficient was 2.91·10−6 m s−1 bar−1 at pH 9.2. This increased to the maximum value of 2.96·10−6 m s−1 bar−1 at pH 6.5 and then decreased at a lower feed pH. When the feed pH was fixed close to 3, the permeability coefficient (2.52·10−6 m s−1 bar−1) was reduced by14.9% of the maximum value. A similar trend was observed for the Desal 5DK membrane, but the maximum water permeability coefficient was obtained at pH 4.5 (1.59·10−6 m s−1 bar−1) and was reduced by 9.6% and 5.7% for pH 2.1 and 7.0, respectively. This pH-dependence of the permeate flux can be attributed to a possible conformational change of the cross-linked membrane surface that may increase pore size or induce changes in the apparent water permeability due to electroviscous effects [40].
Fig. 2.
Calculated water permeability coefficient as a function of the feed pH for the two nanofiltration membranes. Error bars represent 95% confidence limits.
3.2. Glucose rejection as a function of the feed pH
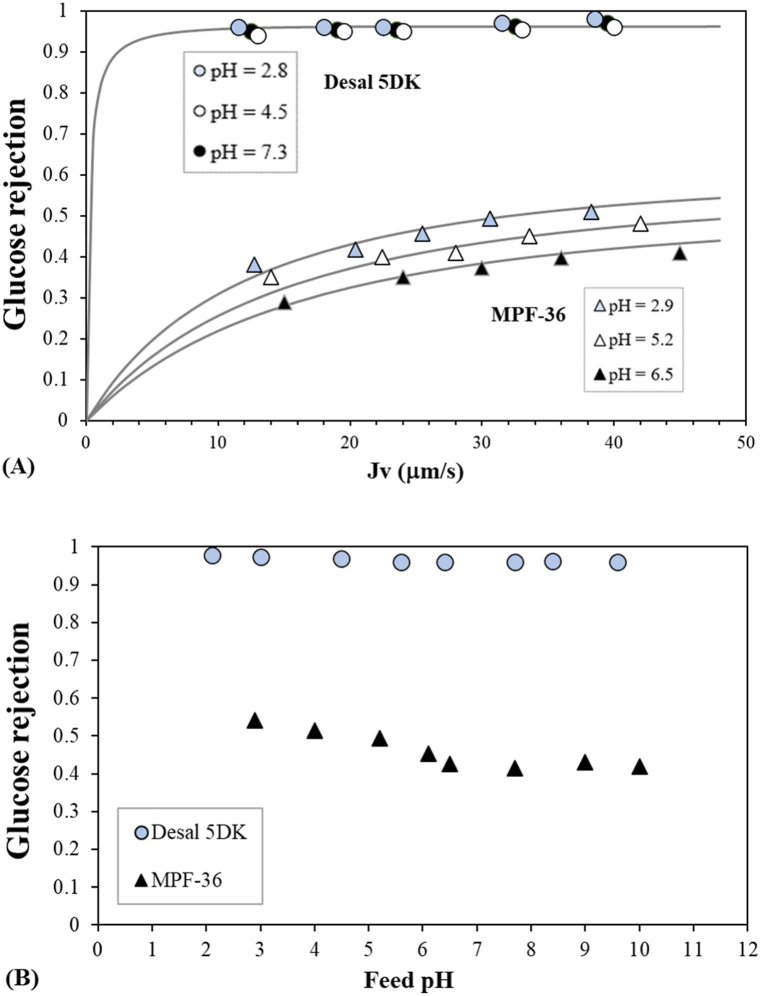
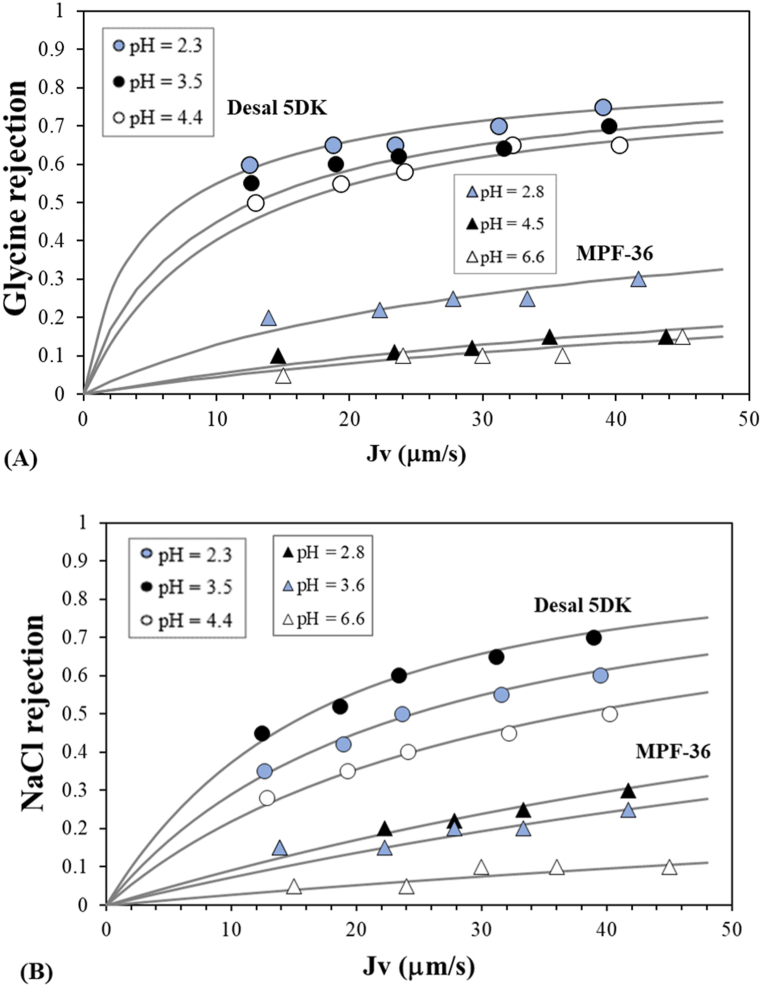
The evaluation of membrane pore size, following the DSPM-DE, was undertaken by assessing glucose rejection. As the glucose molecule is an uncharged molecule, its rejection is unaltered by electrostatic effects [41]. Glucose rejection at three different feed pH values as a function of the permeate flux is shown in Fig. 3 for the two membranes. The rejection increased with the permeate flux (and so with transmembrane pressure), and the limiting value was not achieved for the MPF-36 membrane. When the permeate flux increases, the permeated water flow increases and the solute concentration in the permeate stream decreases. Then, following Eq. (2), the solute rejection increases as the solute feed concentration is constant.
Fig. 3.
Glucose rejection as a function of (A) the permeate flux at different feed pH values for the two membranes and (B) feed pH at fixed permeate flux of 40 μm s−1. Symbols correspond to the experimental data and lines correspond to the fitted data. Circles represent the Desal 5DK membrane and triangles theMPF-36 membrane.
For the MPF-36 membrane, glucose rejection increased with decreasing feed pH, i.e., from 0.42 to 0.55 at pH 10 and 2.9, respectively, for a 10 mM glucose solution and permeate flux of 40 μm s−1. The main increase in glucose rejection was observed when moving from a neutral to an acidic pH, while a slight increase was observed when moving to an alkaline pH. Glucose rejection reached a minimum at a neutral pH, which is in accordance with the maximum value of the water permeability coefficient. Thus, the variations in membrane performance with feed pH may indicate a conformational modification in the structure of the membrane surface, as glucose molecule and water physical characteristics are assumed to be independent of pH. For instance, the low proton concentration at neutral pH could indicate a modification of the structural properties of the membrane polymer that could suggest a variation in membrane pore radius. This phenomenon is usually called membrane swelling [42,43]. However, the Desal 5DK membrane showed an experimental glucose rejection close to 1, with very slight variation with regard to the feed pH values, due to the considerable steric exclusion.
The experimental glucose rejections were fitted with the equation (T10), which is based on the diffusion and convection mechanism [44,45], by varying the pore radius until the least squares objective function (Eq. (3)) was minimised. Fig. 3 also shows the fitting of the data to the experimental values. Glucose rejections for the Desal 5DK membrane were fitted with a membrane pore radius of 0.45 nm, although different membrane pore radii can also fit the experimental rejection with good correlation. Oatley et al. [36] estimated a membrane pore radius of 0.45 nm by fitting the glucose and glycine rejections simultaneously, however the glucose rejections were underestimated, and a lower membrane pore radius may provide a better fit to the experimental data. Bandini et al. [46] analysed the fructose rejection at different feed pH values and they fitted all experimental rejections with a membrane pore radius of 0.41 nm and they postulated that the neutral rejections may be affected by the changes in membrane pore radius and/or solute size. Therefore, the membrane pore radius cannot be determined properly with glucose rejection for membranes with a low MWCO such as the Desal 5DK membrane. In the following subsection, we propose the use of amino acid molecules to establish nanofiltration performance in a specific pH range.
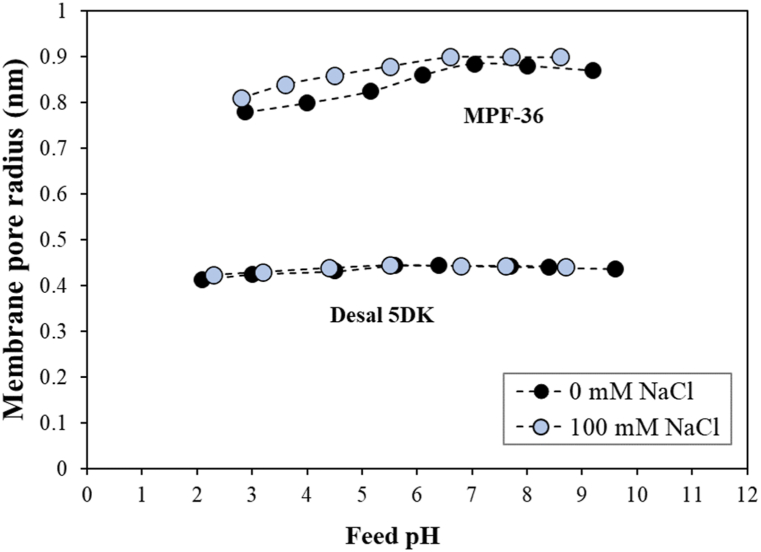
On the other hand, a high correlation was observed between the fitted and experimental glucose rejection for the MPF-36 membrane (Fig. 3). The variation in glucose rejection was due to the change in membrane pore radius as a function of feed pH. As shown in Fig. 4, the decrease in the membrane pore radius at alkaline pH values was less significant than that at acidic pH values. Thus, the estimated membrane pore radius at pH 6.5, when the effective membrane charge is zero, was 0.89 nm, and was 0.78 nm, 0.82 nm and 0.87 nm at pH 2.9, 5.2 and 9.2, respectively. Membrane swelling is one mechanism that can explain the changes in the pore radius with feed pH [47], although there is still no physical evidence. Fig. 4 also shows the membrane pore radius for Desal 5DK. In this case, no significant difference in membrane pore radius is observed with feed pH, as observed by Bandini et al. [46] at different temperatures.
Fig. 4.
Membrane pore radius for the two membranes as a function of the feed pH and NaCl concentration. Membrane pore radius for the MPF-36 membrane was calculated from glucose solutions and for the Desal 5DK membrane from glycine solution.
3.3. Rejection of amino acid molecules as a function of the feed pH in single solute solutions
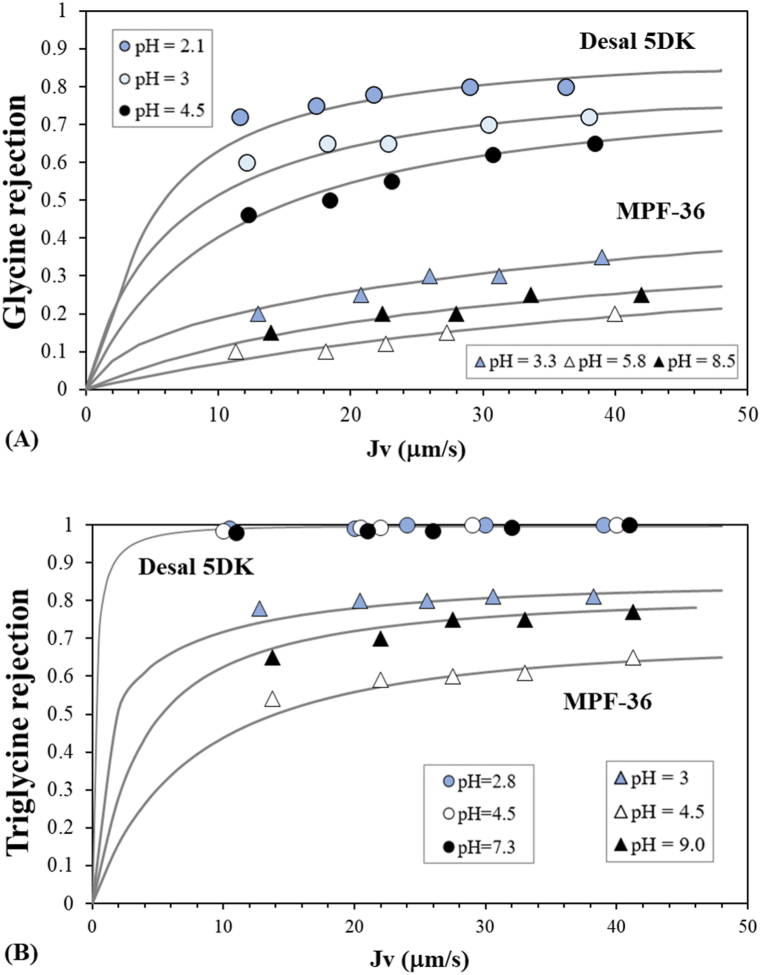
Fig. 5 shows the experimental and calculated glycine and triglycine rejections for the two membranes as a function of the permeate flux at two feed pHs. The results at all feed pHs are presented in Figs. S1, S2 and S3 of supplementary information. In all cases, the rejection increased permeate flux and varied with the feed pH. Notice that triglycine rejection for Desal 5DK membrane is close to 1 for all feed pH values, as could be expected from the glucose rejections. Calculations were conducted with the membrane pore radius estimated previously with the glucose rejection. The fitting curves at very acid and alkaline pH values were adjusted considering an effective membrane charge. There was good agreement between the calculated and experimental data of both solutes at all the feed pH values. Conversely, the experimental glycine rejection for the Desal 5DK membrane was fitted by matching the calculated curve to find the membrane pore radius for each solution, since glucose rejection does not permit the assessment of the appropriate value. Good agreement was observed between the calculated and experimental data, as shown in Fig. 5, Fig. S1 and Fig. S2. The calculated membrane pore radius shows a pH-dependence, as shown in Fig. 4, where a very slight decrease in the membrane pore radius is observed with feed pH. The highest value was 0.44 nm at the membrane IEP and it decreased to 0.423 nm at pH 2.3 and to 0.437 nm at pH 9.6. Therefore, the membrane pore radius fitted with glycine rejection was slightly lower than the calculated value previously reported in the literature. The reported membrane pore radius for the Desal 5DK membrane ranged between 0.44 and 0.487 nm when glucose and glycerol rejections were used for the estimation [17,36,48,49].
Fig. 5.
Solute rejection in single solute solutions for the two membranes as a function of the permeate flux and feed pH: (A) glycine rejection and (B) triglycine rejection. Symbols correspond to the experimental data and lines correspond to the fitted data. Circles represent the Desal 5DK membrane and triangles the MPF-36 membrane.
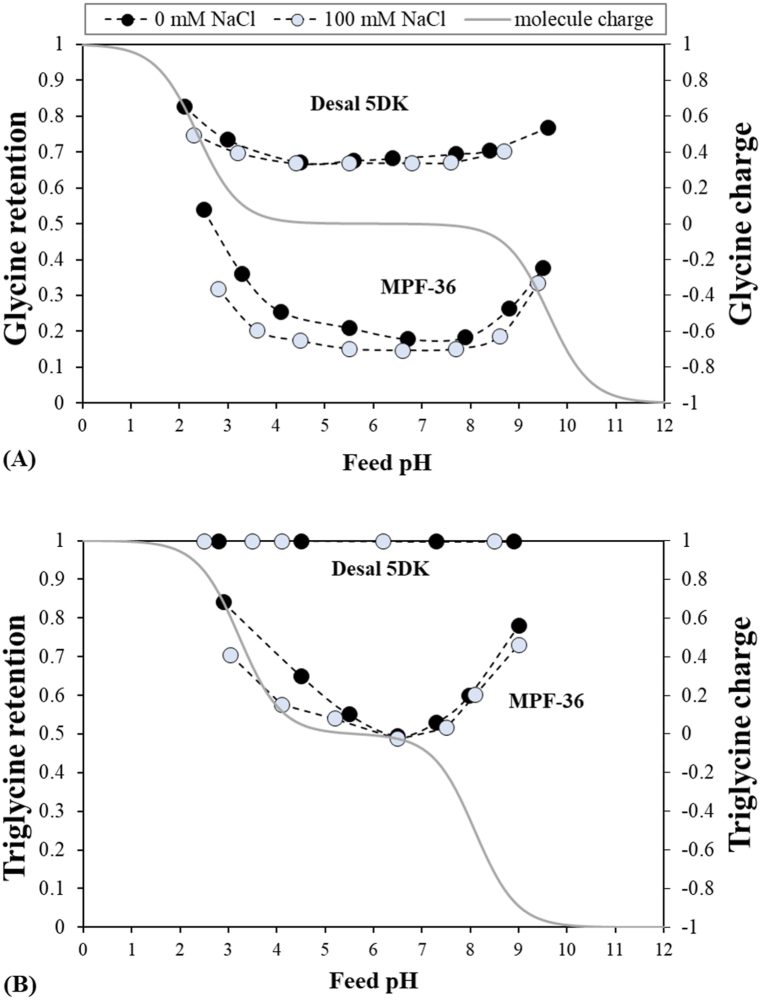
The effects of feed pH on the rejection at a fixed permeate flux of 40 μm s−1 are better visualized in Fig. 6. The figure also presents the evolution of the electric charge of the solutes. The lowest glycine rejection was observed at the corresponding membrane IEP, being 0.19 at pH 6.5, and 0.68 at pH 4.5 for the MPF-36 and Desal 5DK membranes, respectively. When the glycine zwitterion was predominant, glycine rejection showed a slight dependence on the feed pH. This was more visible in the MPF-36 membrane. For the two membranes, when the feed pH dropped to acidic values, glycine rejection rose to 0.35 at pH 3.3 and 0.72 at pH 3 for the MPF-36 and Desal 5DK membranes, respectively. Similarly, when the feed pH rose to alkaline values, glycine rejection increased to 0.25 at pH 8.5 and 0.68 at pH 8.4 for the MPF-36 and Desal 5DK membranes, respectively. This increase in rejection may be due to the repulsion between the charged amino groups or the charged carboxylic groups and the effective membrane charge [50,51].
Fig. 6.
Glycine and triglycine rejections for (A) the MPF-36 membrane and (B) the Desal 5DK membrane as a function of the feed pH and the NaCl concentration corresponding to a permeate flux of 40 μm s−1 for the two membranes, and electrical solute charge as a function of the feed pH (represented by the grey line). Discontinuous lines are presented only to show the evolution of the rejections.
Triglycine rejections are also shown in Fig. 6. Notice that triglycine rejection for the Desal 5DK membrane is close to 1 for all feed pH values, as it could be expected from the glucose rejections. Like glycine rejection, triglycine rejection for MPF-36 membrane showed a high pH-dependence, mainly due to the zwitterion predominating at a lower pH range (from 4.5 to 7.2). However, as observed with glucose rejection, the rejection of zero-charged triglycine molecule increased with a decrease in the feed pH. This may be due to some structural changes in the membrane surface when the proton concentration increased, as zero-charged triglycine rejection is unaltered by modifications in electrostatic interactions. Thus, these variations with feed pH could be due to a decrease in the membrane pore radius. The lowest triglycine rejection was 0.48 at pH 6.7, rising to 0.55 at pH 5.5 and to 0.62 at pH 4.6. This confirmed the validity of the membrane pore radii estimated previously with the glucose molecule. As expected, at very acidic and very alkaline feed pH values, Donnan exclusion became more notably and triglycine rejections increased significantly to 0.83 and 0.78 at pH 2.9 and 9.0, respectively.
3.4. Effect of feed pH on rejection of solutes in binary solutions
The nanofiltration performance of the glycine and triglycine was analysed in presence of 100 mM NaCl. Fig. 7 shows the glycine and NaCl rejections in binary solutions as a function of the permeate flux at three different feed pHs for the two membranes. Similarly, Fig. 8 shows the triglycine and NaCl rejection in binary solutions. All rejections are shown in Figs. S4, S5, S6 and S7 in the supplementary information. Comparing Fig. 5, Fig. 7, glycine rejection can be seen to decrease slightly with the NaCl concentration. For the Desal 5DK membrane, glycine rejection decreased only at pH 2, from 0.82 to 0.75, and it was almost constant at the rest of feed pHs. Fig. 6 also shows the glycine and triglycine rejections for binary solutions at a permeate flux of 40 μm s−1, which it is useful to evaluate the effect of salt. Thus, notable variations of glycine rejection were observed with NaCl concentration for the MPF-36 membrane at acidic and basic pHs (Fig. 6): from 0.35 to 0.20 at pH 3.3 and from 0.25 to 0.21 at pH 8.5 for a permeate flux of 40 μm s−1. Similarly, triglycine rejection for the MPF-36 membrane (Fig. 6) decreased from 0.83 to 0.70 at pH 3 and from 0.78 to 0.72 at pH 9 in presence of NaCl. Nevertheless, no significant change in the three solute rejections was observed at pH 4.5 and 6.5 for the Desal 5DK and the MPF-36 membranes, respectively. Likewise, NaCl rejection also shows pH-dependence and the lowest rejection values were obtained, being 0.1 at pH 6.6 and 0.5 at pH 4.5 for the MPF-36 and Desal 5DK membranes, respectively. At acidic and basic pHs, NaCl rejection increased like glycine and triglycine rejection.
Fig. 7.
Rejection of solutes in glycine-NaCl binary solutions as a function of the permeate flux and feed pH: (A) glycine rejection and (B) NaCl rejection. Symbols correspond to the experimental data and lines correspond to the fitted data. Circles represent the Desal 5DK membrane and triangles the MPF-36 membrane.
Fig. 8.
Rejection of solutes in triglycine-NaCl binary solutions as a function of the permeate flux and feed pH: (A) triglycine rejection and (B) NaCl rejection. Symbols correspond to the experimental data and lines correspond to the fitted data. Circles represent the Desal 5DK membrane and triangles the MPF-36 membrane.
The experimental glycine-NaCl and triglycine-NaCl rejections from the binary solutions were fitted by the DSPM-DE. First, the dielectric pore constant was estimated with NaCl rejection at the membrane IEP of each membrane, when the effective membrane charge is considered to be zero and the Donnan potential is ignored. Under this condition, the mechanism that best explains the NaCl rejection values is dielectric exclusion. The calculated dielectric pore constant was 69.8 at pH 6.5 for the MPF-36 membrane and 49.6 at pH 4.5 for the Desal 5DK membrane, which were, respectively, 11% and 43% lower than the dielectric constant of pure water. A similar behaviour was observed by Oatley et al. [37], who found a reduction of more than 50% in the dielectric constant of the pore with respect to that of the bulk solution (10 mM NaCl) for the Desal 5DK membrane. Thereafter, the membrane pore radius was calculated by matching the experimental and calculated glycine and triglycine rejections for binary solutions in the pH range from 4.5 to 7.2. The calculated membrane pore radii are shown in Fig. 4. There was an increase in the membrane pore radius with the presence of NaCl, especially for the MPF-36 membrane at acidic pH. For instance, the membrane pore radius increased from 0.8 nm to 0.86 nm at pH 4 and from 0.87 to 0.9 at pH 7. One of the mechanisms that might explain this phenomenon is the swelling of the membrane matrix, which leads to increases in the membrane pore size. Alternatively, pore size distribution and a variation in the solute Stokes radius in the presence of salt have also been proposed to describe this behaviour [29,52]. The membrane pore radii for the Desal 5DK membrane can be considered as almost independent of the NaCl concentration, at least for the relatively low NaCl concentration tested.
Lastly, the NaCl rejections at the other feed pH values and glycine and triglycine rejections at acidic and basic pHs were fitted by adjusting the effective membrane charge and using the pH-dependence of the membrane pore radii as well as the membrane pore dielectric constant established at the membrane IEP [36,53]. The evolution of the effective membrane charge as a function of the feed pH for the two membranes is shown in Fig. 9. The effective membrane charge values were smaller for the membrane with the lowest MWCO (Desal 5DK) at all the feed pH values. This is due to the more significant dielectric exclusion (lower pore dielectric constant) observed for the small-scale membrane pore radii. Similar to zeta-potential measurements, the effective membrane charge of both membranes is positively and negatively charged at lower and higher pH values than the membrane IEP, respectively [12,36]. For instance, the effective membrane charge was 81.1 mol m−3 at pH 3.6 and 36.2 mol m−3 at pH 5.5 for the MPF-36 membrane, and −10.3 mol m−3 at pH 5.3 and −34.1 mol m−3 at pH 7.6 for the Desal 5DK membrane. Moreover, the pH-dependence of the effective membrane charge differed at acidic and alkaline feed pH values, with higher values found in the alkaline solutions. These values are in agreement with those reported in the literature. For instance, Bandini et al. [35] estimated the effective membrane charge values of −3.9 mol m−3, −6.8 mol m−3 and −13.6 mol m−3 at pH 4.5, 5.3 and 6.5, respectively, for 20 mol m−3 NaCl. The slight difference with regard to our results is due to the presence of a higher NaCl concentration (100 mol m−3).
Fig. 9.
Effective membrane charge as a function of the feed pH for the two membranes. The values were calculated by fitting NaCl rejection in the binary solutions with the DSPM-DE.
3.5. Diananofiltration calculations
Comparing the rejections of triglycine and NaCl for the two membranes at a permeate flux of 40 μm s−1 (Fig. 6), triglycine rejections in binary solutions were always at least 40% higher than NaCl rejections at all the feed pH values. Therefore, the separation (or purification) of the binary solution formed from triglycine and NaCl can be achieved with the two membranes. The purification step may be conducted in a continuous diafiltration mode (also called diananofiltration), which consists of constantly adding water in order to maintain a constant feed volume that allows the concentration of solutes in the feed tank and prevents membrane fouling [54,55]. Other authors have proposed purifying the concentration mode, which presents higher membrane fouling [56]. We conducted a simulation of the continuous diananofiltration process following Eq. (7).
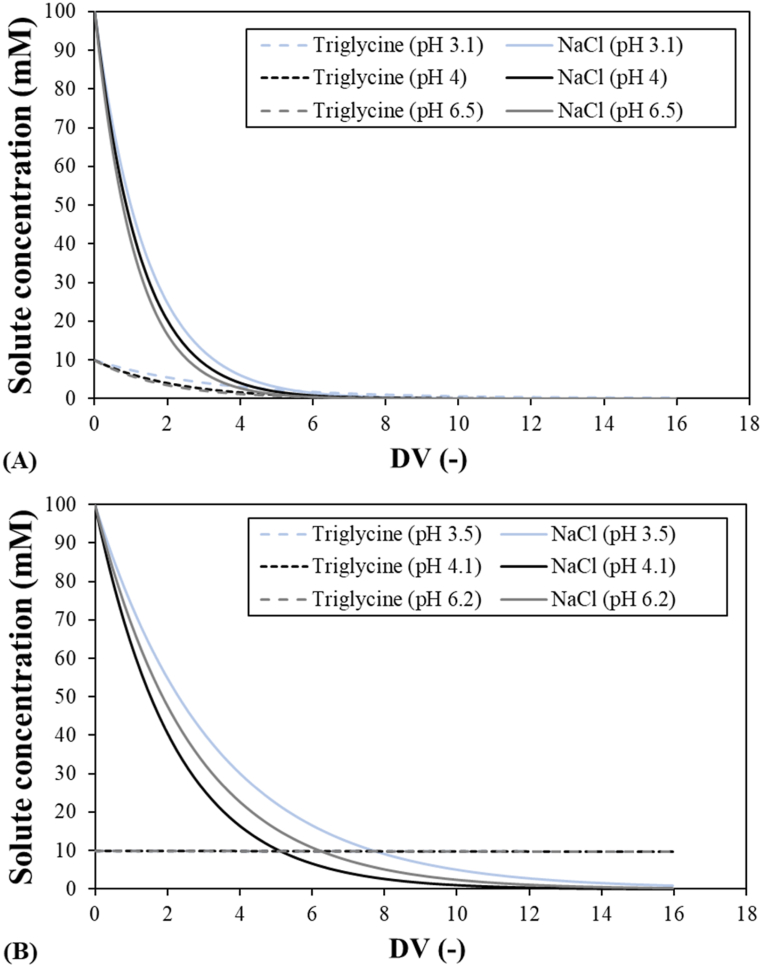
Diananofiltration calculations of binary solutions were conducted at three feed pHs with the solute rejections corresponding to 40 μm s−1 (Table 3) by assuming that rejections are constant during the process. Fig. 10 shows the diananofiltration calculations for the two membranes. It is observed that only the desalination of triglycine is obtained with the Desal 5 DK membrane. The best separation conditions were obtained at pH 4, when triglycine was the majority component in the feed tank from a diafiltration volume of 4.8 and the mass fraction of 95% was reached at a diafiltration volume of 14.1. Conversely, the collected permeate is mainly composed by NaCl with a total concentration of 9.8 mol m−3 and a mass fraction of 99.8% at this diafiltration volume. Similar results were found at all feed pHs, as the solute rejections are very similar. The triglycine mass fraction of 95% is obtained at diafiltration volumes of 20.2 and 17.6 at pH 3 and 6.5, respectively. Consequently, future work will consist of studying experimentally the diananofiltration of triglycine and extending the analysis to other tripeptides.
Table 3.
Solute rejections for diananofiltration calculations in binary solutions at 40 μm s−1 for the two membranes.
| pH | Triglycine rejection | NaCl rejection | |
|---|---|---|---|
| MPF-36 | 3.1 | 0.71 | 0.31 |
| 4 | 0.55 | 0.22 | |
| 6.5 | 0.48 | 0.098 | |
| Desal 5DK | 3.5 | 0.998 | 0.71 |
| 4.1 | 0.999 | 0.51 | |
| 6.2 | 0.997 | 0.62 |
Fig. 10.
Calculations in a continuous diananofiltration mode for (A) the MPF-36 membrane and (B) the Desal 5DK membrane. Triglycine and NaCl rejections in binary solutions at three different feed pHs and 40 μm s−1 (Table 3).
4. Conclusions
Two commercial nanofiltration membranes with different MWCO were experimentally characterised by applying the well-known DSPM-DE based on variations in the feed pH. The ability of the two membranes to purify amino acid binary solutions in the presence of NaCl was also evaluated.
The water permeability coefficient for both membranes showed pH-dependence. For the MPF-36 membrane, the maximum water permeability value was reached at pH 7 and it decreased significantly at higher and lower pHs. For its part, the Desal 5DK membrane showed lower pH-dependence, leading a maximum value at pH 4.5.
The rejection of all solutes depended on the feed pH, and showed minimum values at the pH at which water permeability was maximum. Glucose rejection increased with the decrease in feed pH and was almost constant at basic pHs for the MPF-36 membrane, and the fitting curves with the DSPM-DE allowed the calculation of the membrane pore radius, which showed a pH-dependency. In contrast, the estimated membrane pore radius for the Desal 5 DK membrane was inconsistent, because glucose rejection was close to 1 for all pHs. Glycine and triglycine rejections showed a pH-dependency with a u-shaped curve, leading to similar rejection values at acidic and basic pHs. Even for the zwitterion species, the glycine and triglycine rejections increased with feed pH. In binary solutions, glycine and triglycine rejections decreased in the presence of NaCl for the two membranes, especially under acidic pH conditions. Following the DSPM-DE, the variations in rejection with feed pH and NaCl concentration were attributed to changes in membrane pore radius, which decreased at acidic pHs.
The desalination of triglycine binary solutions was studied by the simulation of continuous diananofiltration. The calculations showed that only the Desal 5 DK can desalt the triglycine reaching a mass fraction of 95% by adding a volume of pure water 14.1 times the feed volume.
Author contribution statement
Shirin Shahgodari, Jordi Labanda, Joan Llorens: Conceived and designed the experiments; Performed the experiments; Analysed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
The authors are grateful to the Spanish “Ministerio de Economia y Competitividad” (project CTM2016-76275-R) for funds received to carry out this study.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e16797.
Nomenclature
Roman symbols
- Ak
Membrane porosity (−)
- Cf,s
Feed solute concentration (mol m−3)
- Cm,s
Solute concentration inside the membrane (mol m−3)
- Cp,s
Permeate solute concentration (mol m−3)
- Ds
Bulk solute Diffusivity (m2·s−1)
- Ds,p
Solute diffusivity inside the pores (m2·s−1)
- DV
Diafiltration volume (−)
- F
Faraday constant (96,485 C mol−1)
- Jv
Permeate flux (m s−1)
- kB
Boltzmann constant (1.38066 10−23 J K−1)
- Ks,c
Solute convection hindrance coefficient (−)
- Ks,D
Solute diffusion hindrance coefficient (−)
- LP
Membrane permeability coefficient (m·s−1·Pa−1)
- Rg
Gases constant (8.31 J K−1 mol−1)
- Rs
Observed solute rejection (−)
- RG
Observed uncharged solute rejection (−)
- rs
Solute radius (m)
- rp
Membrane pore radius (m)
- Sy
Least squares objective function (−)
- T
Absolute temperature (K)
- Vf
Feed volume (m3)
- Vp
Permeate volume (m3)
- Xd
Membrane volumetric charge density (mol·m−3)
- x
- Axial coordinate (m)
- zs
Solute electrical charge(−)
Greek symbols
- ΔPe
Effective transmembrane pressure (Pa)
- Δx
Membrane thickness (m)
- εo
vacuum dielectrical constant (8.85 10 −12 J-1 C2 m−1)
- εb
Bulk dielectrical constant (−)
- εp
Pore dielectrical constant (−)
- θ
Recovery (−)
- ΦD,s
Donnan exclusion coefficient (−)
- ΦDE,s
Dielectrical exclusion coefficient (−)
- ΦS,s
Steric hindrance coefficient (−)
- Ψm
Electrical potential in the membrane (V)
- ΨD
Donnan potential (V)
Appendix A. Supplementary data
The following is the Supplementary data to this article.
References
- 1.Castro-Muñoz R., Barragán-Huerta B.E., Fíla Vlastimil, Pierre, Denis C., Ruby-Figueroa R. Current role of membrane technology: from the treatment of agro-industrial by-products up to the valorization of valuable compounds. Waste and Biomass Valorization. 2018;9:513–529. doi: 10.1007/s12649-017-0003-1. [DOI] [Google Scholar]
- 2.Marson G.V., Belleville M.-P., Lacour S., Dupas Hubinger M. 2020. Membranes Membrane Fractionation of Protein Hydrolysates from By-Products: Recovery of Valuable Compounds from Spent Yeasts. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Amorim M., Pereira J.O., Gomes D., Pereira C.D., Pinheiro H., Pintado M. Nutritional ingredients from spent brewer's yeast obtained by hydrolysis and selective membrane filtration integrated in a pilot process. J. Food Eng. 2016;185:42–47. doi: 10.1016/J.JFOODENG.2016.03.032. [DOI] [Google Scholar]
- 4.Emin C., Kurnia E., Katalia I., Ulbricht M. Polyarylsulfone-based blend ultrafiltration membranes with combined size and charge selectivity for protein separation. Sep. Purif. Technol. 2018;193:127–138. doi: 10.1016/J.SEPPUR.2017.11.008. [DOI] [Google Scholar]
- 5.Saidi S., Deratani A., Ben Amar R., Belleville M.P. Fractionation of a tuna dark muscle hydrolysate by a two-step membrane process. Sep. Purif. Technol. 2013;108:28–36. doi: 10.1016/J.SEPPUR.2013.01.048. [DOI] [Google Scholar]
- 6.Vandanjon L., Johannsson R., Derouiniot M., Bourseau P., Jaouen P. Concentration and purification of blue whiting peptide hydrolysates by membrane processes. J. Food Eng. 2007;83:581–589. doi: 10.1016/J.JFOODENG.2007.03.040. [DOI] [Google Scholar]
- 7.Brás T., Guerra V., Torrado I., Lourenço P., Carvalheiro F., Duarte L.C., Neves L.A. Detoxification of hemicellulosic hydrolysates from extracted olive pomace by diananofiltration. Process Biochem. 2014;49:173–180. doi: 10.1016/J.PROCBIO.2013.09.017. [DOI] [Google Scholar]
- 8.Nguyen D.T.N.N., Lameloise M.L., Guiga W., Lewandowski R., Bouix M., Fargues C. Optimization and modeling of diananofiltration process for the detoxification of ligno-cellulosic hydrolysates - study at pre-industrial scale. J. Membr. Sci. 2016;512:111–121. doi: 10.1016/J.MEMSCI.2016.04.008. [DOI] [Google Scholar]
- 9.Brás T., Rosa D., Gonçalves A.C., Gomes A.C., Brazinha C., Neves L.A., Duarte M.F., Crespo J.G. Fractionation of Cynara cardunculus ethanolic extracts using diananofiltration. Sep. Purif. Technol. 2021;256 doi: 10.1016/J.SEPPUR.2020.117856. [DOI] [Google Scholar]
- 10.Domingos J.M.B., Teixeira A.R.S., Dupoiron S., Allais F., Lameloise M.L. Simultaneous recovery of ferulic acid and sugars from wheat bran enzymatic hydrolysate by diananofiltration. Sep. Purif. Technol. 2020;242 doi: 10.1016/J.SEPPUR.2020.116755. [DOI] [Google Scholar]
- 11.Samavati Z., Samavati A., Goh P.S., Fauzi Ismail A., Sohaimi Abdullah M. A comprehensive review of recent advances in nanofiltration membranes for heavy metal removal from wastewater. Chem. Eng. Res. Des. 2023;189:530–571. doi: 10.1016/J.CHERD.2022.11.042. [DOI] [Google Scholar]
- 12.Negaresh E., Antony A., Bassandeh M., Richardson D.E., Leslie G. Selective separation of contaminants from paper mill effluent using nanofiltration. Chem. Eng. Res. Des. 2012;90:576–583. doi: 10.1016/j.cherd.2011.08.005. [DOI] [Google Scholar]
- 13.Vyas B.B., Ray P. Preparation of nanofiltration membranes and relating surface chemistry with potential and topography: application in separation and desalting of amino acids. Desalination. 2015;362:104–116. doi: 10.1016/J.DESAL.2015.02.013. [DOI] [Google Scholar]
- 14.Mänttäri M., Pihlajamäki A., Nyström M. Effect of pH on hydrophilicity and charge and their effect on the filtration efficiency of NF membranes at different pH. J. Membr. Sci. 2006;280:311–320. doi: 10.1016/J.MEMSCI.2006.01.034. [DOI] [Google Scholar]
- 15.Bruni L., Bandini S. The role of the electrolyte on the mechanism of charge formation in polyamide nanofiltration membranes. J. Membr. Sci. 2008;308:136–151. doi: 10.1016/j.memsci.2007.09.061. [DOI] [Google Scholar]
- 16.Wu D., Martin J., Du J.R., Zhang Y., Lawless D., Feng X. Effects of chlorine exposure on nanofiltration performance of polyamide membranes. J. Membr. Sci. 2015;487:256–270. doi: 10.1016/j.memsci.2015.02.021. [DOI] [Google Scholar]
- 17.Bowen W.R., Welfoot J.S. Modelling the performance of membrane nanofiltration-critical assessment and model development. Chem. Eng. Sci. 2002;57:1121–1137. doi: 10.1016/S0009-2509(01)00413-4. [DOI] [Google Scholar]
- 18.Qin J.-J., Oo M.H., Lee H., Coniglio B. Effect of feed pH on permeate pH and ion rejection under acidic conditions in NF process. J. Membr. Sci. 2004;232:153–159. doi: 10.1016/J.MEMSCI.2003.12.010. [DOI] [Google Scholar]
- 19.Epsztein R., Shaulsky E., Dizge N., Warsinger D.M., Elimelech M. Role of ionic charge density in donnan exclusion of monovalent anions by nanofiltration. Environ. Sci. Technol. 2018;52:4108–4116. doi: 10.1021/acs.est.7b06400. [DOI] [PubMed] [Google Scholar]
- 20.Bargeman G. Recent developments in the preparation of improved nanofiltration membranes for extreme pH conditions. Sep. Purif. Technol. 2021;279 doi: 10.1016/J.SEPPUR.2021.119725. [DOI] [Google Scholar]
- 21.Szoke S., Patzay G., Weiser L. Characteristics of thin-film nanofiltration membranes at various pH-values. Desalination. 2003;151:123–129. doi: 10.1016/S0011-9164(02)00990-6. [DOI] [Google Scholar]
- 22.Luo J., Wan Y. Effects of pH and salt on nanofiltration-a critical review. J. Membr. Sci. 2013;438:18–28. doi: 10.1016/j.memsci.2013.03.029. [DOI] [Google Scholar]
- 23.Civit M., Fragua X., Guastalli A.R., Labanda J., Llorens J. Effect of pH and salt concentration on the nanofiltration of Glycine and triglycine. Procedia Eng. 2012;44:585–587. doi: 10.1016/J.PROENG.2012.08.493. [DOI] [Google Scholar]
- 24.Bowen W.R., Mohammad A.W., Hilal N. Characterisation of nanofiltration membranes for predictive purposes — use of salts, uncharged solutes and atomic force microscopy. J. Membr. Sci. 1997;126:91–105. doi: 10.1016/S0376-7388(96)00276-1. [DOI] [Google Scholar]
- 25.Déon S., Escoda A., Fievet P., Dutournié P., Bourseau P. How to use a multi-ionic transport model to fully predict rejection of mineral salts by nanofiltration membranes. Chem. Eng. J. 2012;189–190:24–31. doi: 10.1016/J.CEJ.2012.02.014. [DOI] [Google Scholar]
- 26.Fadaei F., Hoshyargar V., Shirazian S., Ashrafizadeh S.N. Mass transfer simulation of ion separation by nanofiltration considering electrical and dielectrical effects. Desalination. 2012;284:316–323. doi: 10.1016/J.DESAL.2011.09.018. [DOI] [Google Scholar]
- 27.Yaroshchuk A.E. Rejection mechanisms of NF membranes. Membr. Technol. 1998;1998:9–12. doi: 10.1016/S0958-2118(00)87465-0. [DOI] [Google Scholar]
- 28.Szymczyk A., Fievet P. Investigating transport properties of nanofiltration membranes by means of a steric, electric and dielectric exclusion model. J. Membr. Sci. 2005;252:77–88. doi: 10.1016/J.MEMSCI.2004.12.002. [DOI] [Google Scholar]
- 29.Bargeman G., Westerink J.B., Manuhutu C.F.H., ten Kate A. The effect of membrane characteristics on nanofiltration membrane performance during processing of practically saturated salt solutions. J. Membr. Sci. 2015;485:112–122. doi: 10.1016/J.MEMSCI.2015.03.039. [DOI] [Google Scholar]
- 30.Mohammad A.W., Teow Y.H., Ang W.L., Chung Y.T., Oatley-Radcliffe D.L., Hilal N. Nanofiltration membranes review: recent advances and future prospects. Desalination. 2015;356:226–254. doi: 10.1016/J.DESAL.2014.10.043. [DOI] [Google Scholar]
- 31.Bandini S. Modelling the mechanism of charge formation in NF membranes: theory and application. J. Membr. Sci. 2005;264:75–86. doi: 10.1016/J.MEMSCI.2005.03.055. [DOI] [Google Scholar]
- 32.Hagmeyer G., Gimbel R. Modelling the rejection of nanofiltration membranes using zeta potential measurements. Sep. Purif. Technol. 1999;15:19–30. doi: 10.1016/S1383-5866(98)00050-1. [DOI] [Google Scholar]
- 33.Saliha B., Patrick F., Anthony S. Investigating nanofiltration of multi-ionic solutions using the steric, electric and dielectric exclusion model. Chem. Eng. Sci. 2009;64:3789–3798. doi: 10.1016/J.CES.2009.05.020. [DOI] [Google Scholar]
- 34.Sabaté J., Labanda J., Llorens J. Influence of coion and counterion size on multi-ionic solution nanofiltration. J. Membr. Sci. 2009;345 doi: 10.1016/j.memsci.2009.09.013. [DOI] [Google Scholar]
- 35.Bandini S., Drei J., Vezzani D. The role of pH and concentration on the ion rejection in polyamide nanofiltration membranes. J. Membr. Sci. 2005;264:65–74. doi: 10.1016/j.memsci.2005.03.054. [DOI] [Google Scholar]
- 36.Oatley D.L., Llenas L., Aljohani N.H.M., Williams P.M., Martínez-Lladó X., Rovira M., de Pablo J. Investigation of the dielectric properties of nanofiltration membranes. Desalination. 2013;315:100–106. doi: 10.1016/J.DESAL.2012.09.013. [DOI] [Google Scholar]
- 37.Oatley D.L., Llenas L., Pérez R., Williams P.M., Martínez-Lladó X., Rovira M. Review of the dielectric properties of nanofiltration membranes and verification of the single oriented layer approximation. Adv. Colloid Interface Sci. 2012;173:1–11. doi: 10.1016/j.cis.2012.02.001. [DOI] [PubMed] [Google Scholar]
- 38.Sabaté J., Labanda J., Llorens J. Influence of coion and counterion size on multi-ionic solution nanofiltration. J. Membr. Sci. 2009;345:298–304. doi: 10.1016/J.MEMSCI.2009.09.013. [DOI] [Google Scholar]
- 39.Awais Ashraf M., Li X., Wang J., Guo S., Xu B.H. DiaNanofiltration-based process for effective separation of Li+ from the high Mg2+/Li+ ratio aqueous solution. Sep. Purif. Technol. 2020;247 doi: 10.1016/J.SEPPUR.2020.116965. [DOI] [Google Scholar]
- 40.Childress A.E., Elimelech M. Relating nanofiltration membrane performance to membrane charge (electrokinetic) characteristics. Environ. Sci. Technol. 2000;34:3710–3716. doi: 10.1021/es0008620. [DOI] [Google Scholar]
- 41.Tonova K., Lazarova M., Dencheva-Zarkova M., Paniovska S., Tsibranska I., Stanoev V., Dzhonova D., Genova J. Separation of glucose, other reducing sugars and phenolics from natural extract by nanofiltration: effect of pressure and cross-flow velocity. Chem. Eng. Res. Des. 2020;162:107–116. doi: 10.1016/J.CHERD.2020.07.030. [DOI] [Google Scholar]
- 42.Luo J., Ding L. Influence of pH on treatment of dairy wastewater by nanofiltration using shear-enhanced filtration system. Desalination. 2011;278:150–156. doi: 10.1016/J.DESAL.2011.05.025. [DOI] [Google Scholar]
- 43.Nilsson M., Trägårdh G., Östergren K. The influence of pH, salt and temperature on nanofiltration performance. J. Membr. Sci. 2008;312:97–106. doi: 10.1016/J.MEMSCI.2007.12.059. [DOI] [Google Scholar]
- 44.Bargeman G., Westerink J.B., Guerra Miguez O., Wessling M. The effect of NaCl and glucose concentration on retentions for nanofiltration membranes processing concentrated solutions. Sep. Purif. Technol. 2014;134:46–57. doi: 10.1016/J.SEPPUR.2014.07.025. [DOI] [Google Scholar]
- 45.Almazán J.E., Romero-Dondiz E.M., Rajal V.B., Castro-Vidaurre E.F. Nanofiltration of glucose: analysis of parameters and membrane characterization. Chem. Eng. Res. Des. 2015;94:485–493. doi: 10.1016/J.CHERD.2014.09.005. [DOI] [Google Scholar]
- 46.Bandini S., Morelli V. Effect of temperature, pH and composition on nanofiltration of mono/disaccharides: experiments and modeling assessment. J. Membr. Sci. 2017;533:57–74. doi: 10.1016/J.MEMSCI.2017.03.021. [DOI] [Google Scholar]
- 47.Freger V. Swelling and morphology of the skin layer of polyamide composite membranes: an atomic force microscopy study. Environ. Sci. Technol. 2004;38:3168–3175. doi: 10.1021/es034815u. [DOI] [PubMed] [Google Scholar]
- 48.Bargeman G., Vollenbroek J.M., Straatsma J., Schroën C.G.P.H., Boom R.M. Nanofiltration of multi-component feeds. Interactions between neutral and charged components and their effect on retention. J. Membr. Sci. 2005;247:11–20. doi: 10.1016/j.memsci.2004.05.022. [DOI] [Google Scholar]
- 49.Escoda A., Fievet P., Lakard S., Szymczyk A., Déon S. Influence of salts on the rejection of polyethyleneglycol by an NF organic membrane: pore swelling and salting-out effects. J. Membr. Sci. 2010;347:174–182. doi: 10.1016/J.MEMSCI.2009.10.021. [DOI] [Google Scholar]
- 50.Shirley J., Mandale S., Williams P.M. Amino acid rejection behaviour as a function of concentration. Adv. Colloid Interface Sci. 2011;164:118–125. doi: 10.1016/J.CIS.2011.02.008. [DOI] [PubMed] [Google Scholar]
- 51.Kovacs Z., Samhaber W. Nanofiltration of concentrated amino acid solutions. Desalination. 2009;240:78–88. doi: 10.1016/j.desal.2007.11.067. [DOI] [Google Scholar]
- 52.Bargeman G., Westerink J.B., Guerra Miguez O., Wessling M. The effect of NaCl and glucose concentration on retentions for nanofiltration membranes processing concentrated solutions. Sep. Purif. Technol. 2014;134:46–57. doi: 10.1016/j.seppur.2014.07.025. [DOI] [Google Scholar]
- 53.Bandini S., Vezzani D. Nanofiltration modeling: the role of dielectric exclusion in membrane characterization. Chem. Eng. Sci. 2003;58:3303–3326. doi: 10.1016/S0009-2509(03)00212-4. [DOI] [Google Scholar]
- 54.Tonova K., Lazarova M., Dencheva-Zarkova M., Genova J. Nanofiltration of aquatic weed hydrolysate: diafiltration versus concentration mode for separating saccharides from phenolics. Chem. Eng. Res. Des. 2022;182:360–370. doi: 10.1016/J.CHERD.2022.04.011. [DOI] [Google Scholar]
- 55.Chandrapala J., Duke M.C., Gray S.R., Weeks M., Palmer M., Vasiljevic T. Nanofiltration and nanodiafiltration of acid whey as a function of pH and temperature. Sep. Purif. Technol. 2016;160:18–27. doi: 10.1016/J.SEPPUR.2015.12.046. [DOI] [Google Scholar]
- 56.Córdova A., Astudillo C., Santibañez L., Cassano A., Ruby-Figueroa R., Illanes A. Purification of galacto-oligosaccharides (GOS) by three-stage serial nanofiltration units under critical transmembrane pressure conditions. Chem. Eng. Res. Des. 2017;117:488–499. doi: 10.1016/J.CHERD.2016.11.006. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.