Fig. 4.

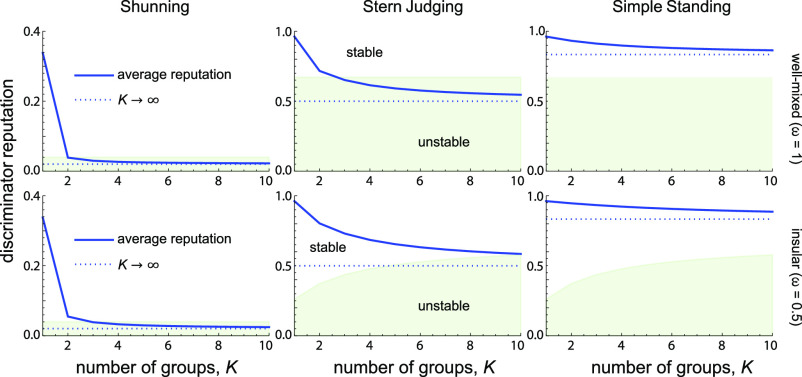
The average reputation in a population of discriminators, g|_{f^Z = 1}, depends on the number K of equally sized gossip groups (solid blue lines). Social interactions are either well mixed (ω = 1, top row) or they are biased toward in-group partners (ω = 0.5, bottom row). The shaded green region indicates the regime in which discriminators are susceptible to invasion by rare defectors; above this area, discriminators are stable against invasion, so that cooperative behavior is maintained. Increasing the number of gossip groups, K, rapidly reduces the average reputation in the population, to levels that can destabilize cooperation under Shunning or Stern Judging, whereas Simple Standing supports stable cooperation for arbitrarily many groups K. Insular social interactions (e.g., ω = 0.5 shown in the bottom row) tend to increase the average reputation while also reducing the threshold reputation required to stabilize discriminators against defectors. As a result, in the example shown for Stern Judging, the maximal number of gossip groups that support stable cooperation is greater when interactions are partly insular compared to well mixed. The dashed blue line indicates the asymptotic value of g^Z in the limit of many groups, K → ∞, which is equivalent to a model with private assessment (39). In all panels, b = 2, c = 1, and u_a = u_x = 0.02.