Missing portion sizes in FFQ – alternatives to use of standard portions

Abstract

Objective

Standard portions or substitution of missing portion sizes with medians may generate bias when quantifying the dietary intake from FFQ. The present study compared four different methods to include portion sizes in FFQ.

Design

We evaluated three stochastic methods for imputation of portion sizes based on information about anthropometry, sex, physical activity and age. Energy intakes computed with standard portion sizes, defined as sex-specific medians (median), or with portion sizes estimated with multinomial logistic regression (MLR), ‘comparable categories’ (Coca) or k-nearest neighbours (KNN) were compared with a reference based on self-reported portion sizes (quantified by a photographic food atlas embedded in the FFQ).

Setting

The Danish Health Examination Survey 2007–2008.

Subjects

The study included 3728 adults with complete portion size data.

Results

Compared with the reference, the root-mean-square errors of the mean daily total energy intake (in kJ) computed with portion sizes estimated by the four methods were (men; women): median (1118; 1061), MLR (1060; 1051), Coca (1230; 1146), KNN (1281; 1181). The equivalent biases (mean error) were (in kJ): median (579; 469), MLR (248; 178), Coca (234; 188), KNN (−340; 218).

Conclusions

The methods MLR and Coca provided the best agreement with the reference. The stochastic methods allowed for estimation of meaningful portion sizes by conditioning on information about physiology and they were suitable for multiple imputation. We propose to use MLR or Coca to substitute missing portion size values or when portion sizes needs to be included in FFQ without portion size data.

FFQ are commonly used in large-scale nutritional epidemiology studies, but some FFQ do not have questions about portion sizes^{( 1 – 3 )}. Details concerning portion sizes or missing portion size values are rarely accounted for in scientific publications, but when calculating the dietary intake from an FFQ, standard portion sizes are often applied.

The absence of portion size questions in an FFQ can be regarded as a missing data problem. Using standard portion sizes is methodologically equivalent to applying median portion sizes for all subjects. These may be sex-specific, but the size of portions depends on several other factors than sex such as age, BMI and physical activity^{( 4 )}. Hence, the standard portion size used may well be the same for a young physically active man as it is for an elderly sedentary man.

Substituting unknown portion sizes with standard sizes may thus under- or overestimate the ‘true’ intake in certain segments of the population^{( 5 – 7 )}. It is now well recognized that missing data are most rationally accounted for through multiple imputation techniques, rather than with deterministic imputations like medians, to avoid flawed (too narrow) confidence intervals^{( 8 , 9 )}. Multiple imputation requires an adequate method for imputation, i.e. a method with error and bias as low as possible.

In the present paper we describe how physiologically meaningful portion sizes can be estimated from information on age, sex, physical activity, weight and height by imputation from participants with complete data or from another FFQ data set with portion sizes (from a comparable population). We invented the ‘comparable categories’ method (Coca) and improved the ‘k-nearest neighbours’ (KNN) and the multinomial regression (MLR) methods by making them suitable for multiple imputation. The basic idea of these advanced imputation methods is that instead of using a median value for substituting missing data, one may condition on other information available in the data set to better estimate a reasonable portion size.

In the present study the dietary intake computed with standard portion sizes (the sex-specific median values), or with portion sizes determined by the MLR, Coca or KNN method, was compared with a reference dietary intake, which was computed with the originally self-reported portion sizes that were quantified by a photographic food atlas embedded in the FFQ.

Experimental methods

The Danish Health Examination Survey collected dietary data from 18 065 adult Danes in 2007–2008 using an Internet-based, 267-item FFQ^{( 10 )}. This diet inventory has been used in many Danish population studies^{( 2 , 11 )}. In the Danish Health Examination Survey, the FFQ was extended with a photographic food atlas consisting of eleven picture series placed at the end of the questionnaire in order to quantify the portion sizes^{( 11 )}. The portion size food atlas was developed by the Danish Veterinary and Food Administration. The picture series covered thirty-nine items (foods or meals) classified into four or six portions of varying sizes. For instance, six photos showed increasing serving sizes of corn flakes in a bowl and the accompanying portion size item was used to quantify all cereal frequency items (muesli, etc.). Another series with six photos of increasing serving sizes of a meat main meal was accompanied by five portion size items covering hamburger steak, steak, beef, fish or poultry. The remaining series of photographs covered bread, toppings for rye bread (eight items), toppings for white bread (eight items), warm stew with meat (three items), potatoes (four items), pasta, rice, vegetable dishes (four items), mixed salad, chocolate and candy. The actual weight in grams of the food on the picture was multiplied with the frequency to obtain the total intake of the food. Leisure-time physical activity was self-reported with the International Physical Activity Questionnaire in four classes, where class 1 was hard training multiple times per week and class 4 was inactive behaviour^{( 12 )}. We defined classes 1+2 as active and classes 3+4 as sedentary. Anthropometric measures were obtained by clinical examination in 9384 subjects. The present study population consisted of the 3728 subjects with complete information on anthropometry and portion sizes (no missing values). The characteristics of the study participants are described in Table 1. The involved institutions’ review boards have approved the study proposal.

Table 1.

Characteristics of the subjects with complete portion size data, included in the present study, compared with the excluded subjects with incomplete portion size data, Danish Health Examination Survey 2007–2008

	Men			Women
	Included	Excluded	P for difference	Included	Excluded	P for difference
n	1546	2078		2182	3578
Sex (%)	41	37		59	63
Mean age (years)	50·0	52·8	<0·001	48·4	51·3	<0·001
Mean BMI (kg/m2)	26·1	25·9	0·12	24·9	24·5	<0·01
Physical activity, % active	41	36	<0·01	25	25	0·61

Statistical methods

We analysed four methods of imputing portion size. The subjects were randomly divided (SAS procedure: proc surveyselect) into two data sets: (i) a learning data set A (n 1864) for generating data for imputation; and (ii) a test data set B (n 1864) for analysing the validity of the imputed data. For data set B the ‘mean daily total energy intake’ (TE) was computed with the complete set of authentic self-reported portion sizes and this TE served as the reference.

The population sex-specific medians were used as standard portion sizes. With each of the three stochastic imputation methods, we imputed portion sizes from data set A to data set B and used these estimated portion sizes to compute a new TE. This was done ten times (on different splits of the data) and subsequently ten TE values were computed with each imputation method.

The mean TE from each imputation method was then compared with the reference TE by determining the bias (defined as the mean error) and the root-mean-square error (RMSE). In the present paper the ‘error’ is defined as the reference value minus the estimated value. Spearman’s ρ was used to compare the ranking of the subjects, comparing the reference TE with the TE calculated with imputed portion sizes. T statistics were used to determine the bias in TE related to TE (Fig. 1). Energy and nutrient intakes were computed with FoodCalc^{® ( 13 )} and the Danish national food composition tables^{( 14 )}.

Fig. 1.

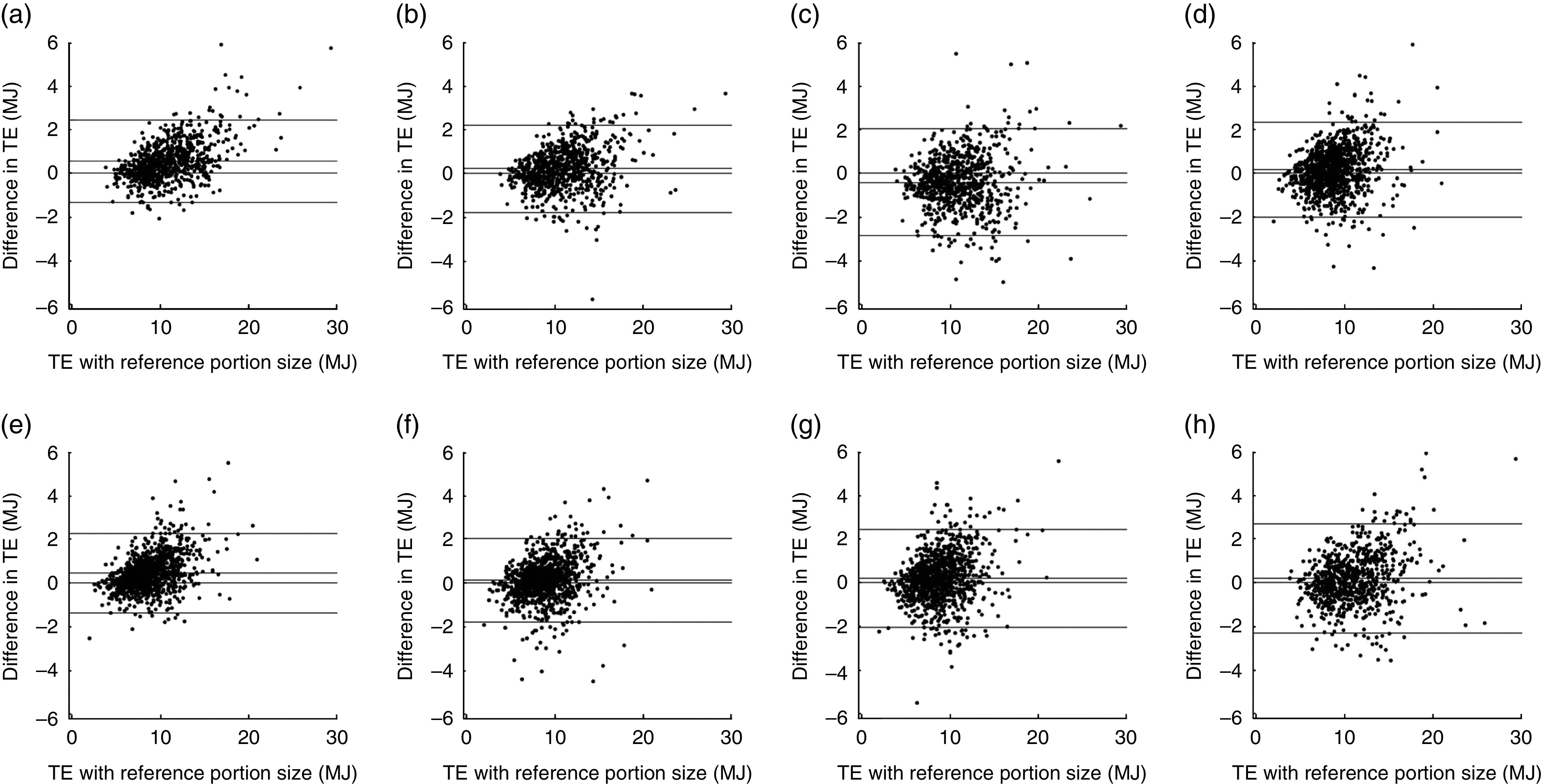
Total energy intake (TE) computed with the reference portion sizes (x-axis) is plotted against the difference between the reference TE and the TE computed with the portion sizes from each imputation method (y-axis): (a) median imputation in men (B=0·15, se=0·008, T=17·7); (b) MLR imputation in men (B=0·10, se=0·010, T=9·5); (c) KNN imputation in men (B=0·04, se =0·013, T=2·7); (d) Coca imputation in men (B=0·11, se=0·013, T=8·5); (e) median imputation in women (B=0·16, se=0·010, T=17·1); (f) MLR imputation in women (B=0·11, se=0.011, T=10·5); (g) KNN imputation in women (B=0·12, se=0·013, T=9·4); (h) Coca imputation in women (B=0·11, se=0·012, T=8·8). In this variation of a Bland–Altman plot, the x-axis denotes the reference value (and not the mean) as the error pertains solely to the imputed measure. The horizontal lines denote zero, the mean difference, +2 sd and −2 sd. B=the slope of a regression line: y=Bx+c. T=B/se; thus T denotes the tendency to underestimate portion sizes in subjects with high TE (and the reverse). High values of T denote stronger tendencies; the significance is implicit as T>1·95 implies P<0·05. Note: a positive value on the y-axis indicates an underestimation of the reference energy intake (imputation method: median, standard portion sizes, defined as sex-specific medians; MLR, multinomial logistic regression; KNN, k-nearest neighbours; Coca, ‘comparable categories’)

The four imputation methods were:

• 1.The ‘median’ method or ‘standard portion sizes’. Imputation of median values is equivalent to applying a standard portion size as it implies uniform portion sizes for all subjects (here thirty-nine medians, one for each of the thirty-nine portion size items). In this model we used the sex-specific median values from the entire sample (from data sets A+B) to define thirty-nine sex-specific standard portion sizes in data set B (using the sex-specific median from data set A only would induce bias as explained in the online supplementary material, chapter 4). Based on earlier reports and physiological reasoning we hypothesized that portion sizes depend on age, sex, physical activity, weight and height^{( 4 , 6 )}. Individual data on these five variables are readily available in most epidemiological studies and they informed the following three, more advanced imputation methods that are all based on stochastic principles:
• 2.The ‘comparable categories’ (Coca) method. The subjects were divided into thirty-two categories. Supplemental Table S1 in the online supplementary material demonstrates how the categories were created by first dividing the subjects by level of physical activity (into active or sedentary), then dichotomized on approximate median values of height (166 cm), then divided by sex, split on rough median values of weight (74 kg) and age (48 years). Each of these categories contains individuals sharing approximately the same physiological characteristics, e.g. in category 13 everyone was sedentary, >166 cm, female, <74 kg and <48 years. For each subject in data set B, the portion sizes were substituted by a complete set of portion sizes from one random subject in the ‘comparable category’ in data set A.
• 3.The ‘k-nearest neighbours’ (KNN) method^{( 15 )}. A missing portion size in data set B was substituted by a random value from the k (a predefined number) most similar observations (‘neighbours’) in data set A. The similarity is defined as the proximity measured by Euclidean distance between the informing variables (here age, sex, physical activity, weight and height). While traditional KNN would impute the portion size most prevalent among the k neighbours, our version of KNN imputed a random value among the k neighbours with probability proportional to the proximity, making it suitable for multiple imputation. k>20 yielded no extra accuracy.
• 4.The ‘multinomial logistic regression’ (MLR) method. MRL models were constructed based on data set A: age, weight and height were continuous covariates, sex and physical activity were categorical covariates, and the portion sizes were the categorical outcomes. Portion sizes in data set B were determined by probability sampling from the prevalence of the categorical portion size values obtained by inserting the data set B values for age, weight, height, sex and level of physical activity in the regression model.

The set-up was run in the SAS statistical software package version 9·2, but the methods can be applied on any type of software. SAS codes for KNN, MLR, Coca and a wrapper for (linear) regression analysis combining the results from multiple imputed (by any method) data sets are given in the online supplementary material.

Results

More women than men participated in the Danish Health Examination Survey. The subjects included in the present study were a little younger than the excluded subjects. Furthermore, the included men were more active and the included women were slightly heavier. However, differences were numerically small (Table 1).

Overall, compared with the reference energy intakes, the RMSE were equally low with the median and MLR methods, and equally high with Coca and KNN. The bias of the median method was numerically larger than in any of the other methods (Table 2). KNN had a negative bias in men (overestimating the portion sizes), but a positive bias in women (underestimating the portion sizes). The biases of MLR and Coca were equally low in both men and women.

Table 2.

Mean daily energy intake among 3728 adults with complete portion size data (reference), compared with energy intakes calculated with portion sizes derived from four imputation methods, Danish Health Examination Survey 2007–2008

	Men							Women
	Energy		95 % CI	RMSE	95 % CI	Bias	95 % CI	Energy		95 % CI	RMSE	95 % CI	Bias	95 % CI
	%	MJ	MJ	kJ	kJ	kJ	kJ	%	MJ	MJ	kJ	kJ	kJ	kJ
Total energy
Reference	–	10·97	10·81, 11·13	Ref.	–	Ref.	–	–	8·81	8·69, 8·92	Ref.	–	Ref.	–
Median	–	10·45	10·37, 10·50	1118	1098, 1139	579	563, 596	–	8·28	8·26, 8·30	1061	1011, 1111	469	455, 482
KNN	–	11·37	11·32, 11·41	1281	1262, 1299	−340	−365, −315	–	8·53	8·51, 8·56	1181	1129, 1234	218	191, 244
MLR	–	10·78	10·73, 10·83	1060	1028, 1092	248	223, 274	–	8·57	8·55, 8·60	1051	997, 1105	178	161, 195
Coca	–	10·80	10·75, 10·83	1230	1196, 1264	234	207, 261	–	8·56	8·54, 8·59	1146	1087, 1205	188	166, 210
Fat
Reference	31·2	3·43	3·36, 3·49	Ref.	–	Ref.	–	29·9	2·64	2·60, 2·68	Ref.	–	Ref.	–
Median	31·8	3·32	3·31, 3·34	375	364, 386	124	119, 130	30·8	2·55	2·54, 2·56	305	292, 317	67	65, 70
KNN	31·7	3·61	3·59, 3·63	502	491, 513	−161	−175, −146	30·0	2·56	2·56, 2·57	395	387, 404	56	47, 64
MLR	31·2	3·37	3·36, 3·39	392	381, 403	75	68, 82	30·0	2·57	2·56, 2·58	345	330, 361	45	39, 51
Coca	31·3	3·38	3·36, 3·39	473	458, 489	70	59, 81	30·0	2·57	2·56, 2·58	392	377, 407	49	43, 54
Protein
Reference	16·1	1·77	1·74, 1·80	Ref.	–	Ref.	–	16·3	1·44	1·42, 1·45	Ref.	–	Ref.	–
Median	16·5	1·72	1·71, 1·73	210	205, 215	57	54, 60	16·7	1·38	1·38, 1·38	191	188, 193	49	47, 50
KNN	16·3	1·86	1·84, 1·87	273	267, 279	−78	−87, −69	16·1	1·38	1·37, 1·38	251	246, 257	53	48, 58
MLR	16·2	1·74	1·73, 1·75	220	214, 225	37	32, 42	16·4	1·41	1·40, 1·41	211	205, 216	21	18, 25
Coca	16·2	1·75	1·73, 1·76	271	263, 278	34	27, 40	16·4	1·41	1·40, 1·41	249	243, 256	23	20, 26
Carbohydrates
Reference	42·2	4·63	4·57, 4·68	Ref.	–	Ref.	–	44·0	3·88	3·83, 3·92	Ref.	–	Ref.	–
Median	41·0	4·28	4·26, 4·30	613	598, 627	362	354, 371	42·7	3·54	3·52, 3·55	675	616, 733	319	307, 330
KNN	41·6	4·73	4·71, 4·76	672	656, 688	−92	−111, −73	44·1	3·77	3·75, 3·78	693	636, 750	88	70, 105
MLR	41·9	4·52	4·49, 4·55	580	560, 599	122	106, 138	43·8	3·75	3·77, 3·77	640	576, 704	100	86, 114
Coca	41·9	4·53	4·50, 4·55	602	585, 621	116	104, 128	43·8	3·75	3·73, 3·77	652	595, 708	105	89, 121

RMSE, root-mean-square error; bias, mean error; median, sex-specific median imputation which is equivalent to using sex-specific standard portion sizes; Coca, ‘comparable categories’; KNN, k-nearest neighbours; MLR, multinomial logistic regression; Ref., referent category.

The four methods were compared by their ability to predict the reference. The reference energy intakes were computed with a set of complete reported portion sizes. The results presented are mean values of ten imputations with each method (on random splits of the data). Note that a positive bias indicates an underestimation of the reference and a negative bias indicates an overestimation.

More results are presented in the online supplementary material (Supplemental Table S2), including ‘non sex-specific’ standard portion sizes and different versions of Coca (with different informing variables and less categories). Results with selected micronutrients and macronutrient subtypes were essentially similar to the analyses of macronutrients (results not shown).

All of the methods had high Spearman’s rank correlation, but median and MLR imputation performed slightly better than KNN and Coca. All correlations were >0·90 and all confidence intervals between 0·89 and 0·97 (see online supplementary material, Supplemental Table S3).

Figure 1 illustrates how all methods resulted in a bias of TE dependent on TE, i.e. an underestimation of TE in subjects with a high energy intake and an overestimation of TE in subjects with a low energy intake. The magnitude of this bias (the T value) was markedly higher with median imputation than with the other methods. Figure 2 shows that when stratifying by BMI group, age group and physical activity class, a larger variation was seen among men than women regarding the accuracy of the imputation methods. The mean total energy intake was 12·5 MJ calculated with maximum portion sizes for all and 7·5 MJ with minimum portion sizes for all. Thus, up to 40 % of the calculated energy intake was potentially determined by the portion sizes. However, Fig. 2 indicates that the mean energy intakes calculated differed by up to 2 MJ (18 %) in men between the methods and by to 0·75 MJ (9 %) in women.

Fig. 2.

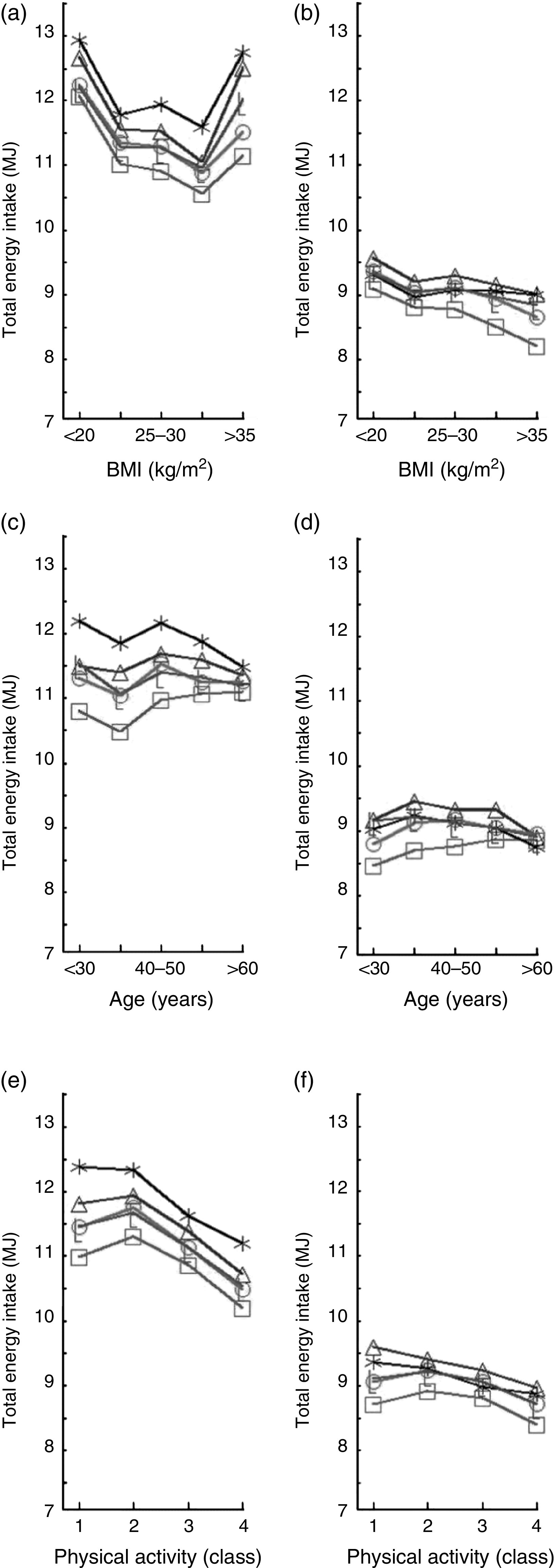
Mean daily total energy intake is plotted against BMI (a, b), age (c, d) and level of physical activity (e, f), separately for men (a, c, e) and women (b, d, f). The reference (——) is computed with the originally reported portion sizes. The total energy intake has been computed with portion sizes determined by four different imputation methods: —□—, median (equivalent to sex-specific standard portions); —L—, MLR (multinomial logistic regression); —○—, Coca (‘comparable categories’); ——, KNN (k-nearest neighbours). The results presented are mean values of ten imputations with each method (on random splits of the data)

Discussion

Overall, the MLR method provided the best agreement with the reference dietary intake. However, the differences between the stochastic methods were small and the confidence intervals of the bias in MLR and Coca were overlapping in most segments of the data. In MLR and Coca the bias did not differ substantially between men and women, whereas in KNN the bias was negative in men and positive in women. The median method (equivalent to sex-specific standard portion sizes) had relatively low RMSE but was inferior to the other methods in terms of bias. All of the methods underestimated the reference dietary intake, except KNN that overestimated the portion sizes in men. The use of standard portion sizes systematically underestimated the energy intake of subjects with large portion sizes; a bias that diminished, for instance, differences in dietary intake between age groups. For example, a young man was assigned the same standard portion size as an elderly man even though we know that age is a determinant of energy intake as demonstrated in Fig. 2 and by the fact that age is an input variable in calculating the BMR^{( 16 )}. This bias may well affect parameter estimates in multivariate analyses^{( 17 )}. On the other hand, the median method performed better than the other methods in Spearman’s rank test. However, the confidence intervals were overlapping with MLR, and Coca and KNN also had high correlations with the reference energy intake.

Figure 2 demonstrates how all imputation methods were better in predicting portion sizes in women than in men. The greater variation in men is in part explained by the higher energy intake, but probably also by a greater variation in portion sizes in men.

Evaluation of the methods

We used ‘sex-specific median imputation’ as ‘standard portions’. Standard portions can of course be defined differently, but any deterministic portion size will contain the same sort of bias and the median sizes were probably a reasonable choice.

The simple Coca method worked surprisingly well and, compared with the other stochastic methods, the computer run time was much faster. Depending on the size of the learning data set and the number of categories, empty or tiny categories may occur. This can be solved by fitting cut-off values in the dichotomization or by merging related categories. The relatively basic categorization can probably be altered to improve performance. More considerations about the different versions of the methods are presented in the online supplementary material.

External validity

The variables physical activity, sex, age, height and weight informed the three multiple imputation methods. Consequently, the three models had access to the same information. We also tested the methods including resting heart rate and ‘number of potatoes with warm meals’. By including the latter, all of the methods performed slightly better, and by including heart beat rate all of the methods performed slightly worse, but the methods performed approximately equally. The present five informing variables were chosen as they are readily available in most data sets.

The external validity of the methods may be questioned as the included subjects differed slightly from the excluded. However, the question is not whether the included and the excluded were comparable, but rather whether the relationship between physiology and portion sizes was different among the included and excluded, which does not seem very plausible.

Our reference or ‘gold standard’ was calculated from self-reported FFQ data with varying portion sizes and did not take into account information bias. It is well documented how self-reported values only to some degree reflect true intakes and that reporting of specific macronutrients may be differentially biased according to sex, weight and BMI^{( 18 , 19 )}. All of the methods were affected by this reporting bias. Median and MLR are model-based and thereby the reporting error affected the model and had an overall effect on all imputations, i.e. possible over- and under-reporting will be spread out over the whole data. In contrast, Coca and KNN imputations are based on pairing similar individual observations and hence a systematic error will persist within the corresponding segments of the data.

Missing single values

Concerning FFQ with individual portion size questions, the MLR, Coca or KNN method can be used to substitute missing single values. In the Danish Health Examination Survey, from where the present data derive, 17·7 % of the questions on portion sizes were missing which is not uncommon in an FFQ^{( 20 )}. Currently, most studies probably ‘fill in the blanks’ with median values or standard portions^{( 21 )}. As demonstrated in the present study, median imputation generates bias. If only a few values are missing the resulting bias may be negligible, but the impact of median imputation bias increases with the number of missing values. If one of the stochastic methods is used for imputation of single missing values, a comparable data set is always at hand: the subset of data with no missing values. We have supplied Coca SAS codes for this use in the online supplementary material.

FFQ without portion sizes

MLR or Coca may be used to include portion sizes in FFQ without individual portion size questions. In this case the portion sizes will have to be imputed from a comparable data set with portion sizes. Often traditional FFQ have later been improved with portion size questions and if the populations are similar, data from newer semi-quantitative FFQ can be used as learning data set. We have supplied SAS codes for this use also in the online supplementary material.

Multiple imputation

When applying multiple imputation, the multivariate analyses are run on multiple (e.g. ten) data sets each with different imputed values. The resulting parameter estimates are then the mean values of the ten analyses^{( 7 )}. In the present paper we did not test our imputation methods’ ability to predict parameter estimates, but solely the ability to predict the reference TE, using ten imputations for each method. The online supplementary material provides SAS codes on how to do multiple regression modelling with multiple data sets.

In summary

MLR and Coca are both valuable methods for including portion sizes in FFQ or substituting missing portion size values. The KNN method seemed less attractive due to the differential bias in men and women, and the relatively high RMSE. In general, these three stochastic methods allowed for estimation of meaningful portion sizes by conditioning on information about physiology and they were suitable for multiple imputation. Application of sex-specific standard portion sizes inferred more bias than the other methods tested and diminished differences in energy intake related to age, for instance. We propose to use the MLR or Coca method to substitute missing portion size values or when portion sizes need to be included in FFQ without portion size data.