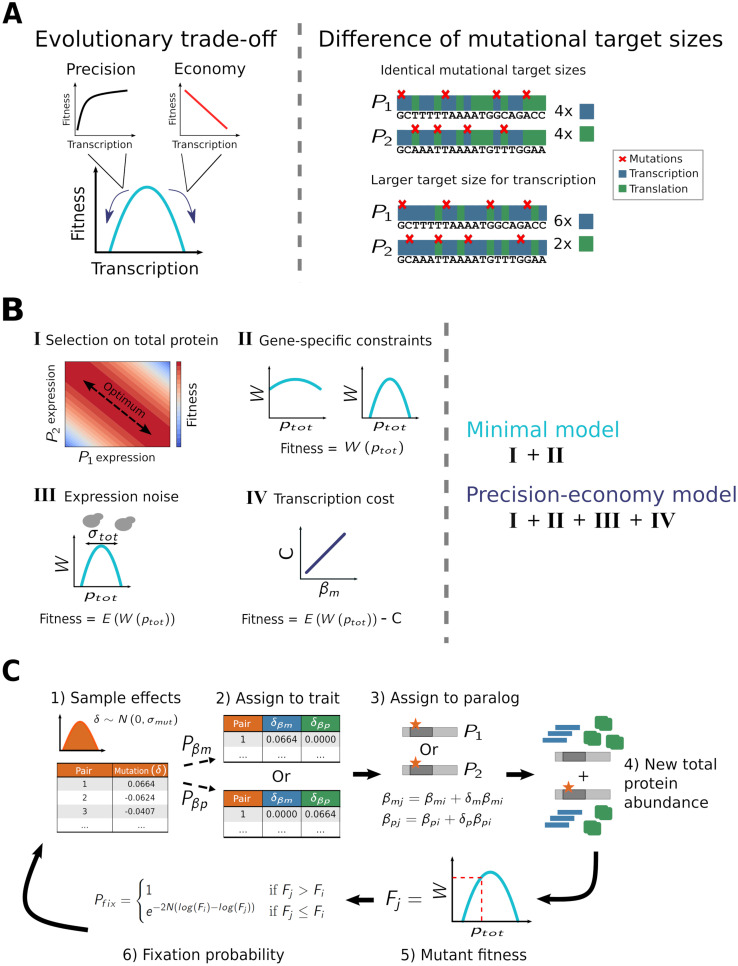
Fig 2. Overview of the modeling and simulation approach.

(A) Two hypotheses are considered: an evolutionary trade-off between the precision and economy of gene expression (left) and a larger mutational target size for transcription than for translation (right). (B) A minimal model of post-duplication evolution is defined under the assumption that selection acts to maintain the cumulative protein abundance of two paralogs. Parabolic functions of fitness according to cumulative protein abundance with varying curvatures are used for different gene pairs. The model is complexified by the addition of precision-economy constraints [25] to test the hypothesized evolutionary trade-off. (C) The expression divergence of paralogs is simulated by sequential fixation, through multiple rounds of mutation-selection. A relative mutational effect δ is first sampled from a normal distribution of mean 0 and standard deviation σ_mut for each paralog pair. It is then assigned to transcription or translation rate, according to relative probabilities P_βm and P_βp. This mutation is randomly performed on one of the two paralogs P₁ and P₂, which are equally likely to be mutated. The transcriptional (δ_βm) or translational (δ_βp) mutational effect is applied in such a way that it increases or decreases expression by a fraction of its current level. A new mutant fitness F_j is obtained from the resulting cumulative protein abundance and/or transcription rates, according to the minimal model or its precision-economy version. By comparing this fitness to its ancestral value F_i, a fixation probability is computed [34], according to which the mutation is instantly fixed or lost at random. The mutation-selection process is repeated until a realistic level of protein abundance divergence is reached (Methods).