Extended Data Fig. 8 |. M2 does not represent arbitrary sequences.

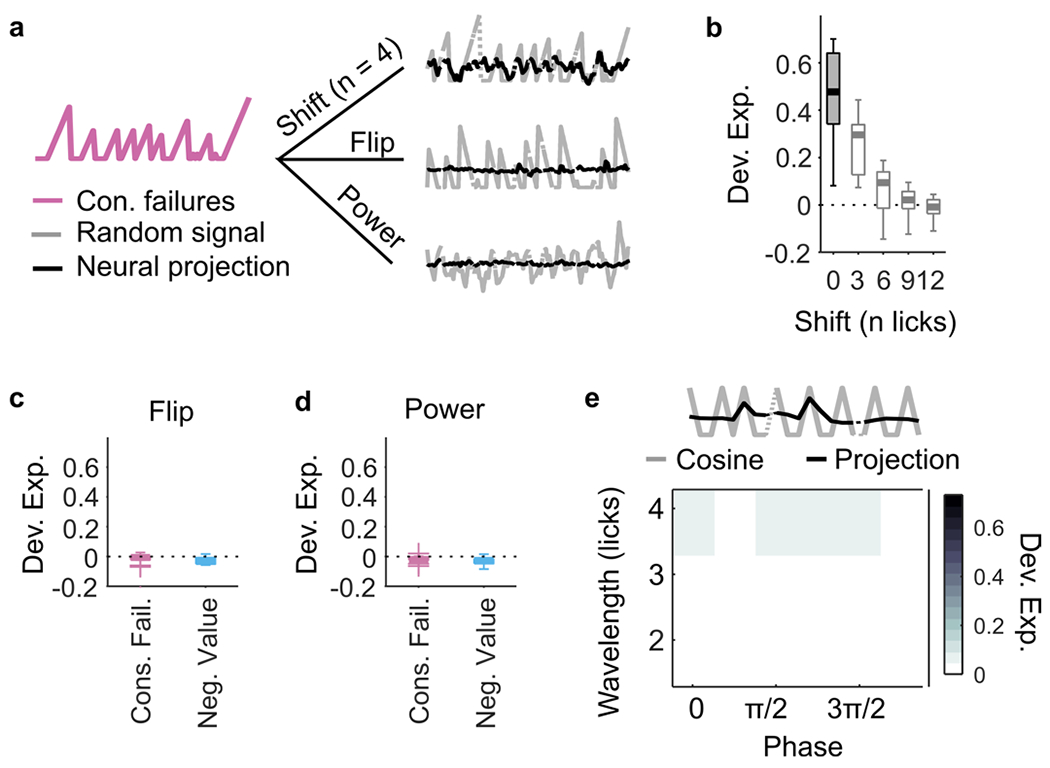
(a) A ‘near universal’ representational capacity is a feature of a computational framework known as ‘reservoir computing’ that exploits a potential functional capacity of recurrent networks to represent combinations of current inputs with previous evidence, even arbitrary ones. Thus, to test whether M2 also represented arbitrary signals, we examined whether sequences with similar temporal structure as the DVs but with no obvious relevance to the task could be decoded from M2. Here are examples of random sequences (gray) generated from one of the DVs (pink, here consecutive failures). The DV can lead to a shifted version (top right), a flipped version (middle right) or a random signal with equal power spectra. Each random signal is then decoded from M2 population activity (black traces). (b) Deviance explained (ordinate) by M2 neurons from decoding the DVs shifted by a given number of licks (abscissa). On each box, the central mark indicates the median across recording sessions (n = 11 sessions), and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points. The dash black line indicates chance level (Dev. Exp. = 0). Shifting the DVs by a delay greater than their temporal autocorrelation greatly impaired their decodability (one-way ANOVA, F = 62.81, p < 10⁻²⁶). (c) Same as in (b) but for DVs flipped across sessions. None of the flipped signals were decodable from M2 population activity. (d) Same as in (c) but for random signals with power spectra that match each DV. None of the random signals were decodable from M2 population activity. (e) Since any signal can be approximated by sums of periodic functions (Fourier analysis), we also probed the capacity of M2 to represent arbitrary temporal sequences by testing whether we could decode from M2 a basis set of cosine functions with wavelengths in the dynamic range of what we observed with integration and reset of rewards (example top gray trace; wavelength = 4 licks, phase = 0 rad). Overall, the decoding quality of the periodic function (example neural projection, top trace in black, Dev. Exp. = −0.002) was close to chance level (Dev. Exp. = 0.024 ± 0.028, median ± MAD) as seen in the matrix of deviance explained from decoding sequences with different wavelengths and phases with M2 population activity.