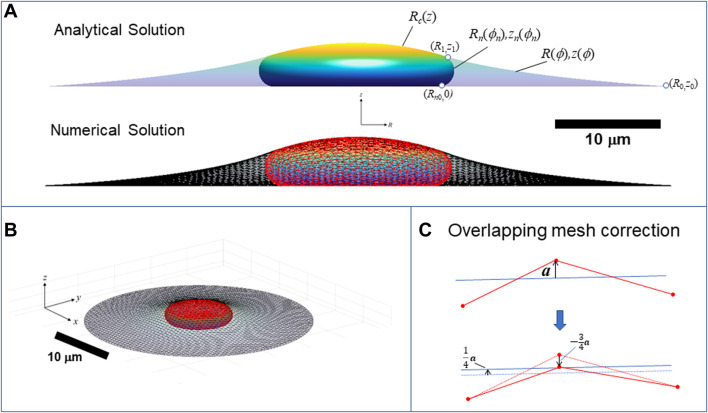
FIGURE 9.

Calculation of three-dimensional cell and nuclear shapes. (A) Analytical axisymmetric surfaces of constant mean curvature for the cortical surface interface with the surroundings, (R,z), nucleus-cytoplasm interface containing the nuclear lamina, (R _n ,z _n ), and joint nucleus-cortical interface with the surroundings, R _c (z). Surfaces are matched at point (R ₁,z ₁), and R _n is the radius to which the nucleus presses against the substratum. The calculation shown here is for V = 900 μm³, V _cell = 3.4V, ε = 0.45, and spread radius of R ₀ = 30 μm (z ₀ = 0), (B) 3D numerical calculation for the same conditions obtained minimizing the surface areas and simultaneously optimizing the triangular mesh by maintaining a centroidal Voronoi tessellation using the algorithm in (Pan et al., 2012). Nuclear and cortical surfaces were solved simultaneously for the for the given adhesion footprint under the constraints of constant nuclear surface area, nuclear volume, and cell volume. The method is validated by close agreement with the exact analytical solution for an axisymmetric spread cell. (B) Elevated perspective of the same 3D cell from (A). (C) Illustration of algorithm for preventing the crossing of meshes. When a vertex point (shown as red dot on projected triangle edges) crosses an opposing mesh triangle surface (indicated by blue line), with distance vector from the nearest triangle surface $\mathit{a}$ , the vertex is pushed back by distance $-\frac{3}{4}\mathit{a}$ , and each of the three vertices of the opposing triangle is pushed forward by $+\frac{1}{4}\mathit{a}$ . In this way, the vertex ends up on the plane of the triangle, and the forces balance on the two surfaces, with each vertex of the opposing triangle shares and equal share of the force.