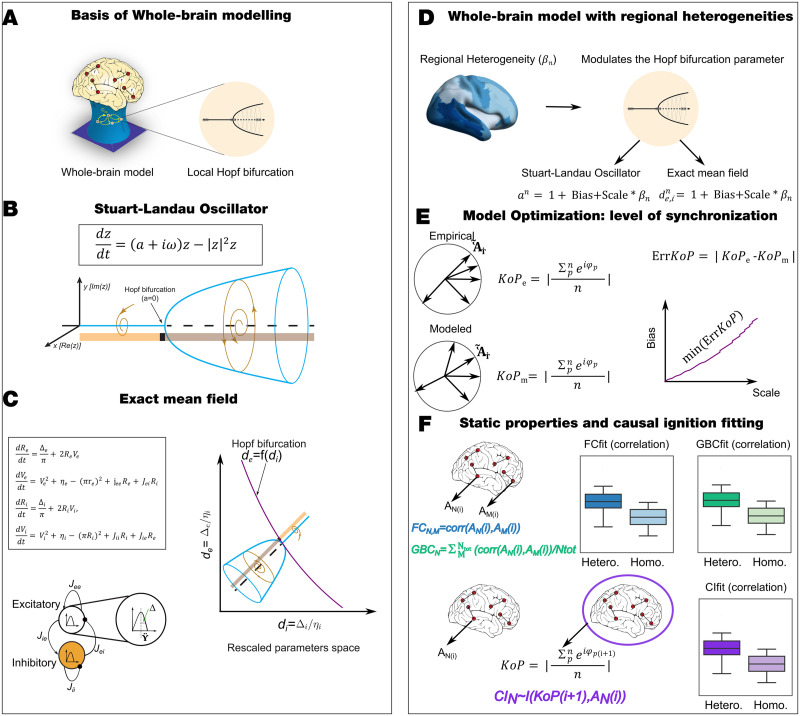
Figure 1. .
Overview of framework. (A) Whole-brain models integrate anatomy and local dynamics that in our work present a Hopf bifurcation, that is, the capability to change the dynamical behavior from a fixed point governed by noise toward sustained oscillations. These whole-brain models are able to reproduce static and dynamic properties computed from empirical fMRI data. (B) The Stuart–Landau equation is the simplest representation of a Hopf bifurcation and is suited for describing the transitions between noise and oscillation by varying only one bifurcation parameter, a. (C) The exact mean-field model is derived from neuronal quadratic integrate-and-fire equations in the thermodynamic limit (i.e., large number of neurons). The resulting firing rate equations (FRE) describe the dynamics of the mean firing rate (R) and the mean membrane potential (V) of a heterogeneous population of all-to-all coupled neurons. The heterogeneity within each population of neurons lies in the input current that each neuron received and is described by a Lorentzian distribution of half-width Δ and center η. The generalization of a pool of interacting inhibitory and excitatory populations includes an equation for the mean firing rate and mean membrane potential for each population and a coupling term modulated by the mean synaptic strength factor, J. We reduced the number of parameters of the system by the nondimensionalization of FRE equations rescaling and redefining the variables and parameters. The dynamical landscape of an interacting population of inhibitory and excitatory neurons presents a Hopf bifurcation in two-dimensional phase diagram determined by the rescaled half-width of the Lorentzian distribution de− = Δe/ηi − di− = Δi/ηi, which are named bifurcation parameters, with other model parameters fixed (η = ; jee = ; jie = ; jie = jii = −). (D) The regional heterogeneity modulates the bifurcation parameter, a, in the Hopf whole-brain model, and the parameters de and di in the exact mean-field whole-brain model. The modulation consists of an additive term, named the bias, and a term that is a factor multiplying the regional heterogeneity, called scale. (E) We fit the homogeneous model to the empirical level of synchronization measures as the mean of the modulus of the Kuramoto order parameter (KoP) computed by the absolute difference between the empirical and the modeled values (ErrKoP). The bias and scale are explored and a curve of the minimum level of ErrKoP is determined. (F) We compute the model fit capacity to other static and dynamic properties along the curve of iso-level of minimum ErrKoP. We find that for all the measures, the heterogeneous model outperforms the homogeneous model.