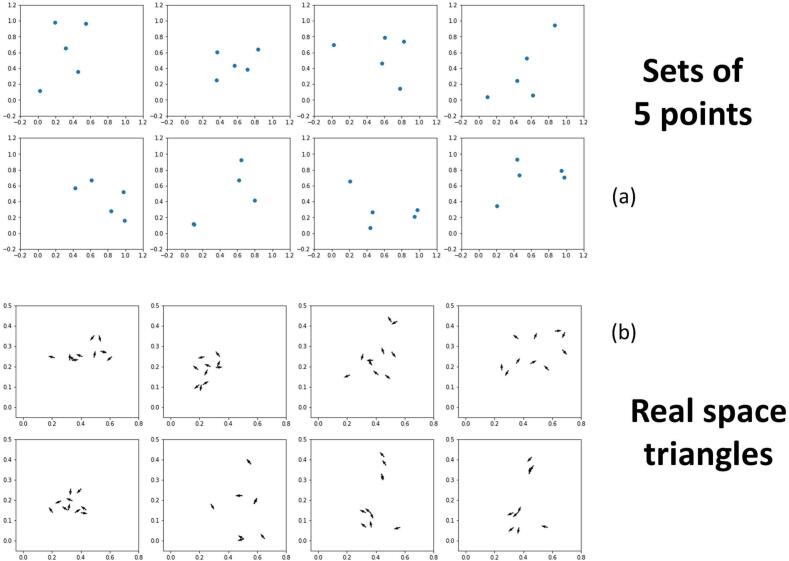
Fig. 4.

Examples of patterns compact in (a) real space (5 points) and their (b) third order invariants as given by Eq. (4.8). The real space invariants are expressed by writing down for each of the 10 triangles formed by the 5 points, the 1. short side, 2. the drop (as discussed in Fig. 3 and the angle between these two vectors. Short side and drop are given by the two axes shown, whereas the angle is represented by the direction of the arrow on top of the point. Each pattern of invariants are very different except for the pattern of invariants of the last two of the (b) subpanel. The original real space set of points are shown in the last two plots of panel (a); these patterns are clearly seen to be mirrors. In the invariants, this corresponds to mirroring the vectors across the x-axis.