Fig. C1.

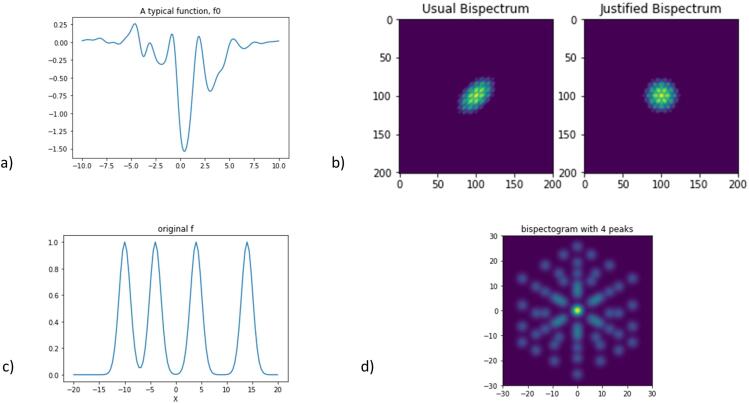
1D bispectrum: Many of the coordinate transformations developed in this manuscript, apply to the 1D bispectrum as well. In a) is a simple nicely windowed and smooth signal. The bispectrum, in frequency space, usually appears (Chua et al., 2008) in the literature as an ellipsoid as in the left side of b). However, with the similar type of coordinate changes introduced here, a 3–2 symmetry emerges, which corresponds to the 6 orderings in size that the lengths of a triangle may have. We call this the justified pattern (in Fourier space) which appears in the right side of b). In c) is drawn a highly punctate 1D signal with 4 peaks. The justified bispectrum is created and inverse Fourier transform can be taken as described in Section 4. Along the 3–2 symmetry lines lie the “skinny triangles” arising from the interference of the same peak twice, whereas the bright spot in the center corresponds to the triple correlations of single peaks. Triangles corresponding to three different peaks lie in the wedge between the 3–2 symmetry lines. Four peaks can form a total of 4 different true triple correlations (combinatorially, this is 4 choose 3). These 4 peaks are shown clearly in the wedges. One can infer the relative positions of the peaks, by the placement of the 4 peaks in the real space wedge. The situation for rabs in arbitrary dimension has all this same facets: i) symmetry hyperplanes corresponding to self terms, and ii) a 6-fold symmetry from which one should choose an asymmetric unit.