FIGURE 1.

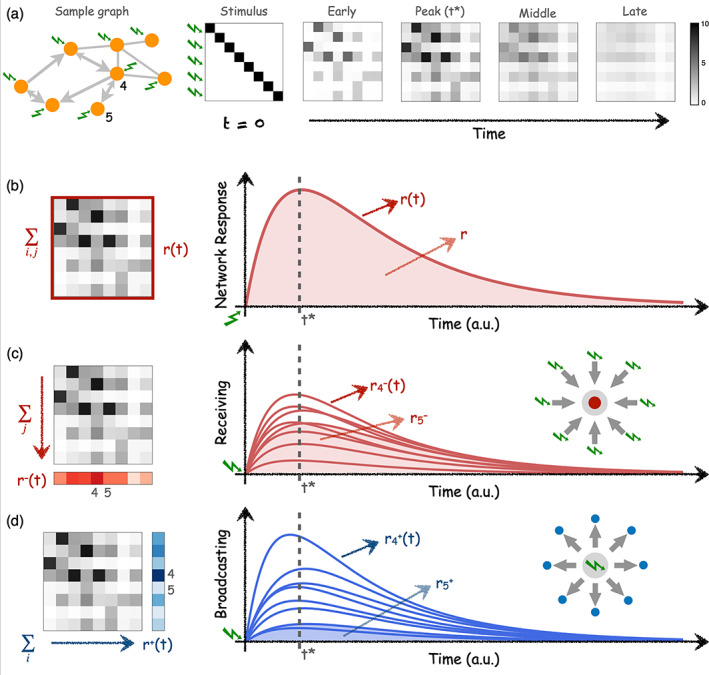
Network analysis via simulation of perturbation‐responses. (a) Temporal evolution of pair‐wise responses to an initial unit perturbations at time $t=0$ applied at every node of a sample network. The network is directed and weighted, thus pair‐wise responses are asymmetrical. The subsequent analysis of responses can be performed at different levels. (b) The global network response $r\left(t\right)$ is computed as the sum of all pair‐wise responses at each time t. Global network response rapidly peaks at time t* and slowly decays as a consequence of the leakage term in Equation (2) resembling a dissipation of signal at the brain regions. $r$ is thus the total accumulated response in the network and is calculated as the integral (area‐under‐the‐curve) of $r\left(t\right)$. (c) The ‘Receiving’ capacity $r_i^{-}\left(t\right)$ is the temporal response of one node to all the inputs applied at $t=0$. It is thus a signature of how much of the network flows centralise at a given node, which is a (necessary but not sufficient) condition of a node to integrate information. $r_i^{-}\left(t\right)$ is calculated as the column‐sum of the response matrices $R\left(t\right)$. (d) The ‘Broadcasting’ capacity $r_i^{+}\left(t\right)$ the nodes represent the influence that node i exerts over the network by quantifying the amount of response elicited over all the nodes by an input applied at node i. Thus, $r_i^{+}\left(t\right)$ is calculated as the row‐sum of the response matrices $R\left(t\right)$. For illustration, the behaviour of two nodes, $i=4$ and $i=5$ are highlighted. Node 4 is a central and node 5 is a ‘leaf’ only connected to node 4. As a consequence, node 4 has the largest receiving and broadcasting capacities in the network. A strong connection 4 → 5 implies that node 5 is very much influenced by the network (large receiving) but a weak connection 5 → 4 results in that node 5 can barely influence the other nodes (low broadcasting).