Probabilistic estimation for across‐batch compatibility enhancement for amyloid PET

Abstract

INTRODUCTION

It is necessary to accurately account for systematic differences due to variability in scanners, radiotracers, and acquisition protocols in multisite studies combining amyloid imaging data.

METHODS

We propose Probabilistic Estimation for Across‐batch Compatibility Enhancement (PEACE), a fully Bayesian multimodal extension of the widely used ComBat harmonization model, and we apply it to harmonize regional amyloid positron emission tomography data from two scanners.

RESULTS

Simulations show that PEACE recovers true harmonized values better than ComBat, even for unimodal data. PEACE harmonization of multiscanner regional amyloid imaging data yields results that agree better with longitudinal data compared to ComBat, without removing the known biological effects of age or apolipoprotein E genotype.

DISCUSSION

PEACE outperforms ComBat in both unimodal and bimodal contexts, is applicable to multisite amyloid imaging data, and holds promise for the harmonization of other neuroimaging data over ComBat.

HIGHLIGHTS

• We introduce PEACE, a fully Bayesian multimodal extension of ComBat harmonization.

• Simulations show that PEACE recovers true harmonized values better than ComBat.

• PEACE accurately harmonizes multiscanner regional amyloid imaging data.

1. INTRODUCTION

Amyloid‐β positron emission tomography (PET) allows for the assessment of an early neuropathological hallmark of Alzheimer's disease (AD). ¹ Multisite studies combining amyloid PET data from different scanners, radiotracers, and acquisition protocols are becoming more common to enable the examination of research questions where effect sizes may be small. Combining data across sites requires accounting for systematic differences in amyloid measurements.

Several approaches have been proposed for harmonizing amyloid PET data. They can be grouped into three categories based on the type of measurement being harmonized: reconstructed PET image, parametric image, or regional or global statistics of the parametric image. An approach in the first category is to apply spatial smoothing to the reconstructed PET image to achieve a common resolution across sites. ² Examples in the second category for harmonizing standardized uptake value ratio (SUVR) images include approaches based on non‐negative matrix factorization (NMF) ³ and deep learning. ⁴ Both of these approaches have been trained using cross‐over data (i.e., data for same participants scanned with multiple radiotracers, scanners, or acquisition protocols), though the models can be applied without requiring cross‐over data if an applicable trained model is available. Examples in the last category include Centiloids ⁵ and Nonlinear Distributional Mapping (NoDiM). ⁶ Centiloids were developed to calibrate global amyloid measurements from various sites and radiotracers against a common reference scale. The function for converting amyloid PET measurements to Centiloids is an affine transformation that yields a mean of 0 within a control group aged ⩽ 45 and a mean of 100 within a group of AD patients. When such groups are not available, an approximate transformation can be determined by applying one's image processing pipeline to the GAAIN Centiloid dataset for the radiotracer of interest (https://www.gaain.org/centiloid‐project) and finding the transformation using the results of this processing. However, this approximate procedure does not account for inherent differences due to scanners or acquisition protocols. Recent work has focused on using parametric image‐based harmonization, such as the NFM‐based method, in conjunction with Centiloid calibration, to further minimize site differences. ³ , ⁷ NoDiM is similar to histogram matching but uses the estimated cumulative density functions based on a two‐class Gaussian mixture model (GMM) for aligning the distributions of global amyloid measurements across sites. ⁶ While NoDiM improves upon Centiloids, it assumes that the proportion of individuals with elevated amyloid in each site is the same.

ComBat is a harmonization approach originally developed for gene array data ⁸ and has since been applied with modifications and improvements to magnetic resonance imaging (MRI) data, ⁹ , ¹⁰ , ¹¹ , ¹² including voxelwise and regional measurements. It has been extended to handle longitudinal measurements ¹³ and non‐linear relationships. ¹⁴ ComBat has also been applied to fluorodeoxyglucose PET, ¹⁵ , ¹⁶ but its utility has not been demonstrated for amyloid PET. ComBat assumes a unimodal distribution of measurements conditional on covariates. This assumption is violated in the case of amyloid imaging data, which exhibit a bimodal distribution. ¹⁷ The unimodality assumption was relaxed in GMM‐ComBat, ¹² where a two‐class GMM is fitted to each feature separately and the model with the best fit is used to assign each scan to one of the two clusters. The cluster assignment is then used as a batch effect in ComBat, followed by another application of ComBat to account for site effects separately within each cluster. This method seeks to remove cluster differences. In the context of amyloid PET imaging, this amounts to removing differences between low and high amyloid burden groups and, therefore, is not suitable.

In this paper, we propose an approach to harmonizing regional amyloid PET measurements across different sites that does not require data from specific subgroups or cross‐over data and does not make the assumption that the proportion of individuals with elevated amyloid is the same across sites. Our approach, Probabilistic Estimation for Across‐batch Compatibility Enhancement (PEACE), makes two substantial changes to ComBat. First, we incorporate a GMM informed by all input features simultaneously, integrating cluster assignment within harmonization. Second, instead of empirical Bayes, we employ a fully Bayesian approach, enabling the computation of uncertainty around harmonized values. Using simulations, we demonstrate that PEACE yields harmonized values that agree better with true values compared to ComBat. We then apply PEACE to a multiscanner amyloid PET dataset and show that it retains the biological associations of age and apolipoprotein E (APOE) genotype with regional amyloid levels while reducing scanner differences.

RESEARCH IN CONTEXT

1. Systemic review: We conducted literature searches using Google Scholar and PubMed with the keywords “amyloid”, “PET”, “harmonization”, and “ComBat”. We also reviewed relevant citations in the papers that we identified through our literature search.

2. Interpretation: ComBat is not suitable for harmonizing multi‐site data with bimodal distributions such as amyloid PET measurements. Our method, PEACE, has a theoretical model that is in better alignment with multimodal data and yields more accurate harmonized values for unimodal data as well, suggesting its applicability beyond amyloid imaging data.

3. Future direction: PEACE should be tested on other neuroimaging data and in the context of harmonization of more challenging data sets that have multiple sources of systematic differences such as differences in scanner, radiotracer, and protocol.

2. METHOD

2.1. ComBat

We briefly review ComBat. Let $i\in \{1,2,\text{…},I\}$ indicate subject, $b_i\in \{1,2,\text{…},B\}$ the batch for subject i, and $k\in \{1,2,\text{…},K\}$ a biomarker or feature index. $y_{ik}$ is the value of biomarker k and $x_{il}$ is the value of covariate l for subject i.

The original ComBat model is

$$\begin{array}{ccc}\hfill y_{ik}& =& {\alpha }_k+\sum _l{\beta }_{kl}{x}_{il}+{\gamma }_{b_{i}k}+{\delta }_{b_{i}k}{\epsilon }_{ik}\hfill \end{array}$$ (1)

$$\begin{array}{ccc}\hfill {\epsilon }_{ik}& \sim & \mathcal{N}(0,{\sigma }_k^2),\hfill \end{array}$$ (2)

where γ and δ describe batch differences in biomarker level and noise variance, respectively, and have priors that help control their variances within a batch:

$$\begin{array}{ccc}\hfill {\gamma }_{bk}& \sim & \mathcal{N}\left(m_b,{\tau }_b^2\right),\hfill \end{array}$$ (3)

$$\begin{array}{ccc}\hfill {\delta }_{bk}& \sim & \mathrm{Inv}-\mathrm{Gamma}(u_b,v_b).\hfill \end{array}$$ (4)

$m_b,{\tau }_b,u_b$, and $v_b$ are fixed at their empirical Bayes (EB) estimates, whose identifiability is satisfied by deriving them under the constraint that ${\sum }_b{n}_b{\gamma }_{bk}=0$ for each k, where $n_b$ is the number of subjects in batch b. It is also possible to not use priors on γ and δ, which yields non‐EB ComBat.

The harmonized measurement, which removes batch effects but retains covariate effects, is given by

$$\begin{array}{ccc}\hfill y_{ik}^{\mathrm{ComBat}}& =& \frac{y_{ik}-\left({\widehat{\alpha }}_k+{\sum }_l{\widehat{\beta }}_{kl}{x}_{il}+{\widehat{\gamma }}_{b_{i}k}\right)}{{\widehat{\delta }}_{b_{i}k}}+{\widehat{\alpha }}_k+\sum _l{\widehat{\beta }}_{kl}{x}_{il},\hfill \end{array}$$ (5)

where $\widehat{\alpha },\widehat{\beta },\widehat{\gamma }$, and $\widehat{\delta }$ are the estimated parameters. In our analyses, we consider the first batch as the reference against which the remaining batches are harmonized. This is also known as modified ComBat (M‐ComBat). ¹⁸

2.2. PEACE

PEACE makes two substantial modifications to ComBat. First, we allow for the possibility that the data may follow a multimodal distribution by modeling the observations as a mixture of Gaussians. We incorporate this into the model by introducing latent variables $z_i\in \{1,2,\text{…},Z\}$ to indicate the cluster subject i belongs to. Each observation is assumed to be drawn from a normal distribution whose mean and variance depend on the latent cluster and batch. We want to be able to remove the effects of a batch without removing latent cluster effects; as a result, we need a model whose batch and latent cluster parameters are separable.

The PEACE model is given by

$$\begin{array}{ccc}\hfill y_{ik}& =& {\alpha }_{z_{i}k}+\sum _l{\beta }_{z_{i}kl}{x}_{il}+{\gamma }_{b_{i}k}+{\delta }_{b_{i}k}{\epsilon }_{ik},\hfill \end{array}$$ (6)

$$\begin{array}{ccc}\hfill {\epsilon }_{ik}& \sim & \mathcal{N}\left(0,{\sigma }_{z_{i}k}^2\right),\hfill \end{array}$$ (7)

$$\begin{array}{ccc}\hfill z_i& \sim & \mathrm{Categorical}\left({\mathit{\varphi }}_{b_i}\right).\hfill \end{array}$$ (8)

We seek to harmonize all observations to the first batch, so we fix ${\gamma }_{b=1,k}=0$ and ${\delta }_{b=1,k}=1\forall k$.

The second modification we make to ComBat is a fully Bayesian implementation of priors rather than an EB approach. We use the following priors and hyperpriors:

$$\begin{array}{cc}\hfill {\alpha }_{zk}& \sim \mathcal{N}\left({\overline{\mu }}_k,{\overline{s}}_{y_k}^2\right),\hfill \end{array}$$ (9)

$$\begin{array}{cc}\hfill {\beta }_{zkl}& \sim \mathcal{N}\left(0,{\overline{s}}_{y_k}^2/{\overline{s}}_{x_l}^2\right),\hfill \end{array}$$ (10)

$$\begin{array}{cccc}\hfill {\gamma }_{bk}& \sim \mathcal{N}\left(0,{\tau }_b^2\right)\hfill & & \mathrm{for}b>1,\hfill \end{array}$$ (11)

$$\begin{array}{cccc}\hfill {\delta }_{bk}& \sim \mathrm{Half}-\mathrm{Cauchy}\left(0,1\right)\hfill & & \mathrm{for}b>1,\hfill \end{array}$$ (12)

$$\begin{array}{cc}\hfill {\mathit{\varphi }}_b& \sim \mathrm{Dirichlet}\left({\mathbf{1}}_Z\right),\hfill \end{array}$$ (13)

$$\begin{array}{cc}\hfill {\tau }_b& \sim \mathrm{Exponential}\left({\overline{s}}_b^{-1}\right),\hfill \end{array}$$ (14)

$$\begin{array}{cc}\hfill {\sigma }_{zk}& \sim \mathrm{Exponential}\left({\overline{s}}_{y_k}^{-1}\right),\hfill \end{array}$$ (15)

where ${\overline{\mu }}_k=\frac{1}{I}{\sum }_i{y}_{ik}$ and ${\overline{s}}_{y_k}^2=\frac{1}{I-1}{\sum }_i{(y_{ik}-{\overline{\mu }}_k)}^2$ are the empirical mean and variance of the observations for feature k, respectively, and ${\overline{s}}_{x_l}^2$ is the variance of $x_l$. ${\mathit{\varphi }}_b$ is a vector in the unit $(Z-1)$‐dimensional simplex and indicates the probabilities of belonging to each latent cluster in batch b. Lastly,

$$\begin{array}{ccc}\hfill {\overline{s}}_b^2& =& \frac{1}{|{\mathrm{\Omega }}_b|K-1}\sum _k\sum _{i\in {\mathrm{\Omega }}_b}{\left(y_{ik}-{\overline{\mu }}_k\right)}^2\hfill \end{array}$$ (16)

is the variance of observations across all features in batch b, where ${\mathrm{\Omega }}_b=\{i\mid b_i=b\}$.

We selected the prior distributions for α, β, and σ based on the recommendations for weakly informative priors for Bayesian linear regression models implemented in Stan ¹⁹ [p. 124], omitting the 2.5 multiplier on the standard deviations of α and β to make the prior distributions narrower. This makes the priors more informative than those used in literature, ¹⁹ helping to guide model fitting by prioritizing batch‐agnostic parameters α and β before relying on the batch‐dependent parameters γ. Similarly, we assumed a normal prior for γ whose variance was modeled with an exponential distribution similar to that of σ. We selected the prior distribution for δ based on the recommendations for weakly informative prior alternatives to the inverse Gamma distribution in settings where distribution conjugacy is not required. ²⁰ We set the scale parameter of the half‐Cauchy distribution for δ to 1 to obtain a prior with approximately equal density in the intervals (0,1) and (1, ∞), reflecting that a priori, a given batch is approximately equally likely to have a smaller noise variance ($0<\delta <1$) or a greater noise variance ($\delta >1$) than that of the reference batch. We used the Dirichlet distribution as a prior for ϕ to ensure that the mixing coefficients summed to one within each batch, assuming an uninformative prior by setting the concentration parameter to a vector of ones.

We estimate model parameters using Hamiltonian Monte Carlo Markov chain (MCMC) sampling with T warm‐up iterations followed by T samples drawn from the posterior. The harmonized measurement at the t ^th posterior draw is given by

$$\begin{array}{ccc}\hfill {\stackrel{\sim }{y}}_{ik}& =& \frac{y_{ik}-\left({\alpha }_{z_{i}k}^{(t)}+{\sum }_l{\beta }_{z_{i}kl}^{(t)}{x}_{il}+{\gamma }_{b_{i}k}^{(t)}\right)}{{\delta }_{b_{i}k}^{(t)}}+{\alpha }_{z_{i}k}^{(t)}+\sum _l{\beta }_{z_{i}kl}^{(t)}{x}_{il},\hfill \end{array}$$ (17)

where ${\alpha }^{(t)},{\beta }^{(t)},{\gamma }^{(t)}$, and ${\delta }^{(t)}$ are the estimated parameters at the t ^th iteration. However, because the cluster that this subject belongs to is unknown, we cannot compute this quantity (unless ${\delta }_{b_{i}k}^{(t)}=1$). Instead, we compute the expected harmonized measurement given the observed data and the current parameter estimates by marginalizing over the clusters:

$$\begin{array}{ccc}\hfill E\left[{\stackrel{\sim }{y}}_{ik}\mid {\mathbf{y}}_i,{\mathit{\theta }}^{(t)}\right]& =& \sum _{z_i=1}^{Z}p\left(z_i\mid {\mathbf{y}}_i,{\mathit{\theta }}^{(t)}\right)\hfill \\ & & \times \left[\frac{y_{ik}-\left({\alpha }_{z_{i}k}^{(t)}+{\sum }_l{\beta }_{z_{i}kl}^{(t)}{x}_{il}+{\gamma }_{b_{i}k}^{(t)}\right)}{{\delta }_{b_{i}k}^{(t)}}+{\alpha }_{z_{i}k}^{(t)}+\sum _l{\beta }_{z_{i}kl}^{(t)}{x}_{il}\right],\hfill \end{array}$$ (18)

where

$$\begin{array}{ccc}\hfill p\left(z_i\mid {\mathbf{y}}_i,{\mathit{\theta }}^{(t)}\right)& =& \frac{{\varphi }_{b_i{z}_i}^{(t)}{\prod }_{k}p\left(y_{ik}\mid z_i,{\mathit{\theta }}^{(t)}\right)}{{\sum }_{z_i=1}^Z{\varphi }_{b_i{z}_i}^{(t)}{\prod }_{k}p\left(y_{ik}\mid z_i,{\mathit{\theta }}^{(t)}\right)}\hfill \end{array}$$ (19)

is the posterior probability that subject i belongs to cluster $z_i$, ${\mathbf{y}}_i$ is the vector of biomarker observations for subject i, and ${\mathit{\theta }}^{(t)}$ is the collection of estimates ${\alpha }^{(t)},{\beta }^{(t)},{\sigma }^{(t)},{\gamma }^{(t)}$, ${\delta }^{(t)}$, and ${\varphi }^{(t)}$. $E[{\stackrel{\sim }{y}}_{ik}\mid {\mathbf{y}}_i,{\mathit{\theta }}^{(t)}]$ is invariant to cluster ordering, meaning that it can be analyzed across iterations without having to ensure the compatibility of the cluster labels. We refer to $E[{\stackrel{\sim }{y}}_{ik}\mid {\mathbf{y}}_i,{\mathit{\theta }}^{(t)}]$ averaged over T iterations as $y_{ik}^{\mathrm{PEACE}}$.

2.3. Simulation experiments

We conducted two sets of simulation experiments. The first set evaluated the recovery of harmonized measurements as a function of the number of individuals I and the number of clusters Z. The second set investigated the robustness of harmonization to the relative proportion of clusters.

We fitted ComBat and PEACE to the simulated data. For ComBat, we used the neuroCombat R package ¹⁰ with the first batch set as the reference batch. We investigated ComBat with empirical Bayes (EB ComBat) and ComBat without priors (Non‐EB ComBat). For PEACE, we set the number of clusters to the true value of Z and used Stan ²¹ to perform Hamiltonian MCMC sampling. We compared the harmonized values estimated with ComBat and PEACE to their true values. We computed the root mean square error (RMSE) between the estimated harmonized measurements and the true measurements without batch effects for observations that are not in the reference batch:

$$\mathrm{RMSE}(\mathtt{Method})=\sqrt{\frac{1}{K{\sum }_{i|b_i\ne 1}1}{\sum }_{i|b_i\ne 1}{\sum }_k{\left(y_{ik}^{\mathrm{True}}-y_{ik}^{\mathtt{Method}}\right)}^2},$$ (20)

where Method is EB ComBat, Non‐EB ComBat, or PEACE.

2.3.1. Recovery of harmonized measurements as a function of I and Z

For the first set of experiments, we simulated datasets with $I=75,150,300,600$ individuals distributed equally across $B=3$ batches. We used Equations (6)–(15), where we set ${\overline{\mu }}_k=0$, ${\overline{s}}_{y_k}=5$, ${\overline{s}}_{x_l}=5$, and ${\overline{s}}_b=5$ $\forall k,l,b$ to simulate the data. These values were arbitrarily chosen and do not reflect the properties of any imaging modality. We set $L=1$ and sampled $x_i$ from a normal distribution with zero mean and unit standard deviation. We simulated two separate datasets with one ($Z=1$) or two ($Z=2$) clusters. For $Z=2$, instead of sampling ${\mathit{\varphi }}_b$ from a Dirichlet distribution, we manually picked ${\varphi }_1=[0.2,0.8]$, ${\varphi }_2=[0.3,0.7]$, and ${\varphi }_3=[0.4,0.6]$ for the purpose of simulating data.

2.3.2. Robustness of harmonization to relative proportion of clusters

To investigate the robustness of PEACE to the relative proportion of clusters, we simulated data for $I=150$ individuals split between $B=2$ batches and $Z=2$ clusters. The mixing coefficient for the first batch was fixed at 50%, and the mixing coefficient for the second batch (${\varphi }_{b=2,z=1}$) was one of the following: 10%, 30%, 50%, 70%, or 90%. Data were simulated for $K=36$ regions to reflect the statistical characteristics of regional amyloid PET data: the values of α, β, and σ were fixed at the intercept, regression coefficient for the age term, and residual noise standard deviation, respectively, estimated from linear regressions conducted among Pittsburgh compound B (PiB)− (for $z=1$) and among PiB+ (for $z=2$). We randomly sampled $\gamma$ from $\mathcal{N}(0,0.5^2)$ and $\delta$ from $\mathrm{Half}-\mathrm{Cauchy}(1,0.03)$ to generate batch effects that were consistent with the batch effects observed in our real dataset. In these experiments, the first cluster is analogous to the PiB− group, with a smaller noise variance, and the second cluster is analogous to the PiB+ group, with a greater noise variance. The mixing coefficient corresponds to the frequency of the first cluster.

2.4. Real data experiment

We demonstrate the application of PEACE to amyloid PET data acquired using the ¹¹C‐PiB radiotracer in the Baltimore Longitudinal Study of Aging. We scanned 79 participants on a General Electric (GE) Advance scanner and then on a Siemens High Resolution Research Tomograph (HRRT) at their next visit, which took place approximately 2.2 years later on average (range 0.7–6.6). Dynamic PiB data acquired over 70 min were analyzed using a simplified reference tissue model with spatial constraint ²² with cerebellar gray matter as the reference to calculate distribution volume ratio (DVR) images. ²³ The average DVR value in each cortical gray matter region was calculated using anatomical labels calculated with MUlti‐atlas region Segmentation utilizing Ensembles of registration algorithms and parameters (MUSE) ²⁴ on the corresponding structural MRI images.

We split the participants into two groups and assigned the first 40 participants to the GE Advance batch and the remaining 39 to the HRRT batch, using only the data for the corresponding scanner in the PEACE harmonization procedure. We then fitted the bimodal PEACE model with GE Advance as the reference batch using the mean DVR in 72 cortical regions of interest (ROIs) that are used to calculate global PiB DVR. We used age as a covariate in harmonization.

To verify that harmonization reduced scanner differences, we compared the PEACE result with the result of an affine transformation‐based harmonization for the 39 individuals in the second batch. This affine transformation‐based harmonization leveraged additional longitudinal data collected on each scanner (Appendix C). These affine transformation‐based harmonized values, which take into account expected changes in the PET measurements over the time interval between GE Advance and Siemens HRRT scans, were used as true values to compute the RMSE for PEACE results.

To verify that harmonization did not alter known biological associations, we examined the associations of age and APOE ε4 positivity with harmonized regional DVR using a separate linear regression model per ROI. We expected harmonization to not affect these associations. For this analysis, we focus on the results for two of the 72 ROIs: left and right precuneus, which are early amyloid accumulating regions. ²⁵

We also harmonized the same regional amyloid PET data using the spatial smoothing approach described by Joshi et al. ² (which involved smoothing the reconstructed GE Advance and Siemens HRRT PET scans with Gaussian kernels with different full width at half maximums calculated using scans of the Hoffman brain phantom to bring them to a common 8‐mm isotropic resolution prior to image analysis), EB ComBat, and Non‐EB ComBat. We computed RMSE using the affine transformation‐based harmonized values as true values, as described earlier. We also calculated the absolute error for each scan as the absolute difference from the affine transformation‐based harmonized value. Percent relative absolute error was computed by dividing the absolute error by the affine transformation‐based harmonized value and multiplying by 100.

2.5. Code availability

We provide the Stan code for the PEACE model in Appendices A and B.

3. RESULTS

3.1. Simulation experiments

3.1.1. Recovery of harmonized measurements as a function of I and Z

RMSEs for EB ComBat, non‐EB ComBat, and PEACE are shown in Table 1. In both the unimodal and bimodal simulations, PEACE outperformed ComBat.

TABLE 1.

RMSE for EB ComBat, Non‐EB ComBat, and PEACE as a function of sample size is shown for the simulation experiment with $Z=1$ (left) and $Z=2$ (right). PEACE achieves the lowest RMSE.

	$Z=1$				$Z=2$
	$I=75$	$I=150$	$I=300$	$I=600$	$I=75$	$I=150$	$I=300$	$I=600$
Unharmonized	15.07	16.69	17.37	19.35	33.58	28.6	29.88	32.92
EB ComBat	1.51	1.69	1.62	1.40	2.88	6.30	3.14	3.05
Non‐EB ComBat	0.76	1.32	1.00	0.61	2.57	6.22	3.06	2.99
PEACE	0.48	0.63	0.39	0.18	1.83	1.17	0.25	1.25

Abbreviations: EB ComBat, ComBat with empirical Bayes; Non‐EB ComBat, ComBat without empirical Bayes; PEACE, Probabilistic Estimation for Across‐batch Compatibility Enhancement; RMSE, root mean square error.

As an example, we present harmonized values for the first two biomarkers in the simulation experiment with $Z=2$ clusters and $I=600$ samples in Figure 1. ComBat underestimates the variance in the harmonized data, whereas bimodal PEACE yields a result closer to the true distribution.

FIGURE 1.

Simulation experiments investigating recovery of harmonized measurements. To illustrate the performance of ComBat and PEACE, we show the results for the simulation experiment with $Z=2$ clusters and $I=600$ samples. We present scatter plots of Biomarker 2 versus Biomarker 1. Color indicates batch and shape indicates cluster. Batch 1 is the reference batch, and therefore, measurements for subjects in this batch are not affected by harmonization by ComBat or PEACE. ComBat underestimates the variance in the harmonized data, whereas PEACE yields a result closer to the true distribution. PEACE, Probabilistic Estimation for Across‐batch Compatibility Enhancement.

3.1.2. Robustness of harmonization to the relative proportion of clusters

In simulation experiments investigating the robustness of harmonization to relative frequencies of the clusters, PEACE outperformed ComBat (Figure 2). RMSE was at its minimum for both ComBat and PEACE when the two batches had similar cluster frequencies. The increase in RMSE with mixing coefficient decreasing from 50% to 10% was similar for ComBat and PEACE. However, the increase in RMSE with mixing coefficient increasing from 50% to 90% was lower for PEACE than for ComBat.

FIGURE 2.

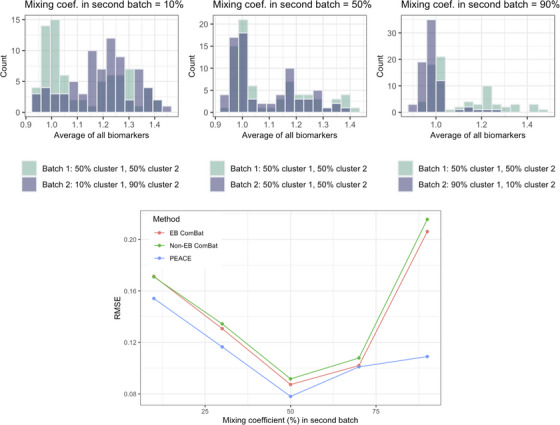
Simulation experiments investigating harmonization performance as a function of the mixing coefficient in the second batch. PEACE attains lower RMSE than ComBat and is robust to differences in cluster frequency between batches. Top: Histograms of simulated data. Data simulations were based on statistics observed in our PiB DVR dataset, with the two clusters being analogous to PiB– and PiB+ groups. The mixing coefficient was fixed at 50% in the first batch and was varied from 10% to 90% in 20 percentage point increments in the second batch. A low mixing coefficient corresponds to a lower frequency of the first cluster, which is analogous to the PiB– group. Bottom: RMSE of the harmonized values as a function of the mixing coefficient in the second batch (${\varphi }_{b=2,z=1}$). PEACE, Probabilistic Estimation for Across‐batch Compatibility Enhancement; PiB, ¹¹C‐Pittsburgh compound B; RMSE, Root mean square error.

3.2. Real data experiment

Participant characteristics are presented in Table 2. There were no statistically significant differences between batches in age, sex, race, or APOE ε4 positivity as assessed with Wilcoxon rank‐sum test for age and Fisher's exact test for the remaining variables. One participant in Batch 1 and two participants in Batch 2 were cognitively normal at the time of the GE Advance scan but developed mild cognitive impairment by the time of the Siemens HRRT scan. There were two participants in Batch 2 whose PiB group assignment based on the GE Advance scan was different from the PiB group assignment based on the Siemens HRRT scan (one converter and one reverter).

TABLE 2.

Participant characteristics. Age, PiB group, and diagnosis are reported at the time of the scan on the corresponding scanner. APOE genotyping was missing for one participant in each batch.

	Batch 1	Batch 2
	GE Advance	Siemens HRRT
	$N=40$	$N=39$
Age, median (IQR)	76 (71, 83)	79 (72, 84)
Female, n (%)	24 (60%)	24 (62%)
Race, n (%)
Asian or Pacific Islander	2 (5%)	2 (5%)
Black	5 (12%)	8 (21%)
White	33 (82%)	29 (74%)
APOE $\epsilon 4+$, n (%)	9 (23%)	13 (34%)
PiB+, n(%)	13 (32%)	12 (31%)
Diagnosis, n(%)
Cognitively normal	35 (88%)	36 (92%)
Mild cognitive impairment	4 (10%)	3 (7.7%)
Other impairment	1 (2.5%)	0

Abbreviations: GE, General Electric; HRRT, High Resolution Research Tomograph; IQR, interquartile range; PiB, 11C‐Pittsburgh compound B.

Figure S1 illustrates the longitudinal data used for the affine transformation‐based harmonization, which leverages within‐individual longitudinal trends to yield longitudinally consistent trajectories.

The overall RMSE across all 72 ROIs excluding the reference batch was 0.1736 for spatial smoothing, 0.0282 for EB ComBat, 0.0313 for non‐EB ComBat, and 0.0230 for PEACE. We calculated mean cortical DVR as the average of the 72 ROIs (Figure 3). Percent relative absolute error in mean cortical DVR was as high as 4.22% for ComBat (with absolute errors up to 0.055), while PEACE yielded percent relative absolute errors below 1.51% (with absolute errors up to 0.016).

FIGURE 3.

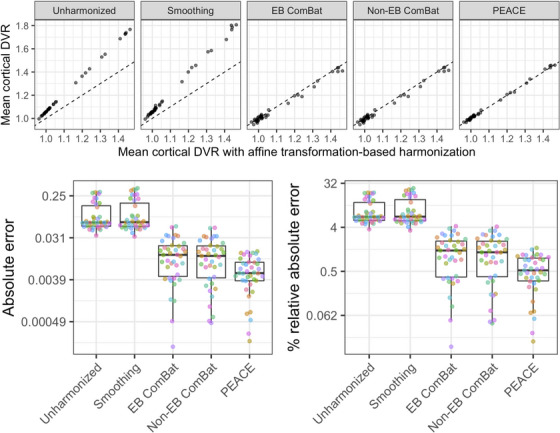
Harmonization results on PiB DVR data. 72 ROIs were used in ComBat and PEACE harmonization; for ease of presentation, we show the results for mean cortical DVR, which is calculated as the average of the 72 ROIs. Reference batch is excluded from the plots. PEACE yields the best agreement with affine‐transformed values, which are the expected values based on within‐individual longitudinal trends. Top: Agreement between harmonized values and affine‐transformed values. The dashed line is the identity line. Bottom: Absolute (left) and percent relative absolute error (right) between harmonized values and affine‐transformed values for each scan. log₂ scale is used for the y‐axes. Percent relative absolute error in mean cortical DVR was up to 4.22% for ComBat (with absolute errors up to 0.055), while PEACE yielded percent absolute errors below 1.51% (with absolute errors up to 0.016). DVR, distribution volume ratio; PEACE, Probabilistic Estimation for Across‐batch Compatibility Enhancement; PiB, ¹¹C‐Pittsburgh compound B; ROIs, regions of interest.

In linear regression analyses, both age and APOE ε4 positivity were associated with PEACE‐harmonized left ($\beta =0.0091$, SE = 0.0030, $p=0.0030$ for age; $\beta =0.13$, SE = 0.052, $p=0.015$ for APOE ε4) and right ($\beta =0.0080$, SE = 0.0031, $p=0.012$ for age; $\beta =0.11$, SE = 0.054, $p=0.045$ for APOE ε4) precuneus DVR.

4. DISCUSSION

We introduced PEACE, a fully Bayesian multimodal extension of ComBat, to account for differences across sites (or batches) in the means and noise variances of observations. Like ComBat, PEACE is also applicable to unimodal data, but unlike ComBat, PEACE can also be used for multimodal data such as amyloid PET measurements. As we showed in simulation experiments with unimodal outcomes, our fully Bayesian approach yields more accurate harmonized values compared to the EB and the non‐EB approaches employed in ComBat. Harmonization of bimodal data using ComBat, which assumes a unimodal distribution conditional on covariates, results in an underestimation of the variance in the harmonized estimates. We applied our method to regional amyloid PET imaging data acquired on two scanners and demonstrated that PEACE yielded harmonized values that agreed better with values expected based on previous longitudinal trends for each participant compared to ComBat. We also showed that PEACE harmonization did not remove the known effects of age or APOE ε4 positivity on amyloid levels, suggesting that PEACE can appropriately minimize scanner differences without altering true biological differences.

In simulation experiments, PEACE was robust to differences in the relative proportion of clusters between batches, since it was able to handle cases where cluster frequency was as low as 10%. The greater performance difference between PEACE and ComBat at high mixing coefficients compared to at low mixing coefficients likely stems from the fact that the noise variance was lower in the first cluster simulated in our experiments: with less noisy observations making up the greater proportion of the dataset, the PEACE model was able to estimate parameters more accurately.

In real data experiments, PEACE achieved a relative absolute error $\le 1.51\%$ for mean cortical PiB DVR for all scans. This is below the approximately 2% relative longitudinal change in global amyloid burden among amyloid accumulating individuals. ²⁶ On the other hand, the relative absolute error was as high as 4.22% for ComBat, exceeding the expected relative longitudinal change. These results suggest that PEACE harmonization may allow for better quantification of longitudinal change than ComBat, while longitudinal change might be wiped out with ComBat harmonization since the expected longitudinal change in amyloid burden is within the margin of error of ComBat.

There are several important advantages to using a fully Bayesian approach versus an EB approach. First, uncertainty in the harmonized values can be quantified by credible intervals, which are easily obtained by computing statistics across the MCMC samples. A bootstrapping‐based approach to accounting for parameter uncertainty in harmonization within the context of EB ComBat was proposed by Da‐ano et al., ²⁷ but this approach does not yield estimates of uncertainty in the harmonized values. Second, the search for an analytically tractable solution to minimize computation requirements in ComBat restricts the choice of priors to those that are conjugate to the assumed data distributions, and such conjugate priors may not be ideal. The inverse gamma prior, used in ComBat for the batch/site variance parameter, has been shown to exhibit irregularities, ²⁰ and recent Bayesian research has opted for other priors, such as exponential or Cauchy, that do not yield analytically tractable solutions but perform well under MCMC sampling.

Our proposed model and analyses have several limitations. PEACE incorporates a GMM, and as a result, its parameter estimation is susceptible to factors such as the relative frequency and separability of clusters. A fine‐tuned initialization might be necessary to obtain convergence and accurate results for challenging datasets. PEACE is based on several assumptions, including the independence of the batch effect from cluster assignment and the normality of residuals within each cluster and batch, which may not always be appropriate. We compared PEACE to ComBat, but further and more detailed comparison against other methods used in harmonization is necessary (a comprehensive review of harmonization methods applied to neuroimaging data is presented in literature ²⁸ ). In our amyloid PET dataset, scans were conducted on GE Advance and Siemens HRRT scanners at different visits separated on average by a couple of years, making it difficult to define a ground truth‐harmonized value against which we could compare our model results. The investigation of the performance of PEACE was limited to scanner differences in this analysis; further investigation is needed to determine whether PEACE can adequately harmonize across different amyloid radiotracers and acquisition protocols as well. Our study also has important strengths. We were able to leverage the available longitudinal PET data to define ground‐truth values against which to compare the harmonized Siemens HRRT values. We described a fully Bayesian method that can be fitted using existing MCMC sampling software. Our model can be applied to other neuroimaging data collected in studies of aging and AD, and the fully Bayesian approach provides a natural and easy way of quantifying the uncertainty in harmonization.

In conclusion, a fully Bayesian implementation of ComBat is within the computational power available to many researchers today, and our results suggest that such an approach is preferable over EB or non‐EB versions of ComBat. PEACE expands the class of biomarkers and measurements that can be satisfactorily harmonized beyond what is reasonable with ComBat.

CONFLICT OF INTEREST STATEMENT

The author has no conflicts of interest. Author disclosures are available in the supporting information.

Supporting information

Supporting Information

Supplementary material

Bilgel M. Probabilistic estimation for across‐batch compatibility enhancement for amyloid PET. Alzheimer's Dement. 2023;15:e12436. 10.1002/dad2.12436