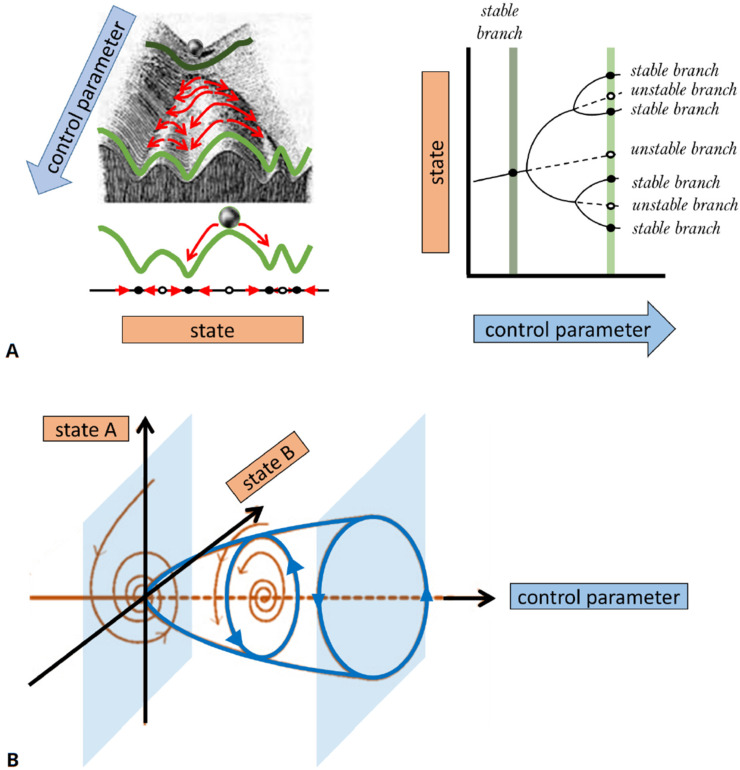
Figure 4. A basic description of bifurcation methodology.

(A) Phenomenological description of a bifurcation diagram using the ‘Waddington landscape.’. Left panel: The ‘state’ of a system is described by a single variable (axis labeled ‘state’). The evolution of the system with time (red arrows) is away from unstable states (open circles and mountain tops) and toward stable states (black circles and valleys). The directions of changes over time can be compressed into a flow diagram. The effect of a control parameter is shown as a shift in the geography of the hills and valleys. Right panel: A bifurcation diagram containing the information corresponding to the ‘Waddington landscape,’ where a stable state (solid line) becomes unstable (dashed line) to a pair of new stable states, a so-called ‘pitchfork’ bifurcation. The solid (dashed) lines correspond to valleys (mountain tops) in the left panel. The ‘bifurcation points’ mark parameter values, where small changes in a control parameter result in qualitative changes in the system’s behavior, e.g., when new solutions emerge at a branching point or their stability is changed. Bifurcation analysis allows us to map the ‘landscape’ of the underlying dynamical system and elucidates how various regimes of different behavior are related. In general, some branches of the bifurcation diagram may represent persistent oscillations, waves, or pulses in the system’s behavior. In (B), we schematically show a bifurcation to periodic oscillations (a.k.a. limit cycle solutions) for which the amplitude increases with distance from the bifurcation onset. Such instability is also known as a Hopf bifurcation and requires a system of at least two state variables (as opposed to a steady state pitchfork bifurcation demonstrated in (A) that may arise in models with a single variable). The shaded surfaces depict two selective phase-space projections spanned by the state variables at specific values of the control parameter, where the arrows correspond to temporal dynamics.