Effective moisture diffusivity prediction in two Portuguese fruit cultivars (Bravo de Esmolfe apple and Madeira banana) using drying kinetics data

Abstract

Air convective dehydration was performed at various temperatures (35 °C, 40 °C, 45 °C and 50 °C) using two types of fruits cultivars produced in different regions of Portugal: the Bravo de Esmolfe apple, from the Beiras province, and the Cavendish banana, from Madeira Island. The data collected were used to predict the effective moisture diffusion, which is a crucial input parameter in drying modeling and design. As expected, the values obtained in both falling drying rate periods detected for apples increased with an increase in drying temperature. The effective moisture diffusion in apples varied from 1.968 × 10⁻¹⁰ m² s⁻¹ at 35 °C to 4.013 × 10⁻¹⁰ m² s⁻¹ at 50 °C, for the first falling drying rate period, and from 0.9567 × 10⁻¹⁰ m² s⁻¹ at 35 °C to 3.328 × 10⁻¹⁰ m² s⁻¹ at 50 °C, for the second period. The dependence of effective moisture diffusion on temperature for bananas is similar, ranging from 1.572 × 10⁻¹⁰ to 2.627 × 10⁻¹⁰ m² s⁻¹ as the drying temperature changed from 35 to 50 °C.

1. Introduction

Generally, and inevitably in most cases, drying is an essential part of the unit operations of specific industrial processes for the production of a solid product. Industries such as food and agriculture, pharmaceuticals, ceramics, pulp and paper, among others, typically use at least one drying step, even if it is performed immediately before packaging. These different sectors and industries require the need of a dehydration, which is often accomplished using hot air stream (convective air drying) due to its associated advantages [[1], [2], [3], [4], [5], [6], [7]].

In the food industry, particularly in regards to vegetables and fruits, drying is crucial in increasing product stability and shelf life by reducing moisture content [5,8]. A low water activity prevents the grow of microorganisms and reduces final product weight, making it easier to transport [[9], [10], [11], [12], [13]]. Convective air drying is one of the traditional methodologies used in vegetables and fruits dehydration due to its low cost compared to other processes such as freeze drying [7]. Modern life with concerns about healthy and conscious eating has created a growing market niche that the industry is trying to address. Healthy ready-to-eat snacks, such as dehydrated fruit, are a good and tasty option for a quick meal. Dried apples and bananas are among the most accepted fruit snacks by consumers [14].

The “Bravo de Esmolfe” apple (Malus domestica Borkh. cv) is a Protected Designation of Origin (PDO) fruit from Portugal. These small to medium size apples with a pale yellow skin and a white interior are very tasty fruit and widely accepted by consumers [15]. Recently, Bravo de Esmolfe apple variety has received attention from a Portuguese scientific research team regarding its nutritional value, chemical characterization and bioactive properties [15]. Pires et al. [15] conducted a study with dried samples provided by a local company with a market position in the healthy snacks. They concluded that dried Bravo de Esmolfe apples have a balanced nutritional value (492 ± 1 kcal/100 g dry product) and are a source of bioactive compounds with antioxidant and antibacterial properties. Moreover, they are abundant in fructose (19.0 ± 0.2 g/100 g dry product), malic acid (1.36 ± 0.01 g/100 g dry product) and α-tocopherol (0.52 ± 0.02 mg/100 g dry product), making them a good source of these compounds.

Bananas, which are widely consumed all over the world, grows in tropical and subtropical regions and are known for their dietary and medicinal properties. Bananas are rich in bioactive compounds with antioxidant, anticancer, antidiabetic and antimicrobial properties [16]. In Madeira Island, bananas were first cultivated in the sixteenth century and presently are the most emblematic fruit of the island, with a production of over 20 thousand tons. The most important cultivar in the island is Dwarf Cavendish accounting for about 50–60% of the total banana production. The banana from Madeira Island is a fruit characterized to be small, sweet and tasty [17].

The food drying process is an essential step in preserving and extending the shelf life of various food products and it can impact the quality, texture, and nutritional value of the final product. Therefore, determining the kinetic parameters of the food drying process is essential to guarantee that the end product meets industry standards and consumer expectations. The transport of water throughout the solid during drying is a complex phenomenon that involves simultaneous heat and mass transfer [[18], [19], [20], [21], [22], [23]]. Several empirical or semiempirical models are available in the literature to predict the moisture content evolution during drying. However, for detailed and more realistic predictions the most important transport mechanisms must be identified and modeled. The accuracy of these models is dependent on good estimates of transport parameters used as input information, such as the effective moisture diffusivity, which is typically obtained from drying kinetic experiments [[24], [25], [26], [27], [28], [29], [30]]. The estimation of this parameter is essential for creating efficient and effective industrial dryers and allows the optimization of drying conditions, reduction of energy consumption and improvement of the final product quality.

The current study aimed to quantify the moisture transport parameter based on the drying kinetics data obtained at different temperatures for two fruits, apples and bananas, originating from Portugal mainland and Madeira Island, respectively. To the best of the authors' knowledge, the effective moisture diffusivity of “Bravo de Esmolfe” apples and Madeira Island bananas has not been published previously. Therefore, the authors hope to provide useful information for future drying model development for these two fruits.

2. Materials and methods

2.1. Materials and samples preparation

Fresh fruits were obtained from a local market and great care was taken to ensure that only Bravo de Esmolfe PDO apples and Cavendish bananas from Madeira Island with the indication of a product under protected designation of origin were purchased.

After peeling, the apples and bananas were cut using an electrical food slicer. Slices approximately 3 mm thick were obtained and after were cut into nearly rectangular shapes to ensure a uniform single layer covering the entire rectangular surface of the tray. The thickness slices was measured using a digital caliper and the individual values were obtained by averaging the measurements taken at various locations (four to five) of the rectangular shaped slice. Typically, 20 slices of fresh fruits were used for dimensional characterization in each experiment performed. The mean thickness obtained was (3.15 ± 0.05) mm for samples of fresh apples and (1.28 ± 0.19) mm for samples of fresh bananas.

To prevent enzymatic browning reactions in the fruits, the sample preparation, dimensional characterization and disposal in the tray were carried out as quickly as possible.

2.2. Convective hot air drying experiments

A laboratory tray dryer (Armfield Ltd, model UOP8) was used to conduct drying experiments at different temperatures for both fruits. Regulating an axial flow fan, the desired air flow rate was adjusted and the intensity of the heating elements near the tunnel entrance was changed to obtain different temperatures of the hot air stream in the convective drying kinetics experiments. The air stream temperature was changed in increments of 5 °C, ranging from 35 °C to 50 °C, and the constant air velocity in the drying chamber was 1.6 m s⁻¹.

Once the steady state conditions were reached in the dryer, the tray with the fruit samples was placed in the drying compartment and solid weight acquisition was started.

A weighing scale mounted on the top in the exterior of the dryer body, with an accuracy of ±0.1 g (digital balance OHAUS, Adventurer Pro AV8101), was used connected to a computer. The frequency of acquisition was 0.025 Hz (period of 40 s) and the decrease of the solid weight started to be recorded, using the Hyperterminal software, as soon as the drying experiment starts. The experiment was considered complete when no significant change in the solid weight was observed, indicating that an equilibrium with the air humidity of the drying stream had been reached.

For more details of the tray dryer equipment, experimental methodology and conditions, the description in Ref. [31] is recommended.

The dried fruit slices were also characterized dimensionally in terms of thickness using the same methodology described for the pre-drying samples. It should be noted that some samples became stuck to the base of the tray at the end of the drying process, resulting in a lower number of units measured. In particular, this happened with banana, and to avoid broken the dried samples the free depth of the tray was measured in several positions. The sample thickness was then obtained by subtracting the free depth from the total tray depth.

2.3. Drying kinetics data

The moisture content of solids is typically expressed on a dry basis, as the mass of water per mass of dry solid and is designated as X. The drying curve of a specific material is the plot of X versus t, which represents the moisture content evolution with time (t) in the solid throughout the drying process. Very often, by inspection this curve, different drying behaviors can be observed due to the effect of the internal structure of the product on mass transfer phenomena.

Frequently, after an initial transitory period, where the solid temperature adjusts to the air drying conditions, there is an period where drying is controlled by external moisture transport through air stream, after evaporation at the solid surface. During this period, the solid is dried at the maximum drying rate. Afterwards, the drying rate begins to decrease when the moisture internal transport becomes the dominant mechanism. This is dependent on the nature of the product being dried. The drying curve in this phase often exhibits one or two periods with different behavior [7].

Studies on drying food and agricultural products [[32], [33], [34], [35]] have shown that there is no constant drying rate period. In such cases, the internal mass transfer of moisture is the controlling mechanism throughout the entire drying process. The migration of moisture inside the solid is limited by several factors, such as capillary forces resulting from pressure gradients and liquid and/or vapor diffusion.

Numerous empirical and semi-theoretical models have been widely used to describe fruit and legumes behavior during dehydration. These models propose different equations that relate the moisture content of foodstuffs with time during the drying process. In a previous study [4], the authors investigated the drying kinetics behavior of Bravo de Esmolfe apples and Cavendish banana from Madeira Island. They found that apples had two falling drying rate periods and bananas did not have a constant drying rate period. Three different models were used to correlate the drying kinetics data obtained from experiments with Bravo de Esmolfe apples. Two of the models assumed a constant drying rate period followed by one falling drying rate period, one described by a polynomial function and the other by an exponential function. The third model considered a constant drying rate period followed by two falling drying rate periods. Based on commonly used correlation parameters to evaluate the statistical robustness of models, the authors concluded that the best performance was achieved with the scenario that included two periods of falling drying rate. However, the authors claimed the existence of a slight difference in behavior between the two falling drying rate periods and that a good fit to the data was also obtained when a unique falling drying rate period was described by a polynomial function.

The results reported by the authors [31] are consistent with findings from studies of other apple cultivars, such as Jonagold apples [36], and bananas, such as Dwarf Cavendish and Gros Michel [37].

2.4. Effective moisture diffusivity determination

Experimentally determining the effective moisture diffusion in solids through data recorded during a drying process is a common methodology and is based on the solution of Fick's second law. When considering the moisture transfer within the humid solid as one-dimensional (z direction) diffusion problem under non-steady state conditions in a slab with constant diffusion coefficient, Fick's second law can be expressed as follows:

$$\frac{\partial X}{\partial t}=D_{eff}\frac{{\partial }^{2}X}{\partial z^2}$$ (1)

where D_eff is the effective moisture diffusivity and X is the moisture content in the solid on dry basis.

Assuming:

• •initial distribution of moisture within the solid uniform, $X\left(t=0;z\right)=X_i$;
• •solid shrinkage during drying negligible;
• •external resistance to moisture transfer not significant;
• •fixed moisture content at the solid surface and equal to the value at the equilibrium stage with the drying air conditions ($X_e$);
• •temperature gradients in the solid matrix not noticeable;
• •symmetric moisture distribution around the plane at z = 0 during the drying process;

the solution of Eq. (1) is a well-known solution [38] given by an infinite series of term as:

$$\frac{X-X_i}{X_e-X_i}=1-\frac{4}{\pi }\sum _{n=0}^{\infty }\frac{{\left(-1\right)}^n}{\left(2n+1\right)}\cos \left[\frac{\left(2n+1\right)\pi }{2L}z\right]\exp \left[\frac{-{\left(2n+1\right)}^2{\pi }^2}{4L^2}{D}_{eff}t\right]$$ (2)

In Eq. (2), L represents the characteristic length for the geometry considered. If drying occurs from both surfaces of the humid solid layer, L stands for the solid half-thickness. However, when only one solid surface is exposed to the drying agent, the moisture is removed by evaporation only from that surface (as is the case of a humid solid drying in a tray drier) and L represents the thickness of the solid layer to be dried.

After spatial integration of Eq. (2), in order to obtain the mean moisture content in the sample ($\bar{X}$) it becomes:

$$M=\frac{\bar{X}-X_e}{X_i-X_e}=\frac{8}{{\pi }^2}\sum _{n=0}^{\infty }\frac{1}{{\left(2n+1\right)}^2}\exp \left[\frac{-{\left(2n+1\right)}^2{\pi }^2}{4L^2}{D}_{eff}t\right]$$ (3)

where, M is the moisture content ratio in the solid (a dimensionless parameter) and represents the ratio between the free moisture content at the instant t, $\left(\bar{X}-X_e\right)$, and the initial free moisture content, $\left(X_i-X_e\right)$.

As the series of infinite terms in Eq. (3) converge rapidly for the first term as drying time increases, usually is assumed that:

$$M\cong \frac{8}{{\pi }^2}\exp \left(\frac{-{\pi }^2}{4L^2}{D}_{eff}t\right)$$ (4)

This simplification is used very often to predicted D_eff from drying kinetics data [[39], [40], [41], [42], [43], [44]].

Applying logarithms to Eq. (4) a linear function between lnM and t was obtained with slope $\left(\raisebox{1ex}{$-{\pi }^2{D}_{eff}$}\!\left/ \!\raisebox{-1ex}{$4L^2$}\right.\right)$. Hence, D_eff can be calculated from the slope of the linear correlation between lnM and t obtained from the drying kinetics data acquired during the experiment performed at a specific temperature. Repeating this procedure with data collected for each temperature used in drying experiments, a set of D_eff values at different temperatures became available for each fruit tested.

It should be noted that Fick's second law of diffusion, Eq. (1), can only be applied during the drying step when the depletion of moisture from the solid is governed by the migration within the solid. At the present situation, $X_i$ corresponds to the critical moisture content in the solid at the transition between the constant and falling drying rate periods ($X_c$), the beginning of the drying phase governed by the moisture diffusion within the solid, and $X_i=X_c$. As referred before, two different falling drying rate periods were detected by the authors in a previous study [31] when the Bravo de Esmolfe apples were dried and the moisture content detected in the transitions were used to define the data used to determine D_eff for both periods. When no evidence of a constant drying rate period was observed, as in the case of banana, the Fick's second law of diffusion can be applied to the entire drying process, and all data collected during experiment is used to estimate D_eff.

The effective moisture diffusivity has a temperature-dependent relationship following an Arrhenius-type function,

$$D_{eff}=D_0\exp \left(\frac{-E_a}{RT}\right)$$ (5)

where D₀ is the Arrhenius factor, E_a is the activation energy, R is the ideal gas constant and T is the absolute temperature.

A linear form of Eq. (5) can be written as,

$$\ln D_{eff}=\ln D_0-\frac{E_a}{R}\times \frac{1}{T}$$ (6)

and the activation energy for moisture diffusion within the solid is obtained from the slope $\left(\raisebox{1ex}{$-E_a$}\!\left/ \!\raisebox{-1ex}{$R$}\right.\right)$ of the straight line when $\ln D_{eff}$ is plotted against $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$T$}\right.$.

3. Results and discussion

A set of experiments were conducted to estimate the key moisture transport parameter in drying processes, often used as input in modeling, the $D_{eff}$. For each type of fruit, the air drying stream was forced to pass tangentially over the tray surface with a fruit layer at the same velocity (1.6 m s⁻¹) and the temperature was adjusted from 35 to 50 °C, in increments of 5 °C.

In order to estimate the value of D_eff corresponding to each experiment performed with apple and banana, representations of lnM versus t were obtained. An example of this representation is shown in Fig. 1 A and B for each dried fruit. In all experiments, a good linear correlation was observed with coefficients of determination ranging from 0.9973 to 0.9891, for apples experiments and from 0.9906 to 0.9816 for the tests with bananas. By using the slopes of the best linear fit and Eq. (4), D_eff values were calculated and are shown in Table 1.

Fig. 1.

Representation of lnM versus t obtained from data acquired in the falling drying rate period(s) (FDRP) in experiments performed at 50 °C with: (A) Bravo de Esmolfe apple samples (red symbols correspond to the first falling drying rate period and the black symbols to the second one) and (B) Madeira banana samples. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

Table 1.

Effective moisture diffusivity values obtained for Bravo de Esmolfe apples (in the two falling drying rate periods) and for Madeira bananas drying at different temperatures. The activation energy is also depicted for both fruits.

	T (°C)	35	40	45	50
Apple	$D_{eff,1}$ × 1010 (m2 s−1)	1.968	2.951	3.122	4.013
	$D_{eff,2}$ × 1010 (m2 s−1)	0.9567	1.771	2.243	3.328
	$E_a$ (kJ mol−1)	36.40/65.93
Banana	$D_{eff}$ × 1010 (m2 s−1)	1.572	1.720	2.005	2.627
	$E_a$ (kJ mol−1)	27.95

Another aspect to be emphasized is the use of characteristic length in Eq. (4) to represent the moisture diffusion path. In fact, it was not possible to consider the shrinkage in the fruits and the dependence of D_eff on the characteristic length during the drying process, improving the predictions. However, an improvement can be made using a mean moisture diffusion path, using the average value obtained with the samples thickness before and after drying. With this purpose, the dried fruit samples were also dimensionally characterized using the methodology described in section 2.2. The dimensional characterization was carried out by taking 6 to 16 pieces of dried fruits. As expected, all mean values obtained from measurements with dried pieces were smaller than those of fresh fruit slices. The mean thickness for samples of apples after being dried was (1.28 ± 0.19) mm, representing an overall decrease of about 59%. The global shrinkage observed in the thickness of the fresh banana slices was similar (about 52%), with a reduction from (3.09 ± 0.06) mm to (1.50 ± 0.22) mm during the drying process.

As two falling drying rate periods were identified from the drying kinetics behavior of Bravo de Esmolfe apples [31], the effective moisture diffusion coefficient for each period was obtained according to Eq. (4). The characteristic length used for the moisture diffusion path during the first falling drying rate period was the average thickness between fresh and dried fruit samples. Instead, for the second falling drying rate period the thickness of dried fruit samples was used. The calculated D_eff values are in Table 1 and show that the resistance to moisture depletion from the interior of the fruit samples decreases with the increase in the temperature. For both fruits, D_eff values increased with the air stream temperature, as expected. The range of values obtained was from 1.968 × 10⁻¹⁰ m² s⁻¹ to 4.013 × 10⁻¹⁰ m² s⁻¹, for the first falling drying rate period ($D_{eff,1}$) and from 0.9567 × 10⁻¹⁰ m² s⁻¹ to 3.328 × 10⁻¹⁰ m² s⁻¹, for the second falling drying rate period ($D_{eff,2}$), when the temperature used to dry the Bravo de Esmolfe apples changed from 35 °C to 50 °C. For Madeira bananas, the correspondent range is from 1.572 × 10⁻¹⁰ m² s⁻¹ to 2.627 × 10⁻¹⁰ m² s⁻¹.

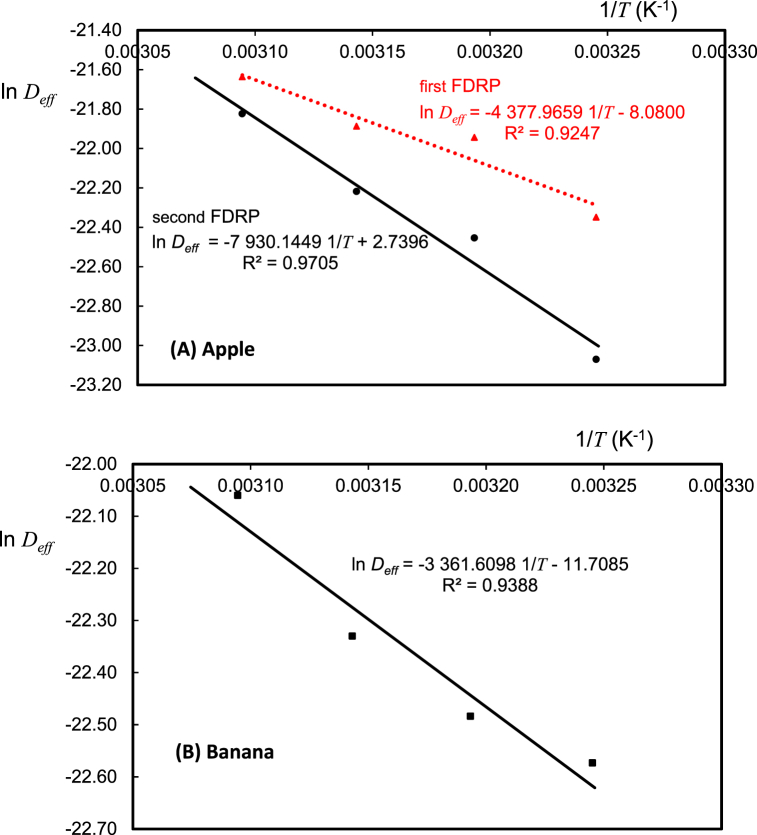
The activation energy for moisture diffusion in Bravo de Esmolfe apples and Madeira bananas, was quantified from the slope of the Arrhenius law (see Equation (6)) plots, lnD_eff versus 1/T, represented in Fig. 2 A and B. An activation energy of 36.40 and 65.93 kJ mol⁻¹, for first and second falling drying rate period, respectively, was obtained for apples indicating that a higher energy is required to initiate the moisture transfer within a thin-layer of this fruit compared to a thin-layer of bananas, for which an energy of 27.95 kJ mol⁻¹ is enough.

Fig. 2.

Plot of lnD_eff versus 1/T resulting from the Arrhenius-type relationship between effective moisture diffusivity and temperature for: (A) Bravo de Esmolfe apple samples at first and second falling drying rate periods (FDRP) and (B) Madeira banana samples.

The values of D_eff in food products range from 10⁻¹³ to 10⁻⁶ m² s⁻¹, with the majority (82%) concentrated in the region 10⁻¹¹ to 10⁻⁸ m² s⁻¹ [7]. From the analysis of a large volume of data collected from a significant number of scientific papers (almost two hundred) referring to more than one hundred food materials, Mujumdar [7] classified them into eleven food categories. In the nonporous and sugar containing foods category the observed values of the effective moisture diffusivities are low. In opposition, the porous food category was found to have higher values of moisture diffusivities. This observation is consistent with the results obtained in the present study for Bravo de Esmolfe apples and Madeira bananas (see Table 1). It should be noted that apples have a higher porosity structure compared to bananas. Using the four-parameters mathematical model proposed by Krokida and Maroulis [45], the porosity of Bravo de Esmolfe apples and Madeira bananas was predicted based on their initial moisture content (6.0 ± 0.6 kg/kg dry solid and 3.2 ± 0.2 kg/kg dry solid, respectively) and the corresponding values were 15.2% and 1.2%.

Despite the difficulty of making a direct comparison of D_eff with the values reported in the literature, due to the differences in the methodologies of estimation used, as well as the variation in the composition of the fruits which can be influenced by factors such as the variety, location of growing, harvesting period and ripening phase, some cases will be presented below.

Regarding the D_eff values obtained from the Bravo de Esmolfe apples, they were compared with results reported by some researcher teams for other varieties of apples, namely with the values for apple suggested in the Doulia et al. [46] database of apparent diffusivities of foods: 0.9–28 × 10⁻¹⁰ m² s⁻¹. As far as the authors are aware, the D_eff values for the apple variety used in the present study are not available in the bibliography.

Sacilik and Elicin [47] found values of D_eff in the range of 2.27 × 10⁻¹⁰ to 4.97 × 10⁻¹⁰ m² s⁻¹, when processing the data obtained from convective hot air drying experiments conducted at 40 °C, 50 °C and 60 °C, using a single layer with thicknesses of 5 and 9 mm of apples (cultivar Starking) grown through organic farming agriculture methods. These values are comparable to those obtained in the present study where the drying temperature of Bravo de Esmolfe apples was changed from 35 to 50 °C. However, it should be noted that apple samples variety used in the two studies were different.

Cruz et al. [48] investigated the drying kinetics and product quality of two commercial available apple cultivars (Golden Delicious and Granny Smith) in convective drying operations conducted at temperatures of 30 °C, 40 °C, 50 °C and 60 °C. The effective moisture diffusion of Golden Delicious cultivar increased with temperature from 4.22 × 10⁻¹⁰ to 1.44 × 10⁻⁹ m² s⁻¹ while for Granny Smith cultivar the corresponding increase was from 4.65 × 10⁻¹⁰ to 1.36 × 10⁻⁹ m² s⁻¹. Comparing directly the values obtained for drying at 40 and 50 °C with D_eff values presented in Table 1, they are greater for both cultivars. However, the discrepancies are higher for Golden Delicious (69.6% and 55.8%) than for Grand Smith cultivar (6.9% and 34.9%). Additionally, the authors reported an activation energy of 35.3 and 32.8 kJ mol^-1, respectively, for Golden Delicious and Grand Smith apples, indicating that to initiate the moisture diffusion process is energetically more favorable in those cultivars than in Bravo de Esmolfe apples where 36.40 kJ mol⁻¹ is required, corresponding to 3.0% and 9.9% more energy.

Beigi [49] investigated the drying of apple slices in a convective dryer at air temperatures of 50, 60 and 70 °C, and air velocities of 1, 1.5 and 2 m s⁻¹. The results showed that the effective moisture diffusivity was in the range of 6.75 × 10⁻¹⁰ – 1.28 × 10⁻⁹ m² s⁻¹ and increased with both the temperature and the drying air velocity.

A similar study was conducted for the Madeira banana, and the obtained D_eff values were compared with similar information available in the literature. However, once again, specific information for this banana variety was not found.

Nguyen and Price [45] explored the impact of different drying conditions on the drying kinetics of fresh Cavendish bananas (grown in North Queensland, Australia) in the temperature range of 30–70 °C (at 10 °C intervals) with a fixed air velocity of 1 m s⁻¹ The authors studied also the effect of the sample layer thickness. By applying the Arrhenius law to the drying of 1 cm slabs of ripe bananas, the D_eff values at 35, 40, 45 and 50 °C were calculated and compared with the ones presented in Table 1. The results showed that the D_eff values obtained in the current study were smaller than those found by Nguyen and Price [50] and the deviation increased for higher temperatures. At 35 °C, the deviation observed in D_eff values was relatively small (around 4%), but a difference of 32% was observed at higher temperatures. However, it should be noted that the authors used a mesh tray for drying samples and drying occurred on two surfaces.

Da Silva et al. [51] dried entire ripe bananas (Musa acuminata) using a hot air stream at four different temperatures: 40 °C, 50 °C, 60 °C and 70 °C. The authors used a liquid diffusion model, which took into account variable effective moisture diffusivity and shrinkage, to describe the drying process. Using the proposed equation for the relationship between moisture effective diffusivity and temperature, with E_a = 40.2 kJ mol⁻¹, deviations varying from 16.2 to 34.7% were obtained when compared with the values presented in Table 1. The results showed that the deviations tended to be higher when the drying temperature was lower.

After characterizing the drying process and identifying different drying rate periods, the determination of moisture diffusion parameters is a crucial input in modelling the process for optimizing the drying conditions. The results presented in this study are expected to contribute to future research on the impact of drying conditions on the nutritional quality of these fruits, making them more appealing for commercial purposes.

4. Conclusions

The Bravo de Esmolfe apple, from Beiras province of Portugal, and the Cavendish banana, from Madeira Island are highly valued for their sweet and delicious taste, and have great commercial potential as healthy snack when dehydrated. However, there is a lack of information about the crucial transport parameter widely used in dehydration modeling of these Portuguese cultivars of fruits.

The effective moisture diffusivity was obtained from drying data for both fruits as a function of the temperature used in the experiments. As expected, the transport parameter increases with temperature, ranging from 0.9567 × 10⁻¹⁰ to 4.013 × 10⁻¹⁰ m² s⁻¹ for apples and from 1.572 × 10⁻¹⁰ to 2.627 × 10⁻¹⁰ m² s⁻¹ for bananas, when the temperature used in experiments ranged from 35 to 50 °C. The effective moisture diffusivities obtained for apples dehydration in both falling drying rate periods, as previously determined by the authors, showed that the resistance to moisture depletion from the interior of the fruit samples was greater in the second falling drying rate.

Author contribution statement

M. N. Coelho Pinheiro: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper. Luis M. M. N. Castro: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interest's statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.