Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jun 29;62(27):10655–10664. doi: 10.1021/acs.inorgchem.3c01028

Structure and Ionic Conductivity of Li-Disordered Bismuth o-Thiophosphate Li60–3xBi16+x(PS4)36

Maximilian A Plass †,‡, Maxwell W Terban †, Tanja Scholz †, Igor Moudrakovski †, Viola Duppel †, Robert E Dinnebier †, Bettina V Lotsch †,‡,*
PMCID: PMC10336968  PMID: 37382207

Abstract

graphic file with name ic3c01028_0006.jpg

The structure of the first lithium-containing bismuth ortho (o)-thiophosphate was determined using a combination of powder X-ray, neutron, and electron diffraction. Li60–3xBi16+x(PS4)36 with x in the range of 4.1–6.5 possesses a complex monoclinic structure [space group C2/c (No. 15)] and a large unit cell with the lattice parameters a = 15.4866 Å, b = 10.3232 Å, c = 33.8046 Å, and β = 85.395° for Li44.4Bi21.2(PS4)36, in agreement with the structure as observed by X-ray and neutron pair distribution function analysis. The disordered distribution of lithium ions within the interstices of the dense host structure and the Li ion dynamics and diffusion pathways have been investigated by solid-state nuclear magnetic resonance (NMR) spectroscopy, pulsed field gradient NMR diffusion measurements, and bond valence sum calculations. The total lithium ion conductivities range from 2.6 × 10–7 to 2.8 × 10–6 S cm–1 at 20 °C with activation energies between 0.29 and 0.32 eV, depending on the bismuth content. Despite the highly disordered nature of lithium ions in Li60–3xBi16+x(PS4)36, the underlying dense host framework appears to limit the dimensionality of the lithium diffusion pathways and emphasizes once more the necessity of a close inspection of the structure–property relationships in solid electrolytes.

Short abstract

Different analytical techniques were used to characterize the structure and to investigate the ionic transport properties. The combination of these techniques allowed us to elucidate the complex structure of the first lithium-containing bismuth o-thiophosphate and provide insights into the electrochemical and ionic diffusion properties.

Introduction

The discovery of new materials is crucial for improving the performance of rechargeable energy devices such as lithium ion batteries (LIBs) used in hybrid or electric vehicle applications and to enhance their competitiveness with combustion engine vehicles. While liquid organic electrolytes are widely used in most commercial LIBs, all-solid-state batteries (ASSBs) composed of solid electrolytes are increasingly studied due to their advantageous properties such as nonflammability, high transference numbers, increased volumetric energy densities, and simplified cell architectures.1,2

Sulfides and thiophosphates are among the most promising solid inorganic electrolyte (SIE) candidates due to their comparatively high ionic conductivities3−6 of ≤10–2 S cm–1 and their mechanical softness, which make grain boundary-related losses less dominant. Another critical aspect of the development of new energy materials is the abundance and price of the raw materials7−9 used for their fabrication. While the most critical component in LIBs is usually lithium,10 the use of additional expensive elements or components for the large-scale synthesis of high-performance solid electrolytes (SEs) should be avoided to make ASSBs competitive for large-scale applications. In this context, bismuth can be a cheaper alternative compared to germanium or tin.7−9,11

Among all of the reported thiophosphates, only a few quaternary compounds containing bismuth have been reported so far. In terms of o-thiophosphates, only A3Bi(PS4)2 with A = K, Rb, Cs,12 Ag,13 or Tl,14 K1.5Bi2.5(PS4)3,15 Cs3Bi2(PS4)3,12 K9Bi(PS4)4,15 and A3Bi3(PS4)4 with A = K15 or Tl14 have been reported. The number of known bismuth hexathiohypodiphosphates is even smaller. Here, only Na0.16Bi1.28P2S612 and ABiP2S6 with A = K,16 Ag,17 and Tl14 have been reported to date. Among bismuth pyrothiophosphates, only three compounds with a composition of ABiP2S7 with A = K, Rb,12 and Tl14 and Tl2BiP2S718 are known.

Here, we report on the synthesis and characterization of the first lithium-containing quaternary bismuth o-thiophosphate Li60–3xBi16+x(PS4)36 showing a phase width of 4.1–6.5 for x. The structure of this new disordered lithium thiophosphate was determined with a combination of different powder diffraction techniques, and the diffusivity of the disordered lithium ions within the structure has been investigated using electrochemical impedance spectroscopy (EIS), pulsed field gradient nuclear magnetic resonance (PFG-NMR) spectroscopy, and bond valence sum (BVS) analysis.a

Experimental Section

Synthesis

Li60–3xBi16+x(PS4)36 was synthesized by mixing Li2S (Alfa Aesar, 99.9%), Bi (ChemPur, 99.99%, powder), and P4S10 (ChemPur, 98%) in stoichiometric ratios and adding a small excess of S8 (Merck, sublimed) in an agate mortar in an argon-filled glovebox. The reaction mixture was added to a glassy carbon crucible, transferred into a quartz ampule, and sealed under dynamic vacuum. The quartz ampules were heated under dynamic vacuum using a blow torch and flushed with argon several times to remove traces of O2 and H2O prior to use. The ampules were then heated to 700 °C for 24 h at a rate of 50 °C  h–1 and cooled to room temperature at the same rate.

Transmission Electron Microscopy

Bulk samples were ground, distributed onto a holey carbon/copper grid, and transferred into the microscope under a protective atmosphere. Transmission electron microscopy (TEM) was performed on a Philips CM 30 ST microscope (300 kV, LaB6 cathode) equipped with a spinning star device enabling the use of precession electron diffraction (PED).20 Simulations of the diffraction patterns were obtained with the JEMS software package.21

Raman Spectroscopy

Raman spectra of solid-state synthesized powders sealed in quartz capillaries were recorded using a Jobin Yvon Typ V 010 LabRAM single-grate spectrometer equipped with a double super razor edge filter and a Peltier-cooled charge-coupled device camera. The resolution of the spectrometer (grating, 1800 lines/mm) was 1 cm–1. The spectra were recorded in a quasi-backscattering geometry using the linearly polarized 632.817 nm line of a He/Ne gas laser. With the use of a filter, the power of the beam was adjusted to <1 mW, to protect against local heating. The spot size was 10 μm, focused by a 50× microscope objective onto the surface of the sample.

X-ray Diffraction

For laboratory powder X-ray diffraction (PXRD), the samples were sealed into glass capillaries having an inner diameter of 0.2 mm, which were mounted on Stoe Stadi-P diffractometers in Debye–Scherrer geometry, equipped with Ge(111) monochromators and Mythen2 1K Dectris detectors. The samples were measured using Ag-Kα1 and Cu-Kα1 radiation with wavelengths of 0.55941 and 1.54059 Å, respectively. The structure of lithium bismuth o-thiophosphate (LiBiPS) was determined from powder using TOPAS 6.0.22 The determination of the structure involved a peak fitting and an indexing of the obtained PXRD data, followed by a Pawley fit, and the preliminary structure model (without lithium) was finally obtained using a combination of the charge flipping and simulated annealing approach.23,24 After identification of the heavy atoms and PS4 tetrahedra, the latter were restrained as rigid bodies with the freedom to rotate, stretch, and bend to a certain degree. The background of the diffraction patterns was modeled by Chebychev polynomials of the tenth order and the peak profile by using the fundamental parameter approach implemented in TOPAS.25,26 The instrumental resolution function had been determined by a LeBail fit27 of a LaB6 or Si standard measurement prior to the experiments.

Neutron Powder Diffraction

Neutron powder diffraction (NPD) was performed at Spallation Neutron Source Powgen BL-11A of Oak Ridge National Laboratory. The measurements were conducted in a vanadium can having a diameter of 6 mm at 300 K using wavelengths of 0.8 and 2.665 Å. The refinement of the NPD data was performed with the use of a TOPAS template provided by Oak Ridge National Laboratory and as described by Dinnebier et al.28 Here, the preliminary structure model obtained from PXRD could be refined without the use of rigid bodies and including lithium positions. The obtained crystallographic data have been deposited at the Cambridge Crystallographic Data Centre (CCDC) with deposition number 2235620.

Pair Distribution Function Analysis

Pair distribution function (PDF) analysis29−31 was performed on neutron [neutron pair distribution function (nPDF)] and X-ray [X-ray pair distribution function (xPDF)] data. For nPDF analysis, the data sets collected at BL-11A were normalized and merged by averaging over a range of Q from 4.57 to 5.33 Å–1, where resolution differences were minimal, to give a high resolution at a lower Q and a high Qmax. The reduced structure function F(Q) was obtained using PDFgetN332 and further Fourier transformed using a Lorch function33 over a Qrange from 0.5 to 30.0 Å–1. The data for xPDF analysis were collected using a Stoe Stadi-P diffractometer with Ag-Kα1 radiation and 0.2 mm inner diameter glass capillary. Measurements collected at room temperature using a single Mythen2 1K Dectris detector over angular ranges of 0.405–125.145° (150 s/step), 40.5–125.145° (150 s/step), and 81.0–125.145° (300 s/step) were averaged and corrected for sample offset. An empty glass capillary was also measured and subtracted as a background. The xPDF data were further processed using PDFgetX334 within the xPDFsuite35 and Fourier transformed using a Qrange from 0.4 to 13.0 Å–1. An additional xPDF measurement was performed at 100 K using an Oxford Cryostream.

Structural co-refinements to the xPDF and nPDF data were carried out using PDFgui36 to refine lattice parameters a, b, c, and β, isotropic atomic displacement parameters (ADPs) for Bi, P, and S, Uiso fixed at 0.01 Å2 for Li, and site positions by C2/c symmetry (with low occupancy, disordered Li sites removed). A linear peak sharpening term δ137 was used to describe the effects of correlated motion at short distances, and the Qdamp parameter was refined for each data set to describe the effects of instrumental broadening.38,39

Solid-State Nuclear Magnetic Resonance Spectroscopy

All solid-state nuclear magnetic resonance (ssNMR) measurements were performed on a Bruker Avance-III wide bore spectrometer in a magnetic field of 9.4 T. 7Li (Larmor frequency of 155.5 MHz), 6Li (Larmor frequency of 58.9 MHz), and 31P (Larmor frequency of 161.9 MHz) magic angle spinning (MAS) nuclear magnetic resonance (NMR) spectra were recorded in 4 mm ZrO2 rotors using a Bruker BL4 MAS probe at a spinning speed of 10 kHz. Due to the high reactivity of the studied materials, they were flame sealed in pyrex MAS inserts for Bruker 4 mm rotors (Wilmad Glass, product DWGSK2576-1). Measurements on all 6Li, 7Li, and 31P were performed using a simple Bloch Decay excitation scheme with a total of 512–4096 accumulations in each experiment. The relaxation delays were ensured to be sufficiently long to provide for complete relaxation of magnetization and ensure quantitative measurements. The spectra were referenced to the external signals of 85% H3PO4 (31P) and a 1 M solution of LiCl (6Li and 7Li).407Li PFG-NMR diffusion measurements were conducted on a Bruker Avance-III 400 instrument equipped with a diff60 gradient probe (maximum gradient of 2900 G cm–1). Data were acquired using a stimulated echo sequence with diffusion times in the range of 10–200 ms and effective gradient durations of 1–3 ms. The measured echo-signal attenuation peaks were phase corrected, and the integrated areas were used to extract the diffusivities.

Electrochemical Measurements

The samples were ground, and 100–250 mg was pressed using a pressure of ∼0.5 GPa into pellets with a diameter of 5 mm and having a thickness of 1–3 mm. Then the pellets were contacted with stainless steel electrodes in a TSC Battery cell of RHD Instruments. The contact pressure during the measurements was applied with the use of a spring having a certain spring constant and, thus, applying pressures of 10 MPa. For EIS, the samples were measured with a Novocontrol Technologies NEISYS potentiostat, using amplitudes of 100 and 300 mV in a frequency range from 106  to 10 Hz between −10 and 60 °C within an argon-filled glovebox. To exclude contact-related issues of the measurements, a platinum film of ∼200 nm (Quorum Q150GB) was sputtered on some pellets before contact with stainless steel electrodes. For the low-temperature EIS, a pellet with a diameter of 8 mm, a thickness of 2.304 mm, and a mass of 328.3 mg was contacted with stainless steel electrodes in a custom-made Swagelok cell. Both the pressure for fabricating the pellet and the contact pressure during the measurement were adjusted similar to the values used for the high-temperature EIS measurements. The cell was placed on a copper table in a small box, which was filled with dry ice and liquid nitrogen for cooling and connected to the potentiostat. After the sample reached thermal equilibrium at −76 °C, EIS was measured using an amplitude of 100 mV in a frequency range from 106 to 10–1 Hz. Due to systematic errors, the data points at 49.53 and 52.99 Hz have been excluded from fitting. For direct current (dc) polarization measurements, a pellet with a diameter of 8 mm was prepared and mounted in a manner similar to that used for EIS in the custom-made Swagelok cell and measured by subsequently applying potentials from 0 to 1 V in steps of 200 mV for 3 h and collecting a data point every 100 ms. For a more precise determination of the ionic conductivity via dc, the same pellet was measured at 3 and 4 V for 5 min collecting one data point per 10 ms and held at this potential for a further 12 h with an acquisition time of 1 s.

Results and Discussion

Structure Determination

In the Li–Bi–P–S system, the synthesis led to dark red compounds, showing a compositional range of Li60–3xBi16+x(PS4)36. Only for values of x between 4.1 and 6.5 did the synthesized compounds contain minor impurities of Li4P2S6 of ∼1 wt %. An increase or decrease in bismuth or lithium content led to either the precipitation of BiPS4 or an increased fraction of an amorphous side phase, which formed Li4P2S6 upon heating.

Structure solution and characterization of LiBiPS drew on the use of several complementary techniques. While only the lattice parameters and a preliminary structure model could be identified on the basis of PXRD and electron diffraction (ED) (Figure S1), a complete structure model could be developed with the use of NPD and was verified with PDF analysis and the simulation of ED images (Figure S2). Exemplary Rietveld refinements of the PXRD and NPD data are given for Li44.4Bi21.2(PS4)36 in Figure 1 and Figure S3, and the crystallographic data are summarized in Table S1. Li60–3xBi16+x(PS4)36 possesses a large monoclinic unit cell with space group C2/c (No. 15), and the variation of the lattice parameters with the bismuth content is shown in Figure S4. The lattice parameters for Li60–3xBi16+x(PS4)36 with values of x between 4.1 and 6.5 range from 15.470 to 15.494 Å, from 10.337 to 10.271 Å, from 33.753 to 33.819 Å, and from 85.400° to 85.364° for a, b, c, and β, respectively. While a and c increase with x, b, β, and V decrease. Considering that for a replacement of one Bi3+ three Li+ need to be incorporated into the structure to maintain charge balance, this observation seems reasonable. The structure contains three bismuth, four phosphorus, 18 sulfur, and ≥10 lithium sites, all residing on general 8f positions and one phosphorus site at a 4e position (see Table S2).

Figure 1.

Figure 1

Open in a new tab

Rietveld refinements of Li44.4Bi21.2(PS4)36 for NPD data at 300 K using wavelengths of (a) 0.8 and (b) 2.665 Å and for PXRD data at room temperature using (c) Ag-Kα1 and (d) Cu-Kα1 radiation. The blue lines correspond to measured data, the red lines to simulated data, and the gray lines to their difference. The green ticks indicate the reflections of the main phase, whereas the purple ticks belong to minor impurities of Li4P2S6 (∼1 wt %) visible in only NPD.

The different lithium sites cannot be differentiated from one another in 6Li- and 7Li-ssNMR (see Figure S15a,b), where just one strong, asymmetric signal at −0.1  and 0.1 ppm and minor signals at 0.7 and 0.8 ppm, respectively, could be observed. In the 31P-ssNMR spectra depicted in Figure S15c, at least four overlapping signals at 83.7, 80.6, 77.7, and 73.7 ppm and two weak signals at 108.8 and 90.6 ppm were found. According to the determined structure of Li44.7Bi21.1(PS4)36 (see below), the four strong signals in the 31P ssNMR spectra can be assigned to the main phase, while the signal at ∼109 ppm can be assigned to a minor impurity of Li4P2S641 of ∼1 wt %. The remaining signal at ∼90.6 ppm with a fractional intensity of <1% may be ascribed to Li2S–P2S542 glass, glassy Li4P2S7,43 or amorphous BiPS4.

Phosphorus is found as regular 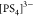Inline graphic-tetrahedra with P–S bond lengths in the range of 2.014–2.070 Å (see Table S3), and their existence within the structure could further be verified using Raman spectroscopy (see Figure S16). Here, the characteristic symmetric S–P–S stretching vibration of the PS4 tetrahedra44 at 413 cm–1 as well as the asymmetric stretching vibrations at ∼549 cm–1 could be identified.

Bismuth is coordinated by eight sulfide anions and forms distorted bicapped trigonal prisms, most likely induced by the stereochemically directing lone pair of BiIII (see Figure 2h–j) as observed in other compounds.12,13,15,44 The Bi–S bond distances range from 2.704 to 3.516 Å (see Table S3). While bismuth sites Bi1 and Bi2 show full occupation, Bi3 sites seem to be shared with lithium ions, showing site occupation factors (SOFs) of 0.65 and 0.35, respectively, thus leading to 21.18 bismuth ions per unit cell.

Figure 2.

Figure 2

Open in a new tab

(a)–(d) Structure of Li44.4Bi21.2(PS4)36 at different orientations. Layers formed by the BiS8- and PS4-polyhedra of (e) Bi1-, (f) Bi2-, and (g) Bi3-polyhedra. Coordination environments of (h) Bi1, (i) Bi2, and (j) Bi3 and connection of (k) the BiS8-polyhedra of Bi1 and Bi2 with the PS4-tetrahedra and (l) the Bi3-polyhedra. The phosphorus tetrahedra are colored orange. The different bismuth polyhedra are colored magenta, violet, and lavender for Bi1–Bi3, respectively. The lithium ions are coloerd green.

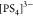According to the refinement of the NPD data, none of the remaining lithium sites show full occupation, reflecting its disordered nature. The bicapped trigonal prisms formed by Bi1 are on one hand connected via edge-sharing Inline graphic-tetrahedra and on the other via common corners to the Bi2- and Bi3-polyhedra. 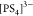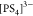While in Li44.4Bi21.2(PS4)36 the distorted bicapped Bi1- and Bi2-prisms are directly connected to four Inline graphic-tetrahedra via common edges (Figure 2k), two edge-sharing Bi3-polyhedra are connected to six Inline graphic tetrahedra, whereas two of them are bridging the two Bi3 polyhedra (Figure 2l). The Bi1 polyhedra are isolated from one another (Figure 2e), connected to Bi3 polyhedra by common edges and corners, and bridged by edge-sharing Inline graphic-tetrahedra. The Bi2-polyhedra are linked among each other via edge-sharing Inline graphic-tetrahedra along a and via common corners and bridging Inline graphic-tetrahedra along b and thus form a net-like layer in the a–b plane (Figure 2f). The host structure can be described as a stacking of the layers formed by the different bismuth polyhedra shown in Figure 2e–g in an ABCB-like fashion, which is illustrated in Figure 2. The lithium ions can be found within the interstices of this host framework without showing a regular coordination environment.

LiBiPS shows a structural relationship to lithium rare earth metal thiophosphates such as Li6Ln3(PS4)5 with Ln = Gd, Dy, Y, Yb, or Lu45,46 and Li9Ln2(PS4)5 with Ln = Nd,47 Ho,48 or Yb.46 Indeed, the title compound shows similar coordination environments for lithium, phosphorus, and the trivalent metal compared to Li6Ln3(PS4)5 and Li9Ln2(PS4)5, but due to the increased size of the bismuth cation as well as its stereochemically active lone pair, the arrangement slightly differs and can be seen as a structural fusion of the two different structure types of Li6Ln3(PS4)5 and Li9Ln2(PS4)5. A comparison of the PXRD patterns and the crystal structures are shown in Figures S7 and S8, respectively.

To verify the obtained structure and gain further insights into the local atomic environments, an analysis of the PDFs from neutron (nPDF) and X-ray (xPDF) total scattering data was performed. As with the diffraction analysis, differences in the weighting of the partial contributions to the total PDF for neutrons versus X-rays, as shown in Figure S9, also provide complementary sensitivities to different partial contributions to the structure.31 The associated F(Q) functions are listed in Figure S14.

Structure-independent peak fitting indicates a strong Gaussian distribution of the P–S bond lengths with a mean value of 2.0427(14) Å determined between the nPDF and xPDF data. The Bi–S distance distribution is more complex due to the various local environments, which may be explained by the stereochemically active lone pair of BiIII as observed in other compounds,12,13,15,44 but shows a maximum at ∼2.840(8) Å. A negative peak observed in the nPDF data at 2.450(4) Å, due to the negative neutron scattering length of 7Li, can be assigned to neighboring Li–S distances.

Analysis of the local structure was performed using the crystal structure model determined above. Comparison of the simulated PDF from the as-determined structure without modification to the ADPs indicates significantly increased local correlations (i.e., sharper pair distance distributions) between P–S, Li–S, Bi–S, and S–S nearest neighbor pairs that are unaccounted for in the Rietveld refinements (see Figure S10). A refinement of only the lattice parameters, thermal parameters, and a correction term for correlated motion δ1 still shows misfit over short distances, primarily in the range of 2.25–5.0 Å. Further refinement of the site positions gives a highly satisfactory fit and suggests the presence of local structuring between neighboring polyhedra that deviates slightly from the average structure, particularly with respect to the sulfur substructure. See Tables S4 and S5 for refinement details and Figure S11 for a comparison of structures. All partial contributions before and after refinement of the site positions are provided in Figure S12.

Assessment of the resulting Li–S partial PDF (Figure S13) suggests a roughly bimodal distance distribution with primary maxima at approximately 2.52 and 2.83 Å. This is in agreement with the Li–S partials for the related published structures of Li9Ln2(PS4)5, also showing a strong bimodal distribution, and Li6Ln3(PS4)5, showing a slightly more continuous distribution. LiBiPS appears to show a relatively larger population of Li at a longer coordination distance. More Li disorder in LiBiPS may be driven by the greater difficulty in forming optimal coordination environments in this system. As mentioned above, the different lithium sites could not be differentiated in ssNMR, and thus, the different contributions cannot be assigned to specific sites. However, the results do suggest that the lower occupation Li sites that appear with shortened Li–S bonds (≲2.3 Å) are likely a result of the representation of disorder in the average crystallographic density but not representative of the instantaneous local environments. We do not detect any distinct negative peaks at these shorter distances. Overall, the fits resulting from the refinements reaffirm the model obtained by the crystal structure solution and are shown in Figure 3.

Figure 3.

Figure 3

Open in a new tab

PDF analysis from (a and b) neutron data and (c and d) X-ray data for Li44.4Bi21.2(PS4)36 compared to the simulations resulting from co-refinements. Measured data (empty circles), simulation from the structure as determined from NPD with only lattice parameters, ADPs, and δ1 refined (red), and simulation with site positions refined (blue). The yellow and cyan lines correspond to the differences in the structure models obtained from the former and latter refinements, respectively.

Lithium Ion Conductivity and Diffusion Pathways

Structures with high levels of site disorder and low local coordination symmetry often show good ionic transport properties.49,50 We thus studied the lithium ion conductivity with the use of EIS. A discussion of the equivalent circuit models (ECMs) used for fitting the impedance data (Figure S17) as well as the obtained Nyquist and Bode plots (Figures S18–S21) and the respective values of the different equivalent circuit elements (ECEs) at a given temperature (Tables S6 and S7) can be be found in the Supporting Information, whereas the obtained Arrhenius graphs, ionic conductivities at 20 °C, and activation energies for ion diffusion are given in Figure 4. Li45Bi21(PS4)36 exhibits a total ionic conductivity of 1.6 × 10–6 S cm–1 at 20 °C with an activation energy of 0.29 eV. Increasing the bismuth content and accordingly decreasing the lithium content on the mixed Bi/Li sites appear to continuously decrease the ionic conductivity at 20 °C from 2.8 × 10–6 to 2.6 × 10–7 S cm–1. This may be ascribed to either a decreased number of available lithium ions as charge carriers or a further restriction of the diffusion pathways (narrowing or blocking) when the bismuth content is increased. The activation energy appears not to show a trend that is as pronounced, but overall behaves similarly and increases with bismuth content from 0.29 to 0.32 eV.

Figure 4.

Figure 4

Open in a new tab

Results of the EIS measurements. (a) Arrhenius graphs of the different Li60–3xBi16+x(PS4)36 species with their total ionic conductivities at 20 °C and (b) activation energies as a function of the SOF of Bi3 and of bismuth content x.

The lithium ion diffusion in Li44.4Bi21.2(PS4)36 has been additionally investigated with the use of 7Li-PFG-NMR spectroscopy, and the results are summarized in Figure S23. At 30 °C, T1 and T2 relaxation times were 6.04  and 5.99 × 10–4 s, respectively, leading to a tracer diffusion coefficient DtrNMR of 1.1 × 10–14 m2 s–1. An activation energy for lithium ion diffusion Ea of 0.40 eV was obtained from the PFG-NMR measurements. In contrast, the 7Li spin–lattice as well as spin–spin relaxation rates, which are typically associated with short-range (i.e., site-to-site) Li hopping processes, showed activation energies of 0.19 and 0.17 eV (see Figure S23a). These are comparable to other sulfide-based lithium ion conductors.51−54 The average diffusion length estimated from PFG-NMR measurements according to eq S12 is 661 Å at 30 °C and thus points to predominantly intracrystalline/bulk diffusion processes within the time frame of the measurement, whereas EIS accounts for intra- and intercrystalline ionic motion. The diffusion rate of an elementary jump was approximated according to eq S13. For a jump distance of 2.219 Å [obtained from softBV calculations (see below)], a jump rate of 1.33 × 106 s–1 was obtained. According to the Nernst–Einstein relationship given in eq S14, this results in an ionic conductivity σionNMR of 5.5 × 10–6 S cm–1 at 30 °C (compared to a σion of 1.8 × 10–6 S cm–1), when all lithium ions are assumed to be mobile (44.4 lithium ions per unit cell volume ≡ 8.242 × 1027 m–3) and with a Haven ratio of unity. The obtained values are only approximations because the real number of active charge carriers is unknown and the Haven ratio55 as well as the Bardeen–Herring tracer correlation factor56 can deviate from unity.

The electronic conductivity was estimated using chronoamperometric dc polarization measurements, as shown in Figure S22a. The equilibrium currents after successive potential steps of 200 mV showed an ohmic behavior as depicted in Figure S22b. Here, an electrical resistance Rel in the range from 5.7 × 108 to 8.7 × 108 Ω was observed for Li44.4Bi21.2(PS4)36, leading to electronic conductivities σeldc in the range from 3.4 × 10–10 to 5.2 × 10–10 S cm–1 at 20 °C . According to eq S9, the ionic transference number (tion) was estimated to be 0.999 (from a σion of 5.2 × 10–7 S cm–1 at 20 °C using the same pellet). The ionic conductivity from dc polarization measurements (σiondc) can be obtained from the initial currents Iinit of the polarization57,58 according to eqs S7 and S8. Because Iinit strongly depends on the acquisition time of the measurement, an additional fast dc polarization measurement with an acquisition time of 10 ms was used for a more precise determination of Iinit (see eqs S7 and S8). Here, ionic conductivities σion of ∼3.8 × 10–7 and ∼4.8 × 10–7 S cm–1 were observed for 3 and 4 V, respectively, which is in good agreement with the measured total ionic conductivity obtained from EIS (σionEIS = 5.2 × 10–7 S cm–1). The estimation of the conductivity diffusion coefficient Dσ via the Nernst–Einstein approximation given in eq S10 is ambiguous as long as the real number of charge carriers is unknown. Attempts to determine the charge carrier concentration with the use of transient ionic current (TIC)59,60 measurements were not successful.

To understand the origin of the unexpectedly low lithium ion conductivity, in spite of the high level of disorder, we investigated the Li ion percolation pathways using the softBV(61−63) approach. The obtained bond valence energy landscape (BVEL), the respective site energies along the most dominant diffusion trajectories, and the resulting energy barriers along these paths are shown in Figure 5 and Figure S24, respectively. Unlike the fast ion conductor Li10GeP2S12 (>10–2 S cm–1), which shows an extended quasi-three-dimensional network of lithium diffusion pathways at room temperature,64−66 the lithium ion percolation pathways in LiBiPS seem to extend predominantly in a helical pseudo-two-dimensional fashion (one-dimensional helical paths, which show a branching to two dimensions, but this is associated with higher energies or narrowing of the pathways) within the a–b plane. Therefore, layers with a higher density of low-energy pathways are observed (see the red and blue boxes in Figure 5b), which tend to be disconnected from each other along c. The different lithium percolation pathways in LiBiPS show energy barriers from 0.10 to 0.48 eV in the jump distance region of 1.6–3.8 Å as illustrated in Figure S24b. The restricted dimensionality of the diffusion pathways and their narrow/bottleneck-like nature are the reasons for the overall low ionic conductivities. For the related lanthanide compounds Li9Ho2(PS4)5 and Li15Ho7(PS4)12,48 one-dimensional pathways with energy barriers of 0.378 and 0.727 eV, respectively, and three-dimensional pathways with energy barriers of 0.471 and 0.838 eV, respectively, have been reported. Notably, in LiBiPS, the Bi3/Li3 sites are also part of the lithium ion percolation pathways (see the right side of Figure 5a) in the high-density region (blue box in Figure 5b) and a variation of the bismuth content thus alters the diffusion pathways along these sites. An increase in the bismuth content at these sites is expected to lead to a reduction in the number of opportunities for diffusion due to a blocking of diffusion pathways, thus resulting in a decrease in ionic conductivity as observed in EIS.

Figure 5.

Figure 5

Open in a new tab

BVEL of Li44.4Bi21.2(PS4)36 at different energy levels. (a) Overview of the BVEL within the unit cell. The magnifications of certain regions are provided to highlight some of the diffusion pathways. In the right panel, the mixed occupied Bi3/Li3 site is also shown, whereas all other atoms have been omitted. (b) BVEL for three unit cells along different orientations. The blue and red boxes highlight regions of high and low diffusion pathway densities, respectively. The BVEL is colored blue for low energies (−2.75 eV), and higher energies are colored green (−2.50 eV) and yellow (−2.25 eV).

Conclusion

With this work, we present the synthesis and in-depth characterization of the first lithium-containing bismuth o-thiophosphate Li60–3xBi16+x(PS4)36 with a compositional range of x from 4.1 to 6.5. The structure of LiBiPSs has been comprehensively examined with the use of PXRD, NPD, ED, xPDF and nPDF analysis, ssNMR, PFG-NMR spectroscopy, and Raman spectroscopy. Li60–3xBi16+x(PS4)36 compounds with values of x between 4.1 and 6.5 possesses a complex monoclinic structure [C2/c (No. 15)] and a large unit cell with the following parameters: a = 15.472–15.491 Å, b = 10.337–10.295 Å, c = 33.755–33.808 Å, and β = 85.394–85.378°. A structural relationship to Li6Ln3(PS4)5 and Li9Ln2(PS4)5 is evident, and the structure of the title compound can be described as a fusion of the latter structure types. The lithium ions are randomly distributed within the interstices formed by the densely connected bismuth thiophosphate host framework. In spite of the large degree of disorder, an overall low total ionic conductivity on the order of 2.6 × 10–7 to 2.8 × 10–6 S cm–1 at 20 °C was observed, with activation energies for ion diffusion in the range of 0.29–0.32 eV depending on the bismuth content of Li60–3xBi16+x(PS4)36. The low long-range diffusivity of the lithium ions [DtrNMR(30 °C) = 1.1 × 10–14 m2 s–1] can be ascribed to the predominantly one-dimensional and narrow helical diffusion pathways within the a–b plane. In spite of the disordered nature of the lithium ions, which generally is conducive to high ionic conductivities, the overall rather dense framework structure, paired with low-dimensional lithium diffusion pathways, gives rise to limited long-range diffusion of lithium ions.

Acknowledgments

This work was supported by the Max Planck Society, the BMBF cluster of competence FestBatt (03XPO177B), the DFG cluster of excellence e-conversion (EXC2089), and the Center for NanoScience. A portion of this research used resources at the Spallation Neutron Source (IPTS-25943), a U.S. Department of Energy Office of Science User Facility operated by the Oak Ridge National Laboratory. The authors thank Qiang Zhang for the NPD measurements and for his help in processing the data. Christian Schneider is acknowledged for fruitful discussions, Christine Stefani for PXRD, and Armin Schulz for Raman spectroscopy measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.3c01028.

  • Electron diffraction images and a comparison with the simulation, crystallographic information obtained from the Rietveld refinements of the NPD and PXRD data, 6Li-, 7Li-, and 31P-ssNMR spectra, Raman spectra, results of the softBV calculations, details about the electrochemical characterization like the fitting procedure, Nyquist, Bode and current versus voltage plots, and the results obtained from PFG-NMR spectroscopy (PDF)

Open access funded by Max Planck Society.

The authors declare no competing financial interest.

Footnotes

a

Note that a preprint of this article was uploaded to chemRxiv(19) prior to publication.

Supplementary Material

ic3c01028_si_001.pdf (16.9MB, pdf)

References

  1. Lotsch B. V.; Maier J. Relevance of solid electrolytes for lithium-based batteries: A realistic view. J. Electroceramics 2017, 38, 128–141. 10.1007/s10832-017-0091-0. [DOI] [Google Scholar]
  2. Zhang Z.; Shao Y.; Lotsch B.; Hu Y.-S.; Li H.; Janek J.; Nazar L. F.; Nan C.-W.; Maier J.; Armand M.; Chen L. New horizons for inorganic solid state ion conductors. Energy Environ. Sci. 2018, 11, 1945–1976. 10.1039/C8EE01053F. [DOI] [Google Scholar]
  3. Sun Y.; Suzuki K.; Hori S.; Hirayama M.; Kanno R. Superionic Conductors:Li10+δ[SnySi1-y]1+δP2−δ S12 with a Li10GeP2S12-type Structure in the Li3PS4–Li4SnS4–Li4SiS4 Quasi-ternary System. Chem. Mater. 2017, 29, 5858–5864. 10.1021/acs.chemmater.7b00886. [DOI] [Google Scholar]
  4. Bron P.; Johansson S.; Zick K.; Schmedt auf der Günne J.; Dehnen S.; Roling B. Li10SnP2S12: An Affordable Lithium Superionic Conductor. J. Am. Chem. Soc. 2013, 135, 15694–15697. 10.1021/ja407393y. [DOI] [PubMed] [Google Scholar]
  5. Kamaya N.; Homma K.; Yamakawa Y.; Hirayama M.; Kanno R.; Yonemura M.; Kamiyama T.; Kato Y.; Hama S.; Kawamoto K.; Mitsui A. A lithium superionic conductor. Nat. Mat. 2011, 10, 682–686. 10.1038/nmat3066. [DOI] [PubMed] [Google Scholar]
  6. Harm S.; Hatz A.-K.; Moudrakovski I.; Eger R.; Kuhn A.; Hoch C.; Lotsch B. V. Lesson Learned from NMR: Characterization and Ionic Conductivity of LGPS-like Li7SiPS8. Chem. Mater. 2019, 31, 1280–1288. 10.1021/acs.chemmater.8b04051. [DOI] [Google Scholar]
  7. Haynes W. M.; Lide D. R.; Bruno T. J.. CRC handbook of chemistry and physics, 94th ed.; CRC Press: Boca Raton, FL, 2014; Chapter Geophysics, p 2668. [Google Scholar]
  8. Andruleit H.; Elsner H.; Henning S.; Homberg-Heumann D.; Kreuz A.; Kuhn K.; Moldenhauer K.; Pein M.; Schauer M.; Schmidt S.; Schmitz M.; Sievers H.; Szurlies M.; Wilken H.. Deutschland - Rohstoffsituation 2019; 2020; p 156. [Google Scholar]
  9. Theler B.; Kauwe S. K.; Sparks T. D. Materials Abundance, Price, and Availability Data from the Years 1998 to 2015. Integr. Mater. Manuf. Innov. 2020, 9, 144–150. 10.1007/s40192-020-00173-5. [DOI] [Google Scholar]
  10. Turcheniuk K.; Bondarev D.; Amatucci G. G.; Yushin G. Battery materials for low-cost electric transportation. Mater. Today 2021, 42, 57–72. 10.1016/j.mattod.2020.09.027. [DOI] [Google Scholar]
  11. Mohan R. Green bismuth. Nat. Chem. 2010, 2, 336–336. 10.1038/nchem.609. [DOI] [PubMed] [Google Scholar]
  12. McCarthy T.; Kanatzidis M. G. Synthesis in molten alkali metal polythiophosphate fluxes. The new quaternary bismuth and antimony thiophosphates ABiP2S7 (A = K, Rb), A3M(PS4)2 (A = K, Rb, Cs; M = Sb, Bi), Cs3Bi2(PS4)3, and Na0.16Bi1.28P2S6. J. Alloys Compd. 1996, 236, 70–85. 10.1016/0925-8388(95)02161-2. [DOI] [Google Scholar]
  13. Fan Y.-H. H.; Zeng H.-Y. Y.; Jiang X.-M. M.; Zhang M.-J. J.; Liu B.-W. W.; Guo G.-C. C.; Huang J.-S. S. Thiophosphates containing Ag+ and lone-pair cations with interchiral double helix show both ionic conductivity and phase transition. Inorg. Chem. 2017, 56, 962–973. 10.1021/acs.inorgchem.6b02667. [DOI] [PubMed] [Google Scholar]
  14. Gave M. A.; Malliakas C. D.; Weliky D. P.; Kanatzidis M. G. Wide Compositional and Structural Diversity in the System Tl/Bi/P/Q (Q = S, Se) and Observation of Vicinal P-Tl J Coupling in the Solid State. Inorg. Chem. 2007, 46, 3632–3644. 10.1021/ic062465h. [DOI] [PubMed] [Google Scholar]
  15. Gave M. A.; Weliky D. P.; Kanatzidis M. G. New Potassium Bismuth Thiophosphates Including the Modulated K1.5Bi2.5(PS4)3. Inorg. Chem. 2007, 46, 11063–11074. 10.1021/ic701211a. [DOI] [PubMed] [Google Scholar]
  16. Manriquez V.; Galdámez A.; León D. R.; Garland M. T.; Jiménez M. Crystal structure of potassium bismuth hexathiodiphosphate, KBiP2S6. Z. Kristallogr. NCS 2003, 218, 151–252. 10.1524/ncrs.2003.218.2.151. [DOI] [Google Scholar]
  17. Gave M. A.; Bilc D.; Mahanti S. D.; Breshears J. D.; Kanatzidis M. G. On the lamellar compounds CuBiP2Se6, AgBiP2Se6 and AgBiP2S6. Antiferroelectric phase transitions due to cooperative Cu+ and Bi3+ ion motion. Inorg. Chem. 2005, 44, 5293–303. 10.1021/ic050357+. [DOI] [PubMed] [Google Scholar]
  18. McGuire M. A.; Reynolds T. K.; DiSalvo F. J. Exploring thallium compounds as thermoelectric materials: Seventeen new thallium chalcogenides. Chem. Mater. 2005, 17, 2875–2884. 10.1021/cm050412c. [DOI] [Google Scholar]
  19. Plaß M.; Terban M.; Scholz T.; Moundrakovski I.; Duppel V.; Dinnebier R.; Lotsch B. Structure and Ionic Conductivity of the Li-disordered Bismuth ortho-Thiophosphate Li60–3xBi16+x(PS4)36 with x = 4.2 to 6.7. chemRxiv 2023, 10.26434/chemrxiv-2023-gvxnv. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Vincent R.; Midgley P. Double conical beam-rocking system for measurement of integrated electron diffraction intensities. Ultramicroscopy 1994, 53, 271–282. 10.1016/0304-3991(94)90039-6. [DOI] [Google Scholar]
  21. Stadelmann P. EMS - a software package for electron diffraction analysis and HREM image simulation in materials science. Ultramicroscopy 1987, 21, 131–145. 10.1016/0304-3991(87)90080-5. [DOI] [Google Scholar]
  22. Coelho A. A. TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. 10.1107/S1600576718000183. [DOI] [Google Scholar]
  23. Coelho A. A. Whole-profile structure solution from powder diffraction data using simulated annealing. J. Appl. Crystallogr. 2000, 33, 899–908. 10.1107/S002188980000248X. [DOI] [Google Scholar]
  24. Coelho A. A. Indexing of powder diffraction patterns by iterative use of singular value decomposition. J. Appl. Crystallogr. 2003, 36, 86–95. 10.1107/S0021889802019878. [DOI] [Google Scholar]
  25. Cheary R. W.; Coelho A. A fundamental parameters approach to X-ray line-profile fitting. J. Appl. Crystallogr. 1992, 25, 109–121. 10.1107/S0021889891010804. [DOI] [Google Scholar]
  26. Cheary R.; Coelho A.; Cline J. Fundamental parameters line profile fitting in laboratory diffractometers. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 1. 10.6028/jres.109.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Le Bail A.; Duroy H.; Fourquet J. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. 10.1016/0025-5408(88)90019-0. [DOI] [Google Scholar]
  28. Dinnebier R. E.; Leineweber A.; Evans J. S.. Rietveld Refinement; De Gruyter, 2018. [Google Scholar]
  29. Egami T.; Billinge S.. Underneath the Bragg peaks: structural analysis of complex materials, 2nd ed.; Newnes, 2012; p 422. [Google Scholar]
  30. Billinge S. J. L.International Tables for Crystallography, Vol. H; 2019; Chapter 5.7, pp 649–672. [Google Scholar]
  31. Terban M. W.; Billinge S. J. L. Structural analysis of molecular materials using the pair distribution function. Chem. Rev. 2022, 122, 1208–1272. 10.1021/acs.chemrev.1c00237. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Juhás P.; Louwen J. N.; van Eijck L.; Vogt E.; Billinge S. PDFgetN3: atomic pair distribution functions from neutron powder diffraction data using ad hoc corrections. J. Appl. Crystallogr. 2018, 51, 1492–1497. 10.1107/S1600576718010002. [DOI] [Google Scholar]
  33. Lorch E. Neutron diffraction by germania, silica and radiation-damaged silica glasses. J. Phys. C: Solid State Phys. 1969, 2, 229–237. 10.1088/0022-3719/2/2/305. [DOI] [Google Scholar]
  34. Juhás P.; Davis T.; Farrow C.; Billinge S. PDFgetX3: a rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Crystallogr. 2013, 46, 560–566. 10.1107/S0021889813005190. [DOI] [Google Scholar]
  35. Yang X.; Juhas P.; Farrow C. L.; Billinge S. J. L.. xPDFsuite: an end-to-end software solution for high throughput pair distribution function transformation, visualization and analysis; 2014. [Google Scholar]
  36. Farrow C. L.; Juhas P.; Liu J. W.; Bryndin D.; Božin E. S.; Bloch J.; Proffen T.; Billinge S. J. L. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys.: Condens. Matter 2007, 19, 335219. 10.1088/0953-8984/19/33/335219. [DOI] [PubMed] [Google Scholar]
  37. Jeong I.-K.; Proffen T.; Mohiuddin-Jacobs F.; Billinge S. J. L. Measuring Correlated Atomic Motion Using X-ray Diffraction. J. Phys. Chem. A 1999, 103, 921–924. 10.1021/jp9836978. [DOI] [Google Scholar]
  38. Qiu X.; Božin E. S.; Juhas P.; Proffen T.; Billinge S. J. L. Reciprocal-space instrumental effects on the real-space neutron atomic pair distribution function. J. Appl. Crystallogr. 2004, 37, 110–116. 10.1107/S0021889803026670. [DOI] [Google Scholar]
  39. Olds D.; Saunders C. N.; Peters M.; Proffen T.; Neuefeind J.; Page K. Precise implications for real-space pair distribution function modeling of effects intrinsic to modern time-of-flight neutron diffractometers. Acta Crystallogr. A 2018, 74, 293–307. 10.1107/S2053273318003224. [DOI] [PubMed] [Google Scholar]
  40. Harris R. K.; Becker E. D.; Cabral de Menezes S. M.; Goodfellow R.; Granger P. NMR nomenclature. Nuclear spin properties and conventions for chemical shifts (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 1795–1818. 10.1351/pac200173111795. [DOI] [PubMed] [Google Scholar]
  41. Neuberger S.; Culver S. P.; Eckert H.; Zeier W. G.; Schmedt auf der Günne J. Schmedt Auf Der Günne, J. Refinement of the crystal structure of Li4P2S6 using NMR crystallography. Dalton Trans. 2018, 47, 11691–11695. 10.1039/C8DT02619J. [DOI] [PubMed] [Google Scholar]
  42. Eckert H.; Zhang Z.; Kennedy J. H. Structural Transformation of Non-Oxide Chalcogenide Glasses. The Short-Range Order of Li2S–P2S5 Glasses Studied by Quantitative 31P and 6,7Li High-Resolution Solid-State NMR. Chem. Mater. 1990, 2, 273–279. 10.1021/cm00009a017. [DOI] [Google Scholar]
  43. Schmedt auf der Günne J.; Eckert H. High-Resolution Double-Quantum 31P NMR: A New Approach to Structural Studies of Thiophosphates. Chem. Eur. J. 1998, 4, 1762–1767. . [DOI] [Google Scholar]
  44. Tiwari D.; Alibhai D.; Cherns D.; Fermin D. J. Crystal and Electronic Structure of Bismuth Thiophosphate, BiPS4: An Earth-Abundant Solar Absorber. Chem. Mater. 2020, 32, 1235–1242. 10.1021/acs.chemmater.9b04626. [DOI] [Google Scholar]
  45. Müller C.; Jörgens S.; Mewis A. Neue Thiophosphate: Die Verbindungen Li6Ln3(PS4)5 (Ln: Y, Gd, Dy, Yb, Lu) und Ag3Y(PS4)2. Z. Anorg. Allg. Chem. 2007, 633, 1633–1638. 10.1002/zaac.200700065. [DOI] [Google Scholar]
  46. Lange P. L.; Schleid T. Li9Yb2[PS4]5 and Li6Yb3[PS4]5: two lithium-containing ytterbium(III) thiophosphates(V) revisited. Z. Naturforsch. 2021, 76, 281–291. 10.1515/znb-2021-0023. [DOI] [Google Scholar]
  47. Komm T.; Schleid T. Li9Nd2[PS4]5: A new lithium lanthanoid(III) thiophosphate(V). J. Alloys Compd. 2006, 418, 106–110. 10.1016/j.jallcom.2005.09.089. [DOI] [Google Scholar]
  48. Lange P. L.; Komm T.; Schleid T. Two Hitherto Unknown Lithium Holmium(III) Ortho -Thiophosphates(V): Li9Ho2[PS4]5 and Li15Ho7[PS4]12. Z. Anorg. Allg. Chem. 2021, 647, 2113–2121. 10.1002/zaac.202100203. [DOI] [Google Scholar]
  49. Kaup K.; Assoud A.; Liu J.; Nazar L. F. Fast Li-Ion Conductivity in Superadamantanoid Lithium Thioborate Halides. Angew. Chemie Int. Ed. 2021, 60, 6975–6980. 10.1002/anie.202013339. [DOI] [PubMed] [Google Scholar]
  50. Harm S.; Hatz A.-K.; Schneider C.; Hoefer C.; Hoch C.; Lotsch B. V. Finding the Right Blend: Interplay Between Structure and Sodium Ion Conductivity in the System Na5AlS4–Na4SiS4. Front. Chem. 2020, 8, 90. 10.3389/fchem.2020.00090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Kuhn A.; Gerbig O.; Zhu C.; Falkenberg F.; Maier J.; Lotsch B. V. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 2014, 16, 14669–14674. 10.1039/C4CP02046D. [DOI] [PubMed] [Google Scholar]
  52. Hogrefe K.; Minafra N.; Zeier W. G.; Wilkening H. M. R. Tracking Ions the Direct Way: Long-Range Li + Dynamics in the Thio-LISICON Family Li4 MCh4 (M = Sn, Ge; Ch = S, Se) as Probed by 7Li NMR Relaxometry and 7Li Spin-Alignment Echo NMR. J. Phys. Chem. C 2021, 125, 2306. 10.1021/acs.jpcc.0c10224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Hogrefe K.; Minafra N.; Hanghofer I.; Banik A.; Zeier W. G.; Wilkening H. M. R. Opening Diffusion Pathways through Site Disorder: The Interplay of Local Structure and Ion Dynamics in the Solid Electrolyte Li6+xP1–xGexS5I as Probed by Neutron Diffraction and NMR. J. Am. Chem. Soc. 2022, 144, 1795–1812. 10.1021/jacs.1c11571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Zhang Z.; Kennedy J. H.; Thompson J.; Anderson S.; Lathrop D. A.; Eckert H. Competitive network modification in non-oxide chalcogenide glasses structural and motional properties of glasses in the system Li2S-P2S5-B2S3 studied by multinuclear NMR techniques. Appl. Phys. A Solids Surfaces 1989, 49, 41–54. 10.1007/BF00615463. [DOI] [Google Scholar]
  55. Murch G. E. The haven ratio in fast ionic conductors. Solid State Ionics 1982, 7, 177–198. 10.1016/0167-2738(82)90050-9. [DOI] [Google Scholar]
  56. Bardeen J.; Herring C.. Diffusion in Alloys and the Kirkendall Effect. In Imperfections in Nearly Perfect Crystals; Shockley W., Hollomon J. H., Mauerer R., Seitz F., Eds.; John Wiley & Sons, Inc., 1952; pp 261–288. [Google Scholar]
  57. Maier J.Physical Chemistry of Ionic Materials: Ions and Electrons in Solids; John Wiley & Sons, Ltd.: Chichester, U.K., 2004. [Google Scholar]
  58. Senocrate A.; Moudrakovski I.; Kim G. Y.; Yang T.-Y.; Gregori G.; Grätzel M.; Maier J. The Nature of Ion Conduction in Methylammonium Lead Iodide: A Multimethod Approach. Angew. Chem. 2017, 129, 7863–7867. 10.1002/ange.201701724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Agrawal R.; Kathal K.; Gupta R. Estimation of energies of Ag+ ion formation and migration using transient ionic current (TIC) technique. Solid State Ionics 1994, 74, 137–140. 10.1016/0167-2738(94)90203-8. [DOI] [Google Scholar]
  60. Watanabe M.; Sanui K.; Ogata N.; Kobayashi T.; Ohtaki Z. Ionic conductivity and mobility in network polymers from poly(propylene oxide) containing lithium perchlorate. J. Appl. Phys. 1985, 57, 123–128. 10.1063/1.335386. [DOI] [Google Scholar]
  61. Chen H.; Adams S. Bond softness sensitive bond-valence parameters for crystal structure plausibility tests. IUCrJ 2017, 4, 614–625. 10.1107/S2052252517010211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Chen H.; Wong L. L.; Adams S. SoftBV – a software tool for screening the materials genome of inorganic fast ion conductors. Acta. Crystallogr. B. Struct. Sci. Cryst. Eng. Mater. 2019, 75, 18–33. 10.1107/S2052520618015718. [DOI] [PubMed] [Google Scholar]
  63. Wong L. L.; Phuah K. C.; Dai R.; Chen H.; Chew W. S.; Adams S. Bond Valence Pathway Analyzer–An Automatic Rapid Screening Tool for Fast Ion Conductors within softBV. Chem. Mater. 2021, 33, 625–641. 10.1021/acs.chemmater.0c03893. [DOI] [Google Scholar]
  64. Kuhn A.; Gerbig O.; Zhu C.; Falkenberg F.; Maier J.; Lotsch B. V. A new ultrafast superionic Li-conductor: ion dynamics in Li11Si2PS12 and comparison with other tetragonal LGPS-type electrolytes. Phys. Chem. Chem. Phys. 2014, 16, 14669–14674. 10.1039/C4CP02046D. [DOI] [PubMed] [Google Scholar]
  65. Kuhn A.; Duppel V.; Lotsch B. V. Tetragonal Li10GeP2S12 and Li7GePS8 – exploring the Li ion dynamics in LGPS Li electrolytes. Energy Environ. Sci. 2013, 6, 3548–3552. 10.1039/c3ee41728j. [DOI] [Google Scholar]
  66. Weber D. A.; Senyshyn A.; Weldert K. S.; Wenzel S.; Zhang W.; Kaiser R.; Berendts S.; Janek J.; Zeier W. G. Structural Insights and 3D Diffusion Pathways within the Lithium Superionic Conductor Li10GeP2S12. Chem. Mater. 2016, 28, 5905–5915. 10.1021/acs.chemmater.6b02424. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ic3c01028_si_001.pdf (16.9MB, pdf)

Articles from Inorganic Chemistry are provided here courtesy of American Chemical Society

RESOURCES