Abstract
Low-cost air quality monitors are increasingly being deployed in various indoor environments. However, data of high temporal resolution from those sensors are often summarized into a single mean value, with information about pollutant dynamics discarded. Further, low-cost sensors often suffer from limitations such as a lack of absolute accuracy and drift over time. There is a growing interest in utilizing data science and machine learning techniques to overcome those limitations and take full advantage of low-cost sensors. In this study, we developed an unsupervised machine learning model for automatically recognizing decay periods from concentration time series data and estimating pollutant loss rates. The model uses k-means and DBSCAN clustering to extract decays and then mass balance equations to estimate loss rates. Applications on data collected from various environments suggest that the CO2 loss rate was consistently lower than the PM2.5 loss rate in the same environment, while both varied spatially and temporally. Further, detailed protocols were established to select optimal model hyperparameters and filter out results with high uncertainty. Overall, this model provides a novel solution to monitoring pollutant removal rates with potentially wide applications such as evaluating filtration and ventilation and characterizing indoor emission sources.
Keywords: k-means clustering, DBSCAN, low-cost sensors, PM2.5, CO2, air change rate
Short abstract
Huge amounts of indoor air quality data are being generated but not fully utilized. This study develops a model that automatically processes pollutant concentration data to estimate loss rates.
1. Introduction
Indoor air quality (IAQ) research has benefited substantially from the development of low-cost monitors, which provide an opportunity to understand the dynamics of important indoor air pollutants at high spatial and temporal resolution. In particular, infrared CO2 sensors and optical particular counters (OPC) are ubiquitously deployed in various indoor environments and heating, ventilation, and air-conditioning (HVAC) systems. Indoor CO2 concentration is often considered a proxy for ventilation1 and IAQ and has been linked with inhalation exposure,2,3 cognitive tasks,4,5 and transmission of infectious disease,6,7 while particulate matter (PM) has known health consequences.8,9 However, although most low-cost IAQ sensors show acceptable relative precision, they often suffer from poor absolute accuracy and drift issues.10 These drawbacks severely limit the application of low-cost sensors in IAQ assessment, exposure monitoring, and building certification. Furthermore, the time series data of high temporal resolution from those sensors are often simply summarized as the integrated mean and standard deviation, without further analysis to extract useful information about building physics, occupant behavior, and their interactions.
Recently, data-driven tools have provided novel perspectives on how to take full advantage of data from low-cost air quality monitors. Machine learning techniques are increasingly used to predict building energy consumption,11−13 indoor environmental quality,14−17 occupant sensation,18−23 and airborne exposure.24−26 So far, the majority of relevant studies have focused on forecasting using time series analysis27 or neural network models.28,29 Further, the dynamics of indoor environmental parameters can be linked with building physics and occupant activities,30,31 yet understanding this complex link requires advanced data analysis tools. For example, Carrilho et al. developed a novel signal processing approach based on the covariation of indoor and outdoor CO2 concentration,32 which was then used by Alavy et al. to estimate the year-long time-resolved air change rate.33 Another recent study proposed an inverse modeling approach for estimating air change rate by searching for the air change rate that best explains the actual indoor CO2 concentration and relative humidity trends.34 These studies demonstrate the potential of using data-driven methods to understand building performance in general and air change rate in particular. However, the existing methods usually require prior knowledge about the environment and/or unmeasurable model parameters and thus work best for known contexts.35
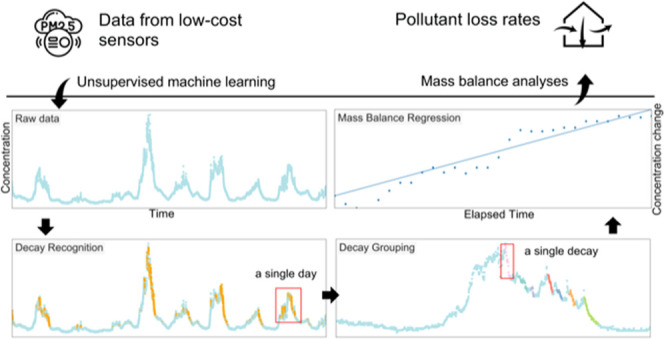
This paper proposes a novel unsupervised machine learning method that extracts useful fragments from continuous pollutant concentration time series data for calculating pollutant loss rates and estimating air change rate. The method only requires existing data from a single low-cost sensor. After automatically detecting emission and decay episodes from pollutant concentration curves, the proposed model calculates the loss rate using a mass balance equation (the same regression analysis as used in the tracer gas decay method36). However, different from traditional methods that require deliberate tracer gas release, the current method relies on inherent pollutant sources (e.g., building occupants as a source for metabolic CO2 and their indoor activities as a source for particles) to produce concentration elevations and estimate the effectiveness of loss mechanisms including ventilation, deposition, and filtration. When the strength of other loss mechanisms is negligible, e.g., in the case of CO2 in most indoor environments, the loss rate is a reasonable proxy for air change rate. Therefore, automatically recognizing those decay periods can achieve a long-term estimation of pollutant loss rate (and/or air change rate) with minimal effort at a temporal resolution of several estimates per day.
2. Methodology
2.1. Model Framework
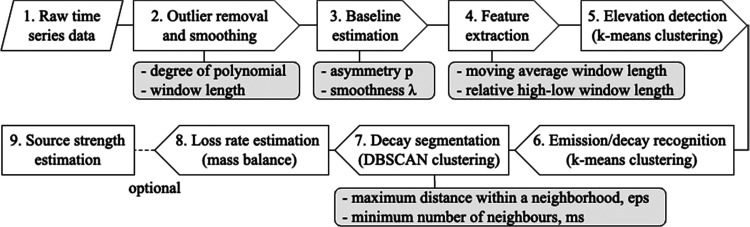
The proposed model automatically detects continuous drops in pollutant concentration data (referred to as decays) and uses the relevant portions of data to estimate the loss rate of pollutants of interest. Depending on the type of pollutants and the corresponding loss mechanisms in an indoor environment, the estimated loss rate can be linked with important building parameters such as air change rate and particle removal rates. The process is summarized in Figure 1, and an illustrative example of the key steps is shown in Figure S1 in the Supporting Information (SI).
Figure 1.
Block diagram of the decay recognition and loss rate estimation process (hyperparameters related to each step are shown in gray boxes if applicable).
The model requires minimal preprocessing of raw data. Depending on how noisy the raw data are, outlier removal and smoothing may help improve the signal-to-noise ratio by reducing the impact of extreme values and local random fluctuations. In the current study, we used the local outlier factor algorithm37 to detect and remove outliners and a Savitzky–Golay filter38 for smoothing. We then estimated the baseline concentration (the background indoor concentration without the presence of any source) before extracting data features for clustering. Different baseline detection algorithms were compared, and the Asymmetric Least Squares Smoothing (ALS)39 algorithm was chosen. The impact of baseline estimation is further discussed in the Results section.
Next, significant elevations in concentration are detected using a two-center k-means clustering algorithm (Figure 1.5). This clustering method is a widely used unsupervised learning technique that partitions data into a predefined number of clusters. The data features that show the highest clustering power were found to be: (1) the moving average of concentration after baseline removal c_map(t) (where p is the window length) and (2) the absolute value of concentration gradient after baseline removal c_gd_abs(t) defined as eq 1. As the distance between data samples is measured by Euclidean distance, it is necessary to perform data normalization to avoid exaggerating data features with relatively larger numeric values. A quantile transformer followed by a min-max scaler was used here.
| 1 |
The recognized elevations can be further categorized into emission, plateau, and decay periods using another three-center k-means clustering method (Figure 1.6). The data features used in this step are: (1) the positive or negative sign of the concentration gradient c_gd(t) and (2) the relative high–low position of the concentration at time t c_rhlq(t) that is defined as eq 2 (where c(t) is the concentration at time t after baseline removal and q is the window length of high–low comparison40). The second data feature accounts for the position of a single data point in relation to the moving minimum and maximum, so it captures an increasing or decreasing trend.
| 2 |
Data points recognized as decay are further segmented into individual decay events using the density-based spatial clustering of applications with noise (DBSCAN) based on daily concentration data (Figure 1.7). Unlike k-means clustering, DBSCAN automatically determines the number of cluster centers. With proper hyperparameters, this clustering method can select consistent long decay episodes while excluding short concentration fluctuations. The two data features used here are the time of the day and the sum of nondecay data points prior to the current data point (this sum will increase upon intervals between two decay groups but remain constant within a decay group). Further, using daily data instead of the whole dataset prevents the results from being dominated by occasional high concentrations.
The clustering results with regard to the selected data features for the office example are shown in Figures S2–S4 in the SI. Generally, decays can be well separated from the baseline and segmented into individual events. Finally, linear regression based on a well-mixed mass balance41 was conducted on each decay event to calculate the pollutant loss rate (Figure 1.8). When no indoor source is present, the concentration of a specific pollutant follows eq 3
| 3 |
where ct is the indoor pollutant concentration at timestamp t; c0 is the indoor pollutant concentration when decay starts; cout is the concentration of the same pollutant in air supply; L is the loss rate of a pollutant due to ventilation, deposition, and filtration, etc.; λ is the building air change rate; and t is the time lapse since decay starts. In an indoor environment, the makeup air can come from multiple sources in addition to the outdoors. Thus, in the current study, cout was replaced by the estimated baseline. Further, when the other loss mechanisms are negligible relative to ventilation (i.e., L ≈ λ), eq 3 can be rearranged as eq 4, and linear regression can be fit between ln [(ct – cout)/(c0 – cout)] and t to estimate air change rate λ (eq 5).
| 4 |
| 5 |
2.2. Hyperparameter Selection
The model hyperparameters involved in preprocessing and clustering are listed in Figure 1. The selection of hyperparameters affects clustering performance and consequently the estimated pollutant loss rates. In data preprocessing, the degree of smoothing polynomial and the window length are two important parameters. Proper smoothing helps increase the signal-to-noise ratio, but overly smoothing may cause data distortion and bias the loss rates. In general, we found a second-order polynomial with a window length of 3–9 is appropriate for data from low-cost CO2 and PM2.5 sensors with 1 min intervals, and PM2.5 data usually need more aggressive smoothing. Further, in baseline estimation, the ALS method takes two key parameters, namely, p for asymmetry and λ for smoothness. Within the recommended range (0.001 ≤ p ≤ 0.1, 102 ≤ λ ≤ 109), a combination of p = 0.001–0.01 and λ = 109 produced the best fitting for our datasets. However, those parameters should be adjusted according to the sampling interval as well as the characteristics of the environment and pollutant sources.
The window lengths for calculating the moving average and relative high–low position in feature extraction affect the performance of k-means clustering. A wider moving average window reduces the impact of local fluctuations but tends to misclassify data around the transition periods and can thus omit short elevations/decays. The relative high–low window controls which previous period to compare to in trend detection, and it should be selected according to the length of potential emission and decay periods. For DBSCAN, two hyperparameters determine the segmentation of individual decay events, namely, the maximum distance within a neighborhood and the minimum number of members in a neighborhood center. A larger distance will cluster data points that are not temporally adjacent (e.g., with a nondecay period in between) into the same group and thus bias the mass balance analysis. In contrast, a smaller distance can break a long decay period into several subsets, which results in repetitive decay rate estimations but has no major impact on the mean loss rate. The minimum sample number governs the keeping or discarding of small clusters and has a joint effect on the segmentation result. In general, we hope to avoid merging temporally disconnected data samples and keep as many valid decays as possible to characterize the temporal variation of pollutant loss rates.
We determined the optimal model hyperparameters using a grid search method (refer to Figures S5 and S6 in the SI). The performance matrice for k-means clustering includes the Calinski–Harabasz index42 and Davies–Bouldin index,43 which evaluate data separation, while the performance of DBSCAN is assessed by the number of decays extracted and their R2 value in mass balance regression. In addition, it is important to plot the concentration data with the recognized decay periods and visually inspect the results. The selected optimal clustering hyperparameters are summarized in Table 1 for the four environments. Also, we conducted a sensitivity analysis to investigate the impact of hyperparameters on the estimated loss rates using the office CO2 data as an example (Table S1 in the SI). Before result filtration, baseline estimation and DBSACN parameters have a large impact on the mean CO2 loss rate. However, after result filtration, only the maximum distance in DBSCAN has an impact of greater than 10% on the mean loss rate, and an unreasonable maximum distance value can be recognized by visually examining the decay recognition result.
Table 1. Summary of Selected Optimal Clustering Model Hyperparameters.
| k-means clustering |
DBSCAN |
|||
|---|---|---|---|---|
| dataset (sampling interval) | moving average window | relative high–low window | maximum distance | minimum samples |
| laboratory | ||||
| CO2 (1 min) | 5 | 5 | 0.01 | 10 |
| PM2.5 (15 s) | 10 | 10 | 0.01 | 20 |
| office | ||||
| CO2 (1 min) | 5 | 5 | 0.01 | 5 |
| PM2.5 (1 min) | 5 | 5 | 0.005 | 5 |
| classroom | ||||
| CO2 (1 min) | 3 | 5 | 0.005 | 10 |
| PM2.5 (15 s) | 10 | 20 | 0.005 | 20 |
| home | ||||
| CO2 (10 s) | 10 | 30 | 0.01 | 5 |
2.3. Result Filtration
Post-regression result filtration is another important step that improves the accuracy and reliability of the estimated pollutant loss rate. The model recognizes all consistent decay periods, but only some of them provide meaningful information about the environment. Extremely short or noisy decays should be excluded from loss rate estimations. We performed result filtration by setting thresholds for the duration of decays, the regression R2 value in mass balance analyses, and the concentration difference from the baseline so that only long, consistent, and predominant decays were kept. The appropriate thresholds were determined based on the number of remaining decays and their variability after thresholding (details are available in the SI and an example is provided based on the office data in Figures S7–S9).
The selected data filtration thresholds for the four datasets are summarized in Table 2. The laboratory environment had controlled artificial sources and known ventilation rates. Only a duration threshold of 30 min was used to remove short decays outside the actual experiment hours due to experiment preparation and data collection. The office had a maximum occupancy of three and was mostly used by one person during the measurement period. Therefore, the data show clear elevations and decays, and less strict thresholds are needed. In contrast, the classroom had a maximum occupancy of 80. A longer duration threshold and a higher concentration difference threshold were selected to potentially exclude the short breaks between classes when a few students left the room while others remained inside (the CO2 loss rate at those moments is not a proxy for air change rate as sources are still present). For the residential dataset, relatively stricter thresholds were applied to increase the reliability of air change rate estimation. Still, on average, more than two decays per day are available for characterizing the daily and seasonal variations.
Table 2. Summary of Selected Duration, r-Squared, and Concentration Difference Thresholds for Result Filtration.
| dataset | duration threshold (min) | R2 threshold | concentration difference threshold |
|---|---|---|---|
| laboratory | 30 | ||
| office | 5 | 0.7 | 25 ppm & 5 μg/m3 |
| classroom | 15 | 0.6 | 50 ppm & 1 μg/m3 |
| home (CO2 only) | 30 | 100 ppm |
2.4. Data Sources
The model was first established using data from a controlled environmental chamber and then applied to three environments (an office, a classroom, and a home) to explore the impact of sensor consistency, occupancy, air mixing, and baseline estimation on the estimated pollutant loss rates. The laboratory chamber is equipped with a mechanical ventilation system. During the tests, the supply and return air volumes were individually controlled, while artificial sources were used to elevate the indoor CO2 and PM concentrations (metabolic CO2 from two researchers and a used dust bag from a vacuum cleaner, respectively). The tests aimed to validate the accuracy and reliability of the decay recognition method by comparing the estimated pollutant loss rates with the measured equivalent air change rate. For real-world scenarios, the office is a graduate student office with six desks (maximum occupancy of three due to COVID-19 regulations). Five CO2 sensors and six particle counters were collocated on one of the desks to investigate the sensor consistency and explore the impact of pollutant baseline estimation. The classroom is significantly larger with a higher occupancy density when in use (maximum occupancy 80). CO2 and PM2.5 concentrations were monitored at three locations to capture the spatial variation of pollutant loss rates. The home is a semidetached house in Toronto where long-term CO2 monitoring was conducted in the living room for approximately a year. Alavy et al.33 have previously estimated the long-term air change rate of this house using a signal processing approach, which was compared to the estimated CO2 decay rate from the current model. Details about each environment and the corresponding data are summarized in Table 3.
Table 3. Summary of the Monitoring Environments and the Corresponding Datasets.
| environment | dimensions (L × W × H) | sensor | monitoring locations | duration | purpose |
|---|---|---|---|---|---|
| laboratory | 3.5 × 2.7 × 3 m | CO2 (AirMaster AM6) | center, return | 30 h | validation, model development |
| PM2.5 (Alphasense N2) | |||||
| office | 4 × 3.5 × 3 m | CO2 (Senseair K30) | collocated on a desk | 8 days | collocation, baseline selection |
| PM2.5 (Dylos DC1700) | |||||
| classroom | 15 × 7 × 2.7 m | CO2 (PP systems SBA-5) | podium, front, back | 11 days | air mixing, varying occupancy |
| PM2.5 (Alphasense N2) | |||||
| residential | 185 m2, three-story | CO2 (PP systems SBA-5) | living room | 1 year | comparison with another method |
3. Results
This section shows the decay rate estimation results from the four environments based on optimized model hyperparameters after result filtration. The loss rates of CO2 and PM2.5 in the same environment are compared where applicable. In most indoor environments, occupants are the single source of CO2 and ventilation is the only loss mechanism. Therefore, the CO2 loss rate is considered a proxy for air change rate. In contrast, particles are subject to deposition and sometimes filtration, so the PM2.5 loss rate indicates the total sum of all particle removal processes (ventilation, deposition, and filtration).
3.1. Environmental Chamber Data
The daily CO2 and PM2.5 concentration curves in the environmental chamber at the center location are shown in Figure S10 (recognized decays are differentiated by colors). The elevations are predominant (approximately 400 ppm and 40 μg/m3 above the baseline), each lasting for about an hour.
Two ventilation conditions were tested. Under the first condition, the supply and return air flow rates as well as the outdoor air flow rates were all set to 5/h equivalent; under the second condition, the supply and return rates were 2.5/h equivalent while the outdoor air rate was approximately 1.2/h. The system has a HEPA filter installed and the outdoor PM2.5 concentration is generally low near the laboratory, so the air supply can be considered PM-free. The estimated CO2 and PM2.5 loss rates at the two monitoring locations (at the center of the room and near air return) after result filtration are compared to the outdoor air change rate (outdoor flow rate divided by room volume) and equivalent air change rate (return flow rate divided by room volume) reported by the HVAC control system in Figure 2. It is found that the estimated CO2 and PM2.5 loss rates at the room center and near return are consistent. The PM2.5 loss rate agrees well with the measured equivalent air change rate under both conditions. The estimated CO2 loss rate is very similar to the measured outdoor air change rate under the low ventilation condition (2.5/h equivalent air change rate and 1.2/h outdoor air change rate) but significantly lower than the measured value under the high ventilation condition (5/h air change rate). This difference was likely due to that the air supply contained some return air rather than all outdoor air. A schematic of the system is shown in Figure S11. Although the supply, return, and outdoor flow rates can be independently controlled, the opening of return and bypass dampers were automatically determined. In the 5 ACH condition, the return damper was likely not fully closed and a fraction of return air could have been mixed into supply.
Figure 2.
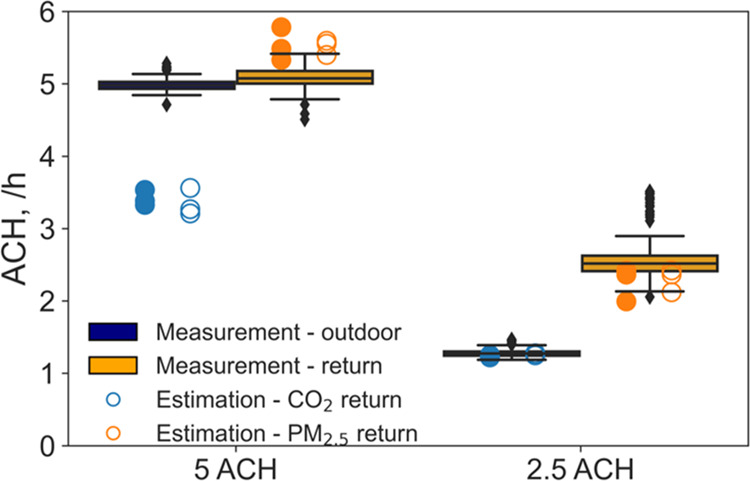
Comparison between estimated decay rates and measured air change rates in the environmental chamber (ACH = air changes per hour, solid circles = at center, hollow circles = near return).
3.2. Office Data
The daily concentration curves on a single day from single CO2 and PM2.5 sensors are shown in Figure S12 with the recognized decays individually colored. The concentration data in the office are noisier than those in a controlled chamber. PM2.5 concentration was measured as a number concentration but converted to a mass concentration assuming a density of 1 g/cm3 (note that the assumed density does not impact decay rates). The duration of decays varied from approximately 30 min to 2 h (except for very short decays that were excluded). Also, the PM2.5 data are significantly noisier, making the concentration curve a wide band, which resulted in a lower r-squared value in the mass balance regression analyses.
After result filtration, 236 and 198 decays (approximately 5 and 4 decays per sensor per day) remain for CO2 and PM2.5 data, respectively. The cumulative frequency of the estimated decay rates of CO2 and PM2.5 after result filtration is shown in Figure 3. The CO2 decay rate is estimated to have a median of 0.83/h and mostly ranges within 0.5–1.5/h. In contrast, PM2.5 has a higher decay rate (p = 0.001, Wilcoxon rank sum test) with a median of 1.31/h and a comparatively wider distribution. The estimated decay rate of PM2.5 is greater than that of CO2 presumably because, in this environment, ventilation is the only loss mechanism for CO2 while PM2.5 is also subject to deposition, and the difference of approximately 0.5/h is consistent with the PM2.5 deposition loss rate reported in the literature.44,45 However, these results should not be taken as a paired comparison between the loss rates of CO2 and PM2.5, as decays can happen at different times.
Figure 3.
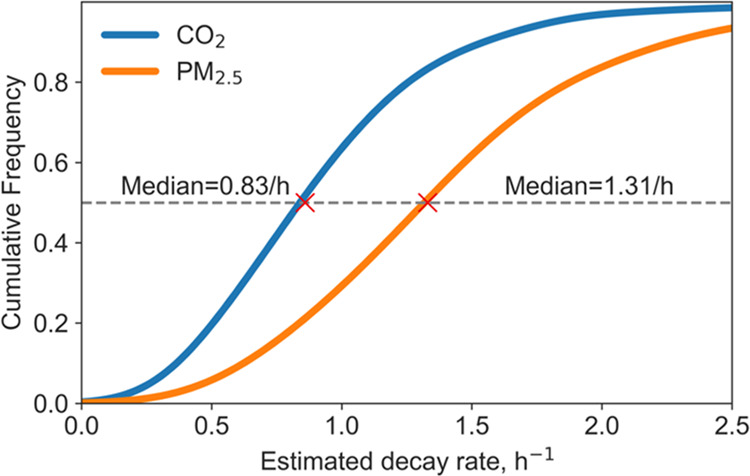
Cumulative frequency of estimated decay rates in the office (after result filtration).
With 5–6 sensors collocated for one week, this dataset was also used to explore the influences of baseline selection and sensor consistency. Figure 4 shows two different baseline estimation methods and the corresponding estimated loss rate of PM2.5. In an indoor space, the concentration decrease rate of a pollutant is decided by both the fresh air supply rate and the concentration of the same pollutant in the makeup air. Therefore, based on the same concentration curve, the higher the baseline concentration is, the smaller the difference between indoor and outdoor concentration will be, and thus a higher air change rate is needed to cause the same decay. In this study, we compared two methods for estimating the baseline, namely, the simple estimation that takes the daily median concentration of the nonelevated periods as the baseline, and the ALS39 algorithm, a smoother one with an asymmetric weighting of deviations. It is found that the simple estimation produces a consistently higher estimated baseline and consequently a slightly higher estimated decay rate of PM2.5 on average. The diurnal and daily variations of the decay rate are also higher, presumably because using a fixed baseline value throughout a day could cause frequent overestimations and underestimations of the pollutant concentration in the incoming air and thus higher uncertainties. In comparison, the ALS method attempts to capture the diurnal variation of the baseline concentration based on local minimum values. Similar results are found with the office CO2 data (Figure S13 in the SI). Therefore, ALS is selected as the baseline estimation algorithm in this paper. It is also possible to use outdoor data as the baseline. However, there are two major limitations: air exchange can happen between different indoor spaces so the outdoor concentration may not represent the concentration in the replacing air; the between-instrument variation is often large for low-cost sensors so the indoor/outdoor difference can partially result from instrument variation.
Figure 4.
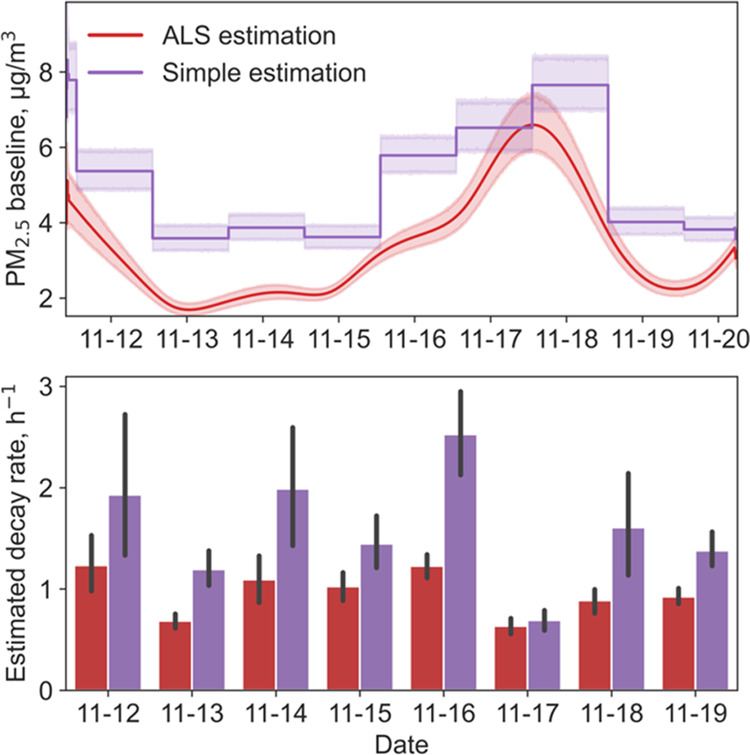
(Top) Different PM2.5 baseline estimates (the band shows the standard deviation across six different sensors) and (bottom) the corresponding estimated decay rate in the office.
As we aim to develop an accessible data-driven method that utilizes data from low-cost sensors, it is important whether sensor sample variation impacts the results. Figure 5 shows the PM2.5 concentration data from six collocated Alphasense N2 OPC monitors for eight consecutive days and the corresponding estimated PM2.5 loss rate. The diurnal variations of PM2.5 concentration captured by the six sensors match well, although Sensor 5 constantly reported a slightly higher concentration. Despite the discrepancy in concentration, the estimated decay rate coincides well across all sensors (p = 0.98, one-way ANOVA test) after result filtration based on duration and r-squared thresholds. The CO2 concentration data measured by five collocated Senseair K30 sensors during the same period are shown in Figure S14, where the corresponding decay rate estimates are also consistent across sensors (p = 0.97, one-way ANOVA test). These results suggest that the proposed decay recognition and decay rate estimation method has a high tolerance for some raw data quality issues and works well with the tested low-cost air quality monitors.
Figure 5.
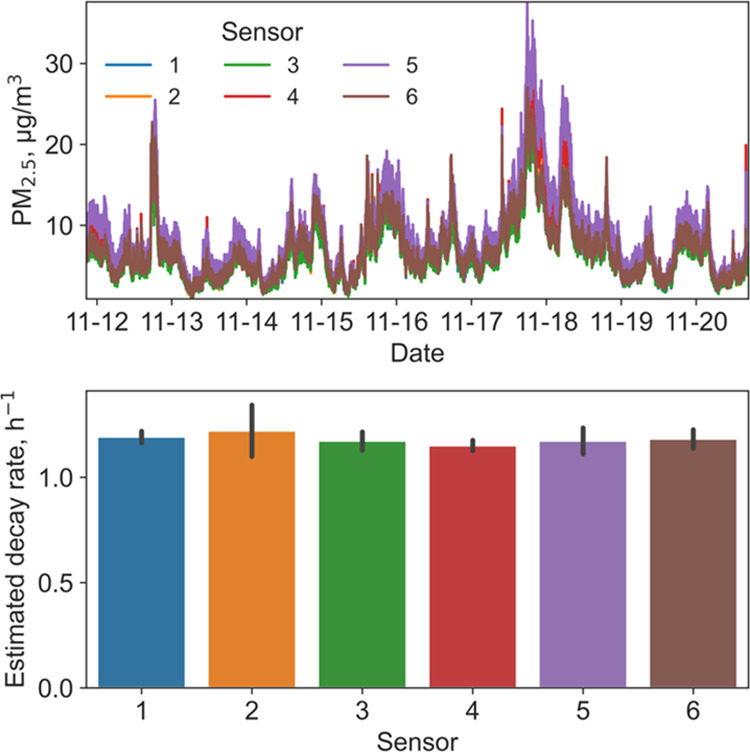
(Top) PM2.5 concentration data from six collocated low-cost CO2 sensors and (bottom) the corresponding estimated decay rates in the office.
3.3. Classroom Data
We further tested the generalizability of the model using data collected from a classroom (the CO2 and PM2.5 concentration data on a single day are shown in Figure S15). The cumulative frequency of the predicted decay rate of CO2 and PM2.5 at different locations after result filtration is shown in Figure 6 (PM2.5 data not available at the podium because of power failure). The decay rate of CO2 was significantly higher at the podium (dotted blue line) with a median of 3.10/h compared to that at the front and back locations (p < 0.001, independent t-test after logarithmic transformation). This difference is presumably due to the mechanical ventilation system with two outlets and an inlet above the blackboard causing an air flow short circuit (a photo is shown in Figure S16). Such a result highlights the potential applications of the proposed model for capturing the long-term air-mixing conditions within an indoor environment, but it also shows the limitation of using the model to evaluate the air change rate of a large space based on CO2 decay rate as the model output is the local loss rate at the sensor location. To characterize the whole-room ventilation condition, multiple sensors at different locations are needed. The estimated PM2.5 decay rate was significantly higher than that of CO2 at the same location (p < 0.01, independent t-test after logarithmic transformation) with a median of 2.26–2.38/h. The pollutant loss rates in the classroom were high because the university enhanced classroom ventilation during the COVID-19 pandemic through a combination of outdoor air ventilation, central ventilation, and HEPA air filtration.46
Figure 6.
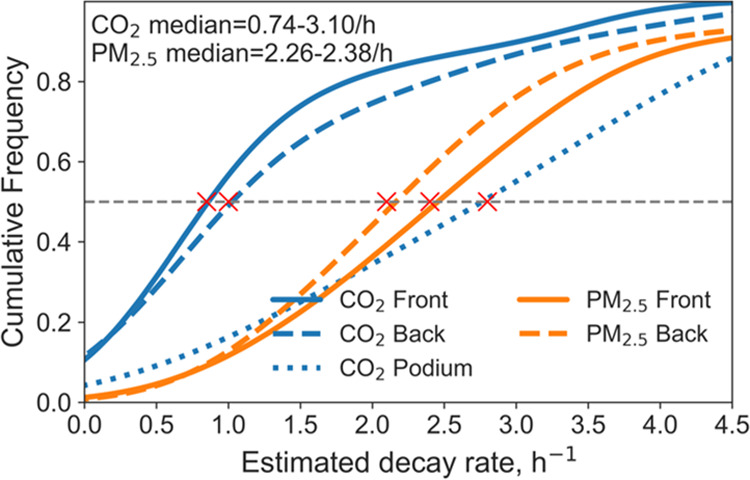
Cumulative frequency of estimated decay rates at different locations in the classroom (after result filtration).
3.4. Residential Data
The CO2 concentration data from the semidetached house have less noise than the office or school (daily example shown in Figure S17). The major elevations of indoor concentration were caused by building occupants entering the room, and the following decays usually lasted 2–3 h. After result filtration, approximately two decays remain on average per day, with a median loss rate of 0.45/h. The estimated daily average air change rate fluctuated between 0.25 and 0.75/h throughout winter and transition seasons but increased considerably in summer, reaching 2–3/h (Figure S18). This seasonal difference was likely caused by window opening in the summer.
A previous study has estimated the air change rate of the house using a different data-driven method.33 The method uses signal processing techniques and estimates the air change rate according to the covariation of the indoor and outdoor CO2 concentrations. A major advantage of the signal processing method is the high temporal resolution of air change rate estimation, often the same as the CO2 sampling frequency. However, it requires simultaneous monitoring of the outdoor data and thus cannot be applied to existing datasets containing only indoor measurements. There are also substantial challenges around the selection of filter parameters used in the signal processing approach. The cumulative frequency of the estimated air change rate using the two methods is compared in Figure 7. As is shown, the median air change rate is similar between the two methods but the frequency distribution is considerably different (p < 0.001, Wilcoxon rank sum test). The automatic decay recognition method proposed in this study produced estimated air change rates that are approximately normally distributed, with the majority between 0.2 and 0.7/h. In contrast, the estimates from the signal processing method are more evenly distributed in the range of 0–2/h. The signal processing approach shows a wider spread because the constantly fluctuating indoor and outdoor CO2 concentrations can result in varying air change rates within short periods. In contrast, the automatic decay recognition method produces only a few estimates per day, presumably at similar times of day depending on the routine of the building occupants, which is more likely to capture air change rates in a narrower range. It is also notable that the current decay recognition method estimated a higher air change rate during summer months when windows were more likely to be kept open, while the signal processing method shows an opposite trend.
Figure 7.
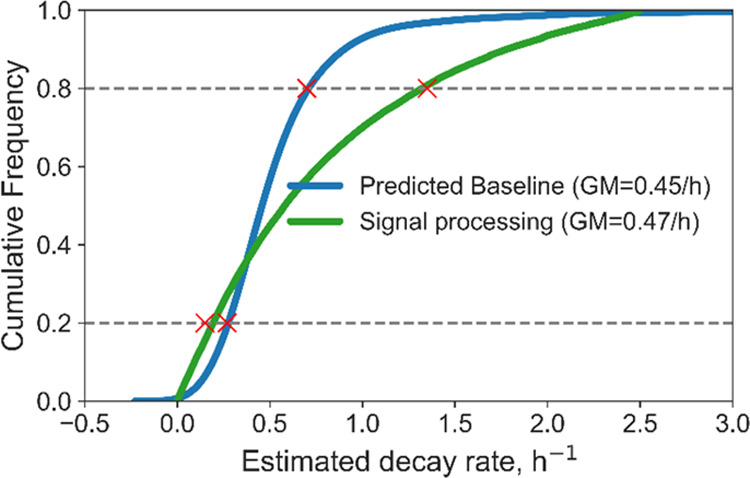
Comparison between the signal processing method and the proposed decay recognition method in the home.
4. Discussion
The proposed model based on unsupervised clustering is able to extract decay periods from CO2 and PM2.5 concentration data and estimate their decay rates whenever a decay is found. In most environments, the decay rate of CO2 is a proxy for air change rate and can be used to evaluate building ventilation. In comparison, the decay rate of PM2.5 includes ventilation, deposition, and filtration loss mechanisms and indicates the effectiveness of particle removal strategies. In the context of the COVID-19 pandemic, the results also facilitate understanding the indoor airborne transmission of infectious diseases.
The model showed reliable performance on multiple datasets collected from different types of buildings. Also, reproducible and easy-to-follow protocols were developed to select optimal model hyperparameters and filter undesired results. Visual inspection and comparison to deliberate emission tests confirmed that the recognized decays were consistent with those that human experts would have chosen and the estimated decay rates were reasonable. Further, the model worked well on both CO2 and PM2.5 time series. When applied to CO2 data, it makes no assumption about the metabolic CO2 emission rate and thus is not subject to the uncertainties caused by variations of CO2 emission across gender, age, physiology, and activity level.47 Also, this method takes data input from only one sensor and relies on the (relative) precision rather than (absolute) accuracy of the sensor, making it highly compatible with the use of low-cost air quality monitors. Further, since emission episodes are recognized along with decays, future studies may use this model to characterize the in situ emission rate of various indoor air pollution sources. Compared to simple rules for determining emission and decay events based on consecutive concentration changes (which also require sophisticated data filtering and preprocessing), the current method and its hyperparameter selection have better generalizability. As opposed to the neural network and deep learning methods that are increasingly used for similar peak/elevation detection in spectrometry data,48,49 our unsupervised clustering-based model is less computationally expensive and easier to understand.
After decay periods are recognized, decay rate estimation is based on the mass balance equation. A few limitations exist in this process. For CO2, as the indoor concentration is often of the same order of magnitude as that outdoors, the baseline concentration in the makeup air has a large impact on its dilution potential and consequently the estimated loss rate. The baseline can be estimated using various simple or advanced algorithms, but uncertainty in this process is difficult to quantify especially when cross-ventilation between adjacent indoor environments is present. The same limitation also applies to particles when no strong indoor particle source is present. Although the lack of knowledge of the baseline concentration is a limitation for applications on existing data, new research projects can overcome this limitation by conducting deliberate periodical release of high-concentration tracer gas or particles (e.g., at the end of each day). Further, loss rates are calculated assuming no active indoor source during the decay period. A coincidental source may interrupt the decay and increase uncertainty in the result. For example, CO2 decays may be recognized when only a fraction of building users leave the space. Such uncertainty can be partially regulated by proper result filtration (i.e., excluding short decays with low regression r-squared value) and addressed by adding an occupancy sensor. However, this method should not be applied to indoor environments containing a known continuous PM or CO2 source. Besides, there is potential sampling bias if occupancy follows a fixed routine. Then, the results represent pollutant decay rates at similar times of the day and may not capture the intraday variability well.
Acknowledgments
The authors thank Prof. Greg Evans, Nishitha Shashidhar, and Taylor Edwards for sharing the outdoor CO2 concentration data. They are grateful to Prof. Seungjae Lee for advising on the evaluation of unsupervised learning models. This research was supported by Natural Sciences and Engineering Research Council of Canada (RGPIN-2022-04325) and the Canada Foundation for Innovation (32319) and Ontario Research Fund (3660). B.D. received financial support from the Ontario Trillium Scholarship.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.3c00756.
Visualization of clustering results, details about hyperparameter selection and data filtration approaches, schematic of the HVAC system for the laboratory chamber, and example of sensitivity analysis for hyperparameter selection (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Morse R. G.; Haas P.; Lattanzio S. M.; Zehnter D.; Divine M. A cross-sectional study of schools for compliance to ventilation rate requirements. J. Chem. Health Saf. 2009, 16, 4–10. 10.1016/j.jchas.2009.02.001. [DOI] [Google Scholar]
- Zhang D.; Bluyssen P. M.. Exploring the possibility of using CO2 as a proxy for exhaled particles to predict the risk of indoor exposure to pathogens Indoor Built Environ. Published online June 27, 2022, 10.1177/1420326X221110043. [DOI]
- Rivas E.; Santiago J. L.; Martín F.; Martilli A. Impact of natural ventilation on exposure to SARS-CoV 2 in indoor/semi-indoor terraces using CO2 concentrations as a proxy. J. Build. Eng. 2022, 46, 103725 10.1016/J.JOBE.2021.103725. [DOI] [Google Scholar]
- Du B.; Tandoc M. C.; Mack M. L.; Siegel J. A. Indoor CO2 concentrations and cognitive function: A critical review. Indoor Air. 2020, 30, 1067–1082. 10.1111/INA.12706. [DOI] [PubMed] [Google Scholar]
- Allen J. G.; MacNaughton P.; Satish U.; Santanam S.; Vallarino J.; Spengler J. D. Associations of Cognitive Function Scores with Carbon Dioxide, Ventilation, and Volatile Organic Compound Exposures in Office Workers: A Controlled Exposure Study of Green and Conventional Office Environments. Environ. Health Perspect. 2016, 124, 805–812. 10.1289/ehp.1510037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Z.; Jimenez J. L. Exhaled CO2 as a COVID-19 infection risk proxy for different indoor environments and activities. Environ. Sci. Technol. Lett. 2021, 8, 392–397. 10.1021/acs.estlett.1c00183. [DOI] [PubMed] [Google Scholar]
- Baselga M.; Alba J. J.; Schuhmacher A. J. The Control of Metabolic CO2 in Public Transport as a Strategy to Reduce the Transmission of Respiratory Infectious Diseases. Int. J. Environ. Res. Public Health 2022, 19, 6605. 10.3390/ijerph19116605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y.; Zhang Y.; Chen C.; Sun Q.; Wang Y.; Du H.; Wang J.; Zhong Y.; Shi W.; Li T.; Shi X. Impact of Heavy PM2.5 Pollution Events on Mortality in 250 Chinese Counties. Environ. Sci. Technol. 2022, 56, 8299–8307. 10.1021/acs.est.1c07340. [DOI] [PubMed] [Google Scholar]
- Hu Y.; Ji J. S.; Zhao B. Deaths Attributable to Indoor PM2.5 in Urban China When Outdoor Air Meets 2021 WHO Air Quality Guidelines. Environ Sci Technol. 2022, 56, 15882–15891. 10.1021/ACS.EST.2C03715. [DOI] [PubMed] [Google Scholar]
- Williams D. E. Low Cost Sensor Networks: How Do We Know the Data Are Reliable?. ACS Sens. 2019, 4, 2558–2565. 10.1021/acssensors.9b01455. [DOI] [PubMed] [Google Scholar]
- Ahmad T.; Chen H.; Huang R.; Yabin G.; Wang J.; Shair J.; Akram H. M.; Mohsan S. A.; Kazim M. Supervised based machine learning models for short, medium and long-term energy prediction in distinct building environment. Energy 2018, 158, 17–32. 10.1016/J.ENERGY.2018.05.169. [DOI] [Google Scholar]
- Tsanas A.; Xifara A. Accurate quantitative estimation of energy performance of residential buildings using statistical machine learning tools. Energy Build. 2012, 49, 560–567. 10.1016/J.ENBUILD.2012.03.003. [DOI] [Google Scholar]
- Edwards R. E.; New J.; Parker L. E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. 10.1016/J.ENBUILD.2012.03.010. [DOI] [Google Scholar]
- Kallio J.; Tervonen J.; Räsänen P.; Mäkynen R.; Koivusaari J.; Peltola J. Forecasting office indoor CO2 concentration using machine learning with a one-year dataset. Build. Environ. 2021, 187, 107409 10.1016/J.BUILDENV.2020.107409. [DOI] [Google Scholar]
- Seo J.; Choi A.; Sung M. Recommendation of indoor luminous environment for occupants using big data analysis based on machine learning. Build. Environ. 2021, 198, 107835 10.1016/J.BUILDENV.2021.107835. [DOI] [Google Scholar]
- Wei W.; Ramalho O.; Malingre L.; Sivanantham S.; Little J. C.; Mandin C. Machine learning and statistical models for predicting indoor air quality. Indoor Air. 2019, 29, 704–726. 10.1111/INA.12580. [DOI] [PubMed] [Google Scholar]
- Thomas B.; Soleimani-Mohseni M. Artificial neural network models for indoor temperature prediction: Investigations in two buildings. Neural Comput. Appl. 2006, 16, 81–89. 10.1007/s00521-006-0047-9. [DOI] [Google Scholar]
- Luo M.; Xie J.; Yan Y.; Ke Z.; Yu P.; Wang Z.; Zhang J. Comparing machine learning algorithms in predicting thermal sensation using ASHRAE Comfort Database II. Energy Build. 2020, 210, 109776 10.1016/J.ENBUILD.2020.109776. [DOI] [Google Scholar]
- Kim J.; Zhou Y.; Schiavon S.; Raftery P.; Brager G. Personal comfort models: Predicting individuals’ thermal preference using occupant heating and cooling behavior and machine learning. Build. Environ. 2018, 129, 96–106. 10.1016/J.BUILDENV.2017.12.011. [DOI] [Google Scholar]
- Cosma A. C.; Simha R. Machine learning method for real-time non-invasive prediction of individual thermal preference in transient conditions. Build. Environ. 2019, 148, 372–383. 10.1016/J.BUILDENV.2018.11.017. [DOI] [Google Scholar]
- Wang Z.; Yu H.; Luo M.; Wang Z.; Zhang H.; Jiao Y. Predicting older people’s thermal sensation in building environment through a machine learning approach: Modelling, interpretation, and application. Build. Environ. 2019, 161, 106231 10.1016/J.BUILDENV.2019.106231. [DOI] [Google Scholar]
- Fan L.; Ding Y. Research on risk scorecard of sick building syndrome based on machine learning. Build. Environ. 2022, 211, 108710 10.1016/J.BUILDENV.2021.108710. [DOI] [Google Scholar]
- Sofuoglu S. C. Application of artificial neural networks to predict prevalence of building-related symptoms in office buildings. Build. Environ. 2008, 43, 1121–1126. 10.1016/J.BUILDENV.2007.03.003. [DOI] [Google Scholar]
- Mohammadshirazi A.; Kalkhorani V. A.; Humes J.; Speno B.; Rike J.; Ramnath R.; Clark J. D. Predicting airborne pollutant concentrations and events in a commercial building using low-cost pollutant sensors and machine learning: A case study. Build. Environ. 2022, 213, 108833 10.1016/J.BUILDENV.2022.108833. [DOI] [Google Scholar]
- Khazaei B.; Shiehbeigi A.; Haji Molla Ali Kani A. R. Modeling indoor air carbon dioxide concentration using artificial neural network. Int. J. Environ. Sci. Technol. 2019, 16, 729–736. 10.1007/s13762-018-1642-x. [DOI] [Google Scholar]
- Elbayoumi M.; Ramli N. A.; Yusof N. F. F. M. Development and comparison of regression models and feedforward backpropagation neural network models to predict seasonal indoor PM2.5–10 and PM2.5 concentrations in naturally ventilated schools. Atmos. Pollut. Res. 2015, 6, 1013–1023. 10.1016/J.APR.2015.09.001. [DOI] [Google Scholar]
- Deb C.; Zhang F.; Yang J.; Lee S. E.; Shah K. W. A review on time series forecasting techniques for building energy consumption. Renewable Sustainable Energy Rev. 2017, 74, 902–924. 10.1016/J.RSER.2017.02.085. [DOI] [Google Scholar]
- Challoner A.; Pilla F.; Gill L. Prediction of Indoor Air Exposure from Outdoor Air Quality Using an Artificial Neural Network Model for Inner City Commercial Buildings. Int. J. Environ. Res. Public Health 2015, 12, 15233–15253. 10.3390/IJERPH121214975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagesse B.; Wang S.; Larson Tv.; Kim A. A. Predicting PM2.5 in Well-Mixed Indoor Air for a Large Office Building Using Regression and Artificial Neural Network Models. Environ. Sci. Technol. 2020, 54, 15320–15328. 10.1021/acs.est.0c02549. [DOI] [PubMed] [Google Scholar]
- Morawska L.; Mengersen K.; Wang H.; Tayphasavanh F.; Darasavong K.; Holmes N. S. Pollutant concentrations within households in Lao PDR and association with housing characteristics and occupants’ activities. Environ. Sci. Technol. 2011, 45, 882–889. 10.1021/es102294v. [DOI] [PubMed] [Google Scholar]
- Huangfu Y.; Lima N. M.; O’Keeffe P. T.; Kirk W. M.; Lamb B. K.; Walden V. P.; Jobson B. T. Whole-House Emission Rates and Loss Coefficients of Formaldehyde and Other Volatile Organic Compounds as a Function of the Air Change Rate. Environ. Sci. Technol. 2020, 54, 2143–2151. 10.1021/acs.est.9b05594. [DOI] [PubMed] [Google Scholar]
- Dias Carrilho J.; Mateus M.; Batterman S.; Gameiro Da Silva M. Air exchange rates from atmospheric CO2 daily cycle. Energy Build. 2015, 92, 188. 10.1016/J.ENBUILD.2015.01.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alavy M.; Li T.; Siegel J. A. Exploration of a long-term measurement approach for air change rate. Build. Environ. 2018, 144, 474–481. 10.1016/J.BUILDENV.2018.08.051. [DOI] [Google Scholar]
- Xiong Z.; Berquist J.; Gunay H. B.; Cruickshank C. A. An inquiry into the use of indoor CO2 and humidity ratio trend data with inverse modelling to estimate air infiltration. Build. Environ. 2021, 206, 108365 10.1016/J.BUILDENV.2021.108365. [DOI] [Google Scholar]
- Liu X.; Lu D.; Zhang A.; Liu Q.; Jiang G. Data-Driven Machine Learning in Environmental Pollution: Gains and Problems. Environ. Sci. Technol. 2022, 56, 2124–2133. 10.1021/acs.est.1c06157. [DOI] [PubMed] [Google Scholar]
- Okuyama H.; Onishi Y. Uncertainty analysis and optimum concentration decay term for air exchange rate measurements: Estimation methods for effective volume and infiltration rate. Build. Environ. 2012, 49, 182–192. 10.1016/J.BUILDENV.2011.09.018. [DOI] [Google Scholar]
- Breunig M. M.; Kriegel H. P.; Ng R. T.; Sander J. In LOF: Identifying Density-Based Local Outlier, Proceedings of the 2000 ACM SIGMOD international conference on Management of data - SIGMOD ’00. Published online, 2000; pp 93–104 10.1145/342009.335388. [DOI]
- Savitzky A.; Golay M. J. E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1951, 36, 1627–1639. [Google Scholar]
- Baek S. J.; Park A.; Ahn Y. J.; Choo J. Baseline correction using asymmetrically reweighted penalized least squares smoothing. Analyst 2015, 140, 250–257. 10.1039/C4AN01061B. [DOI] [PubMed] [Google Scholar]
- Anghinoni L.; Zhao L.; Ji D.; Pan H. Time series trend detection and forecasting using complex network topology analysis. Neural Networks 2019, 117, 295–306. 10.1016/J.NEUNET.2019.05.018. [DOI] [PubMed] [Google Scholar]
- Alzona J.; Cohen B. L.; Rudolph H.; Jow H. N.; Frohliger J. O. Indoor-outdoor relationships for airborne particulate matter of outdoor origin. Atmos. Environ. (1967) 1979, 13, 55–60. 10.1016/0004-6981(79)90244-0. [DOI] [Google Scholar]
- Caliñski T.; Harabasz J. A Dendrite Method Foe Cluster Analysis. Commun. Statist. 1974, 3, 1–27. 10.1080/03610927408827101. [DOI] [Google Scholar]
- Halkidi M.; Batistakis Y.; Vazirgiannis M. Clustering validity checking methods. ACM SIGMOD Record 2002, 31, 19–27. 10.1145/601858.601862. [DOI] [Google Scholar]
- He C.; Morawska L.; Gilbert D. Particle deposition rates in residential houses. Atmos. Environ. 2005, 39, 3891–3899. 10.1016/J.ATMOSENV.2005.03.016. [DOI] [Google Scholar]
- Riley W. J.; McKone T. E.; Lai A. C. K.; Nazaroff W. W. Indoor Particulate Matter of Outdoor Origin: Importance of Size-Dependent Removal Mechanisms. Environ. Sci. Technol. 2002, 36, 200–207. 10.1021/ES010723Y. [DOI] [PubMed] [Google Scholar]
- Facilities & Services, University of Toronto. COVID-19 HVAC strategy. https://www.fs.utoronto.ca/services/hvac-mechanical-utilities/covid-hvac-strategy/. Accessed: August 11, 2022.
- Batterman S. Review and Extension of CO2-Based Methods to Determine Ventilation Rates with Application to School Classrooms. Int. J. Environ. Res. Public Health 2017, 14, 145. 10.3390/IJERPH14020145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell S.; Nazarov E.; Wang Y. F.; Rodriguez J. E.; Eiceman G. A. Neural Network Recognition of Chemical Class Information in Mobility Spectra Obtained at High Temperatures. Anal. Chem. 2000, 72, 1192–1198. 10.1021/AC991019R. [DOI] [PubMed] [Google Scholar]
- Melnikov A. D.; Tsentalovich Y. P.; Yanshole V. V. Deep Learning for the Precise Peak Detection in High-Resolution LC-MS Data. Anal. Chem. 2020, 92, 588–592. 10.1021/acs.analchem.9b04811. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.