Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jun 16;19(13):3982–3995. doi: 10.1021/acs.jctc.3c00363

Vertical Ionization Potentials and Electron Affinities at the Double-Hybrid Density Functional Level

Dávid Mester †,‡,¶,*, Mihály Kállay †,‡,¶,*
PMCID: PMC10339736  PMID: 37326360

Abstract

graphic file with name ct3c00363_0007.jpg

The double-hybrid (DH) time-dependent density functional theory is extended to vertical ionization potentials (VIPs) and electron affinities (VEAs). Utilizing the density fitting approximation, efficient implementations are presented for the genuine DH ansatz relying on the perturbative second-order correction, while an iterative analogue is also elaborated using our second-order algebraic-diagrammatic construction [ADC(2)]-based DH approach. The favorable computational requirements of the present schemes are discussed in detail. The performance of the recently proposed spin-component-scaled and spin-opposite-scaled (SOS) range-separated (RS) and long-range corrected (LC) DH functionals is comprehensively assessed, while popular hybrid and global DH approaches are also discussed. For the benchmark calculations, up-to-date test sets are selected with high-level coupled-cluster references. Our results show that the ADC(2)-based SOS-RS-PBE-P86 approach is the most accurate and robust functional. This method consistently outperforms the excellent SOS-ADC(2) approach for VIPs, although the results are somewhat less satisfactory for VEAs. Among the genuine DH functionals, the SOS-ωPBEPP86 approach is also recommended for describing ionization processes, but its performance is even less reliable for electron-attached states. In addition, surprisingly good results are attained by the LC hybrid ωB97X-D functional, where the corresponding occupied (unoccupied) orbital energies are retrieved as VIPs (VEAs) within the present formalism.

1. Introduction

Vertical ionization potentials (VIPs) and electron affinities (VEAs) are crucial parameters that are used to characterize the electronic structure of molecular systems. The accurate prediction of VIPs, for example, can provide insights into the properties of semiconducting materials used in solar cell devices. Therefore, understanding the relationship between VIPs and photovoltaic efficiency is of great importance in the development of next-generation solar cells.1−3 Furthermore, ionizing radiations can cause damage to DNA, with secondary electron attachment resulting in various forms of DNA degradation, making it important to understand the role of electron-attached states in genetics, biochemistry, and health sciences.4−10 The reliable prediction of these parameters for extended molecular systems is still a challenging task that requires accurate and efficient theoretical methods.

To obtain the total energy of a given system, the most commonly used approaches are based on the cost-effective density functional theory (DFT).11 Within DFT, the highest occupied Kohn–Sham (KS) orbital energy of an n-electron system can also be interpreted as the negative of the exact ionization potential;12−14 however, these values are often underestimated in comparison with the experimental results.12,15 Consequently, the use of the more advanced wave function-based methods is desired, but a good alternative could also be offered by the efficient double-hybrid (DH) DFT approaches, which combine KS-DFT with second-order wave function approximations.16−21

Concerning the wave function methods, the equation-of-motion coupled-cluster (EOM-CC) formalism22−26 is a popular computational tool for calculating electronic excited states of molecules. It is based on the similarity transformation of the electronic Hamiltonian, and the resulting effective operator is diagonalized to produce final state wave functions and energies. One of the most significant advantages of the EOM-CC approach is its ability to systematically include electron correlation effects in the calculations, enabling one to achieve arbitrary accuracy within the hierarchical expansion. However, as the methods become more advanced, they also become more expensive. The EOM-CC formalism can describe a qualitatively different set of final states for an n-electron reference system. For instance, ionization processes can be studied by diagonalizing the corresponding operator in a basis of determinants containing n – 1 electrons,27−31 while electron-attached states correspond to the diagonal representation in the n + 1 particle space.32,33

Another promising approach in the field is the algebraic-diagrammatic construction (ADC) formalism.34 This method is based on the diagrammatic perturbation expansion of the polarization propagator and the Møller–Plesset (MP) partitioning of the Hamiltonian. Similar to the EOM-CC approach, the ADC formalism also permits the indirect inclusion of orbital relaxation effects through couplings to higher-excited configurations. Originally, for VIP and VEA calculations, the ADC methods were elaborated based on the perturbative self-energy expansion of the Dyson equation.35 However, this led to computationally inefficient schemes as the electron attachment and detachment parts of the propagator are coupled. To address this issue, non-Dyson ADC schemes were later proposed,36,37 which allow for independent calculations of VIPs and VEAs. The effective implementation and comprehensive investigation of the ADC methods is still an active research field.38−44

Further Dyson propagator methods must also be mentioned,45 which are not strictly related to the ADC formalism. These methods are based on an approximation of the self-energy matrix, where the diagonal elements of the corresponding matrix represent a correlated, energy-dependent potential which is felt by the electrons assigned to canonical molecular orbitals (MOs). In the simplest approaches, the mixing of canonical orbitals in the Feynman–Dyson amplitudes is prevented by neglecting the non-diagonal elements of the self-energy matrix.46,47 Later, several renormalized methods with more flexible non-diagonal self-energies have also been developed.47−50 The performance of such methods has been demonstrated in excellent studies.47,51

In the previously mentioned methods, VIPs and VEAs are calculated directly in a single calculation. The so-called energy difference or Δ-approaches, however, follow a significantly different scheme, where the corresponding quantities are obtained as the difference between the total energy of the neutral and charged system computed in two separate calculations using the ground-state approximation. Depending on the applied method, several different approaches can be defined, such as the self-consistent field (ΔSCF),52−54 ΔMP,52 and ΔCC55−57 methods. The major drawback of these approaches is that the optimization of the non-Aufbau determinant can easily lead to variational collapse. Moreover, the resulting excited states are not orthogonal to the ground state, which means that the evaluation of transition matrix elements is highly problematic. In addition, higher-order Δ-approaches often require additional calculations to help the selection of the reference determinant for a desired state. In order to avoid misunderstandings, we would like to note that other ΔMP methods have also been developed.58,59 In these cases, the VIPs and VEAs are defined as the difference in the MP correlation energy between the natural and charged systems, which both are described with the orbitals and orbitals energies obtained for the n-electron system.

Concerning DH DFT, so far the most widespread option to compute VIPs and VEAs has been to employ this simple but less favorable approach. The performance of DHs for VIPs and VEAs utilizing the Δ-approach is well-documented in the literature. For the interested reader, we recommend the diverse GMTKN55 benchmark study,60 where the performance of several popular DHs is tested for well-established benchmark compilations using theoretically back-corrected experimental reference values61,62 and is also assessed against numerous pure and hybrid functionals. At the same time, we would like to note that numerous developments have taken place in the field recently. One of the most notable attempts is the orbital-optimized DH scheme using the optimized-effective-potential method,63 for which a range-separated version was also elaborated.64 In these cases, the VIPs and VEAs are obtained by calculating derivatives of the total energy by finite differences using fractional electron numbers.65−67 Another direct method has also been developed68 which is based on a more general extension of the second-order energy derivative with respect to occupation numbers,69 while the combination of the extended Koopmans’ theorem and the adiabatic connection formalism is also noteworthy.70

In this paper, a somewhat different route is followed, and the time-dependent DFT (TDDFT) formalism is extended to directly calculate VIPs and VEAs within the DH theory. We first provide a brief overview of the time-dependent approaches used, including a discussion of the genuine formalism of DH TDDFT theory and a more advanced iterative scheme. Thereafter, the corresponding working equations and efficient implementations for VIPs and VEAs are presented in detail. As we will see, the presented perturbative approach can be considered as a simplified version of the scheme introduced in ref (63). Finally, state-of-the-art and popular functionals are tested on benchmark compilations, and the performances of the methods are comprehensively assessed.

2. Theoretical Overview

2.1. Double-Hybrid Density Functional Theory for Excitations

The DH theory surpasses popular hybrid TDDFT calculations by incorporating the impact of double excitations. Similar to ground-state calculations,16 excitation energies within the genuine formalism71 are obtained in a two-step manner. First, in the most common and convenient approach, a Hermitian eigenvalue equation relying on the Tamm–Dancoff approximation (TDA)72 is solved as

2.1. 1

where ADH denotes the corresponding DH Jacobian, c is the singles excitation vector, and ωTDA is the TDA excitation energy. Using the spatial-orbital representation, the elements of the Jacobian are defined by

2.1. 2

where i, j, ... (a, b, ...) denote occupied (unoccupied) molecular orbitals, and εa and εi are the corresponding orbital energies. (ia|jb) is a two-electron repulsion integral in Mulliken’s convention, whereas (ia|fX|jb) and (ia|fC|jb) are the integrals of the exchange and correlation kernels, respectively. The above expression contains two adjustable parameters: the ratio of the Hartree–Fock (HF) and DFT contributions to the exchange energy is handled by αX, while the DFT correlation part is scaled by 1 – αC. The excitation energies obtained in this way have just hybrid quality. With the solution of eq 1 at hand, in the second step, the second-order correction is calculated perturbatively relying on the configuration interaction singles (CIS)73 with perturbative doubles [CIS(D)]74 approach. Accordingly, the improved excitation energy at the DH level is obtained as

2.1. 3

where ω(D) is the perturbative correction. The thorough theoretical background of genuine excited-state DH approaches has been presented in excellent papers,71,75−77 while the efficient calculation of the second-order terms invoking the density fitting (DF) approximation has been detailed in our previous work.78

Nowadays, one of the most prominent second-order approaches is the second-order ADC [ADC(2)] method79,80 as it offers an appropriate compromise between accuracy and computational cost.81 In practice, a nonlinear eigenvalue equation is solved iteratively as

2.1. 4

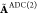where Inline graphic is the so-called effective ADC(2) Jacobian and ωADC(2) denotes the ADC(2) excitation energy. The corresponding Jacobian can be split into two parts as

2.1. 5

where ACIS is the CIS Jacobian, and all of the terms including second-order contributions are collected into matrix A[2].

Similar to CIS(D), an ADC(2)-based DH analogue can also be defined.82 In the former case, the CIS excitation energy and singles excitation vector are replaced by the quantities obtained by eq 1, and the second-order correction is scaled by an empirical factor and added to the final excitation energy. For the ADC(2)-based approach, the ADC(2) Jacobian is modified in a very similar way. That is, the CIS Jacobian in eq 5 is replaced by the DH Jacobian defined by eq 2, while the second-order terms are scaled by an empirical factor:

2.1. 6

In contrast to the genuine formalism, where the doubles correction is added a posteriori to the TDA excitation energy, these excitations are treated iteratively in this ansatz. Thus, an improvement in the calculated excitation energies is expected. Additionally, the transition properties, such as oscillator strengths, can be calculated at a higher level using the presented approach. Needless to say, the computational cost also increases since the ADC(2)-based approach is iterative.

In recent years, significant developments have been made in the DH theory. First, the spin-scaling techniques have been extended to excited-state calculations as well.76 In this case, the opposite-spin and same-spin contributions to the second-order correction are scaled separately,83−88 which enables higher flexibility of the energy functional. It is also noteworthy that the computational scaling of the spin-opposite-scaled (SOS) variant, where the same-spin contributions are completely neglected, can be reduced to N4 invoking the DF approximation for the electron-repulsion integrals and Laplace transform-based techniques,88 whereas the scaling of the original and spin-component-scaled (SCS) variants are N5, where N is a measure of the system size.

Later, to remedy the wrong long-range behavior of global exchange-correlation (XC) functionals, long-range corrected (LC) and range-separated (RS) DH functionals have been introduced.78,89 In these approaches, the Coulomb operator is split into long- and short-range components using a range-separation parameter. For the RS-DH approaches,78 both the exchange and correlation contributions are separated, while only the former one is split for LC DHs.89 These approaches can arbitrarily be combined with spin-scaling techniques,77,90 whereas their generalization to the ADC(2)-based formalism is also fairly straightforward.91

In the following sections, we discuss the extension of DH TDDFT theory to ionized and electron-attached states. Since a TDDFT calculation with a pure or hybrid functional just returns (the negative of) the corresponding orbital energies, this practically requires the generalization of the CIS(D) and ADC(2) methods to VIP and VEA calculations. We also present the working equations for an efficient, DF-based implementation. The adaptation of the approaches for spin-scaled and range-separated functionals is not discussed in detail; the derivation of the corresponding equations is straightforward based on our previous publications.78,90,91

2.2. VIP and VEA Calculations for CIS(D)

We start our proposition with the evaluation of the second-order correction for the ground state, which is required for the subsequent discussion of the excited-state corrections. Assuming a closed-shell system and spatial orbitals, the second-order MP (MP2) correlation energy is defined by

2.2. 7

where the MP2 doubles amplitudes, tijab, can be obtained by acting the Inline graphic operator on the HF reference determinant, Φ0:

2.2. 8

where Φijab is the corresponding double substitution, and the orbital energy differences Dij are constructed as εi + εj – εa – εb. Using the DF approximation, the four-center quantities can be recast as

2.2. 9

where P and Q stand for the elements of the auxiliary basis, whereas IiaP and VPQ are three- and two-center Coulomb integrals, respectively, and VPQ is a simplified notation for the corresponding element of the inverse of the two-center Coulomb integral matrix. Usually, the matrix K with elements Kia,jb = (ia|jb) is factorized as K = IV–1/2V–1/2IT = JJT. Using the latter notation, the MP2 correlation energy can be expressed in the following simple form:

2.2. 10

where the intermediate YiaQ is defined by the contraction of the three-center integrals and the antisymmetrized amplitudes.

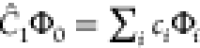For the extension of the genuine DH TDDFT approach to electron-attached/detached states, the generalization of CIS(D) to such states is required. First, we note that the CIS method73 can formally be generalized to calculate VIPs and VEAs. Concerning the former, using a generic ionization operator, Inline graphic, the ionized state can be expanded as a linear combination of singly ionized determinants: Inline graphic. Projecting onto the subspace of ionized determinants, the following eigenvalue equations are obtained:

2.2. 11

Here, the eigenvalues of this equation correspond to the negative occupied orbital energies as VIPs, while the eigenvectors are orthogonal unit vectors. The second-order (D) correction for the ionization of the k̅th orbital can be interpreted as a CIS(D)74 calculation using the corresponding ionized determinant:

2.2. 12

where the final state can be obtained as

2.2. 13

while the action of the double excitation operator on the reference yields

2.2. 14

As the disconnected terms in the second contribution to eq 12 yield the MP2 energy, the final perturbative correction to the VIP is given as

2.2. 15

where the elements of the Inline graphic-related intermediate Vija can be expressed as

2.2. 16

while the remaining 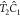Inline graphic-related contribution of eq 12 is simply calculated as

2.2. 17

We note that these equations retrieve the second-order self-energies in the diagonal and frequency-independent approximations, which correspond to the ΔMP2 method.58,59,92,93 Accordingly, a similar DH ansatz is recovered from the optimized-effective-potential method of Toulouse and co-workers63,64 if the variation of the orbitals and orbital energies in the MP2 correlation energy is neglected when taking the derivative of the total energy with respect to n.

As can be seen, in contrast to the standard excited-state CIS(D) equations, the most demanding operations are proportional to N4. Since one of the occupied indices on the right-hand side of eq 16 is restricted to the ionized orbital, the computation of Vija scales as NoccNunoccNaux, where Nocc, Nunocc, and Naux are the number of occupied, unoccupied, and auxiliary orbitals, respectively. The rate-determining step of eq 17 is the evaluation of intermediate Y, which also requires only a fourth-power scaling operation due to the restriction. This means that the cost of the perturbative second-order correction is comparable to a single iteration in a ground-state HF calculations. In addition, the unoccupied–unoccupied block of the three-center integrals is not required for the calculations, which is not true for standard CIS(D) calculations.

Similar equations are obtained for the electron-attached states. In this case, for the first-order equations, the energy of the unoccupied orbitals is retrieved as VEAs. The second-order (D) correction for the c̅th orbital is calculated as

2.2. 18

where the wave function of the n + 1-electron state is expressed as

2.2. 19

while the corresponding Inline graphic operator generates the higher-order excitations:

2.2. 20

The final (D) correction to the VEA is obtained as

2.2. 21

In this case, the intermediate Viab can be written in the

2.2. 22

form, while the intermediate X can be calculated as

2.2. 23

Again, the rate-determining steps of the above scheme, that is the calculation of Viab and 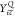Inline graphic, scale as N4.

2.3. VIP and VEA Calculations for ADC(2)

For the ADC(2) part of the DH calculation, we propose to employ the non-Dyson ADC approach of Schirmer and co-workers.36,37 The working equations for VIPs within the non-Dyson ADC schemes up to third order have been previously presented in the literature.38 However, an effective implementation relying on the DF approximation has not yet been published. Additionally, even though the derivation of the equations is fairly straightforward, the expressions for VEAs have not been presented. To remedy this, the most important expressions are collected herein.

For VIP calculations, the elements of the vector 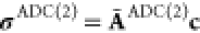Inline graphic are given as

2.3. 24

The resulting terms are very similar to those obtained for CIS(D). However, as the solutions of the corresponding eigenvalue equation are not unit vectors, the final state is properly expanded as Φn–1 = ∑iciΦi ≠ ∑iδijΦi. Accordingly, the elements of intermediate Vija can be expressed as

2.3. 25

In addition, the leading complexity of the expressions is somewhat higher compared to that obtained for CIS(D). That is, the rate-determining step of the above procedure is also the evaluation of intermediate Y, but the restriction regarding the ionized orbital cannot be applied in this case. This implies that the most expensive step is proportional to N5; however, it has to be carried out only once, regardless of the number of ionized states. The iterative procedure still scales as N4 since the intermediate in parentheses can be evaluated before it. In addition, the demanding JabQ-type integrals are not required for the calculations.

For VEAs, the elements of the Jacobi matrix transformation read explicitly as

2.3. 26

where Viab is calculated as

2.3. 27

As can be seen, similar findings can be stated regarding the scaling of the procedure as those obtained for VIPs.

The anticipated benefit of the ADC(2)-based formalism over the CIS(D)-based one is twofold. First, as the singles coefficients are relaxed during the iterative procedure, an improvement in the calculated VIPs and VEAs is expected. Second, other quantities, such as Dyson orbitals and pole strengths,94−96 can be calculated at a higher level taking into account the effect of double excitations. As the perturbative (D) correction is only an energy correction for the CIS(D)-based approaches, the aforementioned quantities have only hybrid quality. This implies that pole strengths are always equal to unity in these cases. The calculation of pole strengths for ADC(2)-based DH approaches is fairly straightforward. Similar modifications for transition density matrices have already been discussed in ref (82). That is, the first-order contributions to the spectroscopic amplitude vector are kept unchanged, while all the second-order contributions are scaled by αC. The working equations to calculate pole strengths for ADC(2) can be found in ref (38).

3. Computational Details

3.1. Calculation of the Numerical Results

In this study, the Mrcc suite of quantum chemical programs97 was used to calculate VIPs and VEAs, and TDDFT calculations were carried out using TDA. To tackle the corresponding ionized and electron-attached states, a modified Davidson algorithm using the root-following technique98 was adopted. Dunning’s correlation consistent basis sets (cc-pVXZ, where X = D and T)99,100 and their diffuse function augmented variants (aug-cc-pVXZ)101 were employed for the calculations, and the DF approximation was utilized for both the ground and attached/detached states. For this purpose, the corresponding auxiliary bases of Weigend and co-workers102−104 were employed. The frozen core approximation was employed in a similar manner to the original benchmark studies (see Sect. 3.2) in the post-KS/HF steps. The convergence threshold for the energies was set to 10–6 Eh, while the default adaptive integration grid of the Mrcc package was used for the XC contributions.105

For the calculations, the exchange and correlation functionals of Perdew, Burke, and Ernzerhof (PBE),106 Becke’s 1988 exchange functional (B88),107 the correlation functional of Lee, Yang, and Parr (LYP),108 Perdew’s 1986 correlation functional (P86),109 and Becke’s 1997 exchange and correlation functionals (B97)110 were used. The built-in functionals of the Mrcc package were employed in all cases, except for the LC hybrid and LC-DH functionals, where the locally modified version of the Libxc library111,112 was utilized. The attributes of the assessed DH functionals are collected in Table 1.

Table 1. Functionals Assessed in the Benchmark Calculationsa.

Functional Exchange Correlation Class Number of parameters References
SCS-RS-PBE-P86 PBE P86 RS DH 4 (90)
SOS-RS-PBE-P86 PBE P86 RS DH 3 (90)
SCS-ωPBEPP86 PBE P86 LC DH 7 (77)
SOS-ωPBEPP86 PBE P86 LC DH 5 (77)
DSD-PBEP86 PBE P86 global DH 4 (113)
PBE0-2 PBE PBE global DH 2 (114)
SOS-PBE0-2 PBE PBE global DH 3 (115)
PBE-QIDH PBE PBE global DH 2 (116)
B2GPPLYP B88 LYP global DH 2 (117)
ωB97X-D B97 B97 LC hybrid 18 (118)
CAM-B3LYP B88 LYP LC hybrid 3 (119)
PBE0 PBE PBE global hybrid 1 (120)
Open in a new tab
a

Both the CIS(D)- and ADC(2)-based approaches are discussed for all the DH functionals, except for SOS/SCS-ωPBEPP86. For more details regarding the ADC(2)-based formalism, see refs (82) and (91).

To gain some insight into the performance of the corresponding methods for valence excitations, we recommend comprehensive benchmark studies77,90,91,121 for the interested readers.

The errors utilized for the evaluation of the VIPs and VEAs are calculated by subtracting the reference values from the computed ones. The statistical error measures presented in the figures are the mean absolute errors (MAEs), standard deviations (SDs), and maximum absolute errors (MAXs). All the computed raw energies are available in the Supporting Information (SI). In addition, the mean errors, deviations spans, and root-mean-square errors are also included.

3.2. The Benchmark Sets

Three different benchmark sets were selected from the literature to assess the performance of the methods, and currently, these compilations are regarded as the most comprehensive ones for VIP and VEA calculations. First, we discuss the benchmark compilation of Sherrill et al.,122 which contains 24 medium-sized organic acceptor molecules. This test set incorporates the first VIPs and VEAs of the corresponding systems. References obtained at the CCSD(T)/aug-cc-pVDZ level are used in this study, invoking the frozen core approximation.

Thereafter, the test set originally compiled by Bartlett and co-workers is analyzed.123 Since this compilation was later simplified by Ortiz et al.,47 it is hereafter referred to as the BO benchmark set. The final set includes 170 valence ionized states of 33 small molecules using CCSDT/cc-pVTZ results as the reference. As can be seen, this test set contains several VIPs associated also with lower-lying valence orbitals. In contrast to the statistics presented in ref (124), all the VIPs are considered in this study. Similar to the original work,123 the core electrons were correlated during the calculations.

Finally, the performance of the functionals for biochemically relevant systems is assessed. A benchmark compilation containing nucleobases was proposed by Śmiga and co-workers.125 Recently, high-level VIPs and VEAs were computed by Tajti et al.124 using a composite reference at the complete basis set (CBS) limit. As the CBS extrapolation is not trivial for DH-TDDFT calculations, in this study, values obtained at the CCSD(T)(a)*/cc-pVDZ level are used as the references. The benchmark set incorporates six electron-attached/detached states of five different molecules.

4. Results and Discussion

In this section, the performance of the considered functionals is assessed. The results are discussed mainly from two aspects. First, the benefits of the ADC(2)-based formalism are compared with the CIS(D)-based one. Second, the effects of the DH formalism are examined in comparison with the corresponding wave function-based approaches. The importance of the spin-scaling techniques has already been emphasized by Tajti et al.124 Accordingly, we do not discuss the outcomes from this aspect, especially for the wave function-based methods.

4.1. The Acceptor Test Set

The acceptor test set of Sherrill and co-workers122 is discussed first. The error measures corresponding to the VIPs are visualized in Figure 1. Upon examining the MAEs, one can see that the highest accuracy is achieved by CCSD, with a MAE of 0.07 eV. These error measures for the SOS variant of ADC(2) and CIS(D), which are around 0.22 and 0.25 eV, respectively, are also acceptable. Among the ADC(2)-based DH methods, the best performances are attained by the spin-scaled RS-DH functionals. The MAEs for the SOS and SCS variants are 0.16 and 0.18 eV, respectively, while for SOS-PBE0-2, it is still around 0.30 eV. However, for the remaining functionals, the error exceeds 0.50 eV. It is somewhat surprising for DSD-PBEP86, which also contains spin-scaling parameters. Regarding the CIS(D)-based DH approaches, it can be concluded that the ADC(2)-based counterpart consistently outperforms the genuine variants. Nevertheless, SCS/SOS-ωPBEPP86 yields excellent results with MAEs of 0.12 and 0.15 eV. In addition, ωB97X-D is also outstanding with a MAE of 0.16 eV, while the error is significantly larger for CAM-B3LYP. A somewhat more balanced performance can be observed for the ADC(2)- and CIS(D)-based variants if the SDs and MAXs are considered. In this case, the SDs for the ADC(2)-based approaches range between 0.12 and 0.18 eV, while for the CIS(D)-based ones, they are between 0.14 and 0.22 eV. The MAXs for the most reliable DH methods are approximately 0.50 eV. These results can be achieved by ωB97X-D as well. In general, we can conclude that the error measures for the best functionals are lower in comparison with the corresponding wave function-based counterpart.

Figure 1.

Figure 1

Open in a new tab

Error measures for the VIPs of the acceptor test set122 using the aug-cc-pVDZ basis set with the corresponding auxiliary bases. The MAEs (SDs) are visualized by colored (black) bars, while MAXs are presented by dots. For the sake of clarity, some outliers are omitted. The wave function (first group), ADC(2)-based DH (second group), CIS(D)-based DH (third group), and hybrid methods (fourth group) are presented in gray, blue, red, and orange, respectively. The CCSD values were taken from ref (124).

Continuing the previous study, the error measures regarding the VEAs are presented in Figure 2. As can be seen, it is difficult to compete with the CCSD, SOS-CIS(D), and SOS-ADC(2) approaches. The lowest MAE, precisely 0.05 eV, is attained by CCSD, while the errors are still around 0.10 eV for SOS-CIS(D) and SOS-ADC(2). Among the ADC(2)- and CIS(D)-based DH functionals, the best performances are provided by the SOS-RS-PBE-P86 functionals. Unfortunately, in these cases, the MAEs are 0.40 and 0.46 eV, respectively. Nevertheless, these values are somewhat lower than those obtained for the standard ADC(2) and CIS(D) methods. This is also true for SOS-PBE0-2, while the remaining DH functionals have significantly higher MAEs. Acceptable performance is achieved by ωB97X-D, with a MAE of 0.44 eV. Inspecting the SDs, a somewhat more balanced picture can be obtained. The precision of CCSD is still outstanding with an SD of 0.06 eV; however, the other methods are very close to each other. That is, the SDs are 0.14 and 0.17 eV for ADC(2) and CIS(D), respectively, while they are around 0.13 eV for the SOS variants. The deviations do not exceed 0.15 eV for most of the DH functionals, while some of the best performers, such as the SOS-PBE0-2 functionals, have even lower SDs compared to the SOS-ADC(2) approach. A bit larger deviation, precisely 0.19 eV, is yielded by ωB97X-D. If the MAXs are considered, the performances are very similar to those obtained for the MAEs. Accordingly, the lowest MAXs, being 0.15, 0.24, and 0.27 eV, are achieved by CCSD, SOS-CIS(D), and SOS-ADC(2), respectively. These excellent results cannot be approached by any other methods. That is, the same measures are 0.85 and 0.97 eV for the standard ADC(2) and CIS(D) approaches, respectively. Among the DH functionals, the best results are provided by the ADC(2)- and CIS(D)-based SOS-RS-PBE-P86, with MAXs of 0.69 and 0.77 eV, respectively, while it is 0.76 eV for ωB97X-D.

Figure 2.

Figure 2

Open in a new tab

Error measures for the VEAs of the acceptor test set122 using the aug-cc-pVDZ basis set with the corresponding auxiliary bases. See the caption of Figure 1 for further details.

4.2. The Bartlett/Ortiz Test Set

Thereafter, the comprehensive BO benchmark set47,123 is assessed. The main error measures are collected in Figure 3. Upon inspection of the error bars, we can conclude that the best results are achieved by the CCSD and ADC(2)-based SOS-RS-PBE-P86 approaches, with MAEs of 0.24 eV. The performance of the SOS-ADC(2) and the SCS variant of the former functional is also outstanding, with error measures that do not exceed 0.30 eV. In addition, the CIS(D)-based variants of the SOS/SCS-RS-PBE-P86, SOS-PBE0-2, and SCS/SOS-ωPBEPP86 functionals can also be deemed reliable. Overall, the CIS(D)-based approaches are slightly outperformed by the ADC(2)-based ones. For this benchmark set, the ωB97X-D functional is not outstanding at all. The MAE is 1.10 eV, which is significantly higher in comparison with the best DH approaches. Similar rankings can be determined when considering SDs. Among the wave function-based methods, the most precise results are provided by CCSD, with an SD of 0.23 eV, while an SD of 0.34 eV is obtained for the SOS-ADC(2) approach. In this regard, the performance is more balanced for the DH functionals. The lowest SD, which is 0.29 eV, is attained by the ADC(2)-based SOS-RS-PBE-P86 method, while an SD of around 0.35 eV is achieved by the remaining best performers. Again, this error measure is noticeably higher for ωB97X-D, with an SD of 0.51 eV. Upon examination of the MAXs, the lowest value of 1.32 eV is obtained for the ADC(2)-based SOS-PBE0-2 approach, while a MAX of 1.33 eV is attained by SOS-ADC(2). The ADC(2)-based SOS-RS-PBE-P86 is also outstanding, with an error of 1.53 eV, but most of the DH functionals are reliable, as the MAXs do not exceed 2.00 eV, whereas it is 1.81 for CCSD. A somewhat higher value, precisely 2.64 eV, is obtained for ωB97X-D.

Figure 3.

Figure 3

Open in a new tab

Error measures for the VIPs of the BO test set47,123 using the cc-pVTZ basis set with the corresponding auxiliary bases. See the caption of Figure 1 for further details.

4.3. Nucleobases

Finally, the performances for the nucleobases124,125 are discussed. The error measures corresponding to the VIPs are presented in Figure 4. On the basis of the numerical results, surprisingly, the ADC(2)-based SOS-PBE0-2 and ωB97X-D are the best performers, with MAEs of 0.11 eV. Similarly, outstanding accuracy is achieved by the SOS-ADC(2) and ADC(2)-based SOS-RS-PBE-P86 methods, while the CCSD and SOS-ωPBEPP86 approaches also seem to be reliable. In these cases, the MAEs are below 0.15 eV. Comparing the ADC(2)- and CIS(D)-based functionals, again, the former ones outperform the latter ones. When examining the SDs, similar conclusions can be drawn. That is, excellent precision is observed for the SOS-PBE0-2 functionals, with deviations of around 0.06 eV, and CCSD also achieves a similar result. In this regard, the ADC(2)-based methods provide more balanced values. The SD is approximately 0.15 eV for the remaining DH functionals, which is highly acceptable, while a bit larger values are obtained for the ωB97X-D and the CIS(D)-based approaches, except for SOS-ωPBEPP86. The MAXs are also well-balanced for the best DHs, ranging between 0.24 and 0.36 eV, while it is 0.64 eV for ωB97X-D.

Figure 4.

Figure 4

Open in a new tab

Error measures for the VIPs of the nucleobases124,125 using the cc-pVDZ basis set with the corresponding auxiliary bases. See the caption of Figure 1 for further details.

The results for the electron-attached states of the nucleobases are collected in Figure 5. As can be seen, again, CCSD and the SOS variants of the wave function-based methods outperform the DH functionals. However, the differences are somewhat less pronounced than those obtained for the acceptor test set. That is, the lowest MAE, 0.06 eV, is attained by CCSD, while the SOS-ADC(2) and SOS-CIS(D) approaches achieve MAEs of 0.16 and 0.19 eV, respectively. Among the DH methods, the most accurate approach is the ADC(2)-based SOS-RS-PBE-P86, with a MAE of 0.30 eV. In addition, the CIS(D)-based counterpart is also superior in its class. The SCS variant of the former functionals, as well as the SOS-PBE0-2 and SCS/SOS-ωPBEPP86 methods provide acceptable performance. In these cases, the MAEs do not exceed 0.50 eV. For the remaining DH functionals, significantly higher errors are obtained, while the MAE is 0.37 eV for the ωB97X-D method. Upon examining the SDs, an interesting behavior can be observed. Regarding the DH approaches, the lowest deviations are yielded by the methods that are the most inaccurate. For instance, B2GPPLYP has an SD of 0.13 eV, while this value is larger even for SOS-ADC(2). The deviations are around 0.26 eV for the most accurate ADC(2)-based approaches, while they are approximately 0.30 eV for the CIS(D)-based counterparts. A similar precision is achieved by ωB97X-D, with an SD of 0.35 eV. The lowest MAX, being 0.22 eV, is reached by CCSD, while SOS-ADC(2) and SOS-CIS(D) are also outstanding in this regard. The maximum errors are 0.40 eV for the SOS second-order wave function methods. The performance of the best DH functionals is well-balanced within each class. The MAXs are around 0.70 eV for the ADC(2)-based approaches, while they are roughly 0.85 eV for the CIS(D)-based ones. For the hybrid functionals, the lowest MAX, precisely 0.93 eV, is attained by ωB97X-D.

Figure 5.

Figure 5

Open in a new tab

Error measures for the VEAs of the nucleobases124,125 using the cc-pVDZ basis set with the corresponding auxiliary bases. See the caption of Figure 1 for further details.

For this benchmark set, the effect of the second-order correction is also assessed. This study is also intriguing due to the fact that orbital energies can be interpreted as VIPs and VEAs within Koopmans’ theorem. However, it is important to keep in mind that these values only offer a simplified approximation of the corresponding quantities as the relaxation effects are neglected. For the VIPs, the mean errors are collected in Figure 6, while the corresponding chart for the VEAs can be found in the SI. Considering the negative values of occupied orbital energies, it can generally be concluded that VIPs are consistently overestimated. This is also true for the wave function-based methods. The second-order correction, to some extent, systematically reduces the VIP values. As can be seen, the methods that are least accurate inspecting the orbital energies, such as SOS-ADC(2), ADC(2)-based SOS-RS-PBE-P86, and SCS-ωPBEPP86, actually provide the most accurate VIPs in terms of the final result. In contrast, for methods where VIPs can be precisely described by the negative of orbital energies, such as DSD-PBEP86 and B2GPPLYP, the second-order correction significantly reduces the corresponding values, leading to inaccurate results for the DH calculations. Similar findings can be reported if VEAs are inspected; however, the effects are opposite to what was observed for VIPs. For the most precise methods, virtual orbital energies significantly underestimate VEAs, and the second-order correction systematically increases their values. For the (SOS-)PBE0-2 and DSD-PBEP86 methods, VEAs can be precisely described by the virtual orbital energies, while for the least accurate methods, such as B2GPPLYP, the orbital energies are already overestimated.

Figure 6.

Figure 6

Open in a new tab

Mean errors for the VIPs of the nucleobases using the aug-cc-pVDZ basis sets with the corresponding auxiliary bases. Errors calculated from the orbital energies (final DH results) are visualized by the darker (lighter) bars. The wave function (first group), ADC(2)-based DH (second group), and CIS(D)-based DH (third group) methods are presented in gray, blue, and red, respectively.

4.4. Overall Performance

It is hard to characterize the performance of the methods with a single measure. Recently, a very simple procedure was suggested by Casanova-Páez and Goerigk.77 In their original paper, the MAEs obtained for the benchmark sets were simply averaged. In this study, we use the same measure separately for VIPs and VEAs. From a practical point of view, the computational cost of the approaches is also important. In order to help with the selection of methods worth applying, the overall performance of the best approaches and the rate-determining steps of the calculations are collected in Table 2. Inspecting the results, we can conclude that the most reliable method is the most expensive CCSD, while the SOS-ADC(2) approach is also outstanding. Among the functionals, the most robust performance is attained by the ADC(2)-based SOS-RS-PBE-P86 method. For ionization potentials, it outperforms SOS-ADC(2), and almost CCSD quality can be achieved. This method also provides the lowest overall MAE for VEAs; however, the accuracy is far below that obtained for CCSD or SOS-ADC(2). As a cost-effective alternative, SOS-ωPBEPP86 is also recommended for VIPs, but its performance is even less reliable for electron-attached states.

Table 2. Averaged MAEs for VIPs and VEAs, as Well as the Number of Independent Parameters and the Scaling of the Rate-Determining Steps on Top of the KS/HF Solution for the Best Performers.

    MAE
   Scaling
Class Method VIP VEA Number of parameters Ground state VIP/VEA
wave function-based CCSD 0.153 0.051 – iterative N6 iterative N5
  SOS-ADC(2) 0.211 0.135 1 perturbative N4 iterative N4
  SOS-CIS(D) 0.325 0.146 1 perturbative N4 perturbative N4
  ADC(2) 0.585 0.431 – perturbative N5 iterative N4
  CIS(D) 0.834 0.492 – perturbative N4 perturbative N4
ADC(2)-based DH SCS-RS-PBE-P86 0.212 0.458 4 perturbative N5 iterative N4
  SOS-RS-PBE-P86 0.182 0.354 3 perturbative N4 iterative N4
  SOS-PBE0-2 0.300 0.506 3 perturbative N4 iterative N4
CIS(D)-based DH SCS-RS-PBE-P86 0.328 0.511 4 perturbative N4 perturbative N4
  SOS-RS-PBE-P86 0.306 0.396 3 perturbative N4 perturbative N4
  SCS-ωPBEPP86 0.256 0.683 7 perturbative N4 perturbative N4
  SOS-ωPBEPP86 0.226 0.552 5 perturbative N4 perturbative N4
  SOS-PBE0-2 0.352 0.518 3 perturbative N4 perturbative N4
LC hybrid ωB97X-D 0.457 0.406 18 – –
  CAM-B3LYP 0.924 1.121 3 – –
Open in a new tab

5. Conclusions

In this study, double-hybrid time-dependent density functional theory has been extended to directly calculate vertical ionization potentials and electron affinities. The approach has been presented for the genuine variant of the DH TDDFT theory,71 where the second-order correction is calculated perturbatively relying on the CIS(D) method. In addition, our ADC(2)-based DH variant82 has also been considered, where the double excitations are treated iteratively. It has been demonstrated that the costs of the VIP and VEA calculations with the CIS(D)-based DHs are just comparable to one KS iteration step per state, while for the ADC(2)-based ones, the most demanding step is proportional to N5. However, it has to be carried out only once, regardless of the number of tackled states, and the iterative procedure still scales as N4. For a detailed comparison, state-of-the-art RS-DH and LC-DH methods, including spin-scaling techniques, were selected, as well as robust and popular hybrid and global DH approaches were also included. To assess the performance of the functionals, comprehensive benchmark calculations were carried out on the best available test sets. A total of 224 electron-detached and 54 electron-attached states were examined, with references provided by higher-order coupled-cluster calculations that include triple excitations.

The findings were analyzed from two main perspectives. First, the robustness of the ADC(2)-based ansatz was inspected in contrast to the CIS(D)-based approach. In this regard, the advantages of the more advanced formalism are clearly demonstrated. Second, the impact of the DH approach was assessed in comparison with the corresponding wave function-based methods. The excellent performance of SOS-ADC(2) had already been revealed by Tajti and co-workers.124 Accordingly, the efficiency of the approaches is compared to this starting point. Our numerical results show that, among the functionals, the most robust performance is attained by the ADC(2)-based SOS-RS-PBE-P86 approach. This method consistently outperforms SOS-ADC(2) for ionization potentials; furthermore, CCSD quality can also be reached. Unfortunately, the results are not so encouraging for electron affinities. Even though the best performance is achieved by the above functional, the accuracy is far below that obtained for SOS-ADC(2). For ionization potentials, the CIS(D)-based SOS-ωPBEPP86 is also recommended, while SOS-PBE0-2 is identified as the most reliable global DH functional. The importance of spin-scaling techniques was confirmed by this study as well, though the performance of DSD-PBEP86 is found to be somewhat disappointing. In addition, surprisingly good results were revealed for ωB97X-D, where the VIPs/VEAs are associated with the corresponding Kohn–Sham orbital energies within the present formalism. Nevertheless, ωB97X-D does not outperform the DHs concerning robustness.

Acknowledgments

The work of D.M. is supported by the NKFIH PD142372 grant and the ÚNKP-22-4-II-BME-157 New National Excellence Program of the Ministry for Culture and Innovation from the source of the National Research, Development, and Innovation Fund. M.K. is grateful for the financial support from the National Research, Development, and Innovation Office (NKFIH, Grant No. KKP126451). The research reported in this paper is part of project BME-EGA-02, implemented with the support provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021 funding scheme. The computing time granted on the Hungarian HPC Infrastructure at NIIF Institute, Hungary is gratefully acknowledged.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00363.

  • Computed vertical ionization potentials and electron affinities (XLSX)

The authors declare no competing financial interest.

Supplementary Material

ct3c00363_si_001.xlsx (238KB, xlsx)

References

  1. Yeh N.; Yeh P. Organic solar cells: Their developments and potentials. Renew. Sust. Energy Rev. 2013, 21, 421. 10.1016/j.rser.2012.12.046. [DOI] [Google Scholar]
  2. Poelking C.; Benduhn J.; Spoltore D.; Schwarze M.; Roland S.; Piersimoni F.; Neher D.; Leo K.; Vandewal K.; Andrienko D. Open-circuit voltage of organic solar cells: interfacial roughness makes the difference. Commun. Phys. 2022, 5, 307. 10.1038/s42005-022-01084-x. [DOI] [Google Scholar]
  3. Delgado J. L.; Bouit P.-A.; Filippone S.; Herranz M. A. Á.; Martín N. Organic photovoltaics: a chemical approach. Chem. Commun. 2010, 46, 4853. 10.1039/c003088k. [DOI] [PubMed] [Google Scholar]
  4. Alizadeh E.; Sanche L. Precursors of Solvated Electrons in Radiobiological Physics and Chemistry. Chem. Rev. 2012, 112, 5578. 10.1021/cr300063r. [DOI] [PubMed] [Google Scholar]
  5. Alizadeh E.; Orlando T. M.; Sanche L. Biomolecular Damage Induced by Ionizing Radiation: The Direct and Indirect Effects of Low-Energy Electrons on DNA. Annu. Rev. Phys. Chem. 2015, 66, 379. 10.1146/annurev-physchem-040513-103605. [DOI] [PubMed] [Google Scholar]
  6. Kumar A.; Becker D.; Adhikary A.; Sevilla M. D. Reaction of Electrons with DNA: Radiation Damage to Radiosensitization. Int. J. Mol. Sci. 2019, 20, 3998. 10.3390/ijms20163998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Zheng Y.; Cloutier P.; Hunting D. J.; Sanche L.; Wagner J. R. Chemical Basis of DNA Sugar–Phosphate Cleavage by Low-Energy Electrons. J. Am. Chem. Soc. 2005, 127, 16592. 10.1021/ja054129q. [DOI] [PubMed] [Google Scholar]
  8. Dong Y.; Gao Y.; Liu W.; Gao T.; Zheng Y.; Sanche L. Clustered DNA Damage Induced by 2–20 eV Electrons and Transient Anions: General Mechanism and Correlation to Cell Death. J. Phys. Chem. Lett. 2019, 10, 2985. 10.1021/acs.jpclett.9b01063. [DOI] [PubMed] [Google Scholar]
  9. Mukherjee M.; Tripathi D.; Brehm M.; Riplinger C.; Dutta A. K. Efficient EOM-CC-based Protocol for the Calculation of Electron Affinity of Solvated Nucleobases: Uracil as a Case Study. J. Chem. Theory Comput. 2021, 17, 105. 10.1021/acs.jctc.0c00655. [DOI] [PubMed] [Google Scholar]
  10. Verma P.; Ghosh D.; Dutta A. K. Electron Attachment to Cytosine: The Role of Water. J. Phys. Chem. A 2021, 125, 4683. 10.1021/acs.jpca.0c10199. [DOI] [PubMed] [Google Scholar]
  11. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  12. Zhan C.-G.; Nichols J. A.; Dixon D. A. Ionization Potential, Electron Affinity, Electronegativity, Hardness, and Electron Excitation Energy: Molecular Properties from Density Functional Theory Orbital Energies. J. Phys. Chem. A 2003, 107, 4184. 10.1021/jp0225774. [DOI] [Google Scholar]
  13. Perdew J. P.; Levy M. Comment on “Significance of the highest occupied Kohn–Sham eigenvalue. Phys. Rev. B 1997, 56, 16021. 10.1103/PhysRevB.56.16021. [DOI] [Google Scholar]
  14. Levy M.; Perdew J. P.; Sahni V. Exact differential equation for the density and ionization energy of a many-particle system. Phys. Rev. A 1984, 30, 2745. 10.1103/PhysRevA.30.2745. [DOI] [Google Scholar]
  15. Zhang G.; Musgrave C. B. Comparison of DFT Methods for Molecular Orbital Eigenvalue Calculations. J. Phys. Chem. A 2007, 111, 1554. 10.1021/jp061633o. [DOI] [PubMed] [Google Scholar]
  16. Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
  17. Goerigk L.; Grimme S. Double-hybrid density functionals. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2014, 4, 576. 10.1002/wcms.1193. [DOI] [Google Scholar]
  18. Brémond É.; Ciofini I.; Sancho-García J. C.; Adamo C. Nonempirical Double-Hybrid Functionals: An Effective Tool for Chemists. Acc. Chem. Res. 2016, 49, 1503. 10.1021/acs.accounts.6b00232. [DOI] [PubMed] [Google Scholar]
  19. Martin J. M. L.; Santra G. Empirical Double-Hybrid Density Functional Theory: A ‘Third Way’ in Between WFT and DFT. Isr. J. Chem. 2020, 60, 787. 10.1002/ijch.201900114. [DOI] [Google Scholar]
  20. Su N. Q.; Xu X. The XYG3 Type of Doubly Hybrid Density Functionals. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2016, 6, 721. 10.1002/wcms.1274. [DOI] [Google Scholar]
  21. Sancho-García J. C.; Adamo C. Double-hybrid density functionals: Merging wavefunction and density approaches to get the best of both worlds. Phys. Chem. Chem. Phys. 2013, 15, 14581. 10.1039/c3cp50907a. [DOI] [PubMed] [Google Scholar]
  22. Geertsen J.; Rittby M.; Bartlett R. J. The equation-of-motion coupled-cluster method: Excitation energies of Be and CO. Chem. Phys. Lett. 1989, 164, 57. 10.1016/0009-2614(89)85202-9. [DOI] [Google Scholar]
  23. Stanton J. F.; Bartlett R. J. The equation of motion coupled-cluster method. A systematic biorthogonal approach to molecular excitation energies, transition probabilities, and excited state properties. J. Chem. Phys. 1993, 98, 7029. 10.1063/1.464746. [DOI] [Google Scholar]
  24. Watts J. D.; Bartlett R. J. The inclusion of connected triple excitations in the equation-of-motion coupled-cluster method. J. Chem. Phys. 1994, 101, 3073. 10.1063/1.467620. [DOI] [Google Scholar]
  25. Bartlett R. J. Coupled-cluster theory and its equation-of-motion extensions. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 126. 10.1002/wcms.76. [DOI] [Google Scholar]
  26. Sneskov K.; Christiansen O. Excited state coupled cluster methods. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 566. 10.1002/wcms.99. [DOI] [Google Scholar]
  27. Nooijen M.; Bartlett R. J. Similarity transformed equation-of-motion coupled-cluster theory: Details, examples, and comparisons. J. Chem. Phys. 1997, 107, 6812. 10.1063/1.474922. [DOI] [Google Scholar]
  28. Stanton J. F.; Gauss J. Perturbative treatment of the similarity transformed Hamiltonian in equation-of-motion coupled-cluster approximations. J. Chem. Phys. 1995, 103, 1064. 10.1063/1.469817. [DOI] [Google Scholar]
  29. Stanton J. F.; Gauss J. Analytic energy derivatives for ionized states described by the equation-of-motion coupled cluster method. J. Chem. Phys. 1994, 101, 8938. 10.1063/1.468022. [DOI] [Google Scholar]
  30. Pieniazek P. A.; Bradforth S. E.; Krylov A. I. Charge localization and Jahn–Teller distortions in the benzene dimer cation. J. Chem. Phys. 2008, 129, 074104. 10.1063/1.2969107. [DOI] [PubMed] [Google Scholar]
  31. Musiał M.; Kucharski S. A.; Bartlett R. J. Equation-of-motion coupled cluster method with full inclusion of the connected triple excitations for ionized states: IP-EOM-CCSDT. J. Chem. Phys. 2003, 118, 1128. 10.1063/1.1527013. [DOI] [Google Scholar]
  32. Nooijen M.; Bartlett R. J. Equation of motion coupled cluster method for electron attachment. J. Chem. Phys. 1995, 102, 3629. 10.1063/1.468592. [DOI] [Google Scholar]
  33. Musiał M.; Bartlett R. J. Equation-of-motion coupled cluster method with full inclusion of connected triple excitations for electron-attached states: EA-EOM-CCSDT. J. Chem. Phys. 2003, 119, 1901. 10.1063/1.1584657. [DOI] [Google Scholar]
  34. Schirmer J. Beyond the random-phase approximation: A new approximation scheme for the polarization propagator. Phys. Rev. A 1982, 26, 2395. 10.1103/PhysRevA.26.2395. [DOI] [Google Scholar]
  35. Schirmer J.; Cederbaum L. S.; Walter O. New approach to the one-particle Green’s function for finite Fermi systems. Phys. Rev. A 1983, 28, 1237. 10.1103/PhysRevA.28.1237. [DOI] [Google Scholar]
  36. Schirmer J.; Trofimov A. B.; Stelter G. A non-Dyson third-order approximation scheme for the electron propagator. J. Chem. Phys. 1998, 109, 4734. 10.1063/1.477085. [DOI] [Google Scholar]
  37. Trofimov A. B.; Schirmer J. Molecular ionization energies and ground- and ionic-state properties using a non-Dyson electron propagator approach. J. Chem. Phys. 2005, 123, 144115. 10.1063/1.2047550. [DOI] [PubMed] [Google Scholar]
  38. Dempwolff A. L.; Schneider M.; Hodecker M.; Dreuw A. Efficient implementation of the non-Dyson third-order algebraic diagrammatic construction approximation for the electron propagator for closed- and open-shell molecules. J. Chem. Phys. 2019, 150, 064108. 10.1063/1.5081674. [DOI] [PubMed] [Google Scholar]
  39. Banerjee S.; Sokolov A. Y. Third-order algebraic diagrammatic construction theory for electron attachment and ionization energies: Conventional and Green’s function implementation. J. Chem. Phys. 2019, 151, 224112. 10.1063/1.5131771. [DOI] [PubMed] [Google Scholar]
  40. Hodecker M.; Dempwolff A. L.; Schirmer J.; Dreuw A. Theoretical analysis and comparison of unitary coupled-cluster and algebraic-diagrammatic construction methods for ionization. J. Chem. Phys. 2022, 156, 074104. 10.1063/5.0070967. [DOI] [PubMed] [Google Scholar]
  41. Dempwolff A. L.; Hodecker M.; Dreuw A. Vertical ionization potential benchmark for unitary coupled-cluster and algebraic-diagrammatic construction methods. J. Chem. Phys. 2022, 156, 054114. 10.1063/5.0079047. [DOI] [PubMed] [Google Scholar]
  42. Dempwolff A. L.; Paul A. C.; Belogolova A. M.; Trofimov A. B.; Dreuw A. Intermediate state representation approach to physical properties of molecular electron-detached states. I. Theory and implementation. J. Chem. Phys. 2020, 152, 024113. 10.1063/1.5137792. [DOI] [PubMed] [Google Scholar]
  43. Dempwolff A. L.; Paul A. C.; Belogolova A. M.; Trofimov A. B.; Dreuw A. Intermediate state representation approach to physical properties of molecular electron-detached states. II. Benchmarking. J. Chem. Phys. 2020, 152, 024125. 10.1063/1.5137794. [DOI] [PubMed] [Google Scholar]
  44. Dempwolff A. L.; Belogolova A. M.; Trofimov A. B.; Dreuw A. Intermediate state representation approach to physical properties of molecular electron-attached states: Theory, implementation, and benchmarking. J. Chem. Phys. 2021, 154, 104117. 10.1063/5.0043337. [DOI] [PubMed] [Google Scholar]
  45. Ortiz J. V. Electron propagator theory: an approach to prediction and interpretation in quantum chemistry. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2013, 3, 123. 10.1002/wcms.1116. [DOI] [Google Scholar]
  46. Ortiz J. V. Partial third-order quasiparticle theory: Comparisons for closed-shell ionization energies and an application to the borazine photoelectron spectrum. J. Chem. Phys. 1996, 104, 7599. 10.1063/1.471468. [DOI] [Google Scholar]
  47. Corzo H. H.; Galano A.; Dolgounitcheva O.; Zakrzewski V. G.; Ortiz J. V. NR2 and P3+: Accurate, Efficient Electron-Propagator Methods for Calculating Valence, Vertical Ionization Energies of Closed-Shell Molecules. J. Phys. Chem. A 2015, 119, 8813. 10.1021/acs.jpca.5b00942. [DOI] [PubMed] [Google Scholar]
  48. Ortiz J. V. An efficient, renormalized self-energy for calculating the electron binding energies of closed-shell molecules and anions. Int. J. Quantum Chem. 2005, 105, 803. 10.1002/qua.20664. [DOI] [Google Scholar]
  49. Ortiz J. V. A nondiagonal, renormalized extension of partial third-order quasiparticle theory: Comparisons for closed-shell ionization energies. J. Chem. Phys. 1998, 108, 1008. 10.1063/1.475463. [DOI] [Google Scholar]
  50. Opoku E.; Pawłowski F.; Ortiz J. V. A new generation of diagonal self-energies for the calculation of electron removal energies. J. Chem. Phys. 2021, 155, 204107. 10.1063/5.0070849. [DOI] [PubMed] [Google Scholar]
  51. Opoku E.; Pawłowski F.; Ortiz J. V. Electron Propagator Theory of Vertical Electron Detachment Energies of Anions: Benchmarks and Applications to Nucleotides. J. Phys. Chem. A 2023, 127, 1085. 10.1021/acs.jpca.2c08372. [DOI] [PubMed] [Google Scholar]
  52. Gilbert A. T. B.; Besley N. A.; Gill P. M. W. Self-Consistent Field Calculations of Excited States Using the Maximum Overlap Method (MOM). J. Phys. Chem. A 2008, 112, 13164. 10.1021/jp801738f. [DOI] [PubMed] [Google Scholar]
  53. Bagus P. S. Self-Consistent-Field Wave Functions for Hole States of Some Ne-Like and Ar-Like Ions. Phys. Rev. 1965, 139, A619. 10.1103/PhysRev.139.A619. [DOI] [Google Scholar]
  54. Triguero L.; Pettersson L. G. M.; Ågren H. Calculations of near-edge x-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory. Phys. Rev. B 1998, 58, 8097. 10.1103/PhysRevB.58.8097. [DOI] [Google Scholar]
  55. Lee J.; Small D. W.; Head-Gordon M. Excited states via coupled cluster theory without equation-of-motion methods: Seeking higher roots with application to doubly excited states and double core hole states. J. Chem. Phys. 2019, 151, 214103. 10.1063/1.5128795. [DOI] [PubMed] [Google Scholar]
  56. Meissner L.; Balková A.; Bartlett R. J. Multiple solutions of the single-reference coupled-cluster method. Chem. Phys. Lett. 1993, 212, 177. 10.1016/0009-2614(93)87127-O. [DOI] [Google Scholar]
  57. Zheng X.; Cheng L. Performance of Delta-Coupled-Cluster Methods for Calculations of Core-Ionization Energies of First-Row Elements. J. Chem. Theory Comput. 2019, 15, 4945. 10.1021/acs.jctc.9b00568. [DOI] [PubMed] [Google Scholar]
  58. Hirata S.; Hermes M. R.; Simons J.; Ortiz J. V. General-Order Many-Body Green’s Function Method. J. Chem. Theory Comput. 2015, 11, 1595. 10.1021/acs.jctc.5b00005. [DOI] [PubMed] [Google Scholar]
  59. Hirata S.; Doran A. E.; Knowles P. J.; Ortiz J. V. One-particle many-body Green’s function theory: Algebraic recursive definitions, linked-diagram theorem, irreducible-diagram theorem, and general-order algorithms. J. Chem. Phys. 2017, 147, 044108. 10.1063/1.4994837. [DOI] [PubMed] [Google Scholar]
  60. Goerigk L.; Hansen A.; Bauer C.; Ehrlich S.; Najibi A.; Grimme S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184. 10.1039/C7CP04913G. [DOI] [PubMed] [Google Scholar]
  61. Goerigk L.; Grimme S. A general database for main group thermochemistry, kinetics, and noncovalent interactions – Assessment of common and reparameterized (meta-)GGA density functionals. J. Chem. Theory Comput. 2010, 6, 107. 10.1021/ct900489g. [DOI] [PubMed] [Google Scholar]
  62. Curtiss L. A.; Raghavachari K.; Trucks G. W.; Pople J. A. Gaussian-2 theory for molecular energies of first-and second-row compounds. J. Chem. Phys. 1991, 94, 7221. 10.1063/1.460205. [DOI] [Google Scholar]
  63. Śmiga S.; Franck O.; Mussard B.; Buksztel A.; Grabowski I.; Luppi E.; Toulouse J. Self-consistent double-hybrid density-functional theory using the optimized-effective-potential method. J. Chem. Phys. 2016, 145, 144102. 10.1063/1.4964319. [DOI] [PubMed] [Google Scholar]
  64. Śmiga S.; Grabowski I.; Witkowski M.; Mussard B.; Toulouse J. Self-Consistent Range-Separated Density-Functional Theory with Second-Order Perturbative Correction via the Optimized-Effective-Potential Method. J. Chem. Theory Comput. 2020, 16, 211. 10.1021/acs.jctc.9b00807. [DOI] [PubMed] [Google Scholar]
  65. Cohen A. J.; Mori-Sánchez P.; Yang W. Second-Order Perturbation Theory with Fractional Charges and Fractional Spins. J. Chem. Theory Comput. 2009, 5, 786. 10.1021/ct8005419. [DOI] [PubMed] [Google Scholar]
  66. Su N. Q.; Yang W.; Mori-Sánchez P.; Xu X. Fractional Charge Behavior and Band Gap Predictions with the XYG3 Type of Doubly Hybrid Density Functionals. J. Phys. Chem. A 2014, 118, 9201. 10.1021/jp5029992. [DOI] [PubMed] [Google Scholar]
  67. Mussard B.; Toulouse J. Fractional-charge and fractional-spin errors in range-separated density-functional theory. Mol. Phys. 2017, 115, 161. 10.1080/00268976.2016.1213910. [DOI] [Google Scholar]
  68. Su N. Q.; Xu X. Insights into Direct Methods for Predictions of Ionization Potential and Electron Affinity in Density Functional Theory. J. Phys. Chem. Lett. 2019, 10, 2692. 10.1021/acs.jpclett.9b01052. [DOI] [PubMed] [Google Scholar]
  69. Beste A.; Vázquez-Mayagoitia Á.; Ortiz J. V. Direct ΔMBPT(2) method for ionization potentials, electron affinities, and excitation energies using fractional occupation numbers. J. Chem. Phys. 2013, 138, 074101. 10.1063/1.4790626. [DOI] [PubMed] [Google Scholar]
  70. Gu Y.; Xu X. Extended Koopmans’ theorem in the adiabatic connection formalism: Applied to doubly hybrid density functionals. J. Chem. Phys. 2020, 153, 044109. 10.1063/5.0010743. [DOI] [PubMed] [Google Scholar]
  71. Grimme S.; Neese F. Double-hybrid density functional theory for excited electronic states of molecules. J. Chem. Phys. 2007, 127, 154116. 10.1063/1.2772854. [DOI] [PubMed] [Google Scholar]
  72. Hirata S.; Head-Gordon M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291. 10.1016/S0009-2614(99)01149-5. [DOI] [Google Scholar]
  73. Foresman J. B.; Head-Gordon M.; Pople J. A.; Frisch M. J. Toward a systematic molecular orbital theory for excited states. J. Phys. Chem. 1992, 96, 135. 10.1021/j100180a030. [DOI] [Google Scholar]
  74. Head-Gordon M.; Rico R. J.; Oumi M.; Lee T. J. A doubles correction to electronic excited states from configuration interaction in the space of single substitutions. Chem. Phys. Lett. 1994, 219, 21. 10.1016/0009-2614(94)00070-0. [DOI] [Google Scholar]
  75. Ottochian A.; Morgillo C.; Ciofini I.; Frisch M. J.; Scalmani G.; Adamo C. Double hybrids and time-dependent density functional theory: An implementation and benchmark on charge transfer excited states. J. Comput. Chem. 2020, 41, 1242. 10.1002/jcc.26170. [DOI] [PubMed] [Google Scholar]
  76. Schwabe T.; Goerigk L. Time-Dependent Double-Hybrid Density Functionals with Spin-Component and Spin-Opposite Scaling. J. Chem. Theory Comput. 2017, 13, 4307. 10.1021/acs.jctc.7b00386. [DOI] [PubMed] [Google Scholar]
  77. Casanova-Páez M.; Goerigk L. Time-Dependent Long-Range-Corrected Double-Hybrid Density Functionals with Spin-Component and Spin-Opposite Scaling: A Comprehensive Analysis of Singlet–Singlet and Singlet–Triplet Excitation Energies. J. Chem. Theory Comput. 2021, 17, 5165. 10.1021/acs.jctc.1c00535. [DOI] [PubMed] [Google Scholar]
  78. Mester D.; Kállay M. A simple range-separated double-hybrid density functional theory for excited states. J. Chem. Theory Comput. 2021, 17, 927. 10.1021/acs.jctc.0c01135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Schirmer J.; Trofimov A. B. Intermediate state representation approach to physical properties of electronically excited molecules. J. Chem. Phys. 2004, 120, 11449. 10.1063/1.1752875. [DOI] [PubMed] [Google Scholar]
  80. Wormit M.; Rehn D. R.; Harbach P. H. P.; Wenzel J.; Krauter C. M.; Epifanovsky E.; Dreuw A. Investigating Excited Electronic States using the Algebraic Diagrammatic Construction (ADC) Approach of the Polarisation Propagator. Mol. Phys. 2014, 112, 774. 10.1080/00268976.2013.859313. [DOI] [Google Scholar]
  81. Véril M.; Scemama A.; Caffarel M.; Lipparini F.; Boggio-Pasqua M.; Jacquemin D.; Loos P.-F. QUESTDB: A database of highly accurate excitation energies for the electronic structure community. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2021, 11, e1517 10.1002/wcms.1517. [DOI] [Google Scholar]
  82. Mester D.; Kállay M. Combined density functional and algebraic-diagrammatic construction approach for accurate excitation energies and transition moments. J. Chem. Theory Comput. 2019, 15, 4440. 10.1021/acs.jctc.9b00391. [DOI] [PubMed] [Google Scholar]
  83. Grimme S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095. 10.1063/1.1569242. [DOI] [Google Scholar]
  84. Jung Y.; Lochan R. C.; Dutoi A. D.; Head-Gordon M. Scaled opposite-spin second order Møller–Plesset correlation energy: An economical electronic structure method. J. Chem. Phys. 2004, 121, 9793. 10.1063/1.1809602. [DOI] [PubMed] [Google Scholar]
  85. Kozuch S.; Gruzman D.; Martin J. M. L. DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction. J. Phys. Chem. C 2010, 114, 20801. 10.1021/jp1070852. [DOI] [Google Scholar]
  86. Rhee Y. M.; Head-Gordon M. Scaled Second-Order Perturbation Corrections to Configuration Interaction Singles: Efficient and Reliable Excitation Energy Methods. J. Phys. Chem. A 2007, 111, 5314. 10.1021/jp068409j. [DOI] [PubMed] [Google Scholar]
  87. Hellweg A.; Grün S. A.; Hättig C. Benchmarking the performance of spin-component scaled CC2 in ground and electronically excited states. Phys. Chem. Chem. Phys. 2008, 10, 4119. 10.1039/b803727b. [DOI] [PubMed] [Google Scholar]
  88. Winter N. O. C.; Hättig C. Scaled opposite-spin CC2 for ground and excited states with fourth order scaling computational costs. J. Chem. Phys. 2011, 134, 184101. 10.1063/1.3584177. [DOI] [PubMed] [Google Scholar]
  89. Casanova-Páez M.; Dardis M. B.; Goerigk L. ωB2PLYP and ωB2GPPLYP: The First Two Double-Hybrid Density Functionals with Long-Range Correction Optimized for Excitation Energies. J. Chem. Theory Comput. 2019, 15, 4735. 10.1021/acs.jctc.9b00013. [DOI] [PubMed] [Google Scholar]
  90. Mester D.; Kállay M. Spin-Scaled Range-Separated Double-Hybrid Density Functional Theory for Excited States. J. Chem. Theory Comput. 2021, 17, 4211. 10.1021/acs.jctc.1c00422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Mester D.; Kállay M. Accurate Spectral Properties within Double-Hybrid Density Functional Theory: A Spin-Scaled Range-Separated Second-Order Algebraic-Diagrammatic Construction-Based Approach. J. Chem. Theory Comput. 2022, 18, 865. 10.1021/acs.jctc.1c01100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Śmiga S.; Grabowski I. Spin-Component-Scaled ΔMP2 Parametrization: Toward a Simple and Reliable Method for Ionization Energies. J. Chem. Theory Comput. 2018, 14, 4780. 10.1021/acs.jctc.8b00638. [DOI] [PubMed] [Google Scholar]
  93. Pickup B. T.; Goscinski O. Direct calculation of ionization energies. Mol. Phys. 1973, 26, 1013. 10.1080/00268977300102261. [DOI] [Google Scholar]
  94. Vidal M. L.; Krylov A. I.; Coriani S. Dyson orbitals within the fc-CVS-EOM-CCSD framework: theory and application to X-ray photoelectron spectroscopy of ground and excited states. Phys. Chem. Chem. Phys. 2020, 22, 2693. 10.1039/C9CP03695D. [DOI] [PubMed] [Google Scholar]
  95. Díaz-Tinoco M.; Corzo H. H.; Pawłowski F.; Ortiz J. V. Do Dyson Orbitals resemble canonical Hartree–Fock orbitals?. Mol. Phys. 2019, 117, 2275. 10.1080/00268976.2018.1535142. [DOI] [Google Scholar]
  96. Ortiz J. V. Dyson-orbital concepts for description of electrons in molecules. J. Chem. Phys. 2020, 153, 070902. 10.1063/5.0016472. [DOI] [PubMed] [Google Scholar]
  97. Kállay M.; Nagy P. R.; Mester D.; Gyevi-Nagy L.; Csóka J.; Szabó P. B.; Rolik Z.; Samu G.; Csontos J.; Hégely B.; Ganyecz Á.; Ladjánszki I.; Szegedy L.; Ladóczki B.; Petrov K.; Farkas M.; Mezei P. D.; Horváth R. A.. Mrcc, a quantum chemical program suite. See https://www.mrcc.hu/ (accessed March 1, 2023).
  98. Butscher W.; Kammer W. E. Modification of Davidson’s Method for the Calculation of Eigenvalues and Eigenvectors of Large Real-Symmetric Matrices: “Root Homing Procedure”. J. Comput. Phys. 1976, 20, 313. 10.1016/0021-9991(76)90084-X. [DOI] [Google Scholar]
  99. Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. 10.1063/1.456153. [DOI] [Google Scholar]
  100. Woon D. E.; Dunning T. H. Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358. 10.1063/1.464303. [DOI] [Google Scholar]
  101. Kendall R. A.; Dunning T. H. Jr.; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796. 10.1063/1.462569. [DOI] [Google Scholar]
  102. Weigend F.; Köhn A.; Hättig C. Efficient use of the correlation consistent basis sets in resolution of the identity MP2 calculations. J. Chem. Phys. 2002, 116, 3175. 10.1063/1.1445115. [DOI] [Google Scholar]
  103. Weigend F.; Häser M.; Patzelt H.; Ahlrichs R. RI-MP2: optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143. 10.1016/S0009-2614(98)00862-8. [DOI] [Google Scholar]
  104. Weigend F. Hartree–Fock Exchange Fitting Basis Sets for H to Rn. J. Comput. Chem. 2008, 29, 167. 10.1002/jcc.20702. [DOI] [PubMed] [Google Scholar]
  105. Krack M.; Köster A. M. An adaptive numerical integrator for molecular integrals. J. Chem. Phys. 1998, 108, 3226. 10.1063/1.475719. [DOI] [Google Scholar]
  106. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  107. Becke A. D. Density-functional exchange-energy approximation with correct asymptotic-behavior. Phys. Rev. A 1988, 38, 3098. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  108. Lee C.; Yang W.; Parr R. G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  109. Perdew J. P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. 10.1103/PhysRevB.33.8822. [DOI] [PubMed] [Google Scholar]
  110. Becke A. D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554. 10.1063/1.475007. [DOI] [Google Scholar]
  111. Lehtola S.; Steigemann C.; Oliveira M. J. T.; Marques M. A. L. Recent developments in Libxc – A comprehensive library of functionals for density functional theory. SoftwareX 2018, 7, 1. 10.1016/j.softx.2017.11.002. [DOI] [Google Scholar]
  112. https://www.tddft.org/programs/libxc/ (accessed May 1, 2023).
  113. Kozuch S.; Martin J. M. L. DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104. 10.1039/c1cp22592h. [DOI] [PubMed] [Google Scholar]
  114. Chai J.-D.; Mao S.-P. Seeking for reliable double-hybrid density functionals without fitting parameters: The PBE0-2 functional. Chem. Phys. Lett. 2012, 538, 121. 10.1016/j.cplett.2012.04.045. [DOI] [Google Scholar]
  115. Alipour M. On the opposite-spin to same-spin ratio of absolute and interaction MP2 correlation energy in parameter-free spin-opposite-scaled double hybrids. Chem. Phys. Lett. 2017, 684, 423. 10.1016/j.cplett.2017.07.023. [DOI] [Google Scholar]
  116. Brémond É.; Sancho-García J. C.; Pérez-Jiménez Á. J.; Adamo C. Double-hybrid functionals from adiabatic-connection: The QIDH model. J. Chem. Phys. 2014, 141, 031101. 10.1063/1.4890314. [DOI] [PubMed] [Google Scholar]
  117. Karton A.; Tarnopolsky A.; Lamère J.-F.; Schatz G. C.; Martin J. M. L. Highly Accurate First-Principles Benchmark Data Sets for the Parametrization and Validation of Density Functional and Other Approximate Methods. Derivation of a Robust, Generally Applicable, Double-Hybrid Functional for Thermochemistry and Thermochemical Kinetics. J. Phys. Chem. A 2008, 112, 12868. 10.1021/jp801805p. [DOI] [PubMed] [Google Scholar]
  118. Chai J.-D.; Head-Gordon M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
  119. Yanai T.; Tew D. P.; Handy N. C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51. 10.1016/j.cplett.2004.06.011. [DOI] [Google Scholar]
  120. Perdew J. P.; Ernzerhof M.; Burke K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982. 10.1063/1.472933. [DOI] [Google Scholar]
  121. Liang J.; Feng X.; Hait D.; Head-Gordon M. Revisiting the Performance of Time-Dependent Density Functional Theory for Electronic Excitations: Assessment of 43 Popular and Recently Developed Functionals from Rungs One to Four. J. Chem. Theory Comput. 2022, 18, 3460. 10.1021/acs.jctc.2c00160. [DOI] [PubMed] [Google Scholar]
  122. Richard R. M.; Marshall M. S.; Dolgounitcheva O.; Ortiz J. V.; Brédas J.-L.; Marom N.; Sherrill C. D. Accurate Ionization Potentials and Electron Affinities of Acceptor Molecules I. Reference Data at the CCSD(T) Complete Basis Set Limit. J. Chem. Theory Comput. 2016, 12, 595. 10.1021/acs.jctc.5b00875. [DOI] [PubMed] [Google Scholar]
  123. Ranasinghe D. S.; Margraf J. T.; Perera A.; Bartlett R. J. Vertical valence ionization potential benchmarks from equation-of-motion coupled cluster theory and QTP functionals. J. Chem. Phys. 2019, 150, 074108. 10.1063/1.5084728. [DOI] [PubMed] [Google Scholar]
  124. Alag A. S.; Jelenfi D. P.; Tajti A.; Szalay P. G. Accurate Prediction of Vertical Ionization Potentials and Electron Affinities from Spin-Component Scaled CC2 and ADC(2) Models. J. Chem. Theory Comput. 2022, 18, 6794. 10.1021/acs.jctc.2c00624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  125. Śmiga S.; Siecińska S.; Grabowski I. From simple molecules to nanotubes. Reliable predictions of ionization potentials from the ΔMP2-SCS methods. New J. Phys. 2020, 22, 083084. 10.1088/1367-2630/abaa00. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct3c00363_si_001.xlsx (238KB, xlsx)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES