Characterizing Interfaces by Voronoi Tessellation

Abstract

The chemistry of interfaces differs markedly from that of the bulk. Calculation of interfacial properties depends strongly on the definition of the interface, which can lead to ambiguous results that vary between studies. There is a need for a method that can explicitly define the interfaces and boundaries in molecular systems. Voronoi tessellation offers an attractive solution to this problem through its ability to determine neighbors among specified groups of atoms. Here we discuss three cases where Voronoi tessellation combined with modeling of vibrational sum frequency generation (SFG) spectroscopy yields relevant insights: the breakdown of the air-water interface into clear and intuitive molecular layers, the study of the hydration shell in biological systems, and the acceleration of difficult spectral calculations where intermolecular vibrational couplings dominate. The utility of Voronoi tessellation has broad applications that extend beyond any single type of spectroscopy or system.

TOC graphic

Interfaces play a central role in biological, chemical, and industrial processes. Most biological processes occur in aqueous environments, and the interface between water and the protein or nucleic acid often plays an important structural and functional role.^1–3 Moreover, electrochemical processes critical to energy conversion, such as carbon dioxide reduction and the oxygen evolution and oxygen reduction reactions, occur at metal-electrolyte interfaces.^4–6 The air-water interface is particularly important in atmospheric chemistry that occurs on the surface of water droplets.^7–8 Thus, developing both experimental and computational methods for probing interfaces has widespread applications.

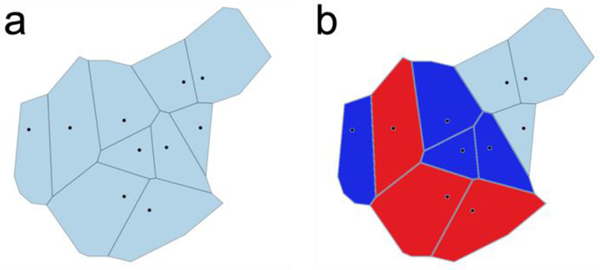
One of the central challenges in vibrational spectroscopic approaches aimed at probing interfaces is identifying the sources of the vibrational signals, which is often achieved through simulation. Analysis of the simulations typically requires the dissection of the system into interfacial regions and boundaries. Although distance-based cutoffs are commonly used for this purpose, the cutoff definition can be arbitrary and therefore yield inconsistent results. Voronoi tessellation defines interfaces and boundaries unambiguously by dividing a space containing a set of points into cells (Figure 1a) and determining the neighbors of each cell (Figure 1b).⁹ A Voronoi cell consists of the area that is closer to its central point than to any other point. Once a Voronoi tessellation is computed, it becomes trivial to identify nearest neighbors of any set of points. Voronoi tessellation offers a computational scalpel that allows the atomic-level dissection of complex systems to help identify the sources of spectroscopic features.

Figure 1.

a) A two-dimensional Voronoi tessellation, where each cell consists of the area closer to the central point than to any other points. b) Finding neighbors of a set of points is straightforward once the Voronoi tessellation has been made. Here, the dark blue cells are the neighbors of the red cells.

Vibrational sum frequency generation (SFG) spectroscopy is a second-order nonlinear spectroscopy that is surface-selective and thus is an excellent technique for probing both achiral and chiral interfacial systems.^10–28 This technique involves overlapping infrared (IR) and visible pulses in space and time on the sample and measuring the sum frequency response. By manipulating the polarization of the IR and visible beams and that of the detector, individual elements or a subset of the 27 elements of the susceptibility tensor ${\chi }_{IJK}^{(2)}$ can be isolated. Our group performs chirality-selective SFG (chiral SFG) using the polarization that isolates the element ${\chi }_{ZYX}^{(2)}$, which is sensitive to chirality at interfaces, including solvent chirality induced by a chiral solute.^29–30 Our group also performs conventional SFG (or achiral SFG) using the polarization that isolates the element ${\chi }_{YYZ}^{(2)}$, which is sensitive to interfaces but not chirality.³¹ The SFG process is coherent, which allows for the extraction of the imaginary component of the response with heterodyne detection.^{24, 26–27, 32–33} In achiral SFG, the sign of the peaks corresponds to the z-direction orientation of corresponding dipoles, whereas in chiral SFG, the sign of the phase has no clear meaning. Our group has used chiral SFG, in conjunction with molecular dynamics (MD) simulations and spectral calculations using electrostatic frequency maps,³⁴ to guide the interpretation of these spectra and study various biological systems.^{20–26, 31, 34–37}

Herein, we combine Voronoi tessellation with computational modeling of SFG to reveal significant atomic-level properties of interfacial systems. We illustrate the power of this strategy for three diverse applications. First, we show how Voronoi tessellation can be used to divide the water at an air-water interface into well-defined layers, which then allows the calculation of the SFG response from each individual layer. This type of analysis provides insight into the hydrogen-bonding interactions between layers at the interface. Second, we show how Voronoi tessellation can be used to define the first hydration shell around a protein at an air-water interface, and further dissect the first hydration shell into water molecules near the protein backbone versus those near the sidechains. Simulation of the chiral SFG response from each subset of water provides insight into the different hydrogen-bonding interactions between the protein and water and assists in the interpretation of the experimental data. Third, we show how the identification of the first hydration shell around a biomolecule can be used to speed up simulations of chiral SFG spectra without a significant loss of accuracy.

Although the pure air-water interface has been studied extensively, it is challenging to divide the interface into well-defined layers to calculate the vibrational response of each layer.^{10, 12, 17, 19, 38–48} In some cases, SFG calculations of the air-water interface contradict each other due to subtle differences in definitions of interfacial layers.^{46, 49} The popular instantaneous liquid interface method⁵⁰ relies on coarse-graining of the atomic density of the system, which involves arbitrary parameters such as coarse-graining length and grid size. By contrast, Voronoi tessellation defines layers unambiguously regardless of their composition. We use this approach to computationally divide the interfacial water into well-defined molecular layers (see Figure 2a and Supporting Information (SI)). In brief, we first add virtual points above the surface, construct a Voronoi tessellation with a cell for each atom and virtual point, and then identify the atom neighbors of the virtual points. If any one of a water molecule’s atoms is a neighbor, the whole molecule is included in the first layer. We repeat the procedure for subsequent layers using the previous layer’s atoms instead of the virtual points. We then calculate the achiral SFG response of each layer (Figure 2b) using two different water models, SPC/E and TIP4P-Ew.^51,52 Future layer-by-layer SFG simulations might use a higher level of theory (i.e., ab initio MD), following previous work,^{38, 53–54} but this will most likely only allow convergence of the top few layers’ spectra due to sampling limitations (i.e., ab initio MD trajectories cannot be propagated for enough time to converge very weak signals). To obtain the necessary copious sampling, we use classical force fields for this study.

Figure 2.

a) Water surface separated into layers (layer 1 – red, layer 2 – blue, layer 3 – orange, layer 4 – magenta) using Voronoi tessellation neighbor analysis. b) Computed achiral SFG spectra using two different water models, SPC/E (gray) and TIP4P-Ew (colors corresponding to those in part a). c) Analysis of hydrogen bonds and molecule diffusion between water layers for SPC/E (purple) and TIP4P-Ew (orange) systems. The arrows indicate either donation of a hydrogen bond from one layer to the adjacent layer or the transfer of water molecules from one layer to the adjacent layer over 1 ps. Values are shown as mean ± standard error.

We find that the top layer (layer 1, Figure 2a, red) produces most of the observed signal (Figure 2b, red), as expected from previous analyses.⁴⁶ There is a positive peak at high frequency (~3700 cm⁻¹) corresponding to free OH groups pointing up into the vacuum and a negative peak at lower frequency (~3450 cm⁻¹) corresponding to OH groups pointing down and interacting with the lower layer of water. Because red-shifting of the OH stretch away from ~3700 cm⁻¹ is associated with stronger hydrogen bonding, this negative peak corresponds to hydrogen bonded OH groups. However, the SFG response of layer 2 (Figure 2a, blue) is less obvious. Its lineshape is inverted compared to that of layer 1 (Figure 2b, red versus blue), with the strong hydrogen bonds being donated up into layer 1 rather than down into layer 3 (Figure 2a, orange). This indicates that layer 2 and layer 1 have a particularly strong attraction compared to those of other pairs of layers. Analysis of hydrogen bonds between the layers (Figure 2c) reveals that for both water models, the hydrogen bond length is 2.88 Å between all layers except that the water molecules donating hydrogen bonds from layer 2 into layer 1 have shorter hydrogen bonds of length 2.86 Å with a hydrogen bond angle slightly closer to the ideal 180°. This stronger hydrogen bonding corresponds to the water molecules pointing up from layer 2 into layer 1. This analysis demonstrates the exquisite sensitivity of SFG to the substructure of the interface as well as the utility of Voronoi tessellation in unraveling subtle molecular features when combined with SFG modeling. We note that our SFG results for the first few layers are similar to those obtained by Kaliannan et al. using a probe-based layer identification method.³⁹ An advantage of Voronoi tessellation is that once the tessellation is done for a given configuration, identifying any number of layers is computationally trivial, as there is no need to probe each layer individually.

Although the SFG responses of layer 1 and layer 2 (i.e., the top ~5 Å) are significant, those of the lower layers are very small (Figure 2b). However, layer 3 (Figure 2a, orange) has a very well-converged SFG response that is very similar to that of layer 2 – molecules with OH groups pointing up have stronger hydrogen-bonding interactions. This layer extends ~10 Å below the surface. Although our hydrogen bond analysis (Figure 2c) was unable to pick up any significant differences between molecules pointing up and down in this layer, the SFG response indicates a subtle asymmetry in this layer. This suggests that the orientations of water molecules in layer 3 are still influenced by the interface, however slightly. Even though we averaged over 10,000,000 frames and 100 ns of simulation, the layer 4 spectra (Figure 2b, magenta) are poorly converged. However, both water models show a lineshape curiously similar to that of layer 1 – molecules facing up have very slightly weaker hydrogen bonds than molecules facing down. Together all these results suggest a model where truly bulk behavior is not reached even ~16 Å below the surface, contrary to past suggestions that only the first several Å are important.^55–58

Although the SFG signal mostly originates within the first few water layers,⁴⁶ some properties converge much less quickly. In particular, we calculated the average number of water molecules that move between adjacent layers (normalized per water molecule) over 1 ps and found that the value does not converge to the bulk value even four layers down (Figure 2c). The rate of interlayer water transfer increases with each subsequent layer, suggesting that the interface has slower diffusion in the z-direction than the bulk and that this property does not rapidly approach a bulk value. This implies that water molecules that are affected by the surface may not only include the top few layers but may also include deeper regions as well. Voronoi tessellation has enabled us to precisely define molecular layers and uncover hidden properties of the interface and reveals that the definition of the interface is dependent on the property used to define it.

In addition to defining molecular layers at interfaces, Voronoi tessellation can also unambiguously define the hydration shell of a biomolecule.⁵⁹ Our group has used Voronoi tessellation to define the first and second hydration shells around the model system LK₇β, an amphiphilic peptide that folds into antiparallel β-sheets at the air-water interface, which makes it an ideal benchmark system for SFG studies.^{27, 37} This system consists of leucine residues that point into the air and positively charged lysine residues that point into the water (Figure 3). LE₇β contains negatively charged glutamate residues instead of lysine residues, but it is otherwise very similar to LK₇β. We model each protein as a five-stranded antiparallel β-sheet at the vacuum-water interface. Together, Voronoi tessellation and chiral SFG reveal surprising differences between the hydration shells of the two similar proteins.

Figure 3.

a) Structure and chemical properties of leucine (L), lysine (K), and glutamate (E). b) LK₇β and LE₇β peptides. c) These peptides form antiparallel β-sheets at the air-water interface, where polar residues lysine (K) or glutamate (E) point into the solvent while hydrophobic residues leucine (L) point into the air; top view of aqueous LK₇β. d) and side view of aqueous LK₇β.

In a previous study, we used Voronoi tessellation to identify the first solvation shell but then used distance cutoffs to separate water molecules interacting with the backbone from those interacting with the sidechains. This involved rather convoluted selection criteria (see ref 27, SI) that ultimately did not perfectly remove the overlap between subsets, complicating spectral interpretation of the backbone- and sidechain-associated water molecule contributions. Here, we greatly simplify the selection by defining “backbone water” as those molecules that are direct neighbors of backbone atoms and “sidechain water” as those that are direct neighbors of the ends of the sidechains (the NH₃⁺ group in LK₇β; the COO^– group in LE₇β) and are not also neighbors of the backbone (Figure 4a). Voronoi tessellation enables precise yet simple partitioning of the first hydration shell into components. The chiral SFG response of these subsets can then be calculated to reveal the components of the total SFG spectrum.

Figure 4.

(a) Voronoi tessellation-based selections of water molecules near the backbone (red) and near sidechains (blue) of LK₇β (transparent yellow). (b) Computed first hydration shell OH-stretch response for LK₇β (black) and LE₇β (red). (c) Computed backbone-associated water OH-stretch response for LK₇β and LE₇β. (d) Computed sidechain-associated water OH-stretch response for LK₇β and LE₇β.

We have previously shown that the main NH stretch peak in the chiral SFG spectrum of LE₇β is blue-shifted compared to the analogous peak in LK₇β. We argued that this shift is due to significantly fewer backbone hydrogen bonds in LE₇β compared to LK₇β, which indicates weaker inter-strand hydrogen-bonding interactions in LE₇β, but we did not analyze the OH stretch components of the spectrum.³⁷ Figures 4b and 4c show that the first hydration shell and backbone water responses of LE₇β are very different from those of LK₇β, even though the systems appear similar. The OH stretch response of LE₇β is both much smaller and somewhat blue-shifted compared to that of LK₇β. The blue shift might indicate that the hydration shell of LE₇β is less strongly bound compared to the hydration shell of LK₇β. However, hydrogen bond analysis reveals that this is not the case. Instead, protein-water hydrogen bonds are actually somewhat stronger in LE₇β compared to LK₇β (donor-acceptor distances of 2.74 ± 0.0002 Å vs. 2.87 ± 0.0002 Å and angles of 164.58 ± 0.0083° vs. 162.56 ± 0.0110°, mean ± standard error). This analysis suggests that the key variable in determining the chiral OH stretch response and the integrity of the first hydration shell is the stability of the protein structure rather than the strength of the interaction between the protein and the surrounding water. LK₇β forms a more stable antiparallel β-sheet structure,³⁷ and therefore its hydration shell maintains a more rigid chiral structure. The blue shift and smaller response of LE₇β compared to LK₇β illustrates differential chiral induction – a different degree of imprinting of chirality on achiral solvent. Comparison of the two systems suggests that hydration water spectra can be used to infer relative biomolecule stability in some cases. In addition, we find that the backbone-associated water molecules contribute most of the lineshape in both systems (Figure 4c), and the sidechain responses (Figure 4d) are quite small. This observation is consistent with our previous work, where we found that water molecules hydrogen bonded to carbonyl groups on the backbone were significant contributors to the chiral SFG response of the first hydration shell, especially on a per-water-molecule basis.²⁷

In addition to revealing the structure of molecular systems, Voronoi tessellation can also speed up the calculation of chiral SFG spectra. The SFG calculations presented thus far have taken advantage of an approximation where intermolecular couplings between OH groups are neglected. This approximation allows simple separation of water molecule subsets and makes the exciton Hamiltonian matrix block-diagonal and thus trivial to diagonalize.^27,60–63 However, in certain cases, intermolecular couplings are crucial to chiral SFG spectra, and these make the Hamiltonian expensive to diagonalize. In particular, our previous work showed that intermolecular coupling is critical to the modeling of the combined NH/OH stretch chiral SFG response of LK₇β.³⁷ If intermolecular coupling is neglected, a downward-pointing peak appears that is not found in the experimental spectrum (Figure 5a). Our previous work also showed that almost all of the OH stretch signal and the most relevant NH/OH couplings arise between the biomolecule and the first hydration shell.²⁷ Here we obtain the first hydration shell by Voronoi tessellation, as discussed above, and then only consider the protein and the first hydration shell in the exciton Hamiltonian to speed up the calculation.³⁷

Figure 5.

a) NH stretch / OH stretch chiral SFG spectra of LK₇β and surrounding water, showing the modest effect of the first-hydration-shell approximation and strong effect of excluding intermolecular couplings between NH and OH groups. b) Speedup factor for the first-hydration-shell method over full-system calculation for molecular systems of various sizes.

Figure 5a shows the result of the first-hydration-shell approximation along with the full-system calculation for LK₇β. All features found in the full-system spectrum are present in the first-hydration-shell spectrum. The agreement with experiment is good whether or not the approximation is applied, except for the low-frequency negative peak at ~3150 cm⁻¹, which is missing in all the calculated spectra and is a focus of ongoing efforts by our group.³⁷

Figure 5b shows the increasing speedup of including only the first hydration shell as a function of system size. Using Voronoi tessellation to unambiguously define the first hydration shell can significantly accelerate prohibitively expensive spectral calculations and will enable modeling of vibrational spectra of large biological systems in the future without a significant sacrifice in accuracy. Modeling chiral SFG spectra of large systems will enable us to probe water-protein interactions of amyloids, antibodies, and other biologically relevant systems and learn how surrounding water molecules shape, and are shaped by, these systems.

We have shown a diverse set of three situations where Voronoi tessellation combined with SFG modeling yields insights. First, we demonstrated that Voronoi tessellation allows the dissection of the air-water interface at a high level of detail, yielding new findings about interface structure and thickness. We then showed that Voronoi tessellation enables detailed analysis of the differences between the first hydration shells of closely related protein systems. Finally, we used Voronoi tessellation and the knowledge that chiral SFG is largely selective to the first hydration shell²⁷ to greatly simplify and speed up the calculation of vibrational spectra of highly coupled condensed-phase systems. Although we restricted our study to SFG, the Voronoi tessellation approaches developed here can potentially be applicable in a variety of molecular contexts, for example in the analysis of surface-selective attenuated total reflectance IR spectroscopy (ATR-IR) experiments, protein-protein interactions, and biomolecule-lipid interactions. These approaches will also be applicable to the SFG study of charged aqueous interfaces relevant to electrocatalysis. Altogether, our findings demonstrate the remarkable power of combining Voronoi tessellation with modeling of vibrational spectroscopy.