Abstract
A widely mentioned but not experimentally confirmed view (known as the ‘criticality hypothesis’) argues that biological swarm systems gain optimal responsiveness to perturbations and information processing capabilities by operating near the critical state where an ordered-to-disordered state transition occurs. However, various factors can induce the ordered–disordered transition, and the explicit relationship between these factors and the criticality is still unclear. Here, we present an experimental validation for the criticality hypothesis by employing real programmable swarm-robotic systems (up to 50 robots) governed by Vicsek-like interactions, subject to time-varying stimulus-response and hazard avoidance. We find that (i) not all ordered–disordered motion transitions correspond to the functional advantages for groups; (ii) collective response of groups is maximized near the critical state induced by alignment weight or scale rather than noise and other non-alignment factors; and (iii) those non-alignment factors act to highlight the functional advantages of alignment-induced criticality. These results suggest that the adjustability of velocity or directional coupling between individuals plays an essential role in the acquisition of maximizing collective response by criticality. Our results contribute to understanding the adjustment strategies of animal interactions from a perspective of criticality and provide insights into the design and control of swarm robotics.
Keywords: criticality, collective response, swarm robots, self-organization, alignment, ordered–disordered motion transition
1. Introduction
To survive in the crisis-ridden environment, organisms must adapt swiftly and respond precisely to diverse, unpredictable and ever-changing situations. Recent empirical studies have found that numerous biological systems tend to operate near the dynamical critical state of ordered and disordered to gain adaptive advantages in dealing with their complex environments (i.e. the ‘criticality hypothesis’) [1–4]. The related biological systems include the brain and cortex [5–7], retinal neurons [8], gene regulation networks [9], bacterial clusters [10], social amoebas [11], ant colonies [12,13], midge swarms [14], sheep herds [15], bird flocks [16–18] and fish schools [19–21]. In principle, criticality is essential to biological systems, and it provides a delicate balance between two unrealistic tendencies [22,23]: if a system is too random, it will not be able to transfer information and reproduce stability; if it is too ordered, it will not be able to adapt to perturbations quickly. Just as confirmed by extensive evidences of previous studies, the criticality can confer a wide range of adaptive advantages to biological systems, such as optimal information representation and processing [3,4,24,25], maximal sensory dynamic range [26,27], optimal sensitivity to perturbations [28,29], maximal functional diversity [30] and emergence of collective intelligence [31].
The fascinating functional benefits of criticality have been explored by various theoretical models [24,25,28,29,32]. However, it still remains a challenge to experimentally test or validate the criticality hypothesis in real animal groups [2]. This is partially due to the fact that the ‘real image’ of animal behaviours is very hard to reveal or even impossible to know explicitly, especially when their actions have certain randomness due to environmental disturbances. The second challenge lies in that we cannot arbitrarily analyse animal groups through parameter sensitivity analysis, i.e. analysing the features associated with the critical state by fine-tuning the individual-level interacting elements and observing the changes in group-level attributes they produce. A further challenge is that the physical characteristics often used as criticality’s evidence, such as power-law scaling [14] and susceptibility [29], are phenomenological, and they may have different origins [3,28,33,34]. It is very difficult to directly access the functional evidence of criticality in real animal groups.
Thankfully, programmable swarm-robotic systems provide us with an ideal test-bed to validate the criticality hypothesis [35]. By arbitrarily customizing the interaction rules or strategies of inter-robots (which can be inferred from animal groups [36,37] or made up from theoretical models of our interests [38,39]) and programming to change the behavioural strength or scale of each robot, it is feasible to control these artificial swarm systems to reach or move away from a critical state. Consequently, based on the on-board (local) and global data acquisition systems, verifying the functional benefits of criticality associated with certain interaction mechanisms or behavioural rules is very convenient. Incidentally, computer simulations are now widely used to study collective behaviour [25,29,32,38–43], making modelling easier and faster, especially for large-scale groups. However, due to certain environmental factors and physical processes that cannot be modelled accurately or require enormous modelling effort (e.g. rocky terrain, air turbulence, inelastic contact, pheromone diffusion with wind, energy consumption, etc.), computer simulations typically only consider relatively simple individual interactions and idealized environments. Alternatively, since all of these physical features are inherently available for physical robotic systems, and no additional computational cost is required, swarm robots can go beyond numerical simulations and help us to study the dynamics and properties of biological swarms in more real-world environments. Furthermore, in the field of swarm robotics, computational simulations serve more as auxiliary tools, while physical robotic experiments are indispensable. In short, swarm robots can provide more valuable insights into biological swarms and swarm robotics.
Here, we focus on the criticality hypothesis presented in coordinated collective motion of animals [16–21]. Most claims on the benefits of criticality in these self-organized systems are speculative [19,25,44] and have not been validated with rigorous testing [28]. This leads to vague and general claims, such as a critical advantage is obtained when the flock is at the edge of chaos. It is true in principle, but fails to provide an explicit relationship between individual’s behavioural characteristics and group’s functional advantages. Although previous works have revealed that the disordered–ordered transition of collective motion is universal and has many origins [19,38,41,45–49], the explicit relationship between the phase transitions and group functions is still lacking, particularly rare efforts have been made by using physical experiments.
This work aims to explore the above ambiguous relationship by means of real swarm-robotic experiments. Specifically, we are concentrated on the following questions: Which inducer of criticality contributes to maximizing the collective response of groups? How and to what extent do different behavioural factors of individuals impact the group benefits of criticality in collective response? To this end, our swarm-robotic experiments consider not only the spontaneous collective motion, but also the collective response to external stimuli and the collective evasion of predators. We directly focus on the functional characteristics of groups, such as temporal efficiency, response accuracy and spatial configurations of robotic swarms. This helps us to avoid being trapped in the multiple-origins issue when using other phenomenological evidence of criticality. We found that the factors that can cause the criticality with group functional benefits are specialized rather than universal. Specifically, the criticality caused by the strength and scale of alignment is the only way to maximize the collective response of groups. At the same time, the other non-alignment factors, such as noise, can enhance this functional advantage of alignment-induced criticality. Therefore, whether a swarm system has gained some adaptive advantages due to being in a critical state cannot be solely determined by the phenomenological characteristic, i.e. at the edge of chaos. From an engineering view, our results provide direct insight into operating an artificial swarm system, say, a swarm of drones, near the critical state.
2. The swarm-robotic system
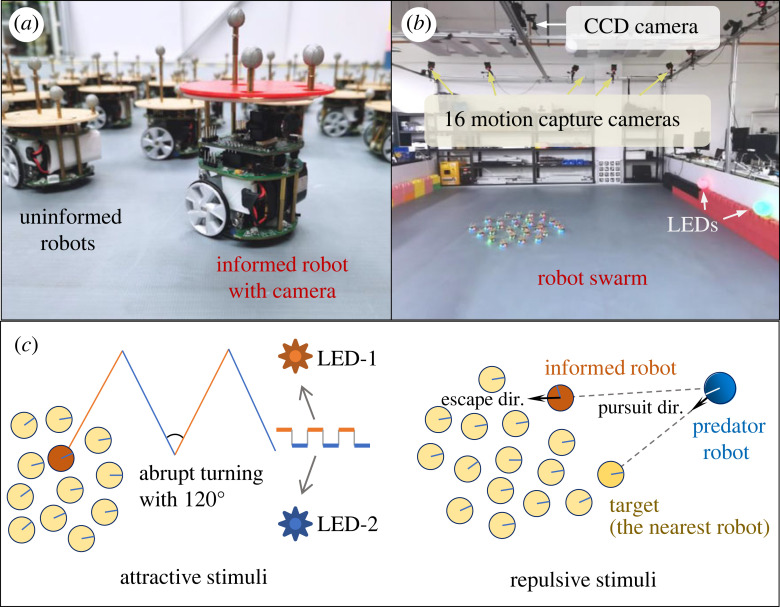
The SwarmBang robots, see figure 1a, are employed in our experiments to investigate the criticality hypothesis. These two-wheeled differential-driven miniature mobile robots are designed specifically to study bioinspired collective behaviours. See appendix A for more details.
Figure 1.
The swarm-robotic system and experimental set-up. (a) The SwarmBang robots. The informed robot with a camera can perceive ambient stimuli, whereas the other uninformed robots are unaware of the stimuli. (b) The experiment arena uses motion capture system to track robots’ position and heading, and a top-view CCD camera to record the trial video. (c) Illustration of the external stimuli. For the attractive stimuli, two different coloured LED lights are installed at the arena edge to attract the informed robot. They alternately light up in a 200-step cycle, guiding the informed robot to perform abrupt turning actions consecutively. For the repulsive stimuli, a faster-moving robot is introduced as a predator to attack the swarm robots.
The self-organizing rules of SwarmBang robots are designed according to some widely accepted modelling principles in group-living animals: (i) individuals tend to move away from too close neighbours to maintain their personal space [36,39,40]; (ii) group cohesion arises from the attractive effect of distant neighbours [36,40,50]; (iii) individuals tend to align their orientation with that of nearby neighbours [38,41,50]; and (iv) when a group is stimulated by an external perturbation, an individual makes a biased motion to get closer to or run away from the stimulus source [42].
Consider a group of N SwarmBang robots moving on a flat, obstacle-free ground, as shown in figure 1b. Each robot i with a position vector and a unit direction vector attempts to maintain a constant speed v0. The decision-making process of each robot is discrete, with an action cycle of τ seconds. The social interaction term is calculated as follows in each action cycle:
| 2.1 |
where is the distance between two robots at time t; wali and Dali represent the weight and spatial scale of velocity-alignment behaviour, respectively. The repulsion–attraction behaviour between a pair of robots is formulated as
| 2.2 |
where wrep and Drep (watt and Datt) represent the strength and spatial scale of the repulsion (attraction) behaviour, respectively. To establish a distance-regulating social force, the weights and scales, i.e. Drep ≪ Datt and wrep ≫ watt, are used to achieve ‘short-range repulsion and long-range attraction’ among robots.
The social interaction term is then used to determine the desired motion direction of robot in the next action cycle as
| 2.3 |
where αsoc ∈ [0, 1] denotes the social level of individuals to characterize the evidence that animals may adjust their attention to their neighbours to meet the circumstances or behavioural context [40]. In this manner, the robot devotes some of its attention (αsoc) to the motion of its neighbours while devoting the remaining (1 − αsoc) to its own motion. In other words, it attempts to strike a balance between its own motion direction and the direction towards and alignment with its neighbours. Extremely, a robot moves in its current direction while disregarding its neighbours’ motion as αsoc = 0; it follows its neighbours’ motion completely as αsoc = 1, implying that its behaviour is without inertia or memory. ηmΓi models the randomness of individuals’ motion (motion noise) caused by uneven ground or inaccurate internal decisions (arising from the perceptual and/or execution errors) with the intensity ηm ∈ [0, 1] and the unit uniform noise Γi ∼ U(−0.5, 0.5).
The external stimulus (i.e. environmental perturbation) is represented by a time-varying unit vector . We choose one robot g ∈ [1, …, N] as the ‘informed robot’, assuming that its attention is fully attracted by the external stimuli, i.e. its desired direction . Other robots are naive and unaware of external perturbation. Thus, a local stimulus is imposed into the robotic swarm. Two forms of perturbation are considered in our experiments to mimic the attractive effect of food sources and the repulsive effect of predators in the natural world (see figure 1c and the next section for more details).
Then, the desired direction of motion and translational velocity v0 are sent to SwarmBang robots to regulate their motions. See appendix A for details on the experimental set-up.
With the above behavioural rules of swarm robots, five interactional factors are programmed into the controlling cycle of each robot. That is, the noise intensity ηm, the alignment weight wali, the alignment scale Dali, the social level αsoc and the action cycle τ. These factors fall into two categories, namely, alignment factors (i.e. wali, Dali) and non-alignment factors (i.e. ηm, αsoc and τ). If not specified otherwise, the number of robots in our experiments is N = 30, and the default parameters are v0 = 15 mm s−1, τ = 0.2 s, watt = 1, Datt = 400, wrep = 20, Drep = 100, ηm = 0. See electronic supplementary material, table S1, for all parameters used in our swarm-robotic experiment.
At the beginning of the experiment, swarm robots are arranged in a circular area, with random orientations and an inter-robot spacing of approximately one or two body-lengths, to facilitate their initial interactions. The informed robot is placed at the centre (side) of the robotic swarm to introduce the attractive (repulsive) stimuli.
3. Experimental results
3.1. Ordered–disordered transition of collective motion can be induced by various factors
A non-equilibrium phase transition that separates the disordered state from the ordered state is frequently observed in the Vicsek model [38] and its variants [51]. We will first investigate the spontaneous collective motion using real swarm robots and increasing our understanding of some interactional factors that have not been explored efficiently before. We use the polarization, ψ(t), to quantify the instantaneous orientational order of the robotic swarm, the flocking elapsed time, Tord, to quantify the time it takes to form an ordered motion from a disordered configuration, and the nearest neighbour distance of individual, nndi(t), to characterize the relative spatial configuration between robots.
| 3.1 |
| 3.2 |
| 3.3 |
Here, ψ ∈ [0, 1], ψ = 1 represents that all robots move in the same direction while they move randomly when ψ ≈ 0. θord is a threshold for determining whether robots’ headings reach a common direction (we let θord = 0.9 in all trials). Since the spatial distribution of our robotic swarm is generally homogeneous, for simplicity, we employ the minimum nearest neighbour distance, dnn(t) = min i∈[1, … N] nndi(t), to compressively indicate its spatial feature in the subsequent analysis. A smaller value of dnn leads to a greater risk of inter-robot collisions (the minimum spacing for our robots is approx. 80 mm).
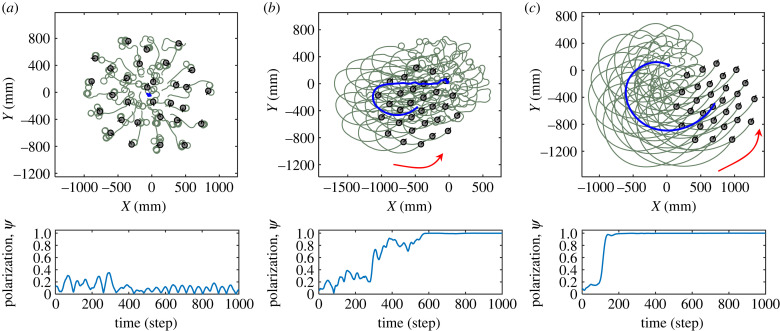
Figure 2 presents three typical collective motion patterns that spontaneously emerge from our robotic swarms. It is seen that, with a weak or strong alignment weight, the swarm robots tend to perform swarming or flocking behaviour. As shown in figure 2a, the robots move in random directions with collisions, which can be regarded as disordered collective motion. In figure 2c, the robots aggregate and move in a common direction, suggesting that an ordered collective motion emerges. When we gradually increase the alignment weight from the disordered state to the ordered state, a critical condition that separates the disordered and ordered states is observed, as shown in figure 2b. In such cases, each robot’s moving direction is aligned with slight fluctuations, while the whole group occasionally takes random turnings spontaneously.
Figure 2.
Three typical trials of spontaneous collective motion in swarm-robotic experiments. (a) Disordered collective motion with weak alignment weight (wali = 15). (b) Ordered collective motion close to the critical state (wali = 30). (c) Ordered collective motion with strong alignment weight (wali = 100). The thick blue line indicates the trajectory of robotic swarm’s centre. See electronic supplementary material, video S1, for more details.
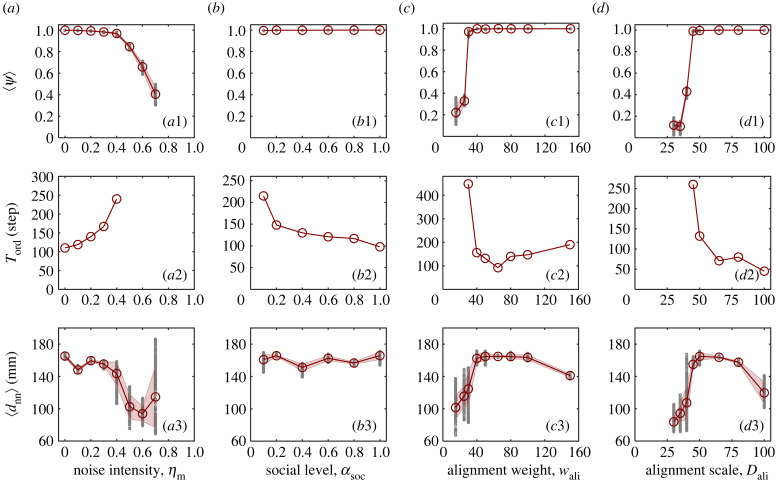
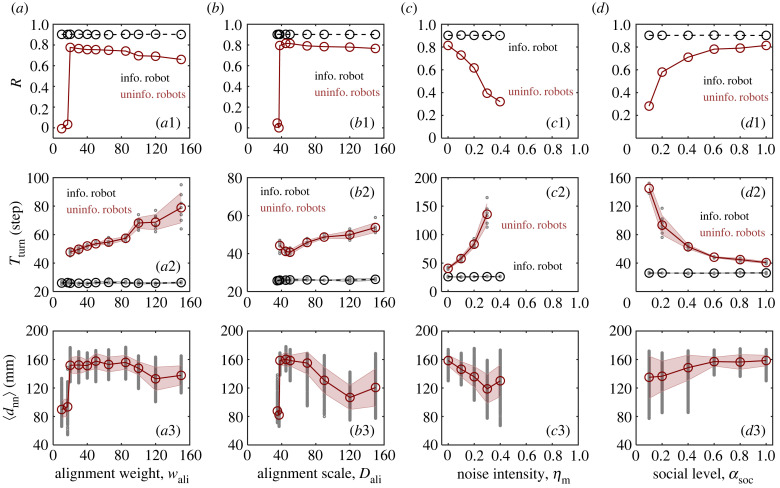
We next investigate the impacts of noise intensity (ηm), social level (αsoc), alignment weight (wali) and alignment scale (Dali) on the spontaneous collective motion. As shown in figure 3, all these factors can cause a disordered–ordered motion transition. Specifically, increasing the noise intensity will gradually disturb the orderliness of collective motion (figure 3a1). By contrast, the group will lose its orderliness abruptly as the decrease of the social level (figure 3b1), alignment scale (figure 3c1) and alignment weight (figure 3d1). According to our experimental data, with specific settings of ηm = 0, αsoc = 1, wali = 50 and Dali = 50, the intervals of each parameter leading to an ordered collective motion are as follows: , , and . Notably, at low social level (), disordered motion manifests as a weak aggregation of robots spreading in all directions (data not shown in figure 3b1). This is because robots are excessively independent, as opposed to the highly coupled chaotic collective motion in figure 2a.
Figure 3.
Experimental results on spontaneous collective motion. (a) Noise intensity ηm, (b) social level αsoc, (c) alignment weight wali, (d) alignment scale Dali. (a1,b1,c1,d1) The group polarization 〈ψ〉, (a2,b2,c2,d2) the flocking elapsed time Tord and (a3,b3,c3,d3) the minimum nearest neighbour distance 〈dnn〉 as a function of these factors, respectively. 〈·〉 symbolizes the average over time; 〈ψ〉 and 〈dnn〉 are averaged over the last 50 and 200 steps, respectively. The corresponding time-evolving curves of ψ(t) and dnn(t) are presented in electronic supplementary material, figure S2.
According to our experimental results, an empirically continuous, i.e. second-order, phase transition is induced by noise (figure 3a1), which agrees with previously reported noise-induced phase transitions, in both numerical simulations [38,45] and mean-field approximations [51]. Instead, an empirically discontinuous, i.e. first-order, phase transition is induced by the alignment weight and scale, respectively (figure 3c1,d1). The bistable dynamics is also seen when the values of wali and Dali are close to the critical points; that is, given identical parameters, the robotic swarms display either ordered or disordered collective motion (see electronic supplementary material, figure S1). It should be noted that the goal of this subsection is not to exactly figure out the nature of these phase transitions, but rather to get a general sense to guide the subsequent analysis.
For temporal features, we observe from figure 3a2,b2,c2,d2 that the decrement of ψ is accompanied by an increment of Tord, and the critical slow-down effect [52] becomes more significant near the transition point. It suggests that as the disordered–ordered motion transition approaches, robotic swarms will require more time to reach a consensus direction from a random state. In terms of spatial features, figure 3c3,d3 shows that the maximum value of dnn occurs just above the transition point with regard to the alignment weight and scale, implying that the swarm robots may achieve optimal safety near the critical value of alignment.
3.2. Collective response is maximized by alignment-induced criticality rather than others
This subsection focuses on the issue of whether the collective response to local stimuli is maximized when robotic swarms work near the critical point, as pointed (predicted) by the criticality hypothesis. As illustrated in figure 1a, an informed robot is programmed to periodically make abrupt turnings of . These turnings are seen as local-attractive stimuli that affect the movement of the whole robotic swarm. To quantify the instantaneous quality of robotic swarm’s response to the local stimuli [43], we define the group response accuracy, acc(t), as follows:
| 3.4 |
where is the time-varying signal that guides the informed robot g, and is the orientation of the ith robot. We have acc(t) ∈ [ − 1, 1], such that the robotic swarm is able to collectively and precisely respond to the stimuli when acc(t) → 1.
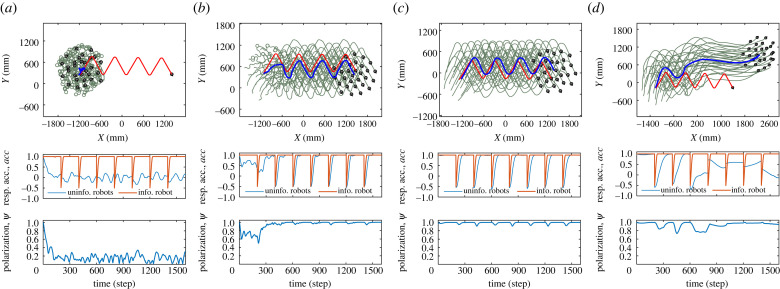
Figure 4 presents the trajectories of robots responding to the periodic stimuli with wali = [10, 20, 150], respectively. It is seen that when wali = 10, the robotic swarm is unable to form ordered motion, its response to stimuli is negligible (figure 4a). When wali = 20, the robotic swarm works near the critical state. The robots successfully respond to the periodic stimuli and make synchronized turnings (figure 4b). However, for wali = 150, compared to wali = 20, the robotic swarm can form ordered motion more quickly, but the performance of the collective turning is slower and has less accuracy (figure 4c). Furthermore, as the social level of robots decreases from 0.5 to 0.2, the response accuracy of group becomes worse (figure 4d). Note that the angular speed of our robot is limited, so the informed robot’s response accuracy acc(t) lags in converging to 1, which actually corresponds to the upper limit of the group’s response capacity.
Figure 4.
Four typical trials of collective response in swarm-robotic experiments. (a) Disordered collective motion with weak alignment weight (wali = 10, αsoc = 0.5) fails to respond to stimuli. (b) Ordered collective motion close to the critical state (wali = 20, αsoc = 0.5) responds rapidly and accurately to stimuli. (c) Ordered collective motion with strong alignment weight (wali = 150, αsoc = 0.5) responds inaccurately to stimuli. (d) Ordered collective motion with strong alignment weight and weak social level (wali = 150, αsoc = 0.2) fails to respond to stimuli. See electronic supplementary material, video S2, for details.
To get a global understanding of collective response under local stimuli, two intuitive metrics, i.e. the group responsiveness (R) and the turning elapsed time (Tturn), are introduced in our study. The group responsiveness R defines the average of acc(t) over time:
| 3.5 |
where tend is the total number of steps in each trial. The turning elapsed time Tturn is defined as the duration it takes for the uninformed robots to perform an efficient collective turning (i.e. acc(t) can converge to close to 1 during a stimulus-changing cycle):
| 3.6 |
where tb and te denote the steps when the informed robot starts to turn and the robotic swarm ends its turn, respectively. Here, te is derived by checking whether the group’s response accuracy acc(t) exceeds a threshold θturn. We set θturn = 0.9 in all trials.
Figure 5 shows the experimental results on collective response to local attractive stimuli. As expected, we observe strong evidence to support the criticality hypothesis. Firstly, as shown in figure 5a1,b1, the group responsiveness R changes non-monotonically as the alignment weight wali and scale Dali increase. R is maximized when wali ≈ 25 and Dali ≈ 40. Secondly, with the same values of wali ≈ 25 and Dali ≈ 40, Tturn is close to the minimum (figure 5a2,b2), while dnn approaches its maximum (figure 5a3,b3). It indicates that the robotic swarm works near the critical state and gets an optimal collective response. Specifically, before the robotic swarm reaches the critical state, R degrades abruptly, and inter-collisions occur frequently (dnn < 80 mm). After the critical state, R gradually decreases as wali and Dali increase. Therefore, we claim that in order to effectively respond to stimuli, the strength (scale) of alignment behaviour between robots cannot be too strong (large) or too weak (small). The optimal collective response occurs near the critical point induced by alignment behaviour, which is in agreement with the criticality hypothesis.
Figure 5.
Experimental results on collective response to local attractive stimuli. (a) Alignment weight wali, (b) alignment scale Dali, (c) noise intensity ηm, (d) social level αsoc. (a1,b1,c1,d1) The group responsiveness R, (a2,b2,c2,d2) the turning elapsed time Tturn and (a3,b3,c3,d3) the minimum nearest neighbour distance 〈dnn〉 as a function of these factors, respectively. 〈dnn〉 is the average of dnn(t) over time. The corresponding time-evolving curves of acc(t), ψ(t) and dnn(t) are presented in electronic supplementary material, figure S3.
The interesting point is that when we turn to the non-alignment factors, there is no evidence to support the criticality hypothesis. As seen in figure 5c1, R falls monotonically as ηm increases. Specifically, when ηm ≤ 0.4, acc successfully converges to approximately 1 (see electronic supplementary material, figure S3c), suggesting that the robotic swarm can respond accurately to local stimuli. Once ηm > 0.4, acc rapidly drops and converges to ∼0 during the stipulated period (data not shown), indicating that the robotic swarm gradually loses its reactivity to stimuli and eventually does not respond at all. Meanwhile, a significant increment of Tturn accompanies the decline in response accuracy (figure 5c2) and a decrease in dnn (figure 5c3), indicating a lag in group turning and more inter-collisions occurring during the process. Thus, in terms of noise increase, the responsiveness of robotic swarms to local perturbations is greatly diminished rather than being enhanced at the disordered–ordered motion transition. In addition, the effect of lowering the social level αsoc on collective response is analogous to that of noise, as seen in figure 5d. In short, when the disordered–ordered motion transition of robotic swarm is induced by noise and social level, the collective response performs the worst, which goes against the criticality hypothesis.
3.3. The functional advantages of alignment-induced criticality are enhanced by non-alignment factors
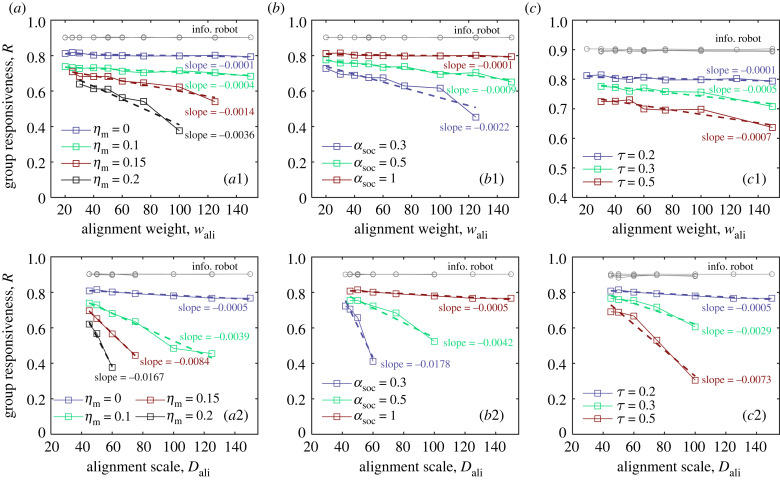
We next turn to investigate the issue of how non-alignment factors impact the collective response of alignment-induced criticality; do they smooth out the peaks near the critical point or make them more pronounced? Figure 6 and electronic supplementary material, figure S4, present the group responsiveness R and the turning elapsed time Tturn as functions of alignment weight and scale for different values of non-alignment factors (i.e. ηm, αsoc and τ). Note that we did not plot the experimental data corresponding to the disordered motion of robotic swarms in these figures.
Figure 6.
Group responsiveness R as a function of alignment weight wali and Dali for different values of (a) noise intensity (ηm = [0, 0.1, 0.15, 0.2]), (b) social level (αsoc = [1, 0.5, 0.3]) and (c) action cycle (τ = [0.2,0.3,0.5]). The dashed lines are fits to a linear dependence of wali (Dali) and R, and their slopes are labelled adjacent to the lines. Note that the data of disordered collective motion are not plotted. The corresponding results of Tturn are presented in electronic supplementary material, figure S4.
In the criticality induced by alignment weight, it can be seen from figure 6a1 that the group responsiveness R decreases with an increase in the noise intensity and is accompanied by a significant extension of the turning elapsed time (see electronic supplementary material, figure S4). Quantitatively, the slope of the fitting line of wali versus R decreases from −0.1 × 10−3 to −3.6 × 10−3 when ηm increases from 0 to 0.2. Similarly, in the criticality induced by alignment scale, figure 6a2 shows that a more significant negative impact is seen on the group responsiveness with an increase in the noise intensity. Correspondingly, the slope of the fitting line of Dali versus R decreases from −0.5 × 10−3 to −16.7 × 10−3 when ηm increases from 0 to 0.2. These results indicate that the advantages of maximizing collective response by alignment-induced criticality become apparent when increasing the motion noise. Also, similar impact can be observed when reducing the social level αsoc or increasing the action cycle τ, as shown in figure 6b1,b2 and figure 6c1,c2, respectively. These results imply that the effect of alignment-induced criticality on collective response is highlighted when the robots behave randomly, less socially, or make lengthy action-decisions.
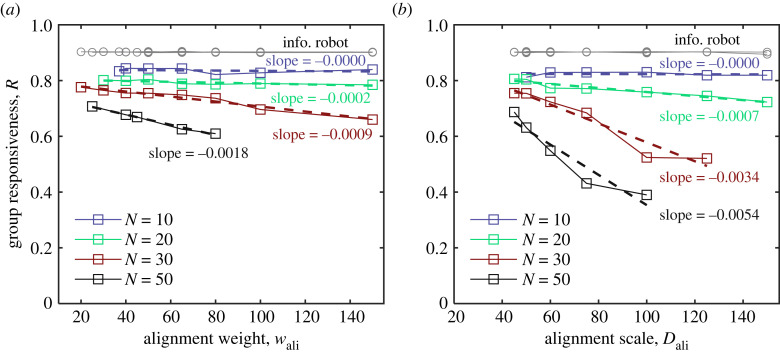
We further explore, to some extent, the influence of group size on the maximization of collective response generated by alignment-induced criticality. Figure 7 and electronic supplementary material, figure S5, show the experimental results with different numbers of robots in relatively small groups (N = [10, 20, 30, 50]). For N = 10, neither R nor Tturn change with the increase of wali and Dali, indicating that the evidence of criticality is not easily noticeable in small-size groups. According to our experimental results, the functional advantages of maximizing collective response arise when the number of robots reaches N = 20 and become apparent when N = 30 and 50. It indicates that the effect of maximizing collective response by criticality gets more pronounced as group size grows, at least for the relatively small groups of robots we considered. Thus, we conjecture that criticality and its impact on group functions may be more evident in large swarm systems. Certainly, more extensive experiments are needed to validate this.
Figure 7.
Group responsiveness R as a function of (a) alignment weight wali and (b) alignment scale Dali for different numbers of robots (N = [10, 20, 30, 50]) with αsoc = 0.5. The corresponding results of Tturn are presented in electronic supplementary material, figure S5. Note that the data of disordered collective motion are not plotted.
3.4. Re-validating the criticality hypothesis using a collective evasion scenario
In this section, we further investigate the functional advantages of alignment-induced criticality in response to more severe and dynamic stimuli. To this end, we consider a predator–prey-like scenario, i.e. the robotic swarm is attacked by a predator, and they have to evade to survive. As seen in figure 1c, we employ a faster robot (vp = 2v0 = 24 mm s−1) as the attacker (predator), which attempts to attack the closest robot. The robots will escape immediately in the opposite direction, with certain motion randomness [53] (ηm = 0.1), when detecting the attacker. To realize the predator–prey scenario with physical robots, we design the attacker’s chasing behaviour and the robots’ escaping behaviour as follows:
| 3.7 |
and
| 3.8 |
where m is the robot closest to the attacker. Desp denotes the maximum distance at which the robot can detect the attacker. is a Heaviside step function.
The informed robot is initially located at the group’s periphery and near the attacker, with a distance between it and the attacker greater than its escape distance, Desp. It acts similarly to the sentry in animal groups, which can detect attackers from a far escape distance (Desp = 1000 mm), while other robots can only detect attackers at relatively short ranges or even not at all (accordingly, in our experiments, Desp = 300 mm and 30 mm are tested). The robotic swarm’s evasion response is quantitatively characterized by the first capture time (Tfc), defined as the time duration from the attacker being seen by the informed robot to it capturing its first target (i.e. a physical touch occurs between them). A larger Tfc indicates that the robotic swarm is more efficient in collective evasion. Like the experiments above, we also use the group polarization ψ and the minimum nearest neighbour distance dnn to quantify the synchronization of robots’ evasive actions and the inter-robot collision risk.
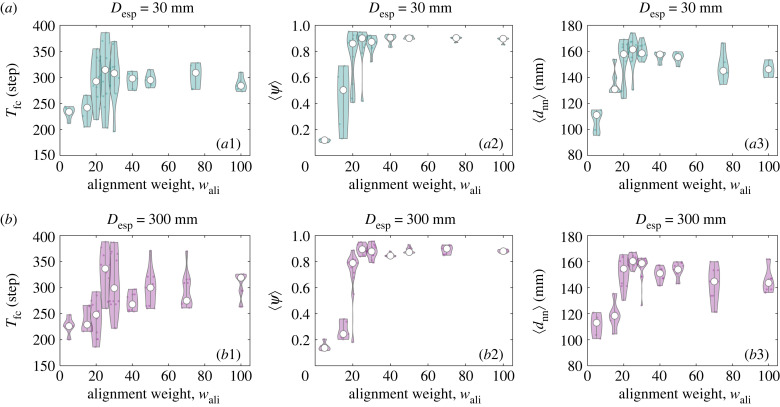
Figure 8 shows Tfc, ψ and dnn as a function of wali with different Desp for prey robots. A peak is seen in each of these metrics near the critical point wali = 25, indicating that at the critical flocking state, the robotic swarm not only has the longest survival time but also has the most synchronized risk-avoidance manoeuvres and the lowest risk of collision among them. In particular, as wali < 25, the robotic swarm moves in a disordered manner, and it cannot avoid attacks by turning collectively, so its survivability is the lowest. While in the case of wali ≥ 25, all robots can turn neatly to avoid threats, but their survivability decreases as the alignment weight increases. Similar to the previous validation, bistability is again observed near the disordered–ordered motion transition point. This result provides evidence that when a robotic swarm works near the critical state, it benefits the survival of group.
Figure 8.
Experimental results on collective evasion. (a) Desp = 30 mm for uninformed robots; (b) Desp = 300 mm for uninformed robots. (a1,b1) The first capture time Tfc, (a2,b2) the group polarization 〈ψ〉 and (a3,b3) the minimum distance of nearest neighbour 〈dnn〉 as a function of alignment weight wali. 〈ψ〉 and 〈dnn〉 are averaged over the first 100 steps and all steps after the attacker was detected, respectively. Initially, robotic swarms are placed face-to-face with the attacker, and the informed robot is located at the very front of the group. In these violin plots, each tiny dot represents a trial data, and the big white point represents the median value of the repeated trials.
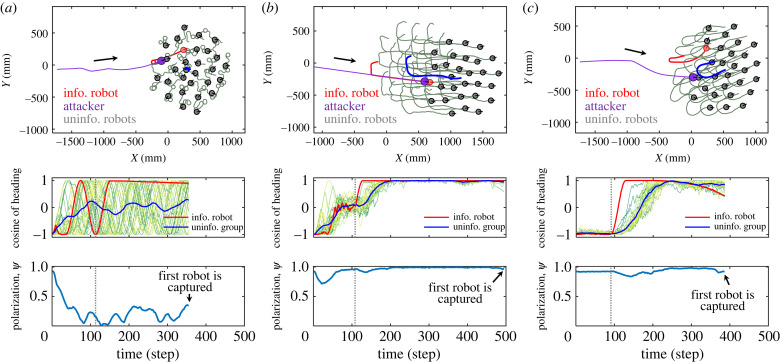
To gain insight into the evasion dynamics of robotic swarms, figure 9 gives three typical trials with wali = 15, 30 and 150, in which the robots’ trajectories, headings, and group polarization are presented. It is seen that robot trajectories are more zigzag-like as wali = 30 than those of wali = 150. However, the escape actions of robots are more organized and coordinated near the critical state, as evidenced by the small fluctuations of headings and the group polarization close to 1 (see electronic supplementary material, figure S6 and video S3, for more information). This is due to the fact that stimuli (i.e. the informed robot’s escape manoeuvre) are transmitted among individuals most efficiently when the robotic swarm is operating near the critical point. In particular, the uninformed robots swiftly ‘copying’ the escape actions of the informed robots for a better evasion efficiency. The experimental results agree with the theoretical prediction of the criticality hypothesis. To sum up, the above experiments validate the criticality hypothesis in terms of its ecological ‘functions’ for groups using this real-life prey–predator scenario.
Figure 9.
Three typical trials of collective evasion in swarm-robotic experiments. (a) The disordered collective motion with weak alignment weight (wali = 15); (b) the ordered collective motion close to the critical state (wali = 30); (c) the ordered collective motion with strong alignment weight (wali = 150). Three rows present robots’ trajectory, profiles of cosine of headings and profiles of polarization, respectively. The grey dashed line indicates the time when the informed robot first detects the attacker. The corresponding snapshots are presented in electronic supplementary material, figure S6; see also video S3 for more information.
4. Discussion and conclusion
Several theoretical hypotheses have been developed over the past century to explain the amazingly large-scale collective responses of bird flocks, fish schools, etc., ranging from the ‘thought transference hypotheses’ [54] to the ‘electromagnetic communication hypotheses’ [55] to the ‘chorus-line hypotheses’ [56]. Recently, using agent-based, bottom-up behavioural models of self-organization, numerous evidences have shown that the large-scale coordinated collective response of animal groups does not need to be interpreted as a phenomenon coordinated by global information or signals but rather by the rapid propagation of local responses about the motion of near neighbours [51,57]. Taking this a step further, criticality, i.e. staying near the edge of transition from disordered to ordered motion, is thought to be a general organizing principle for optimizing animals’ collective behaviours [3,4]. In this study, we established a self-organized robotic swarm system to investigate how criticality shapes group flexibility and functions. By programming the interaction rules of swarm robots, we systematically investigated the spontaneous collective motion, collective response to an attractive stimulus and collective evasion against a predator. Our experimental results provide new evidence for the criticality hypothesis and contribute to clarifying the relationship between different interactional factors and maximization of collective response.
Firstly, we have, for the first time, to the best of our knowledge, validated the functional advantages of alignment-induced criticality in real robotic swarms. Individuals in animal groups strive to align motion direction with their close neighbours, which not only efficiently transmits information between them but also serves to reduce the risk of collisions. Intuitively, when individuals align more strongly with one another, they form a more highly polarized group, which promotes collective sensitivity to weak or ambiguous environmental stimuli. Counterintuitively, our experimental results show that the robotic swarms respond quickly and accurately to weak and dynamic stimuli when individuals align moderately with their neighbours. A higher alignment tendency will hinder the group’s response to environmental stimuli. This result is consistent with previous theoretical results, such as [25,29,43,44,58]. Thus, we suggest setting the alignment strength and its scale as adjustable parameters in theoretical models and investigating their impacts on different collective behaviours, rather than fixing them to specific values, as is widely adopted in the current literature [38,41,58,59]. In this way, some new properties of the self-organized swarm systems may be found or revised.
Secondly, our swarm-robotic experiments confirm that noise (or motion randomness) can induce a disordered–ordered transition in collective motion, but it cannot maximize the collective response of groups. Actually, we show that noise not only suppresses the group’s sensitivity and accuracy in responding to external stimuli but also slows the process of velocity consensus among individuals. Noise is one of the most studied factors of phase transition in swarming systems, and numerous theoretical studies have indicated that it can cause various shifts in group behaviours [38,45]. However, the relationship between noise-induced phase transitions and the efficiency of collective response is not fully understood. Our experimental results show that a certain degree of noise is in favour of the advantages of maximizing collective response by alignment-induced criticality. Due to the pervasive presence of noise in biological systems, we believe that the functional advantages of criticality in real animal groups are more significant than those in noise-free toy models.
Finally, in our swarm-robotic experiments, criticality is achieved by fine-tuning the alignment weight and scale of all robots simultaneously. This is analogous to the way in physics where criticality is obtained by fine-tuning a control parameter, e.g. lowering the temperature to get a gas–liquid or liquid–solid phase transition. However, in many living systems, even without such external tuning mechanisms, entities can reach and stay in a critical state through some internal self-tuning feedback mechanism, known as self-organized criticality (SOC) [2,3]. We argue that the two factors we considered, i.e. social level and action cycle, which are rarely studied in previous models, have the potential to play an essential role in tuning the SOC in animal groups. In our model, the social level characterizes how individuals allocate their attention to integrate personal and neighbours’ motions, which corresponds to animals adjusting their attention to change the strength of coupling with other group mates. The action cycle determines the frequency of individuals executing the ‘perception–action’ loop. It is a temporal scale that characterizes how long it takes for an animal to collect information, make decisions and perform actions in a single cycle. Animals can regulate the frequency of behavioural decisions by the level of tension, and adjust their attention allocation according to scenarios and tasks. Thus, it is plausible to postulate that the level of socialization, action cycle, and even some degree of motion randomness can be used as potential regulators for animal groups to maintain criticality in a self-organized manner. The specific mechanisms of SOC will be the next issue of our investigation in the future.
In conclusion, our swarm-robotic experiments validate that the phenomenon of maximizing collective responses anticipated by the criticality hypothesis does exist in the self-organized swarm systems governed by the Vicsek-like behavioural rules. When the strength and range of alignment behaviours are near the border of transition from disordered to ordered motion, groups obtain the optimal collective sensitivity and adaptation to environmental perturbations. This helps the group to share the sparse route information (group navigation) and escape actions (predator avoidance) efficiently among all members. However, ordered–disordered transitions caused by motion noise, social level and action cycle do not result in any such group-level functional gains, but they act to highlight the advantages of alignment-induced criticality. From a technological perspective, such collective behaviours with criticality provide valuable insights for developing novel solutions for swarm robotics.
Acknowledgements
We thank Shuai Zhang for useful discussions and anonymous reviewers for their insightful feedback.
Appendix A. Swarm robots and experiment set-up
Our SwarmBang robot is a teacup-sized, differential wheel-driven mobile robot (approx. 80 × 80 × 60 mm3); see figure 1a. Each robot is equipped with two stepper motors with wheels, a gimbaled wheel, a set of lithium-ion batteries, and three PCBs stacked together. These PCBs are equipped with a microprocessor and the necessary electronic components, including a PCB for motion control and power management, a PCB for wireless communication and central computing, and one with a monocular camera for visual perception (optional). Moreover, each robot has a top-mounted marker board that holds 4 or 5 passive infrared reflective balls for external localization.
SwarmBang robots move according to specified control commands, i.e. linear speed vc and angular speed ωc. For our behavioural model, vc = v0 and ωc are calculated based on a robot’s desired motion direction . Formally, ωc = min{dθ/τ, ωmax}, where dθ is the angle between the vectors of and , and ωmax is the maximum value of the robot’s angular speed (we set ωmax = 0.4 rad s−1 in experiments). Based on the motion model of two-wheeled differential drive mobile robot, the speeds of left and right wheels are vL = vc − Lωc/2 and vR = vc + Lωc/2, with a wheel spacing of L = 48 mm. To simplify the control, the wheel’s speed is discretized into 25 samples, i.e. vL, vR ∈ {0, 1, 2, …, 24} mm s−1. Thus, we round vL and vR down to integers. Then, the two wheels are driven by stepper motors, that track these speeds in an open-loop fashion.
Our experiments are conducted in an approximately 6.0 m × 6.0 m arena with boundary, see figure 1b, in which a CCD camera (Basler a2A4504-18ucPRO with Kowa LM6FC24M lens) with top-down view is used to record experimental videos. We employ a motion capture system (NOKOV) to track the location and orientation of each robot, from which the robot’s real-time linear speed and angular speed are derived by differential calculation. For the convenience of setting parameters and recording data, our behavioural model runs on a central server computer. The control commands for all robots are packaged into a message and broadcast to the robotic swarm simultaneously with a fixed time interval (i.e. the action cycle τ) using our customized wireless communication protocol. Notably, although our experimental system collects the motion states of all robots centrally and broadcasts their control commands in a centralized manner, the decisions of each robot are made independently based on the local information. Thus, our robots’ behaviour is fully decentralized, autonomous and synchronized.
Data accessibility
The data are provided in electronic supplementary material [60].
Conflict of interest declaration
We declare we have no competing interests.
Authors' contributions
X.L.: conceptualization, investigation, methodology, resources, validation, visualization, writing—original draft, writing—review and editing; Y.X.: data curation, investigation, software, visualization; M.D.: data curation, software, visualization; X.P.: conceptualization, funding acquisition, project administration, resources, supervision, writing—review and editing.
All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Funding
This work was partially supported by the National Natural Science Foundation of China (NSFC) under grant no. 62076203.
References
- 1.Shew WL, Plenz D. 2013. The functional benefits of criticality in the cortex. Neuroscientist 19, 88-100. ( 10.1177/1073858412445487) [DOI] [PubMed] [Google Scholar]
- 2.Roli A, Villani M, Filisetti A, Serra R. 2018. Dynamical criticality: overview and open questions. J. Syst. Sci. Complex. 31, 647-663. ( 10.1007/s11424-017-6117-5) [DOI] [Google Scholar]
- 3.Mora T, Bialek W. 2011. Are biological systems poised at criticality? J. Stat. Phys. 144, 268-302. ( 10.1007/s10955-011-0229-4) [DOI] [Google Scholar]
- 4.Munoz MA. 2018. Colloquium: criticality and dynamical scaling in living systems. Rev. Mod. Phys. 90, 031001. ( 10.1103/RevModPhys.90.031001) [DOI] [Google Scholar]
- 5.Fosque LJ, Williams-García RV, Beggs JM, Ortiz G. 2021. Evidence for quasicritical brain dynamics. Phys. Rev. Lett. 126, 098101. ( 10.1103/PhysRevLett.126.098101) [DOI] [PubMed] [Google Scholar]
- 6.Dahmen D, Grün S, Diesmann M, Helias M. 2019. Second type of criticality in the brain uncovers rich multiple-neuron dynamics. Proc. Natl Acad. Sci. USA 116, 13 051-13 060. ( 10.1073/pnas.1818972116) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Santo SD, Villegas P, Burioni R, Muñoz MA. 2018. Landau–Ginzburg theory of cortex dynamics: scale-free avalanches emerge at the edge of synchronization. Proc. Natl Acad. Sci. USA 115, E1356-E1365. ( 10.1073/pnas.1712989115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mora T, Deny S, Marre O. 2015. Dynamical criticality in the collective activity of a population of retinal neurons. Phys. Rev. Lett. 114, 078105. ( 10.1103/PhysRevLett.114.078105) [DOI] [PubMed] [Google Scholar]
- 9.Daniels BC, Kim H, Moore D, Zhou S, Smith HB, Karas B, Kauffman SA, Walker SI. 2018. Criticality distinguishes the ensemble of biological regulatory networks. Phys. Rev. Lett. 121, 138102. ( 10.1103/PhysRevLett.121.138102) [DOI] [PubMed] [Google Scholar]
- 10.Chen X, Dong X, Be’er A, Swinney HL, Zhang HP. 2012. Scale-invariant correlations in dynamic bacterial clusters. Phys. Rev. Lett. 108, 148101. ( 10.1103/PhysRevLett.108.148101) [DOI] [PubMed] [Google Scholar]
- 11.Palo GD, RG Endres DY. 2017. A critical-like collective state leads to long-range cell communication in dictyostelium discoideum aggregation. PLoS Biol. 15, e1002602. ( 10.1371/journal.pbio.1002602) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gelblum A, Pinkoviezky I, Fonio E, Ghosh A, Gov N, Feinerman O. 2015. Ant groups optimally amplify the effect of transiently informed individuals. Nat. Commun. 6, 7729. ( 10.1038/ncomms8729) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Feinerman O, Pinkoviezky I, Gelblum A, Fonio E, Gov NS. 2018. The physics of cooperative transport in groups of ants. Nat. Phys. 14, 683-693. ( 10.1038/s41567-018-0107-y) [DOI] [Google Scholar]
- 14.Cavagna A, Conti D, Creato C, Del Castello L, Giardina I, Grigera TS, Melillo S, Parisi L, Viale M. 2017. Dynamic scaling in natural swarms. Nat. Phys. 13, 914-918. ( 10.1038/nphys4153) [DOI] [Google Scholar]
- 15.Ginelli F, Peruani F, Pillot M-H, Chaté H, Theraulaz G, Bon R. 2015. Intermittent collective dynamics emerge from conflicting imperatives in sheep herds. Proc. Natl Acad. Sci. USA 112, 12 729-12 734. ( 10.1073/pnas.1503749112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F, Viale M. 2010. Scale-free correlations in starling flocks. Proc. Natl Acad. Sci. USA 107, 11 865-11 870. ( 10.1073/pnas.1005766107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bialek W, Cavagna A, Giardina I, Mora T, Pohl O, Silvestri E, Viale M, Walczak AM. 2014. Social interactions dominate speed control in poising natural flocks near criticality. Proc. Natl Acad. Sci. USA 111, 7212-7217. ( 10.1073/pnas.1324045111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cavagna A, et al. 2022. Marginal speed confinement resolves the conflict between correlation and control in collective behaviour. Nat. Commun. 13, 2315. ( 10.1038/s41467-022-29883-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Makris NC, Ratilal P, Jagannathan S, Gong Z, Andrews M, Bertsatos I, Godø OR, Nero RW, Jech JM. 2009. Critical population density triggers rapid formation of vast oceanic fish shoals. Science 323, 1734-1737. ( 10.1126/science.1169441) [DOI] [PubMed] [Google Scholar]
- 20.Poel W, Daniels BC, Sosna MMG, Twomey CR, Leblanc SP, Couzin ID, Romanczuk P. 2022. Subcritical escape waves in schooling fish. Sci. Adv. 8, eabm6385. ( 10.1126/sciadv.abm6385) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gómez-Nava L, Lange RT, Klamser PP, Lukas J, Arias-Rodriguez L, Bierbach D, Krause J, Sprekeler H, Romanczuk P. 2023. Fish shoals resemble a stochastic excitable system driven by environmental perturbations. Nat. Phys. 19, 663-669. ( 10.1038/s41567-022-01916-1) [DOI] [Google Scholar]
- 22.Tang Q-Y, Hatakeyama TS, Kaneko K. 2020. Functional sensitivity and mutational robustness of proteins. Phys. Rev. Res. 2, 033452. ( 10.1103/PhysRevResearch.2.033452) [DOI] [Google Scholar]
- 23.Moretti P, Muñoz MA. 2013. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 4, 2521. ( 10.1038/ncomms3521) [DOI] [PubMed] [Google Scholar]
- 24.Shriki O, Yellin D. 2016. Optimal information representation and criticality in an adaptive sensory recurrent neuronal network. PLoS Comput. Biol. 12, e1004698. ( 10.1371/journal.pcbi.1004698) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sumpter D, Buhl J, Biro D, Couzin I. 2008. Information transfer in moving animal groups. Theory Biosci. 127, 177-186. ( 10.1007/s12064-008-0040-1) [DOI] [PubMed] [Google Scholar]
- 26.Gautam SH, Hoang TT, McClanahan K, Grady SK, Shew WL. 2015. Maximizing sensory dynamic range by tuning the cortical state to criticality. PLoS Comput. Biol. 11, e1004576. ( 10.1371/journal.pcbi.1004576) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kinouchi O, Copelli M. 2006. Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348-351. ( 10.1038/nphys289) [DOI] [Google Scholar]
- 28.Klamser PP, Romanczuk P. 2021. Collective predator evasion: putting the criticality hypothesis to the test. PLoS Comput. Biol. 17, e1008832. ( 10.1371/journal.pcbi.1008832) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Calovi DS, Lopez U, Schuhmacher P, Chaté H, Sire C, Theraulaz G. 2015. Collective response to perturbations in a data-driven fish school model. J. R. Soc. Interface 12, 20141362. ( 10.1098/rsif.2014.1362) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gollo LL. 2017. Coexistence of critical sensitivity and subcritical specificity can yield optimal population coding. J. R. Soc. Interface 14, 20170207. ( 10.1098/rsif.2017.0207) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vincenzo ID, Giannoccaro I, Carbone G, Grigolini P. 2017. Criticality triggers the emergence of collective intelligence in groups. Phys. Rev. E 96, 022309. ( 10.1103/PhysRevE.96.022309) [DOI] [PubMed] [Google Scholar]
- 32.Hidalgo J, Grilli J, Suweis S, Munoz MA, Banavar JR, Maritan A. 2014. Information-based fitness and the emergence of criticality in living systems. Proc. Natl Acad. Sci. USA 111, 10 095-10 100. ( 10.1073/pnas.1319166111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nonnenmacher M, Behrens C, Berens P, Bethge M, Macke JH. 2017. Signatures of criticality arise from random subsampling in simple population models. PLoS Comput. Biol. 13, e1005718. ( 10.1371/journal.pcbi.1005718) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Priesemann V, Shriki O. 2018. Can a time varying external drive give rise to apparent criticality in neural systems? PLoS Comput. Biol. 14, e1006081. ( 10.1371/journal.pcbi.1006081) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Horsevad N, Kwa HL, Bouffanais R. 2022. Beyond bio-inspired robotics: how multi-robot systems can support research on collective animal behavior. Front. Rob. AI 9, 865414. ( 10.3389/frobt.2022.865414) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lukeman R, L Edelstein-Keshet Y-XL. 2010. Inferring individual rules from collective behavior. Proc. Natl Acad. Sci. USA 107, 12 576-12 580. ( 10.1073/pnas.1001763107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ballerini M, et al. 2008. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232-1237. ( 10.1073/pnas.0711437105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Vicsek T, Czirók A, Ben-Jacob E, Cohen I, Shochet O. 1995. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226. ( 10.1103/PhysRevLett.75.1226) [DOI] [PubMed] [Google Scholar]
- 39.Helbing D, Farkas I, Vicsek T. 2000. Simulating dynamical features of escape panic. Nature 407, 487-490. ( 10.1038/35035023) [DOI] [PubMed] [Google Scholar]
- 40.Inada Y, Kawachi K. 2002. Order and flexibility in the motion of fish schools. J. Theor. Biol. 214, 371-387. ( 10.1006/jtbi.2001.2449) [DOI] [PubMed] [Google Scholar]
- 41.Couzin ID, Krause J, James R, Ruxton GD, Franks NR. 2002. Collective memory and spatial sorting in animal groups. J. Theor. Biol. 218, 1-11. ( 10.1006/jtbi.2002.3065) [DOI] [PubMed] [Google Scholar]
- 42.Couzin ID, Krause J, Franks NR, Levin SA. 2005. Effective leadership and decision-making in animal groups on the move. Nature 433, 513-516. ( 10.1038/nature03236) [DOI] [PubMed] [Google Scholar]
- 43.Kolpas A, Busch M, ID Couzin HL, Petzold L, Moehlis J. 2013. How the spatial position of individuals affects their influence on swarms: a numerical comparison of two popular swarm dynamics models. PLoS ONE 8, e58525. ( 10.1371/journal.pone.0058525) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Couzin I. 2007. Collective minds. Nature 445, 715-715. ( 10.1038/445715a) [DOI] [PubMed] [Google Scholar]
- 45.Van den Broeck C, Parrondo JMR, Toral R. 1994. Noise-induced nonequilibrium phase transition. Phys. Rev. Lett. 73, 3395. ( 10.1103/PhysRevLett.73.3395) [DOI] [PubMed] [Google Scholar]
- 46.Szabó P, Nagy M, Vicsek T. 2009. Transitions in a self-propelled-particles model with coupling of accelerations. Phys. Rev. E 79, 021908. ( 10.1103/PhysRevE.79.021908) [DOI] [PubMed] [Google Scholar]
- 47.Buhl J, Sumpter DJT, Couzin ID, Hale JJ, Despland E, Miller ER, Simpson SJ. 2006. From disorder to order in marching locusts. Science 312, 1402-1406. ( 10.1126/science.1125142) [DOI] [PubMed] [Google Scholar]
- 48.Strömbom D, Hassan T, Greis WH, Antia A. 2019. Asynchrony induces polarization in attraction-based models of collective motion. R. Soc. Open Sci. 6, 190381. ( 10.1098/rsos.190381) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Copenhagen K, Quint DA, Gopinathan A. 2016. Self-organized sorting limits behavioral variability in swarms. Sci. Rep. 6, 31808. ( 10.1038/srep31808) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Reynolds CW. 1987. Flocks, herds and schools: a distributed behavioral model. ACM SIGGRAPH Comput. Graph. 21, 25-34. ( 10.1145/37402.37406) [DOI] [Google Scholar]
- 51.Vicsek T, Zafeiris A. 2012. Collective motion. Phys. Rep. 517, 71-140. ( 10.1016/j.physrep.2012.03.004) [DOI] [Google Scholar]
- 52.Marten S, et al. 2009. Early-warning signals of critical transitions. Nature 461, 53-59. ( 10.1038/nature08227) [DOI] [PubMed] [Google Scholar]
- 53.Domenici P, Blagburn JM, Bacon JP. 2011. Animal escapology II: escape trajectory case studies. J. Exp. Biol. 214, 2474-2494. ( 10.1242/jeb.053801) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Selous E. 1931. Thought-transference (or what!) in birds. London, UK: Constable. [Google Scholar]
- 55.Presman A. 1970. Electromagnetic fields and life. New York, NY: Springer Science + Business Media. [Google Scholar]
- 56.Potts WK. 1984. The chorus-line hypothesis of manoeuvre coordination in avian flocks. Nature 309, 344-345. ( 10.1038/309344a0) [DOI] [Google Scholar]
- 57.Couzin ID, Krause J. 2003. Self-organization and collective behavior in vertebrates. Adv. Study Behav. 32, 10-1016. ( 10.1016/S0065-3454(03)01001-5) [DOI] [Google Scholar]
- 58.Lee S-H, Pak HK, Chon T-S. 2006. Dynamics of prey-flock escaping behavior in response to predator’s attack. J. Theor. Biol. 240, 250-259. ( 10.1016/j.jtbi.2005.09.009) [DOI] [PubMed] [Google Scholar]
- 59.Moussaid M, Garnier S, Theraulaz G, Helbing D. 2009. Collective information processing and pattern formation in swarms, flocks, and crowds. Top. Cogn. Sci. 1, 469-497. ( 10.1111/j.1756-8765.2009.01028.x) [DOI] [PubMed] [Google Scholar]
- 60.Lei X, Xiang Y, Duan M, Peng X. 2023. Exploring the criticality hypothesis using programmable swarm robots with Vicsek-like interactions. Figshare. ( 10.6084/m9.figshare.c.6729995) [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data are provided in electronic supplementary material [60].