Links between breast cancer and birth weight: an empirical test of the hypothesized association between size at birth and premenopausal adult progesterone concentrations

Abstract

Some studies have reported that birth size is a risk factor for breast cancer, but the reasons for this observation are unknown. Ovarian hormone concentrations may be a link between birth size and breast cancer, but the few tests of this hypothesis are inconsistent, perhaps because of differences in sample composition, inclusion of anovulatory cycles, or use of one hormonal measurement per woman. We present results from the first study to use daily hormonal measurements throughout a woman’s complete ovulatory cycle to test the hypothesized relationship between birth size and adult progesterone concentrations. We used a study sample and accompanying data set previously obtained for another research project in which we had collected daily urine samples from 63 healthy premenopausal women throughout a menstrual cycle. Multivariate regression was used to test for trends of individual progesterone indices (from 55 ovulatory cycles) with birth weight or ponderal index, while controlling for age, adult BMI, and age at menarche. Our main finding was that neither birth weight nor ponderal index was associated with biologically significant variation in luteal progesterone indices; the best-estimated effect sizes of birth size on these progesterone indices were small (3.7–10.2 %). BMI was the only significant predictor of mean peak urinary progesterone, but it explained <6 % of the variance. Our findings, in light of what is currently known regarding associations of breast cancer risk with birth size and adult size, suggest that environmental factors (particularly those that vary by socioeconomic status and affect growth) may underlie associations between birth size and cancer risks without there being any association of birth size with adult ovarian hormone concentrations.

Background

Several studies have reported a positive association between a woman’s birth weight and her risk of breast cancer later in life [1–9]. Although the specific reasons for this association remain unknown, ovarian hormones (estrogens and progesterone) are thought likely to be involved because of their proliferative effect on cell division in breast tissue [10], and the finding that concentrations of some (though not all) ovarian hormones are risk factors for breast cancer ([11] and references therein). It has therefore been expected that birth weight would be predictive of adult ovarian hormone concentrations [12].

Results from the few published tests of this latter hypothesis are inconsistent, perhaps because of study differences in sample composition and analytical approaches. For example, adult salivary estradiol concentrations were positively associated with ponderal index (PI, birth weight/birth length³) at birth in Polish women [13, 14], but these samples included individuals of very low birth weight (defined as <1500 g) [15] and/or who had been small for gestational age (defined as a PI of <20 kg/m³) [16] and therefore may have had developmental problems that could have confounded the analyses. In a sample of Norwegian women of normal birth weights, salivary estradiol concentration was negatively associated with birth weight [17], contrary to what would be expected if breast cancer risk rises with increasing estrogen concentrations. Tworoger et al. [18] found no relationships between birth weight and follicular or luteal estrogens or progesterone concentrations in participants in the Nurses’ Health Study II in the USA. But this study relied on only a single measurement of hormones during each cycle phase which, as the authors noted, may have been an inadequate proxy for total hormone production because of the high day-to-day variability in hormone concentrations during a single ovarian cycle for a given woman [19, 20].

An adequate evaluation of the relationship between hypothesized predictor variables and ovarian steroid concentrations in premenopausal women requires studies using frequent hormone measurements throughout the menstrual cycle [21, 22]. Although adult body size is positively associated with ovarian steroid concentrations [22], the putative relationship between birth weight and adult progesterone concentrations has yet to be evaluated with an estimate of total hormone production that is based on multiple measurements made during the entire luteal phase. To the best of our knowledge, the study presented here is the first to address this need.

Using a study sample and accompanying data set previously obtained for another research project, we tested the hypothesis that birth size is predictive of adult progesterone concentration using daily urinary hormone measurements throughout a complete ovulatory cycle from each study participant. Although data were not available for other hormones, and the sample size was modest, the very high sampling density yields both a more accurate estimate of total progesterone production during the entire luteal phase and better identification of anovulatory cycles. Study participants met strict exclusion criteria for health and birth weight.

A positive association between birth weight and indices of luteal-phase progesterone concentration in our study sample would tend to support the arguments that birth weight is a marker of processes that influence adult ovarian steroid concentrations and breast cancer risk. Alternatively, absence of an association would be consistent with the findings of Yang et al. [23] who recently reported that although adult height and birth weight are highly correlated, adult height but not birth weight was associated with breast cancer risk in a large UK cohort study that had controlled for a number of known risk factors but which had not included any hormonal measurements.

Methods

Study sample and data collection

All study protocols were approved by the Institutional Review Board at Indiana University, and all participants gave written informed consent. Healthy participants (n = 63) were recruited from Leipzig, Göttingen, Potsdam, and Hannover, Germany, during 2008 through posted notices and by word of mouth. These women were premenopausal, had not used hormonal contraception for at least 3 months prior to study, had never had any hormonal medical treatments, were not following any special dietary practices or physical training regimens, and were not trying to become pregnant. All women had been full-term babies with a birth weight of at least 2350 g.

For each participant, body weight and height were measured, measurements at birth were copied from written records, and reproductive history was recorded during a private interview at the laboratory. Women were instructed in sample collection and record keeping and given the necessary materials. Daily urine collection began the first morning after vaginal bleeding started and continued through at least the first day of vaginal bleeding of the subsequent cycle. First morning urine was self-collected, pipetted into polypropylene 2-ml cryovials, and stored frozen (≤−5 °C) at home until the completion of sampling, at which time the box of samples was transported in an insulated box with ice packs to the laboratory where they were stored at −20 °C until assayed.

Hormone assays

Urine samples were assayed for pregnanediol glucuronide (PdG), the principal urinary metabolite of progesterone. We measured immunoreactive PdG in urine samples with a direct microtiter plate enzyme immunoassay using the streptavidin-biotin technique [24]. We used an antiserum raised in a rabbit against pregnanediol-3-glucuronide-BSA and biotinylated PdG as a label as previously described in detail by Heistermann et al. [25]. With PdG as a standard (100 %), the antibody showed the following cross-reactivities: 20α-hydroxyprogesterone 32 %, pregnanediol 22 %, 5α-pregnane-20α-ol-3-one 14 %, progesterone 0.5 %, and <0.1 % for all other steroids tested (including cortisol). Inter-assay coefficients of variation were 11.7 and 11.4 % for high- and low-value quality controls respectively. Intra-assay coefficients of variation were 10.1 and 7.8 % for high- and low-value quality controls respectively. PdG concentrations standardized by either creatinine [Cr] or specific gravity gave qualitatively comparable results in our statistical analyses; therefore, only analyses of Cr-standardized measurements (expressed as ng PdG/mg Cr) are presented here.

Analyses

For each woman’s cycle, serial Cr-standardized PdG values were aligned on the first day of the subsequent cycle (=day₀). The timing of ovulation was determined by a sustained rise in PdG of 2 standard deviations above the mean of the previous three to five values (following Deschner et al. [26]). PdG indices were defined as (∫ of PdG from day_x to day_y)/(day_y − day_x), where x to y is any span of days and PdG at any time is defined by linear interpolation of the observed PdG measurements [27,28]. Defined indices in our analyses were mean-luteal-PdG (x = day of ovulation − 0.5, y = −0.5), mean-peak-PdG (x = day of peak luteal PdG − 2.5, y = day of peak luteal PdG + 2.5) and mean-follicular-PdG (x = first observation + 2, y = day of ovulation − 1.5). Cycles in which (mean-luteal-PdG) < 2(mean-follicular-PdG) were designated anovulatory and excluded (n = 5), as were 2 cycles of unusual length (>47 days). Birth weight was missing for 1 woman. The final analytical sample comprised 55 women, each with 1 complete ovulatory cycle. Table 1 presents descriptive statistics for this analytical sample.

Table 1.

Descriptive statistics for predictor and outcome variables

	Min	Max	Mean	Median	Std. dev
Birth weight (grams)	2350	4300	3300	3320	447
Birth ponderal index (kg/m3)	15.4	31.3	25.2	25.6	3.1
Age at time of study (years)	22.3	40.6	29.9	29.0	4.9
Adult height (cm)	155.3	176.1	167.0	167.0	5.1
Adult weight (kg)	48.4	87.0	63.0	63.6	8.2
Adult BMI (kg/m2)	19.0	28.3	22.5	22.0	2.4
Age at menarche (years)	9.9	17.5	13.4	13.3	1.5
Mean-peak-PdG (ng PdG/mg Cr)	1500	9928	4966	4948	1872

Ponderal index was calculated from size [m] and weight [kg] at birth using the formula PI = weight_[kg]/size_[m] ³. Ponderal index, also called Rohrer’s index, has been used as an indicator for “fatness” or “thinness” in newborns and infants because, unlike body mass index (weight/height²), it is independent of height and age in the study population [29,30]. It has been shown that ponderal index provides a valuable and meaningful parameter for assessing fetal condition and nutrition in newborn infants [31–33].

Multivariate linear regression was used to test for trends of both luteal PdG indices with size at birth (birth weight and PI), while controlling for the potential confounders age, BMI, and age at menarche (some similar prior studies have used stepwise linear regression, but we did not because of problems with that approach; see Mundry and Nunn [34]). Analyses were done with SPSS (v. 21); significance was set at p ≤ 0.05. Variables were checked for normality with the Shapiro-Wilk test. Those variables not normally distributed were transformed (BMI = 1/x ², age = 1/x ², and PI = x ³) to meet this assumption of linear regression. Each independent variable was then centered at its sample mean. To mitigate the risk of spurious associations (see Holländer et al. [35] and additional discussion below), our statistical analyses did not presume arbitrarily selected bins (thresholds, cutoffs) for any continuous predictor (independent) variables.

Results

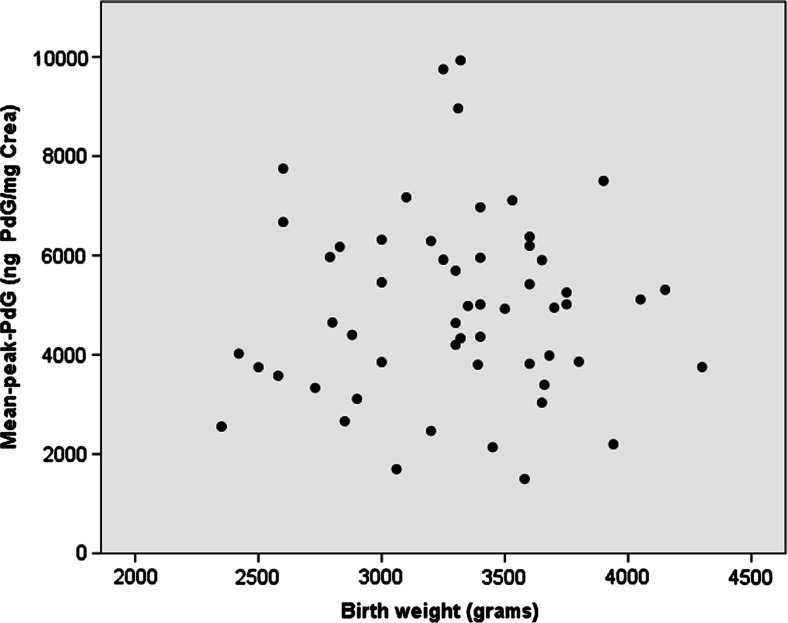
Table 2 presents results of the four regression models (mean-peak-PdG regressed on either birth weight or PI³, and mean-luteal-PdG regressed on either birth weight or PI³). Mean-peak-PdG was not associated with birth weight (model 1A: F _(4,50) = 1.158, p = 0.341, R ² = 0.085, Fig. 1) or PI³ (model 1B: F _(4,50) = 1.258, p = 0.299, R ² = 0.091). Similarly, mean-luteal-PdG was not associated with birth weight (model 2A: F _(4,50) = 0.746, p = 0.565, R ² = 0.056) or PI³ (model 2B: F _(4,50) = 0.842, p = 0.505, R ² = 0.063). Each of these models explained <10 % of the variance in the PdG index. The best-estimated effect sizes of birth size on PdG indices were also small (standardized β = 0.061, −0.102, 0.037, and −0.091 for models 1A, 1B, 2A, and 2B respectively, i.e., for example, in model 1A, a 1-standard-deviation change in birth weight was associated with only a 0.061-standard-deviation increase in mean-peak-PdG).

Table 2.

Multivariate models of progesterone indices

		Predictor variables	p value	t value	Unstandardized coefficients		95 % confidence intervals		Standardized coefficients
					b	Std. error	Lower limit	Upper limit	β	Std. error
(Model 1A) Response variable 1: mean-peak-PdG (ng PdG/mg Cr)		Birth weight (g)	0.659	0.444	0.255	0.575	−0.900	1.411	0.061	0.138
		1/age2	0.868	−0.168	−121,000	723,000	−1,570,000	1,330,000	−0.023	0.137
		1/BMI2	0.045	2.055	1,400,000	683,000	31,900	2,780,000	0.306	0.149
		Age at menarche	0.618	−0.502	−93.2	186	−466	279	−0.074	0.147
(Model 1B) Response variable 1: mean-peak-PdG (ng PdG/mg Cr)		Ponderal index3	0.457	−0.750	−0.034	0.046	−0.127	0.058	−0.102	0.138
		1/age2	0.909	−0.114	−82,600	723,000	−1,530,000	1,370,000	−0.016	0.140
		1/BMI2	0.047	2.033	1,380,000	677,000	16,800	2,740,000	0.300	0.148
		Age at menarche	0.567	−0.576	−106	184	−476	264	−0.084	0.146
(Model 2A) Response variable 2: mean-luteal-PdG (ng PdG/mg Cr)		Birth weight (g)	0.793	0.264	0.100	0.381	−0.665	0.865	0.037	0.141
		1/age2	0.772	−0.291	−139,000	479,000	−1,100,000	822,000	−0.041	0.141
		1/BMI2	0.113	1.614	730,000	452,000	−178,000	1,640,000	0.244	0.151
		Age at menarche	0.648	−0.460	−56.5	123	−303	190	−0.068	0.148
(Model 2B) Response variable 2: mean-luteal-PdG (ng PdG/mg Cr)		Ponderal index3	0.513	−0.659	−0.020	0.030	−0.081	0.041	−0.091	0.136
		1/age2	0.810	−0.242	−116,000	478,000	−1,080,000	845,000	−0.034	0.141
		1/BMI2	0.114	1.607	720,000	448,000	−180,000	1,620,000	0.241	0.150
		Age at menarche	0.610	−0.514	−62.7	122	−308	182	−0.076	0.148

Fig. 1.

Scatterplot of mean-peak-PdG and birth weight. Each dot represents one of the research subjects and is plotted according to their birth weight on the x-axis and their mean-peak-PdG on the y-axis

The only significant predictor variable was 1/BMI² in models 1A and 1B: as BMI increased (hence 1/BMI² decreased), mean-peak-PdG decreased. The effect sizes for 1/BMI² in the four models were all very similar (standardized β ranging from 0.241 to 0.306). For mean-peak-PdG, these effects just reached significance (p = 0.045 and 0.047 for models 1A and 1B respectively), while for mean-luteal-PdG, these effects were not significant. However, 1/BMI² explained less than 6 % of the variance in mean-peak-PdG. In other words, these effects, while statistically significant, are biologically minor. For all the other predictor variables (confounders), the best-estimated effect sizes were small (standardized β < ∼0.1 in magnitude) and non-significant.

Discussion

Our main result was that neither birth weight nor ponderal index was associated with biologically significant variation in either of our luteal progesterone indices. That is, these data and analyses do not support the hypothesis of an association between birth size and progesterone concentration in premenopausal women. Our findings, based on daily measurements of urinary PdG throughout an ovulatory cycle, confirm those of Tworoger et al. [18], which were based on only a single luteal-phase measurement of serum progesterone, and are also consistent with Yang et al. [23], who found that birth weight alone was not associated with breast cancer risk in a large UK sample.

Unlike previous studies, we did not divide continuous variables into discrete categories for analysis. Holländer et al. [35] argue that binning (i.e., dividing a continuous variable into discrete categories based on, for example, percentiles) can make cross-study comparisons difficult because the cutoff points cannot be replicated across different studies. Furthermore, creating categories assumes a flat relationship between predictor and response variables within categories and a discontinuity in the response as boundaries between intervals are crossed [36]. Because different cutoffs can produce different results and multiple interpretations of the same data, studies are susceptible to arbitrary and manipulative data processing [37,38]. For these reasons, we did not bin our data.

In addition, we excluded anovulatory cycles from our analyses because these cycles lack a post-ovulatory rise in progesterone (which in ovulatory cycles is produced by the corpus luteum that develops from the ruptured follicle after ovulation). Without ovulation, there is no luteal phase (i.e., “luteal-phase progesterone concentration” is not a biologically meaningful measurement for an anovulatory cycle). The inclusion of anovulatory cycles in analyses biases the sample-mean progesterone concentration downwards by an amount which (depending on the fraction of these cycles in the sample) varies from one study sample to another. For example, exclusion of anovulatory cycles increased the sample’s mean peak-progesterone index by 58 % in a sample of poorer Bolivian women but had little effect on hormone indices in samples of better-off Bolivian or Chicago women, in whom anovulatory cycles were much rarer [27]. Inclusion of anovulatory cycles would have given the impression that luteal-phase progesterone was dramatically lower in the poorer Bolivians, but in fact, the anovulatory rate was much higher and luteal-phase progesterone was only modestly (but nonetheless, significantly) lower than that of the better-off Bolivians [27]. Therefore, because inclusion of anovulatory cycles introduces a non-random source of inter-individual and inter-sample hormonal variation that can result in erroneous conclusions about the associations of hormone concentrations with other variables, we excluded all anovulatory cycles from our regression analyses.

Our study only included healthy women who were full-term healthy newborns. Low birth weight and preterm birth are associated with a variety of adult pathologies [39–41] that could confound analyses of hypothesized associations between birth size and adult hormone concentrations. For example, the study samples of Polish women [13,14] included women who had had very low birth weights and/or low PIs (indicative of being small for gestational age). In one analysis, the first birth weight quartile of that study sample is 1300–3000 g with a mean of 2599 g, indicating that a significant portion of the infants in this quartile were low birth weight (<2500 g) or very low birth weight (<1500 g) [15]. Similarly, the low PI tertiles in both analytical samples [13,14] each had average PIs (17.7 and 18.1 kg/m³ respectively) below the usual threshold (20 kg/m³) for considering a newborn to be small for gestational age [16]. In one of several analyses, they found that women in the lowest birth weight quartile had lower estradiol than women from the other three quartiles [13]. This observation may be informative about the links between early life pathology and adult dysfunction [39–41], but it does not address whether increasing birth weight within a population of normal weight healthy newborns is positively associated with higher adult ovarian hormones.

In our study, we found a positive relationship between 1/BMI² and PdG (indicating a negative association between BMI and urinary progesterone concentrations) in premenopausal women, but this variable explained <6 % of the variance of mean-peak-PdG. Other studies of premenopausal women have also found inverse associations between reproductive hormone concentrations and BMI [11,18,42]. Potischman et al. [42] reported a trend towards lower concentrations of estradiol associated with increasing BMI among premenopausal women, but this was not significant (p = 0.11); Tworoger et al. [18] found adult BMI was inversely associated with total estradiol concentrations (p < 0.001).

In sum, there have been inconsistent findings on the relationships between birth weight, hormones, and breast cancer. As reviewed by Hankinson and Eliassen [21], many studies have reported a positive association between birth weight and breast cancer risk [1–9], but others have failed to find a significant relationship [23,43–45]. It has been argued that reproductive hormones may be one mechanism underlying an association between birth weight and breast cancer. However, published tests of this hypothesis are at odds, perhaps because of methodological features that are better avoided in future studies. Notably, women born prematurely or of low or very low birth weight should be treated as separate samples or as outliers, and should not be included in samples of women who were full-term healthy newborns. Frequent sampling of biomarkers throughout the ovulatory cycle should be used to assess hormone concentrations and to evaluate the occurrence and timing of ovulation. Anovulatory cycles should be detected and treated as a distinct subsample (to be excluded in most analyses). Binning continuous variables should be avoided, as it introduces an element of arbitrariness into statistical analysis [35–38] and reduces statistical power.

It remains unknown whether or not birth weight is in fact a marker of processes that themselves affect adult breast cancer risks. Having controlled for adult height, Yang et al. [23] reported no association between birth weight and adult breast cancer risk. However, they did find strong and highly significant (p < 0.0001) associations between adult height and breast cancer risk, and argued that environmental determinants of growth may be important in understanding adult cancer risk.

Collectively, the results from Tworoger et al. [18], Yang et al. [23], and our study suggest that adult progesterone concentrations do not underlie any reported associations between birth weight and breast cancer risk. Birth weight is amply demonstrated to be positively associated with various socioeconomic variables [46]. Breast cancer risk and survival [47–49] and adult ovarian hormone concentrations [27] are also associated with markers of socioeconomic conditions, but these are not necessarily the same socioeconomic variables that are associated with birth weight. Thus, environmental factors, particularly those that vary by socioeconomic status and affect growth, may underlie the apparent positive associations between birth weight and cancer risks observed in some, but not all, studies without there being any substantial association of birth weight with adult ovarian hormone concentrations.