Figure 1. The structure-resolved reaction-diffusion model for Gag assembly on spherical membranes.

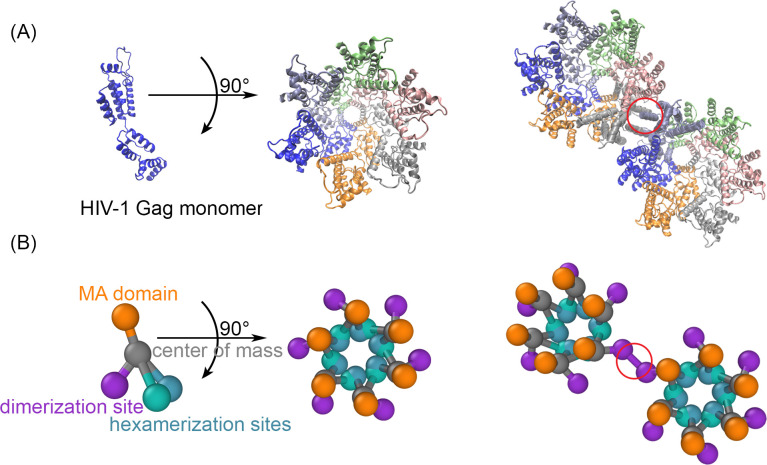
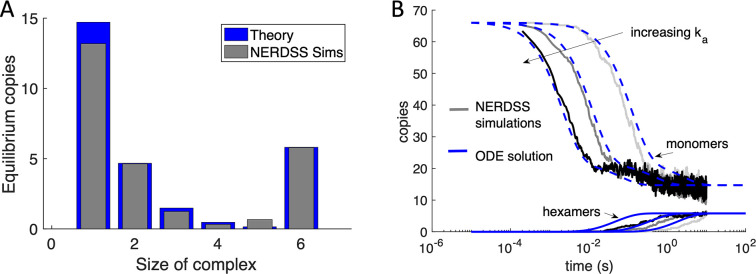
(A) The Gag monomers from the cryoET structure of the immature lattice (Schur et al., 2016) taken from 5L93.pdb is shown on its own, as part of a single hexamer (center), and with a dimerization interface in the red circle that brings together two hexamers (right). (B) Our coarse-grained model is derived from this structure to place interfaces on each monomer at the position where they bind. The reaction network contains three types of interactions. The MA domain (orange) binds to the membrane. The position of the MA site is not in the cryoET structure, and we position it to place each monomer normal to the surface. The distance of the MA site from the center of mass is set to 2 nm. The hexamerization sites (green and blue) mediate the front-to-back binding between monomers to form a cycle. The dimerization site (purple) forms a homo-dimer between two Gag monomers, as illustrated on the right. The reactive sites are point particles that exclude volume only with their reactive partners at the distances shown. Thus, the hexamer-hexamer binding radius is 0.42 nm, whereas the longer dimer-dimer binding radius is 2.21 nm. Positions and orientations are defined in Source Data. The experimental lattice has an intrinsic curvature, and our model recapitulates this to assemble a sphere. The binding kinetics between the interaction types for multiple rates was validated against theory (Figure 1—figure supplements 1 and 2), and we verified that the lipid binding site model did not significantly impact the dynamics of the lattice (Figure 1—figure supplement 3). The positioning of the Gag interfaces in this model of the immature lattice are distinct from a model that would assemble the mature lattice (Figure 1—figure supplement 4).

Figure 1—figure supplement 1. Kinetics of dimer formation between Gag monomers is consistent with theory.

In these simulations, only the homo-dimer contacts could form, and the hexamer sites were turned off. Thus, the kinetics of reversible dimerization from NERDSS simulations (colored lines) can be compared with the non-spatial rate-equation solution (black dashed). Here, we initialized all monomers to be on the membrane surface irreversibly, so the binding is purely in 2D. For each model, 5–10 trajectories were collected and averaged. As the microscopic association rate k_a was increased, we also increased the dissociation rate k_b the same amount, so that the free energy was fixed for all simulations at –11.9k_BT. The apparent 3D rates for the slowest system were k_a^3D=0.025 nm³/μs and k_b = 0.1 s^–1. The length-scale to convert from 3D rates to 2D rates was set here to h=5 nm, hence the slowest 2D rate is k_a^2D=0.005 nm²/μs. Initial copy numbers were 66 on the same membrane sphere with R=67 nm. D=0.2 nm²/μs and σ=2.21 nm. For the analytical solution in black dashed, we input the corresponding macroscopic 2D rates k_on^2D and k_off^2D. The macroscopic on-rate k_on^2D≤ k_a^2D due to its dependence on diffusion constants and the system size. We note that the agreement is not perfect between the reaction-diffusion simulations and the non-spatial solution. Although the kinetics are not expected to be identical in 2D due to sensitivity to spatial fluctuations, there is some disagreement because in the RD simulations, some of the association events were rejected if the monomers were not aligned closely enough to their target bound state, which causes a relative slow-down in the association rates. Specifically, we found that the rates that we assigned via the input files, for instance k_a^2D=0.02 nm²/μs, when simulated, produced kinetics with an apparent rate that was 4× slower. This same factor of 4 slow-down was observed for input rates of 0.2 and 2 nm²/μs. The dissociation kinetics are unaffected. We reject association events that cause a reorientation of the monomers into the bound state that is larger than our specified threshold. Our threshold is controlled by a scale-factor (scaleMaxDisplace) that was set low enough (to 10) for the slowly diffusing and non-rotating 2D monomers that events were rejected. We therefore report throughout the paper the rates that describe the actual observed kinetics and are thus 4× lower than the values we specified in our input files. We performed the same validation for the Gag monomers to form hexamers, with the dimer interaction turned off but still excluding volume. Here, again we found the same 4× slow-down in association kinetics relative to the assigned rates in the input file. Therefore, we always report these apparent rates that accurately describe the kinetics.

Figure 1—figure supplement 2. NERDSS simulations of purely hexamer assembly in 2D are validated against theory.

(A) Here, the Gag monomers could only bind through their hexamer sites, and the dimer sites were turned off (but could still exclude volume). With 66 initial Gag monomer copies initialized irreversibly on the spherical surface, the monomers could assemble into complexes from dimers up through to completed hexamers purely in 2D. The equilibrium yield here calculated numerically (blue bars) which agrees very well with the simulated equilibrium (gray bars). The free energy is ∆G_hex = −8.93k_BT. When the hexamer loop closes, the strength of the final two bonds is slightly less than 2∆G_hex, and instead is 2∆G_hex+2.3k_BT. We introduce this small penalty to mimic that the hexamer structure is not ideal. (B) We compare the kinetics of assembly from the NERDSS simulations (gray solid lines) with a set of non-spatial ordinary differential equations (ODEs) for hexamer formation solved numerically in MATLAB. The monomer population decreases from 66 copies (upper curves), while the hexamers assemble to their equilibrium value of ~6 (lower curves). The free energy for all simulations is the same as described in (A), and the microscopic rates increase from right to left as k_a^3D=0.025, 0.25, and 2.5 nm³/μs, with the length-scale from 3D to 2D set at the same value used in the full system as h=10 nm. The microscopic dissociation rates thus also increase accordingly from 2 to 200 s^–1. Diffusion D=0.2 nm²/μs for each membrane-bound monomer, and the binding radius for the hexamer interaction is σ=0.418 nm The agreement between the NERDSS simulations and the ODEs are relatively strong, although the simulated hexamers assemble more slowly. This is in large part due to the excluded volume of the monomers (via their dimer sites) that slows the collisions between the reactive hexamer sites.

Figure 1—figure supplement 3. Comparison of the dynamics of remodeling simulations using the implicit lipid model and explicit lipids.

(A) Time dependence of the size of the largest assembled complex during the simulation. (B) Time dependence of the number of fragments in the system. A fragment is a complex with at least 30 Gags. ${\displaystyle \mathrm{\Delta }{G}_{\mathrm{h}\mathrm{e}\mathrm{x}}=-5.62k_{\mathrm{B}}T}$ and k_a^2D (nm²/μs)=2.5 × 10^–2 for both implicit and explicit simulations. Overall the agreement is very close, with small deviations between the equilibrated number of fragments for this unstable system, likely due to the assumption in the implicit lipid model that the lipids are well mixed, which could speed up rebinding times. The proteins still remain affixed to the 2D membrane surface with explicit or implicit lipid sites.

Figure 1—figure supplement 4. Comparison of the coarse-grained model of Gag monomer from the immature and mature lattice.

(A) The cartoon representation shows the experimental HIV-1 immature lattice structure from 5L93.pdb with 18 Gag monomers. To determine the position of the interaction sites between adjacent Gag monomers for the coarse-grained model, we calculated the average positions of all the atoms within a cutoff distance 0.35 nm from adjacent Gag monomers. The resulting interaction sites are represented with beads. Gray beads are the centers-of-mass (COM) of one Gag monomer. Cyan and light blue beads indicate the hexamerization sites, and magenta beads show the homo-dimerization sites between hexamers. The orange beads are the membrane binding sites, which are not included in the experimental structure but placed manually 2 nm above the COM in the direction normal to the membrane surface. A coarse-grained Gag monomer is depicted below the 18 Gag monomers complex. (B) The experimental HIV-1 mature capsid structure (3J34.pdb) and the coarse-grained model derived using the same method as in the determination of model for the immature lattice. A coarse-grained Gag monomer is illustrated below the 42 Gag monomers complex for the mature lattice system.